Similar presentations:
Нормализация (Нормальные Формы высших порядков)
1. Нормализация (Нормальные Формы высших порядков)
Бессарабов Н.В.bes@fpm.kubsu.ru
2018 г.
1
2. Цели лекции
В этой лекции завершим рассмотрение процессов нормализации.Рассмотрим оставшиеся четвёртую, пятую нормальные формы и
нормальную форму домен-ключ.
К определению четвёртой нормальной формы придем через
обобщение понятия функции, заданной на отношении, до многозначной
функциональной зависимости. Обобщение теоремы Хиса на такие
зависимости называется теоремой Фейгина. Она определяет правило
приведения к четвертой нормальной форме.
Бегло рассмотрим дальнейшее обобщение понятия функции
до зависимости проекция-соединение. На его основе определим
пятую нормальную форму и правила приведения к ней.
Рассмотрим определение нормальной формы домен-ключ,
играющей важную роль в теории и ограничивающую дальнейшие
поиски нормальных форм.
И в самом конце мы обнаружим, что после нормализации
разработчик может денормализовать некоторые отношения.
Бессарабов Н.В.2018
2
3. Многозначные зависимости. Пример 1.
Особенность:Все учебники обязательны для всех лекторов,читающих курсН1НФ
Дисциплина
Арифметика
Генетика
Лектор
Иванов
Петров
Карпов
Учебник
Чучкин/Пупкин
Малинин/Буренин
Вайсман
Лысенко
1НФ
Дисциплина
Арифметика
Арифметика
Арифметика
Арифметика
Генетика
Генетика
Лектор
Иванов
Иванов
Петров
Петров
Карпов
Карпов
Учебник
Малинин/Буренин
Чучкин/Пупкин
Малинин/Буренин
Чучкин/Пупкин
Вайсман
Лысенко
PK
PK
Лектор и учебник независимы в том смысле, что возможны любые
сочетания их значений. С одной стороны получена НФБК, так как имеется
единственный ключ и возможны только тривиальные зависимости. С
другой стороны налицо избыточность. Имеются аномалии по включению
(одного лектора включаем 2 раза) и т.д.
Замечание: Обратите внимание, что в 1НФ ключ образуется двумя
независимыми столбцами.
3
4. Многозначные зависимости.
Многозначные зависимости (multi-valued dependency) возникаюткогда необходимо привести к первой нормальной форме отношение,
с независимыми многозначными атрибутами. Пусть имеется два таких
атрибута Y и Z. Тогда для получения 1НФ необходимо для каждого
набора значений остальных атрибутов X повторить эту строку для
каждого сочетания атомарного значения Y с каждым атомарным
значением Z. Как Вы помните, это называется выравниванием таблицы.
Образуется многозначная зависимость в которой:
• каждому значению X соответствует набор значений Y;
• каждому значению X соответствует набор значений Z;
• значения атрибутов Y и Z не зависят один от другого.
Многозначную зависимость принято обозначать X Y|Z, хотя
можно было бы указать наличие двух существующих одновременно
обычных функциональных зависимостей X Y и X Z.
Иногда обозначают многозначную зависимость X Y или X Z.
Определение: MV-зависимость X Y называется тривиальной если
X Y, либо X U Y = {X,Y,Z}.
Бессарабов Н.В.2018
4
5. Определение MV-зависимости
Определение: Пусть r – отношение со схемой R(S), а X,Y,Z -непересекающиеся множества его атрибутов, такие, чтоX Y Z=S. Атрибуты Y и Z многозначно зависят от X
(обозначение X Y|Z) если из того, что в отношении r
содержатся кортежи
r1 = (x, y, z1) и r2 = (x, y1, z) следует, что в отношении r
содержится также кортеж r3 = (x, y, z).
Замечание 1: По симметрии определения в r содержится
и кортеж r4 = (x, y1, z1). Атрибуты Y и Z как бы симметричны
по отношению к X.
Замечание 2: При наличии MV-зависимости кортежи
обязаны вставляться и удаляться одновременно целыми
наборами.
Бессарабов Н.В.2018
5
6. Теорема Фейгина (R. Fagin)
Теорема Фейгина: Пусть X, Y, Z три непересекающиеся подмножестваатрибутов отношения r со схемой R(X,Y,Z ). Декомпозиция отношения r
на проекции {X,Y} и {X,Z} будет декомпозицией без потерь тогда и
только тогда, когда имеется многозначная зависимость X Y|Z.
Частный случай тривиальной MV-зависимости: Если зависимость
X Y|Z является тривиальной, т.е. существует только одна из
функциональных зависимостей X Y или X Z, но не может быть
задана независимость Y и Z, то получаем теорему Хиса.
Определение 4НФ: Отношение находится в четвёртой нормальной
форме если оно находится в нормальной форме Бойса-Кодда и не
содержит нетривиальных многозначных зависимостей.
Теорема Фейгина обобщает теорему Хиса
на многозначные функциональные зависимости
Бессарабов Н.В.2018
6
7. Использование теоремы Фейгина
Пояснение 1: Теорема Фейгина дает правило приведения кчетвертой нормальной форме (4НФ).
Пояснение 2: Отношения с нетривиальными многозначными
зависимостями могут появиться при хранении в одном
отношении двух независимых сущностей. Такое отношение
образуется как естественное соединение двух отношений по
общему полю, которое не образует полного ключа ни в одном
из этих отношений.
Пример: Объединение двух отношений
“Работник- Должность” (допускается совместительство) и
“Работник – Ребенок” вызывает появление многозначной
зависимости “Работник Должность | Ребенок”.
Для приведения отношения “Работник, Должность, Ребенок”.
к 4НФ необходима декомпозиция на отношения
“Работник-Должность” и “Работник – Ребенок”
Бессарабов Н.В.2018
7
8. Правилo приведения к 4НФ
Правило приведения к 4НФ: Если в отношении находящемся вНФБК обнаружены нетривиальные многозначные зависимости,
то для их исключения необходимо провести декомпозицию
используя теорему Фейгина.
Иначе говоря, если в отношении r со схемой R(X,Y,Z) имеется
нетривиальная многозначная зависимость X Y|Z, то для
перехода к 4НФ необходимо выполнить декомпозицию отношения
r на его проекции на {X,Y} и {X,Z}.
Полученные отношения не связаны между собой.
Замечание: Для обнаружения необходимости приведения к 4НФ
можно разобраться с семантикой отношения и найти в нём два
“встроенных” независимых отношения, затем найти общее поле,
соединяющее отношения, но не образующее полного ключа
ни в одном из этих отношений.
Бессарабов Н.В.2018
8
9. Многозначные зависимости. Пример 2.
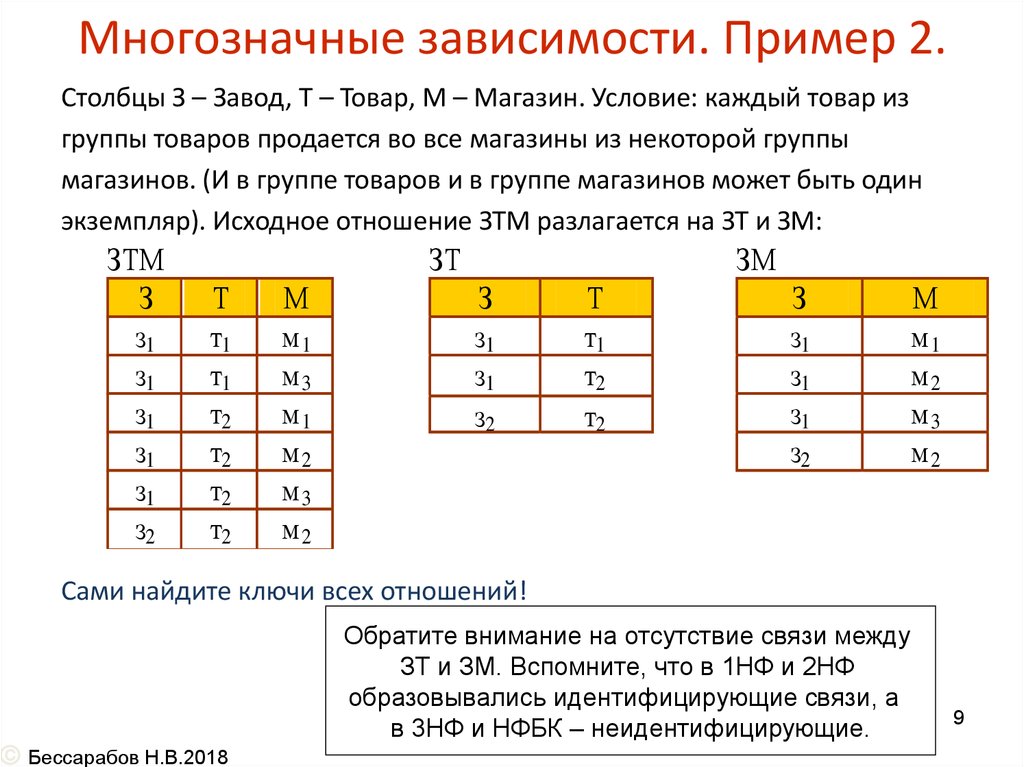
Столбцы З – Завод, Т – Товар, М – Магазин. Условие: каждый товар изгруппы товаров продается во все магазины из некоторой группы
магазинов. (И в группе товаров и в группе магазинов может быть один
экземпляр). Исходное отношение ЗТМ разлагается на ЗТ и ЗМ:
ЗТМ
З
з1
з1
з1
з1
з1
з2
ЗМ
ЗТ
Т
т1
т1
т2
т2
т2
т2
М
м1
м3
м1
м2
м3
м2
З
з1
з1
з2
Т
т1
т2
т2
З
з1
з1
з1
з2
М
м1
м2
м3
м2
Сами найдите ключи всех отношений!
Бессарабов Н.В.2018
Обратите внимание на отсутствие связи между
ЗТ и ЗМ. Вспомните, что в 1НФ и 2НФ
образовывались идентифицирующие связи, а
в 3НФ и НФБК – неидентифицирующие.
9
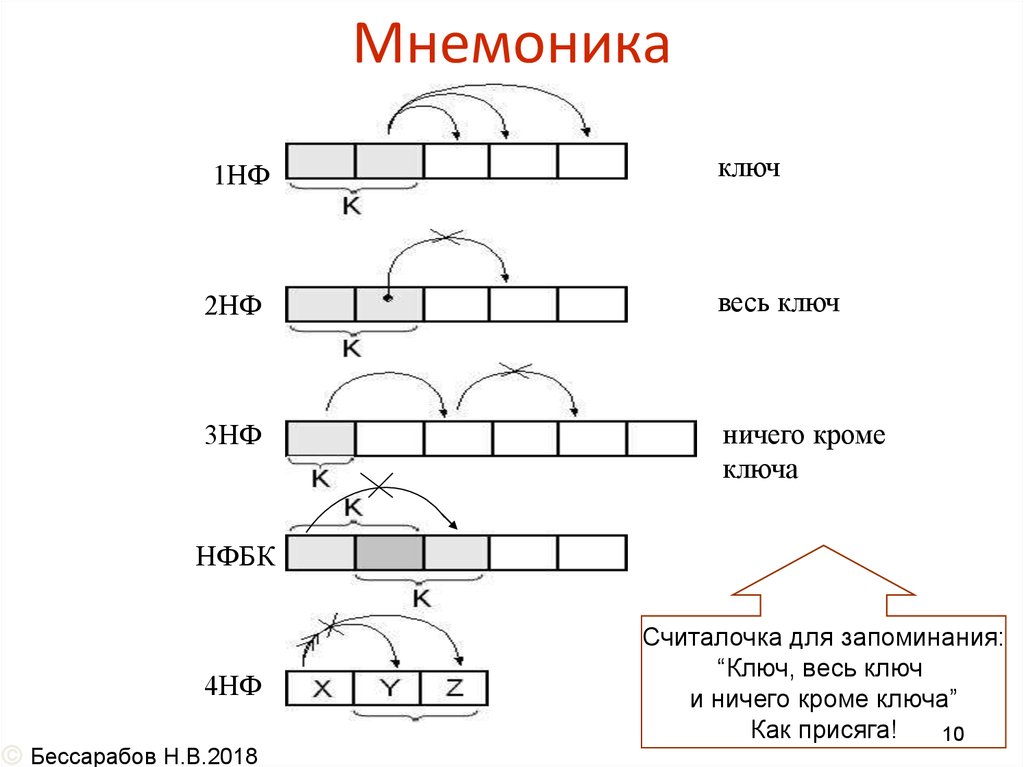
10. Мнемоника
1НФключ
2НФ
весь ключ
3НФ
ничего кроме
ключа
НФБК
4НФ
Бессарабов Н.В.2018
Считалочка для запоминания:
“Ключ, весь ключ
и ничего кроме ключа”
Как присяга!
10
11. Получение концептуальной схемы базы сразу в 3НФ и уточнения до НФБК и 4НФ:
1. Получение 3НФ: Выделите простые сущности, не содержащие в себе другиесущности и не имеющие составных атрибутов и групп однородных атрибутов.
Определите характер связей (идентифицирующая, не идентифицирующая,
обязательная, не обязательная) если они существуют.
2. Проверка 3НФ (поиск пропущенных ФЗ): Уточните семантику, найдите
ключевые атрибуты, выделив все альтернативные ключи. Чтобы окончательно
убедиться в простоте сущностей проверьте наличие ФЗ кроме зависимостей от
ключа. Если они обнаружены, декомпозируйте такие сущности по Хису.
3. Получение НФБК: Если в отношении есть пересекающиеся ключи, стоит
проверить его на НФБК. Ищите зависимости между ключевыми атрибутами не
входящими одновременно в оба пересекающихся ключа. При обнаружении таких
зависимостей получите НФБК, используя теорему Хиса.
4. Получение 4НФ: Если в исходных или полученных отношениях (в том числе при
записи в Н1НФ) обнаружены независимые многозначные атрибуты, необходимо
привести эти отношения к 4НФ используя теорему Фейгина.
Замечание 1: На всех этапах необходимо выяснять семантику сущностей, их
атрибутов и блоков атрибутов. Разработчик может внести дополнительные
элементы семантики и даже эмулировать другие модели данных.
Замечание 2: Вычислимые атрибуты в концептуальной схеме должны
выявляться, но реализовываться они будут на физическом уровне.
Бессарабов Н.В.2018
11
12. Зависимости соединения и 5НФ
4НФ не дает полного решения вопроса о декомпозицииотношений без потерь информации. Дело в том, что
рассмотрения декомпозиции на два отношения недостаточно.
Может существовать нетривиальная декомпозиция на три
отношения, но не существовать такой декомпозиции на два
отношения.
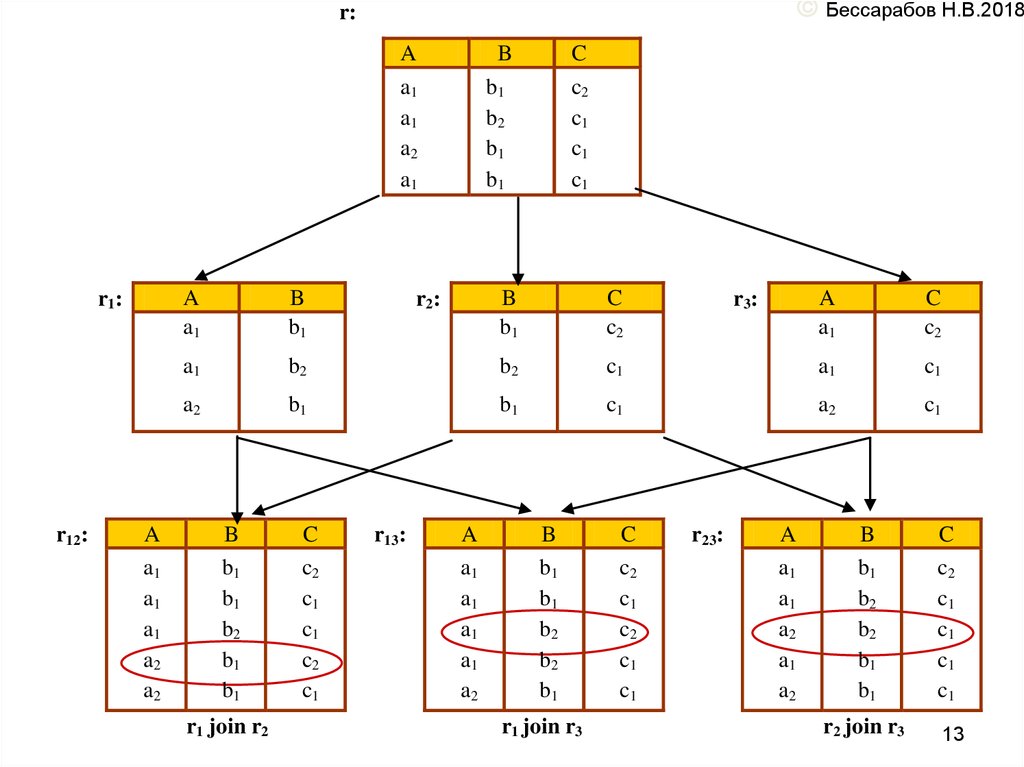
Ниже приведен пример отношения, которое нельзя
восстановить после разложения на две части, но
например, соединение, r12 join r3=(r1 join r2) join r3
восстанавливает отношение. Оказалось необходимым
использование соединения всех трёх проекций.
Бессарабов Н.В.2018
12
13.
Бессарабов Н.В.2018r:
A
a1
a1
a2
a1
r1:
r12:
A
a1
a1
a1
a2
a2
A
a1
B
b1
a1
a2
B
b1
b1
b2
b1
b1
r1 join r2
B
b1
b2
b1
b1
C
c2
c1
c1
c1
B
b1
C
c2
b2
b2
b1
b1
C
c2
c1
c1
c2
c1
r2:
r13:
A
a1
a1
a1
a1
a2
B
b1
b1
b2
b2
b1
r1 join r3
A
a1
C
c2
c1
a1
c1
c1
a2
c1
C
c2
c1
c2
c1
c1
r3:
r23:
A
a1
a1
a2
a1
a2
B
b1
b2
b2
b1
b1
r2 join r3
C
c2
c1
c1
c1
c1
13
14. Определение зависимости проекция - соединение
Определение зависимости проекция соединениеТо, что отношение r восстанавливается соединением
всех трех проекций, но не любых двух означает, что
между атрибутами отношения r имеется зависимость,
но эта зависимость не является ни функциональной, ни
многозначной.
Определение зависимости проекция - соединение:
Пусть r отношение на подмножествах атрибутов A1, A2, …An,
может быть пересекающихся. Отношение r удовлетворяет
зависимости соединения тогда и только тогда, когда оно
равносильно соединению всех своих проекций на
подмножества атрибутов A1, A2, …An,
то есть:
R=(proj {A1} r) join (proj {A2} r) join … join (proj {An} r)
Бессарабов Н.В.2018
14
15. Зависимость проекция - соединение как обобщение MV-зависимости
Связь расширений функциональной зависимости:Отношение r со схемой R(X,Y,Z) удовлетворяет
зависимости соединения *(XY,XZ) если имеется
многозначная зависимость X Y|Z .
Пояснение: MV-зависимость является частным
случаем зависимости соединения. Если в
отношении имеется многозначная зависимость, то
имеется и зависимость соединения. Обратное
неверно.
Бессарабов Н.В.2018
15
16. Нетривиальная зависимость соединения
Определение (нетривиальной зависимостисоединения). Зависимость соединения *(A1, A2, …An)
называется нетривиальной зависимостью соединения,
если выполняются условия:
• хотя бы одно из подмножеств атрибутов A1, A2, …An не
содержит потенциального ключа отношения;
• ни одно из подмножеств атрибутов A1, A2, …An не
совпадает со всем множеством атрибутов отношения.
Бессарабов Н.В.2018
16
17. Тривиальная зависимость соединения
Определение тривиальной зависимости cоединения:Зависимость соединения *(A1, A2, …An) называется
тривиальной зависимостью соединения, если
выполняется одно из условий:
• все множества атрибутов A1, A2, …An содержат
потенциальный ключ отношения r.
• одно из множеств атрибутов A1, A2, …An совпадает со
всем множеством атрибутов отношения r.
Бессарабов Н.В.2018
17
18. Пятая нормальная форма
Определение (5НФ): Отношение находится в пятойнормальной форме (5НФ) тогда и только тогда, когда
любая имеющаяся зависимость соединения является
тривиальной.
Определение (5НФ): Отношение находится в пятой
нормальной форме (5НФ) если оно не содержит
нетривиальных зависимостей соединения.
Отрицание определения 5НФ: Отношение не находится
в 5НФ, если в отношении найдется нетривиальная
зависимость соединения.
Бессарабов Н.В.2018
18
19. Правило нормализации для 5НФ
Приведение к 5НФ: Если в отношенияхобнаружены нетривиальные зависимости
соединения, то для их исключения
необходимо провести декомпозицию на
выделенные подмножества атрибутов
A1, A2, …An.
Бессарабов Н.В.2018
19
20. Когда нужна нормализации до 5НФ
• Пятая нормальная форма может понадобиться для преобразования схемы изтрёх и более сущностей связанных между собой исключительно отношениями
многие-ко-многим. Стандартное преобразование каждой такой связи с
помощью ассоциативной сущности может привести к появлению
присоединённых записей при выполнении некоторых запросов.
• Для их устранения необходимо создать дополнительную сущность
связывающую все исходные отношения.
Замечание: Схемы, в которых нарушается 5НФ встречаются очень редко.
Пример: схема из трёх сущностей со связями многие-ко-многим, а именно
-- автомобиль;
-- цвет кузова;
-- модель.
Ассоциативные сущности: модель – цвет, автомобиль – цвет, автомобиль –
модель.
Добавляем ассоциативную сущность модель – цвет - автомобиль.
21. Понятие о нормальной форме домен-ключ
Понятие о нормальной форме доменключОпределение (НФДК, DKNF): Отношение
находится в нормальной форме Домен/Ключ если
каждое ограничение отношения есть логическое
следствие определений ключей и доменов.
Р. Фейгин доказал, что отношение в нормальной
форме домен/ключ не имеет никаких аномалий
модификации и, с другой стороны, отношение не
имеющее аномалий модификации находится в
нормальной форме домен/ключ.
Бессарабов Н.В.2018
21
22. Известные понятия, использованные в определении НФДК
• Ограничение это правило заданное длястатических значений атрибутов с помощью
Функциональных зависимостей
Многозначных зависимостей
Ограничений на значения атрибутов
Ограничений типа бизнес-правил
• Домен это множество допустимых значений.
Содержит:
Описание физического уровня
Описание логического уровня
• Ключ: Наборы атрибутов, однозначно
определяющие запись в отношении.
Бессарабов Н.В.2018
22
23. Пример НФДК. Исходное отношение
Отношение STUDENT и два ограничения:Схема отношения:
STUDENT (SID, GradeLevel, Building, Fee)
Ключ: SID
Ограничения:
• Building ------> Fee
• SID не может начинаться с цифры
Бессарабов Н.В.2018
23
24. Пример НФДК. Отношение в НФДК.
• Отношения и определения ключейSTUDENT (SID, GradeLevel, Building)
BLDG-FEE ( Building, Fee)
• Определения доменов:
SID
GradeLevel
Building
Fee
Бессарабов Н.В.2018
в формате CDDD, где C
десятичная цифра, не равная
1, а D любая десятичная цифра
домен {'FR', 'SO', 'JR', 'SR'}
домен CHAR(4)
домен DEC(4)
24
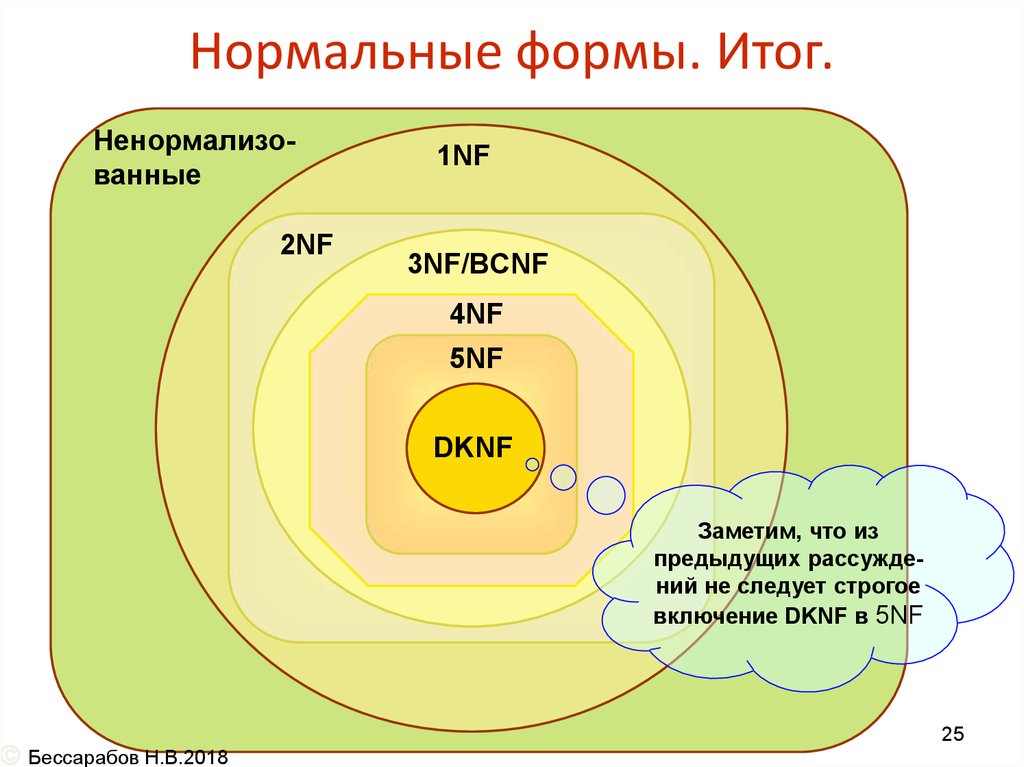
25. Нормальные формы. Итог.
Ненормализованные2NF
1NF
1NF
2NF
3NF/BCNF
3NF/BCNF
4NF
4NF
5NF
5NF
DKNF
DKNF
Заметим, что из
предыдущих рассуждений не следует строгое
включение DKNF в 5NF
Бессарабов Н.В.2018
25
26. Понятие о денормализации
“Акуля, Акуля, а чо ты шьёшь не оттуля?”“Так я ж, матушка, ещё пороть буду”
Программистская мудрость
Как известно, база данных это не только то, что в ней содержится, но
и то, что в ней можно спросить и что фактически спрашивают.
Во всех возможных вариантах семантики моделей данных
отображается только аспект получения правильного результата, но не
время исполнения, не размерные параметры (число кортежей, объём
данных ширина строки и т.д.). В реализациях же семантика
расширяется и время выполнения -- важнейший параметр.
Нормализация повышает производительность операций
манипулирования данными и простых запросов, не требующих
соединения данных из многих таблиц.
Анализ потока запросов может показать, что для повышения
производительности схема нормализованной базы нуждается в
преобразовании, не соответствующем требованиям нормализации.
Такие преобразования называют денормализацией.
Как правило, денормализация ускоряет некоторые запросы, но
замедляет и усложняет манипулирование данными.
Бессарабов Н.В.2018
26
27. Пример денормализации
Так называемая сверхномализация.Обнаружено, что запросы к проблемной таблице Tab1 обращаются чаще
к коротким столбцам 1, 2, 5, 6 шириной, например, по 5 байт, чем к
широким столбцам 3 и 4 шириной 12 кбайт и 64 кбайт, соответственно.
Ключ образуют столбцы 1 и 2.
Проведем денормализацию. Разделим таблицу на две – Tab1_1,
включающую широкие столбцы 3, 4, и Tab1_2 с узкими столбцами. Ключ у
новых таблиц тот же. Скорость запросов извлекающих столбцы 1, 2, 5, 6
возрастет, но теперь вместо одной команды вставки, удаления и обновления
исходной таблицы необходимо выполнять по две соответствующих команды
для Tab1_1 и Tab1_2, причём обе команды должны быть выполнены
обязательно.
А как этого добиться?
1 PK
1 PK
1 PK
Tab1
2 PK 3
Tab1-1
2 PK 3
Tab1_2
2 PK 5
Бессарабов Н.В.2018
4
5
6
4
6
Обратите внимание на то, что между Tab1_1 и Tab1_2
27
использована редко встречающаяся связь 1:1
28. Нисходящая денормализация
Имеет смысл только если столбец Name часто используется взапросах к таблице Order_2, когда эти запросы критические, то есть
используют достаточно много ресурсов. Соединение таблиц даст тот
же результат, но запрос будет работать медленнее.
29. Восходящая денормализация
Сумма заказа totalвычисляется как сумма
строк заказа subtotal
30. Заключение
Рассмотрены нормальные формы высших порядков 4НФ и 5НФ,основанные на расширении понятия функции – многозначных
зависимостях и зависимостях соединения (проекции – соединения).
В практике эти формы встречаются очень редко.
Введенное Р. Фейгиным понятие нормальной формы “домен –
ключ” не используется при разработке баз данных, однако оно
положило конец дальнейшим поискам нормальных форм.
Процесс разработки схемы базы не заканчивается
нормализацией. На следующем этапе следует вспомнить, что база
данных это не только то, что в ней хранится, но и то, о чем в ней
спрашивают. По результатам анализа критических запросов может
быть выполнена частичная денормализация схемы. В результате
удается ускорить выполнение некоторого набора запросов, но
возрастает время исполнения операторов манипуляции данными и
усложняется, может быть существенно, процедурная часть
приложения.
Бессарабов Н.В.2018
30
31. Основные понятия (1/2)
Бессарабов Н.В.201831
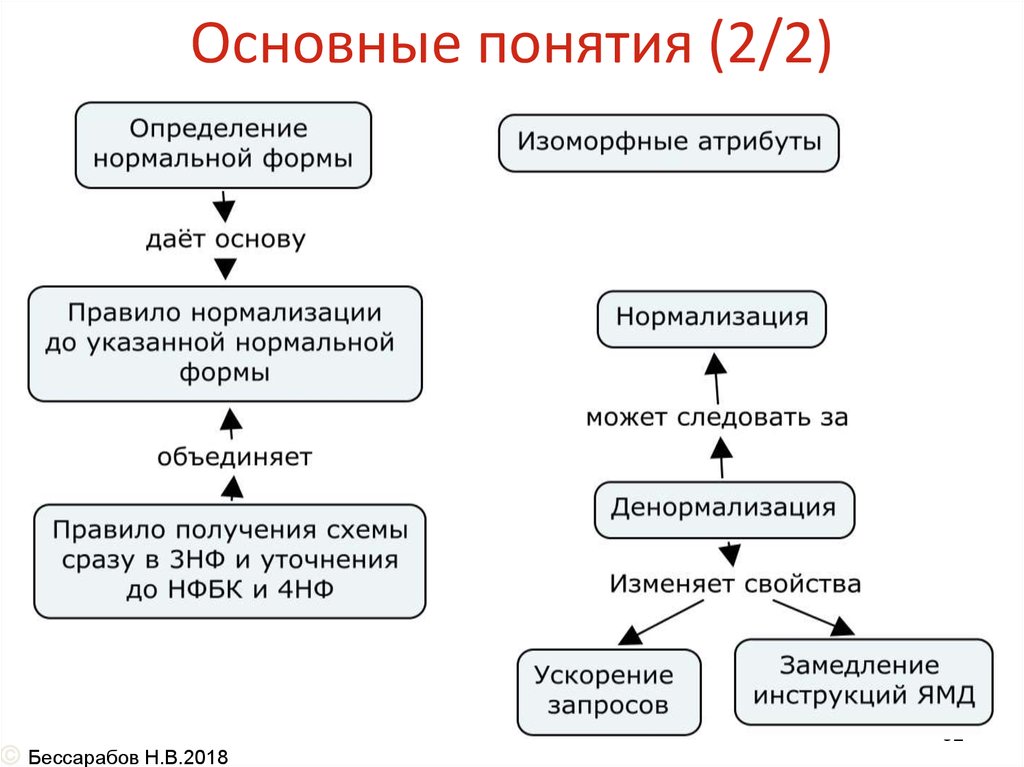
32. Основные понятия (2/2)
Бессарабов Н.В.201832
33. Словарь студента (1/2)
• Многозначные зависимости.MV- зависимость (Multivalued dependency)- Пусть R – отношение, а X,Y,Z -непересекающиеся множества его атрибутов. Атрибуты Y и Z многозначно
зависят от X (обозначение X
Y|Z) если из того, что в отношении
R
содержатся кортежи r1 = (x, y, z1) и r2 = (x, y1, z) следует, что в отношении R
содержится также кортеж r3 = (x, y, z).
• Теорема Фейгина.
Пусть на множестве атрибутов R выделены три непересекающиеся
подмножества X,Y,Z. Декомпозиция отношения R на проекции {X,Y} и
{X,Z} будет декомпозицией без потерь тогда и только тогда, когда
имеется многозначная зависимость X Y|Z .
• Зависимости соединения
–Пусть r отношение на множестве
атрибутов A1, A2, …An, может быть пересекающихся. Отношение r
удовлетворяет зависимости соединения тогда и только тогда, когда
оно равносильно соединению всех своих проекций на подмножества
атрибутов A1, A2, …An, т.е.
R=(proj {A1} r) join (proj {A2} r) join … join (proj {An} r)
Бессарабов Н.В.2018
33
34. Словарь студента (2/2)
• Нетривиальная зависимость – Зависимость соединения*(A1, A2, …An) называется нетривиальной зависимостью соединения,
если выполняются условия:
- Одно из множеств атрибутов A1, A2, …An не содержит потенциального
ключа отношения.
- Ни одно из множеств атрибутов A1, A2, …An не совпадает со всем
множеством атрибутов отношения.
• 5НФ – Отношение находится в пятой нормальной форме (5НФ) тогда
и только тогда, когда любая имеющаяся зависимость соединения
является тривиальной.
• НФДК - Отношение находится в нормальной форме Домен/Ключ
если каждое ограничение отношения есть логическое следствие
определений ключей и доменов.
• Денормализация - Анализ потока запросов может показать, что схема
нормализованной базы нуждается в преобразовании, не
соответствующем требованиям нормализации. Такие преобразования
называют денормализацией.
Бессарабов Н.В.2018
34





























 database
database








