Расчеты освещения от больших поверхностей. Формула В.А. Фока

1.

Расчеты освещения от больших
поверхностей. Формула В.А. Фока
E-mail: [email protected]
сот: 8-910-443-75-52
Подготовил: Смирнов П.А.

2.

Фок, Владимир Александрович
(22 декабря 1898 г. – 27 декабря 1974 г. Санкт-Петербург)
Освещённость от поверхностей произвольной
формы – труды ГОИ – 1924 г. – 26 лет.
• Квантовая механика, квантовая
электродинамика, квантовая теория
поля
• Пространство Фока
• Метод функционалов Фока
• Метод собственного времени
• Многовременной формализм
• Метод Хартри-Фока «Метод
самосогласованного поля»
• и т.д.

3.

По статье В.А. Фока «Освещённость от
поверхностей произвольной формы»
Принимая яркость поверхности L=1
1
cos(N, r ) cos(n, r )dS
E
r2
Разложение по осям:
1 cos( N, r ) cos(r, x) dS
Ex
r2
1 cos( N, r ) cos(r, y ) dS
E y
2
r
1 cos( N, r ) cos(r, z ) dS
Ez
r2

4.

По статье В.А. Фока «Освещённость от
поверхностей произвольной формы»
Разложение через координаты для Ex:
r 2 х х y y z z
2
2
2
х х
y y
z z
cos(r, x)
;cos(r, y )
;cos(r, z )
r
r
r
х х
y y
z z
cos(N, r )
cos( N, x)
cos( N, y )
cos( N, z )
r
r
r
2 x x 2
r 4 cos(N, x)
2 x x y y
cos(N, y )
4
r
2 x x z z
cos(N, z ) dS
4
r
1
Ex
2

5.

По статье В.А. Фока «Освещённость от
поверхностей произвольной формы»
1
Ex
2
A cos(N, x) B cos(N, y) C cos(N, z) dS
где:
A
B
C
2 x x
2
r4
2 x x y y
r4
2 x x z z
r4
P 0
R Q 2 x x
y z
r4
z z
r2
y y
R 2
r
P R 2 x x y y
z x
r4
Q P 2 x x z z
x y
r4
Что есть ротор вектора (P,Q,R):
Q
2

6.

По статье В.А. Фока «Освещённость от
поверхностей произвольной формы»
Используем теорему Стокса:
1
E
x
2
1
E
y
2
1
Ez
2
С
С
y y dz z z dy
r2
z z dx x x dz
r2
x x dy y y dx
r2
С
Введём в рассмотрение вектор:
1
V
x
2
1
V
y
2
1
Vz
2
lg rdx
С
lg rdy
С
lg rdz
С
тогда:
Vz Vy
Ex
y
z
V V
Ey x z
z
x
Vy Vz
Ez
x
y
Vx Vy Vz
0
x
y
z

7.

Выражения для потока
Ф12 Ex cos(n, x) E y cos(n, y ) Ez cos(n, z ) dS 2
S2
Т.к. вектор E – это ротор, то можно ещё раз применить теорему Стокса:
Ф12 Vx dx Vy dy Vz dz
С
или
1
Ф12
2
1
Ф12
2
lg r dxdx dydy dzdz
С C
lg r cos ds, ds dsds
С C

8.

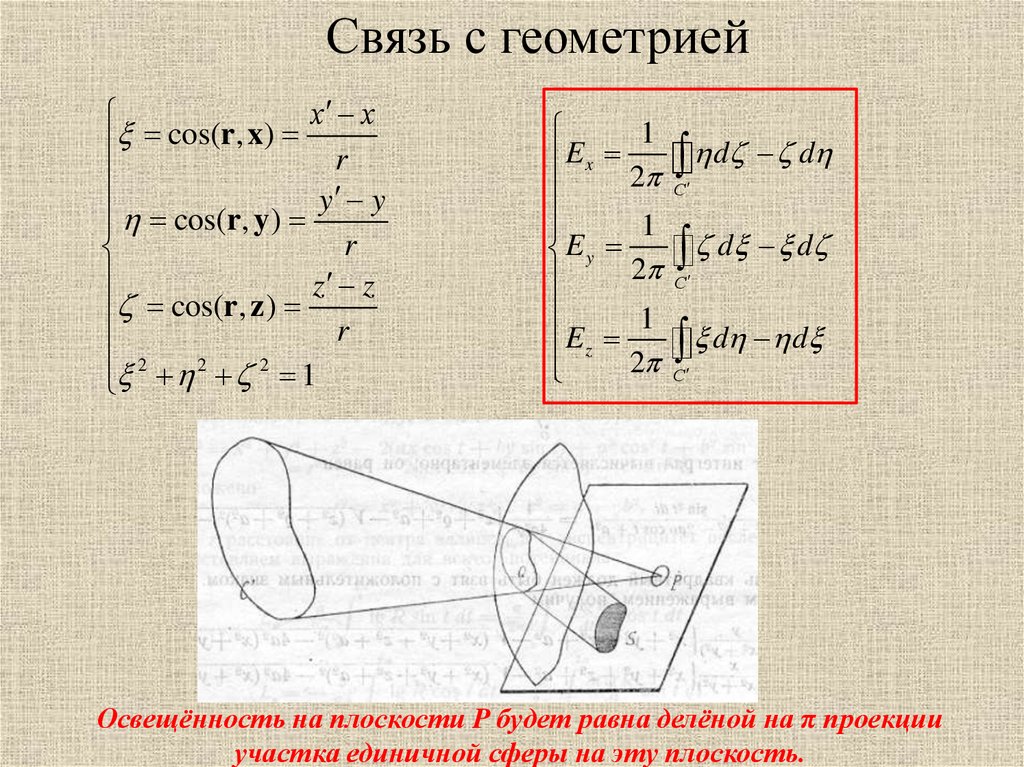
Связь с геометрией
х х
cos(r, x) r
cos(r, y ) y y
r
z z
cos(r, z )
r
2 2 2 1
1
E
d d
x
2 С
1
E
d d
y
2 С
1
d d
Ez
2 С
Освещённость на плоскости P будет равна делёной на π проекции
участка единичной сферы на эту плоскость.

9.

Расчёт освещённости от равнояркой
поверхности
d
Световой вектор:
E LdΩ
Расчётная точка
Освещённость:
E Ld
или
L
E cos d
2C
- угол между внешней стороной
образующей конической поверхности
и расчётной плоскостью
Для многоугольника можно
перейти от интеграла к сумме:
L N
E cos i i
2 i 1

10.

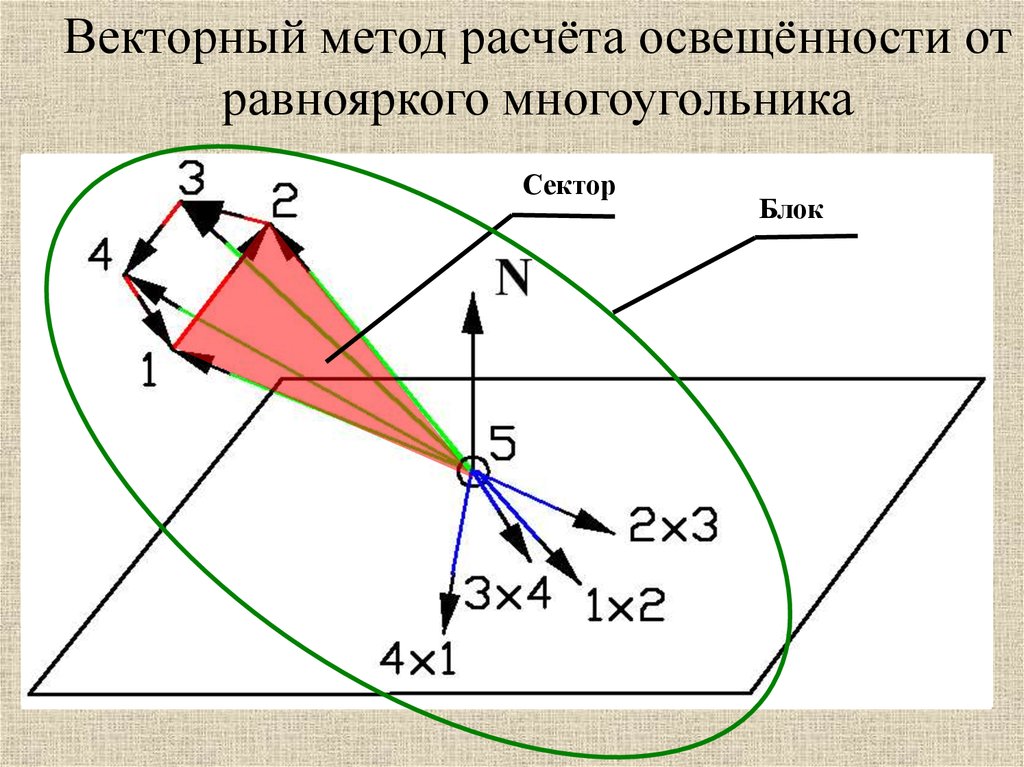
Векторный метод расчёта освещённости от
равнояркого многоугольника
Сектор
Блок

11.

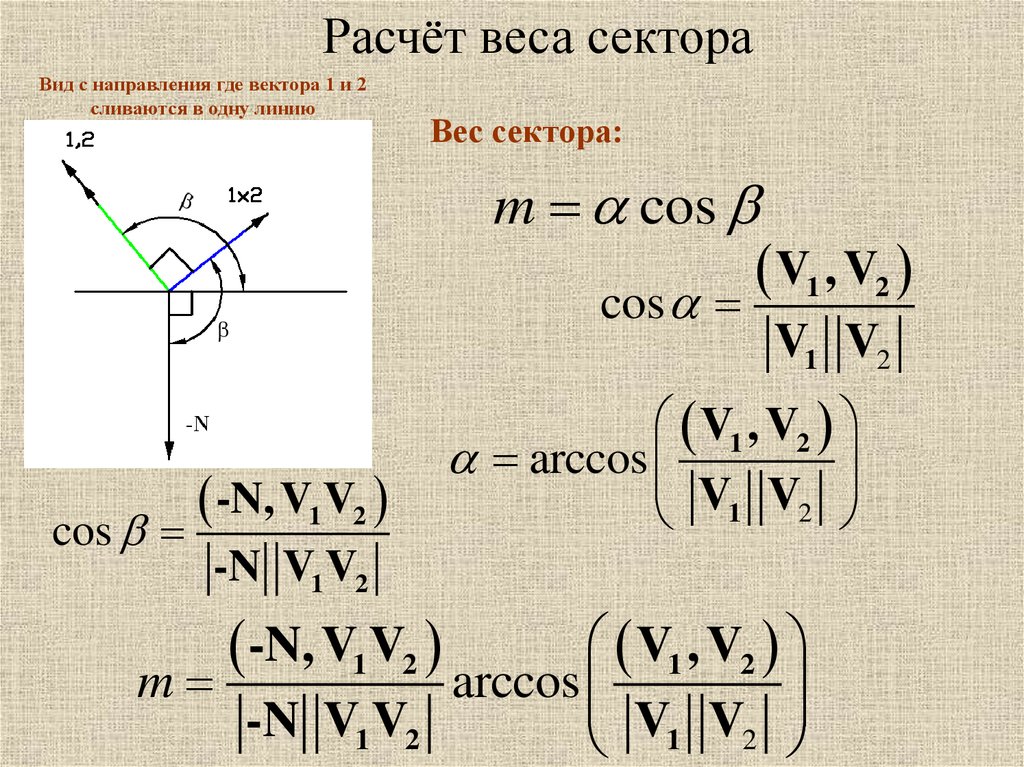
Расчёт веса сектора
Вид с направления где вектора 1 и 2
сливаются в одну линию
Вес сектора:
m cos
V1 , V2
cos
V1 V2
-N, V1V2
cos
V1 , V2
arccos
V1 V2
-N V1V2
V1 , V2
-N, V1V2
m
arccos
-N V1V2
V1 V2

12.

Расчёт проекции телесного угла
(форм-фактора) блока
Форм-фактор блока
N
F mi
i 1
N 1
F
i 1
N
F i cos i
i 1
-N, Vi Vi 1 arccos Vi , Vi 1
-N Vi Vi 1
Vi Vi 1
VN , V1
-N, VN V1
arccos
-N VN V1
VN V1

13.

Спасибо за внимание!