Начисление процентов по сложным ставкам

1. Начисление процентов по сложным ставкам

Князева М.А., доцент,
канд. техн. наук
1

2. Происхождение сложного процента и срочного вклада

• Сложный процент восстанавливает справедливость, он уравнивает
«ленивого» и «активного» клиентов. Переоформление вклада ничего
не приносит банкиру, кроме хлопот, поэтому он сам должен начислять
сложный процент.
• Во избежание процедуры изъятия и повторного вклада обе стороны
кредитной или депозитной сделки заранее договариваются об
использовании сложных процентов и срочных вкладов «в одном
флаконе».
• В стабильных экономических условиях при многолетнем сроке
кредита применение сложного процента является неписаным
стандартом. Но год –это большой срок. Поэтому многие российские и
иностранные банки начисление сложных процентов по кварталам, а в
условиях высокой инфляции и по месяцам.
В кредитных договорах и банковских правилах это звучит примерно
так: «Ежеквартально сумма вклада увеличивается на ... процентов»
или «Проценты по вкладу капитализируются каждые три месяца»
или «Сумма процентов по вкладу прибавляется к основному вкладу
раз в три месяца».
2

3. НАЧИСЛЕНИЕ СЛОЖНЫХ ПРОЦЕНТОВ

• В отличие от схемы простых процентов, где процент начисляется на
одну и ту же величину долга или депозита (базу), в схеме сложных
процентов начисленные проценты присоединяются к первоначальной
сумме.
• Присоединение начисленных процентов к сумме, которая послужила
базой для их начисления называют капитализацией.
Период (12%
годовых – 1% в
месяц)
Сумма на депозите
Начало 1 месяца
100тыс
Конец первого
месяца
100тыс
1000
Конец второго
месяца
100тыс
1000
Конец третьего
месяца
100тыс
1000
1010
Начисленный процент
1010
1020,1
100тыс
Х 1% = 1000
100тыс
1000
1000
100тыс
1010
Х 1%= 1010
Х 1%= 1020,1
3

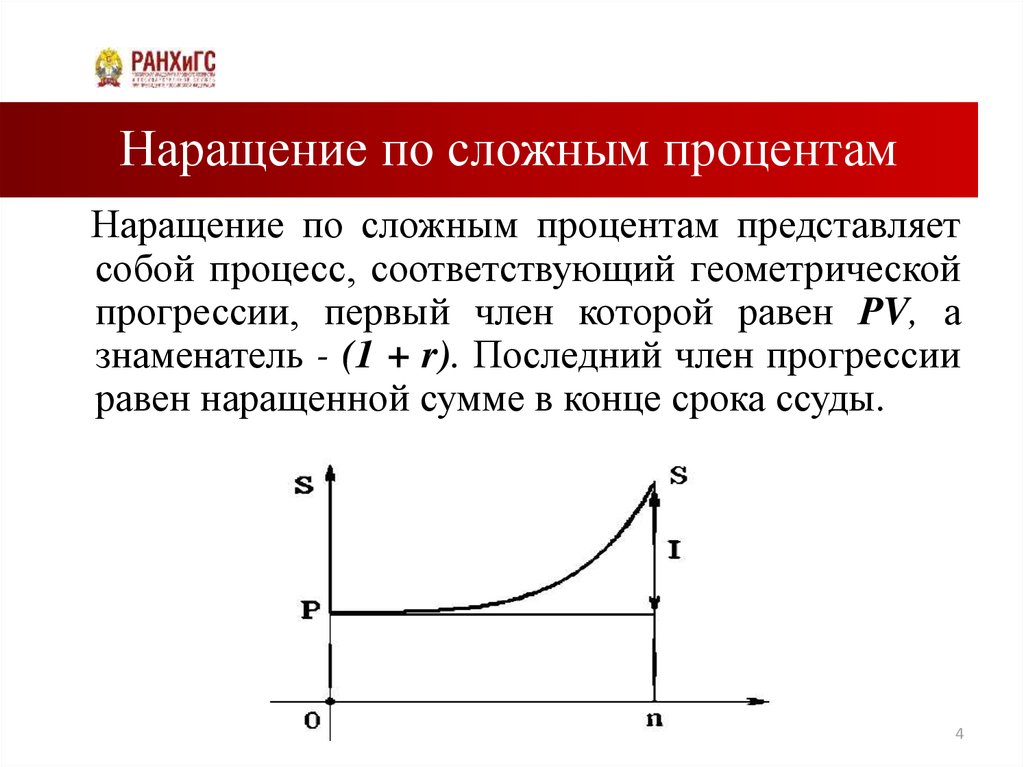
4. Наращение по сложным процентам

Наращение по сложным процентам представляет
собой процесс, соответствующий геометрической
прогрессии, первый член которой равен РV, а
знаменатель - (1 + r). Последний член прогрессии
равен наращенной сумме в конце срока ссуды.
4

5. Иллюстрация мощи сложного процента

• Сложный процент дает приращение вклада в
геометрической прогрессии, а простой процент -в
арифметической. При больших сроках разница может
быть впечатляющей.
• Классический пример с «покупкой» острова Манхэттен,
где сейчас расположен центр Нью-Йорка, у индейского
вождя за 24 доллара в 1624 году. Если бы эти деньги
удалось положить в банк всего под 6,3% годовых
(средний процент по долгосрочным займам в ХХ веке в
США), то спустя 390 лет, в 2014 году, была бы
накоплена сумма примерно 534 791 388 000 долл.
• При простом проценте накопленная сумма была бы
ничтожной: 24*(1+ 0,063*390) = 613,68 долл.
5

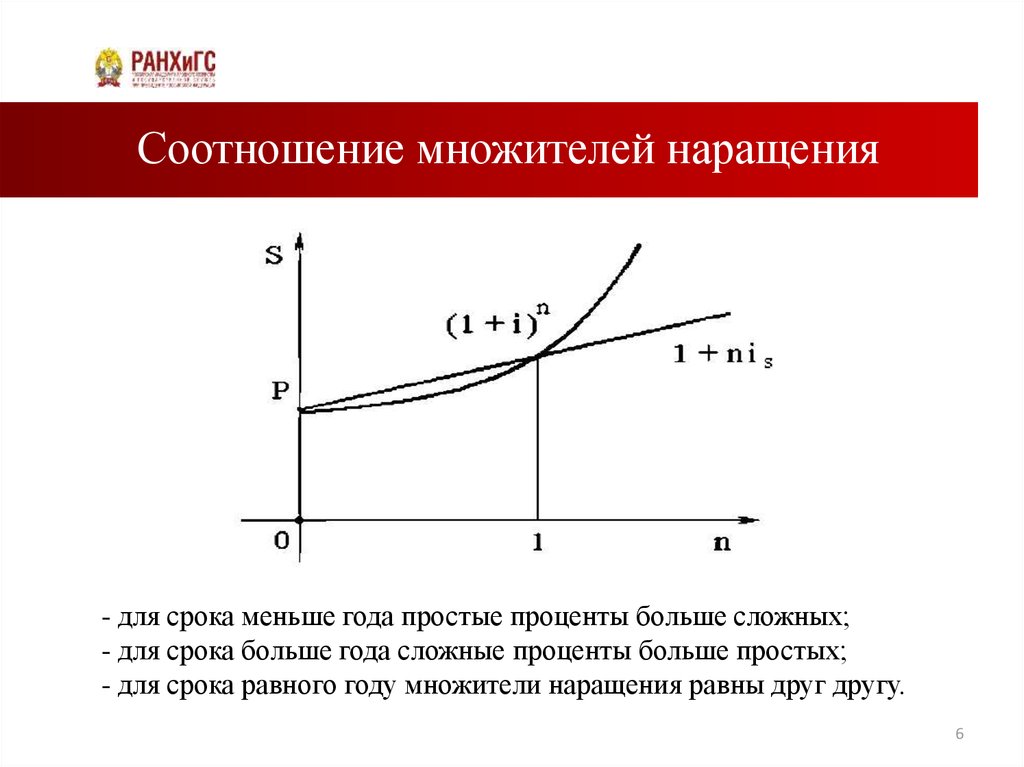
6. Соотношение множителей наращения

- для срока меньше года простые проценты больше сложных;
- для срока больше года сложные проценты больше простых;
- для срока равного году множители наращения равны друг другу.
6

7. Декурсивный метод начисления сложных процентов. Модель наращения

Формулу вычисления S называют основной моделью
сложного процента.
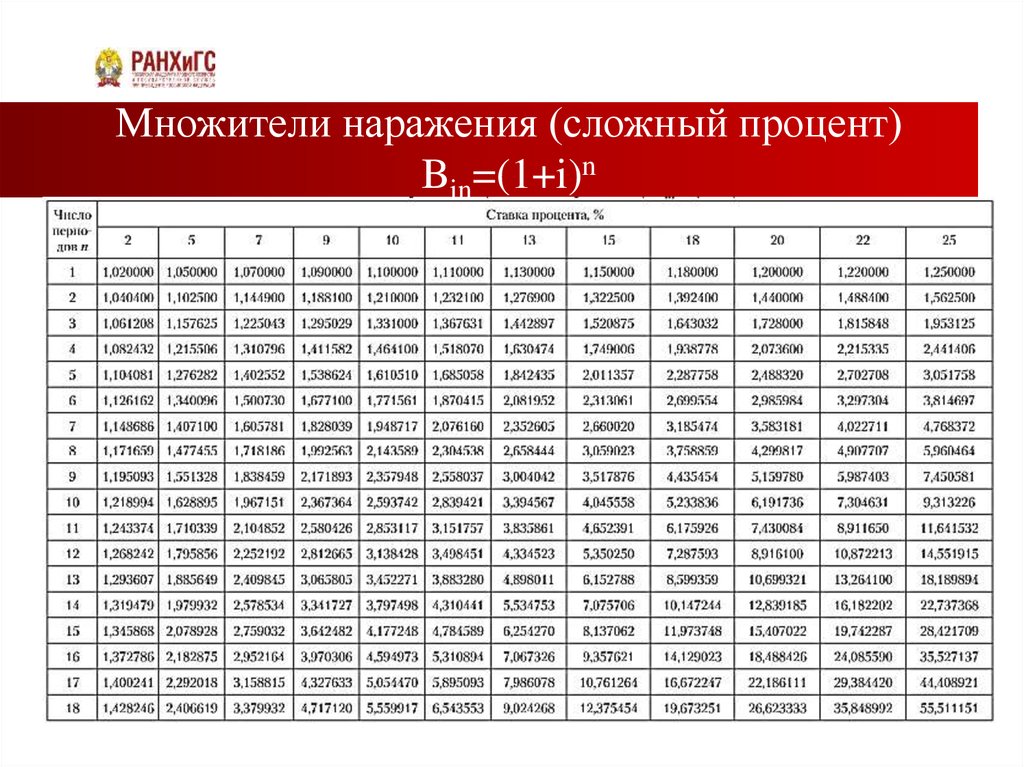
Значения множителя наращения табулированы для
наиболее часто встречающихся значений I и n (слайд)

8. Множители наражения (сложный процент) Bin=(1+i)n

9. ПРИМЕР 1

9

10. Декурсивный способ начисления сложных процентов. Модель дисконтирования

10

11. Антисипативный метод начисления сложных процентов. Модель дисконтирования

Формулу вычисления P называют основной
моделью сложного дисконта
11

12. Пример 2

12

13. Антисипативный метод начисления сложных процентов. Модель наращения

13

14. Пример 3

14

15. Начисление процентов по сложной переменной ставке. Модель наращения при декурсии

15

16. Пример 4

16

17. Годовая номинальная процентная ставка

Годовая номинальная ставка, конвертируемая m раз в год
– процентная ставка, определяемая с учетом процентной
ставки за один период начисления процентов и числа
периодов начисления процентов в m раз
17

18. Начисление процентов по годовой номинальной ставке

Наращение
Дисконтирование
18

19. Пример 5

19

20. Пример 6

20

21. Пример 7

21

22. Начисление процентов по непрерывной ставке

22

23. Модели начисления непрерывных процентов

23

24. Пример 8

24

25. Модель доходности операций при начислении сложных процентов

25

26. Пример 9

26

27. Эквивалентные сложные ставки

27

28. Пример 10

28

29. Эффективные ставки, эквивалентные номинальным ставкам

29

30. Пример 11

30