Similar presentations:
Chemical potential. Chemical potential of an ideal gas
1. Teacher of dicepline: Altynbekova M.O. Prepared by: Asan Asel Group : JHM-611F
MINISTRY OF EDUCATION AND SCIENCE OF THE REPUBLIC OF KAZAKHSTANK.A.YASSAWI INTERNATIONAL KAZAKH-TURKISH UNIVERSITY
FACULTY OF NATURAL SCIENCE
DEPARTMENT OF ECOLOGY AND CHEMSTRY
The theme:
Chemical potential. Chemical potential of an
ideal gas
Teacher of dicepline: Altynbekova M.O.
Prepared by: Asan Asel
Group : JHM-611F
2. Free Energy and Equilibria
FREE ENERGY AND EQUILIBRIADG < 0 process is spontaneous
DG > 0 reverse process is spontaneous
DG = 0 no change is spontaneous: Equilibrium
Le Châtelier’s principle gives us some understanding of how the
equilibrium of a system changes when we perturb it.
"Any change in one of the variables that determines the state of a system in
equilibrium causes a shift in the position of equilibrium in a direction that
tends to counteract the change in the variable under consideration."
We are interested in how systems tend towards equilibrium and what
obstacles keep them out of equilibrium.
The free energy, or more correctly, the chemical potential is our measure
of roughly how far we have to go to come to equilibrium. It is a potential
energy of sorts.
3. Chemical Potential
CHEMICAL POTENTIALThe chemical potential can be used to give quantitative meaning to Le
Châtelier’s principle.
Chemical potential of component A, µA, is defined as the partial molar Gibbs
free energy:
G
A
n A T, P, n
j n A
This is the change in G with respect to a infinitesimal change in the amount
of component A with all other parameters held constant.
It is essentially the free energy increase (or decrease) associated with
adding a little of A to the system.
4. Directionality of a Chemical Reaction
DIRECTIONALITY OF A CHEMICAL REACTIONConsider a closed system of four components (A, B, C, and D) undergoing a
reversible chemical reaction:
aA bB cC dD
dG SdT VdP AdnA BdnB C dnC DdnD
In a closed system,
At constant T and P,
dn A dn B
dn
dn
c d d
a
b
c
d
dG i dni
i
(c C d D a A b B )d
a A b B c C d D d
At equilibrium:
a A b B c C d D
dn A ad
dnB bd
5. Example
EXAMPLEH2O (l)
100 °C
H2O (g)
This is at constant T and P. Its reversible. So,
DG°vap= 0 = DH°vap-T DS°vap
Note that this implies at equilibrium:
H 2 O(l) H 2 O(g)
6. Chemical Potential and Partial Pressure
CHEMICAL POTENTIAL AND PARTIAL PRESSUREP
We found last time that: G P2 G P1 nRT ln 2
P1
(T = constant)
Defining the standard state: G P 1atm G0
1
Then,
and,
so,
P
0
G P G nRT ln
1atm
G
A
n A T, P, n n
j
0 RT ln
A
P
1atm
In a mixture, the chemical potential of A can thus be expressed in
terms of its partial pressure and its standard (pure) chemical
potential:
A 0A RT ln
PA
1atm
7. DG of Mixing
DG OF MIXINGConsider the isobaric, isothermal mixing of two gases:
Gas A
at
P Atm
Gas B
at
P Atm
Gas A+B
at
P Atm (total)
DGmix nA RT ln X A nB RT ln XB
DGmix TDSmix
DSmix nA Rln X A nB Rln X B
Xi
ni
nj
Mole Fraction component i
j
XA
nA
nB
and X B
n A nB
nA nB
8. Equilibrium Constant
EQUILIBRIUM CONSTANTThe Haber process of nitrogen fixation:
N2 + 3H2
2NH3
DG 2 NH3 N 2 3 H 2
0
PNH3 0
PN 2 0
PH 2
N RT ln
3 H RT ln
2 NH3 RT ln
2
2
1atm
1atm
1atm
Rewrite letting Pi
Pi
unitless pressure ratio. No units inside “ln”.
1atm
0
DG 2 0NH3 0N 2 3 H
RT 2 ln PNH3 ln PN 2 3ln PH2
2
P 2
NH3
0
DG RT ln
3
P
P
N 2 H 2
a
We have used the identity: aln x ln x
9. Equilibrium Constant
EQUILIBRIUM CONSTANTAt any temperature and pressure there exists and equilibrium state for
this reaction.
A combination of
PN2 , PH 2 , PNH3 such that DG = 0.
P 2
NH3
0
DG DG RT ln
3
P
P
N 2 H2
P 2
NH3
0
0 DG RT ln
3
P
P
N 2 H2
P 2
NH3
0
DG RT ln
3
P
P
N 2 H 2
This equation holds for equilibrium values of PN2 , PH 2 , PNH3
10. Equilibrium Constant
EQUILIBRIUM CONSTANTP
DG RT ln
eq 2
NH3
0
3
eq
eq
P
P
N 2 H 2
Define equilibrium constant (at constant T and P):
K
PNeq
PHeq
2
eq
PNH
3
2
More generally:
0
DG RT ln K
3
2
K
aA + bB
cD + dD
n
eq n
P
P
i
i
products
products
eq c
PC
eq a
PA
i
Most generally:
K
Pi
reac tan ts
eq n i
i
Q
Pi
reac tan ts
ni
eq d
PD
eq b
PB
11. Chemical Potential Example
CHEMICAL POTENTIAL EXAMPLEActivation barrier
Reactants
Reactants
D
Products
D
Products
Chemical potential is a measure of the thermodynamic free energy.
It tells us what the equilibrium distribution of reactants and products must be
It does not tell us the kinetic rate.
12. Equilibrium Example
EQUILIBRIUM EXAMPLEOxidation of CO:
2 CO (g) + O2 (g)
2 CO2 (g)
The free energy change for this reaction is simply:
DG ° rxn= 2 DG°289(CO2) - 2 DG°289(CO) - DG°289(O2)
We can calculate this using numbers from the appendix:
DG ° rxn= 2 (-394.36) - 2( -137.17) - 0 (kJ/mol) = -514.38 kJ/mol
A relatively large negative number.
eq
eq 2
PO PCO
eq
DG ° rxn= -RTlnK
K=
e514,380/RT=
e207
=
PCO
2
2
2
The equilibrium for this reaction lies far in favor of the products.
Large negative DG means the reaction goes forward with high probability.
13. Equilibrium Example
EQUILIBRIUM EXAMPLEThe conversion of CO and O2 to CO2 is
energetically favorable, but the reaction is slow
Reactants
(CO,O2) D , DG
Products (CO2)
1) We have to first break an O-O double bond
2) The resultant atoms of oxygen must
then react with CO.
Reaction coordinate
For other reactions like
2 H2(g) + O2(g)
2 H2O (l)
We need a catalyst (e.g. platinum surface), and ideally we wish to convert the
released energy to work.
Catalysts enable a reaction to take an alternative path, with lower activation barrier.
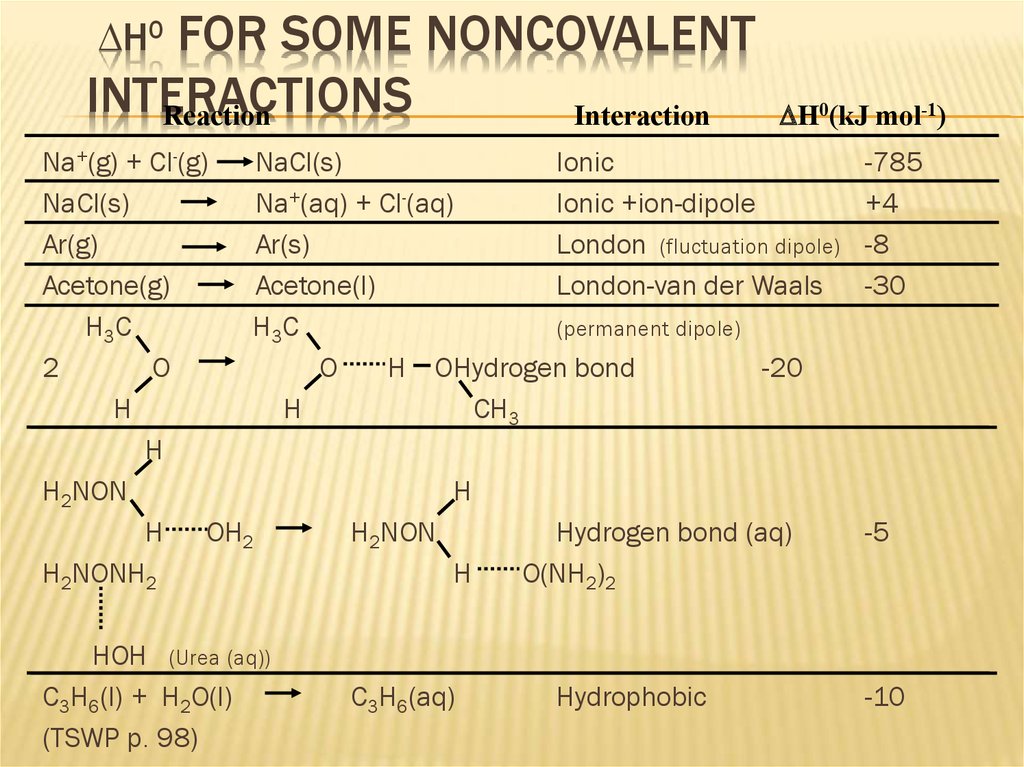
14. DH0 for some Noncovalent Interactions
FOR SOME NONCOVALENTINTERACTIONS
Reaction
Interaction
DH0
DH0(kJ mol-1)
Na+(g) + Cl-(g)
NaCl(s)
Ionic
NaCl(s)
Na+(aq) + Cl-(aq)
Ionic +ion-dipole
Ar(g)
Ar(s)
London (fluctuation dipole)
Acetone(g)
Acetone(l)
London-van der Waals
H3C
H3C
(permanent dipole)
2
O
O
H OHydrogen bond
-20
H
H
CH3
H
H2NON
H
H OH2
H2NON
Hydrogen bond (aq)
H2NONH2
H
O(NH2)2
HOH (Urea (aq))
C3H6(l) + H2O(l)
(TSWP p. 98)
C3H6(aq)
Hydrophobic
-785
+4
-8
-30
-5
-10
15. Protein Unfolding
PROTEIN UNFOLDINGProteins have a native state. (Really, they tend to have a tight cluster of native
states.)
Denaturation occurs when heat or denaturants such as guanidine, urea or detergent
are added to solution. Also, the pH can affect folding.
When performing a denaturation process non-covalent interactions are broken.
Ionic, van der-Waals, dipolar, hydrogen bonding, etc.
Solvent is reorganized.
16. Protein Unfolding
PROTEIN UNFOLDINGheat
Let’s consider denaturation with heat. We can determine a great deal about the
nature of the protein from such a consideration.
The experimental technique we use for measuring thermodynamic changes here is
the differential scanning calorimeter.
Basic experiment: Add heat to sample, measure its temperature change.
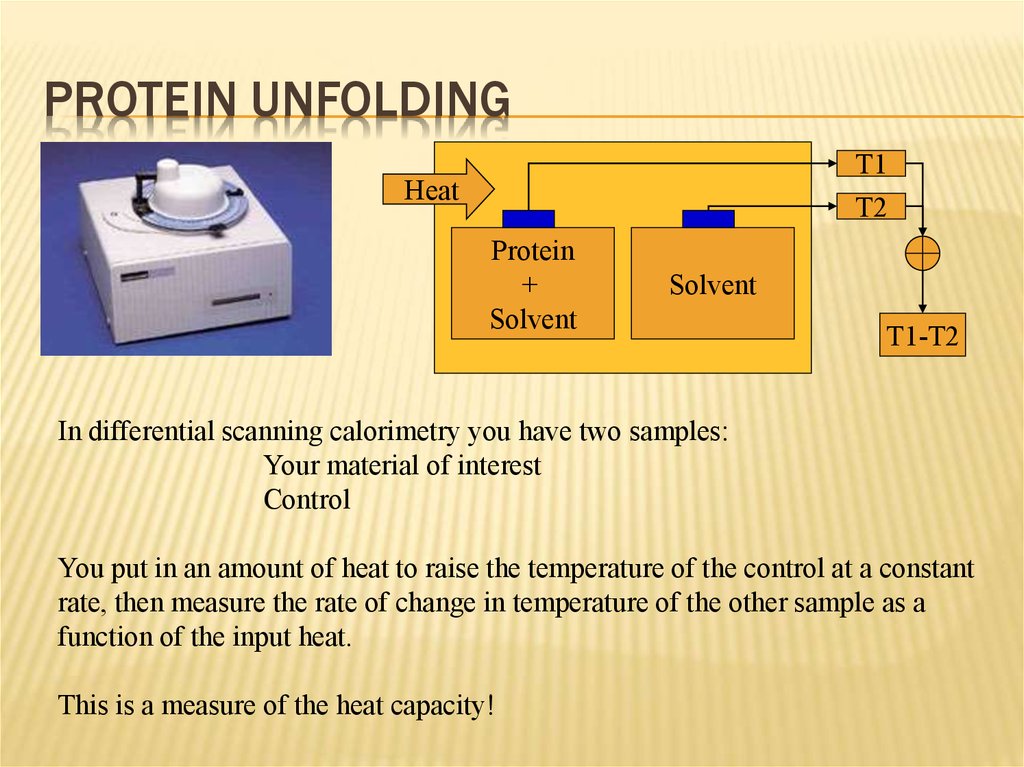
17. Protein Unfolding
PROTEIN UNFOLDINGT1
T2
Heat
Protein
+
Solvent
Solvent
T1-T2
In differential scanning calorimetry you have two samples:
Your material of interest
Control
You put in an amount of heat to raise the temperature of the control at a constant
rate, then measure the rate of change in temperature of the other sample as a
function of the input heat.
This is a measure of the heat capacity!
18. Protein Unfolding
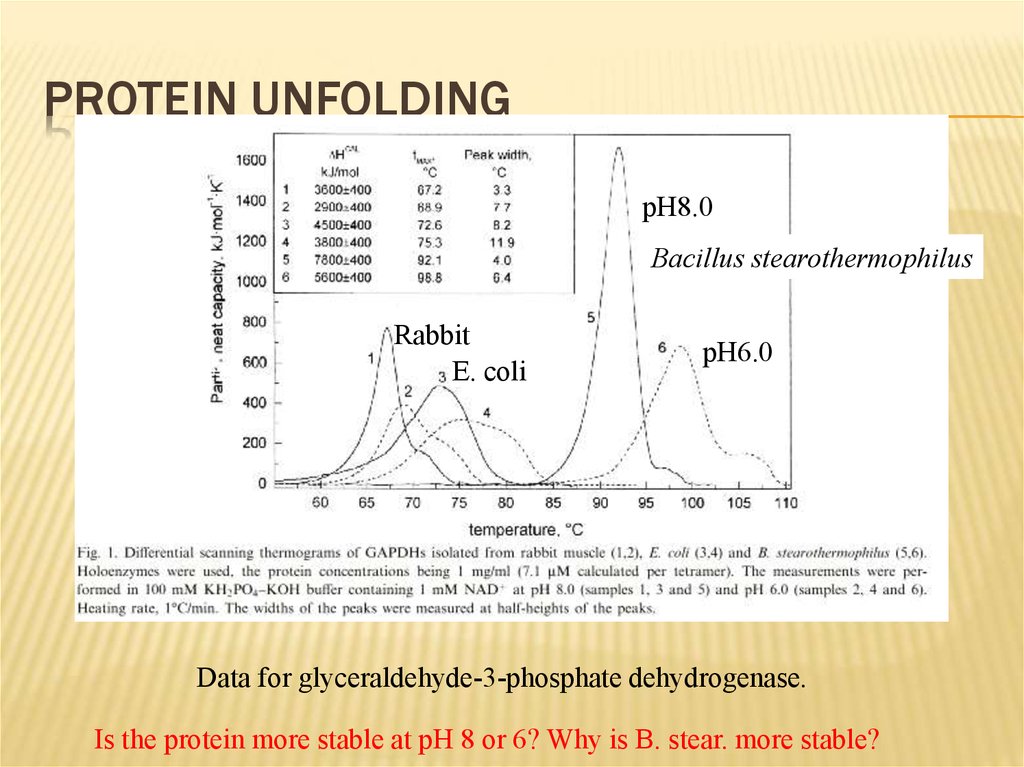
PROTEIN UNFOLDINGpH8.0
Bacillus stearothermophilus
Rabbit
E. coli
pH6.0
Data for glyceraldehyde-3-phosphate dehydrogenase.
Is the protein more stable at pH 8 or 6? Why is B. stear. more stable?
19. Protein Unfolding
PROTEIN UNFOLDINGWe are given the following data for the denaturation of lysozyme:
DG° kJ/mol
DH° kJ/mol
DS° J/ K mol
TDS° kJ/mol
10
25
60
100
67.4
137
297
69.9
60.7
236
586
175
27.8
469
1318
439
-41.4
732
2067
771
°C
Where is the denaturation temperature?
What then is special about the temperature at which the denaturation is spontaneous?















 chemistry
chemistry