Similar presentations:
Простые проценты. Наращение и дисконтирование. Лекция 1
1. Лекция 1
ПРОСТЫЕ ПРОЦЕНТЫ.Наращение и
дисконтирование
2. Обозначения
Лекция 1. ПРОСТЫЕ ПРОЦ
ЕНТЫ
I — проценты за весь срок ссуды;
Р — первоначальная сумма долга;
S — наращенная сумма, т. е. сумма в
конце срока;
i — ставка наращения процентов;
n — срок ссуды.
2
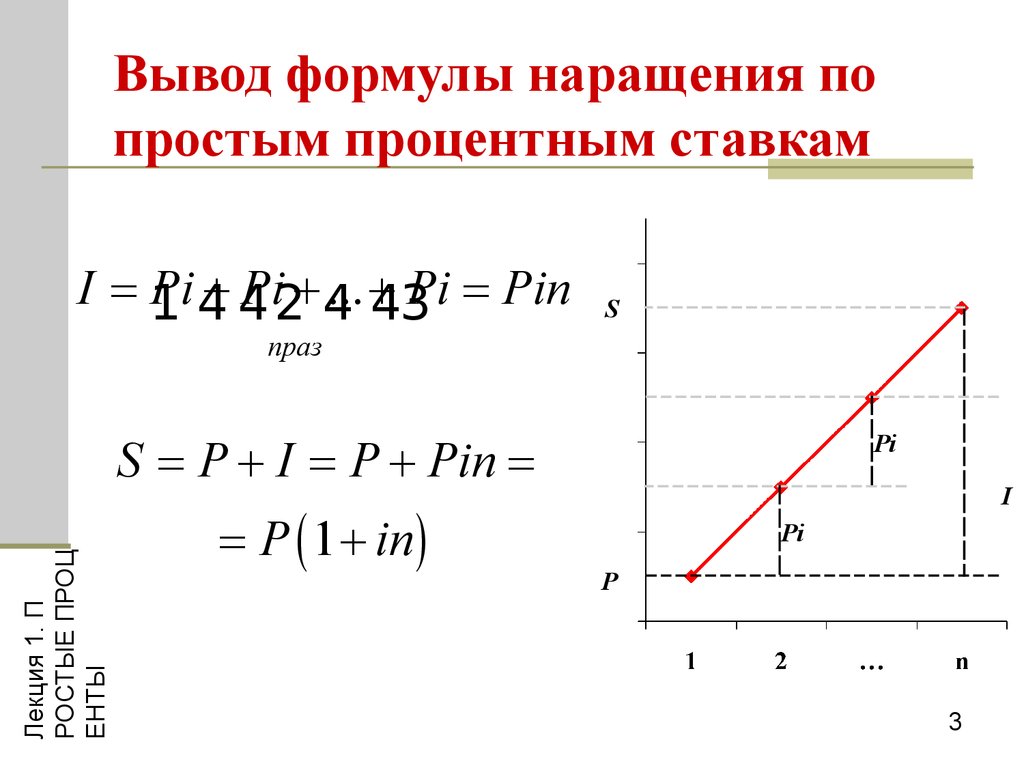
3. Вывод формулы наращения по простым процентным ставкам
I =1Pi 4
+4
Pi2+ 4
... +
Pi = Pin
43
S
nраз
Лекция 1. П
РОСТЫЕ ПРОЦ
ЕНТЫ
S = P + I = P + Pin =
= P ( 1 + in )
Pi
I
Pi
P
3
4. Практика расчета процентов для краткосрочных ссуд
Выразим срок ссуды n в виде дробиЛекция 1. П
РОСТЫЕ ПРОЦ
ЕНТЫ
t
n=
K
,
где t — число дней ссуды,
К — число дней в году, или временная база
начисления процентов.
4
5. Виды временной базы
Лекция 1. ПРОСТЫЕ ПРОЦ
ЕНТЫ
Германская система: К = 360 дней
(12 месяцев по 30 дней в каждом месяце);
Французская система: К = 360 дней
(12 месяцев с номинальным количеством
дней в каждом месяце);
Английская система: К = 365 (366) дней
(12 месяцев с номинальным количеством
дней в каждом месяце).
Если К = 360, то получают обыкновенные
или коммерческие проценты.
Если К = 365 (366) рассчитывают точные
5
проценты.
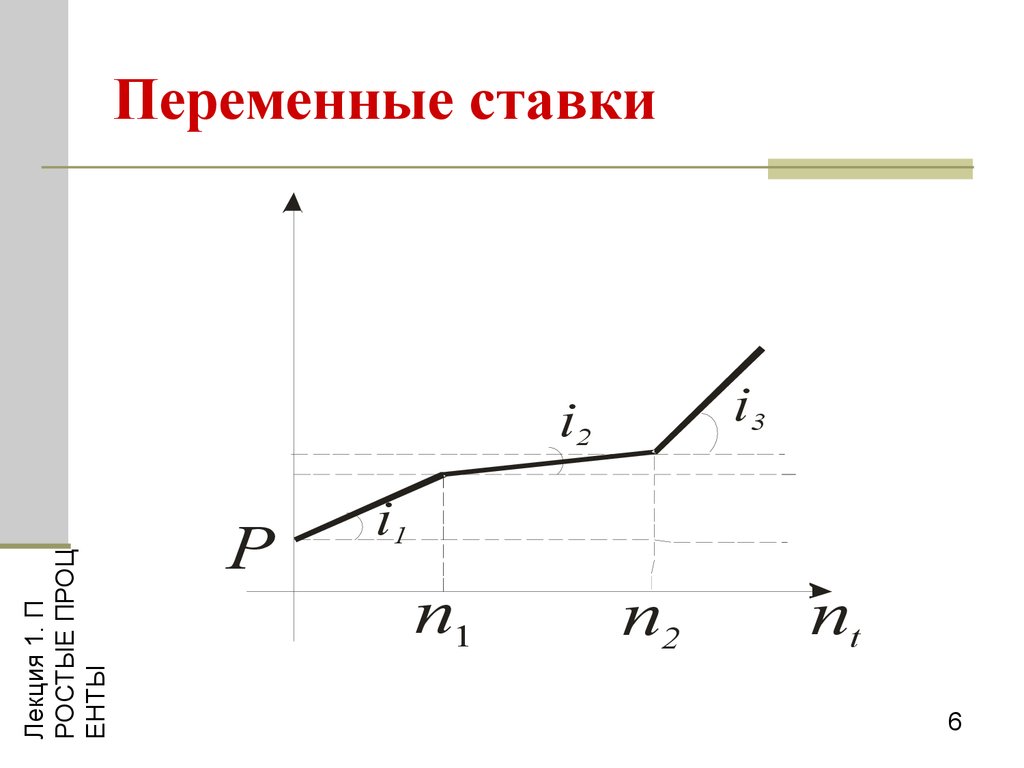
6. Переменные ставки
i3Лекция 1. П
РОСТЫЕ ПРОЦ
ЕНТЫ
i2
P
i1
n1
n2
nt
6
7. Переменные ставки
В случае если процентные ставки простые, тонаращенная на конец срока сумма определяется
следующим образом:
S = P ( 1 + n1i1 + n2i2 + L + nmim ) =
Лекция 1. П
РОСТЫЕ ПРОЦ
ЕНТЫ
æ
ö
= P ç1 + å nt it ÷
t
è
ø
где it - ставка простых процентов в периоде t,
nt - продолжительность периода с постоянной
ставкой
n = å nt
t
7
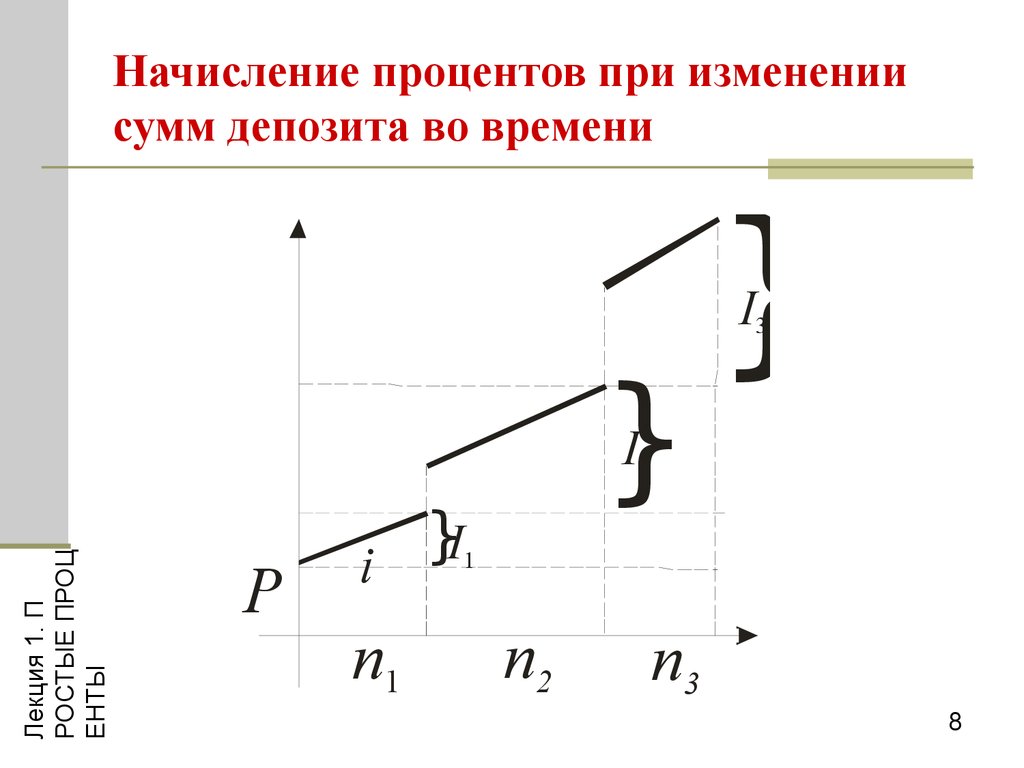
8. Начисление процентов при изменении сумм депозита во времени
}I3
}
Лекция 1. П
РОСТЫЕ ПРОЦ
ЕНТЫ
I2
P
}
I
i
1
n1
n2
n3
8
9. Начисление процентов при изменении сумм депозита во времени
Лекция 1. ПРОСТЫЕ ПРОЦ
ЕНТЫ
Пусть Rj - остаток средств на счете в момент j
после очередного поступления или списания
средств,
nj - срок хранения денег (в годах) до нового
изменения остатка средств на счете.
Тогда суммарные проценты за весь срок
финансовой операции будут равны
I = å I j = å R j n ji
j
j
9
10. Начисление процентов при изменении сумм депозита во времени
период nt, через который происходитизменение остатка на счете, не совпадает с
периодом
начисления
процентов,
следует
произвести пересчет процентной ставки, т.е.
Если
Rt
å
I = åR n i =
j j
j
Лекция 1. П
РОСТЫЕ ПРОЦ
ЕНТЫ
j
j
100
K
:
i
K означает число дней в году, а tj — срок в днях
между последовательными изменениями остатков
на счете.
10
11. Реинвестирование по простым ставкам
Наращеннаясумма для
реинвестировании составит
всего
срока
при
S = P(1 + n1i1 )(1 + n2i2 ) (1 + nt it )
Лекция 1. П
РОСТЫЕ ПРОЦ
ЕНТЫ
it — размер ставок, по которым производится
реинвестирование.
Если промежуточные сроки начисления и ставки
не изменяются во времени, то имеем
S = P(1 + ni )
m
т — количество повторений реинвестирования.
11
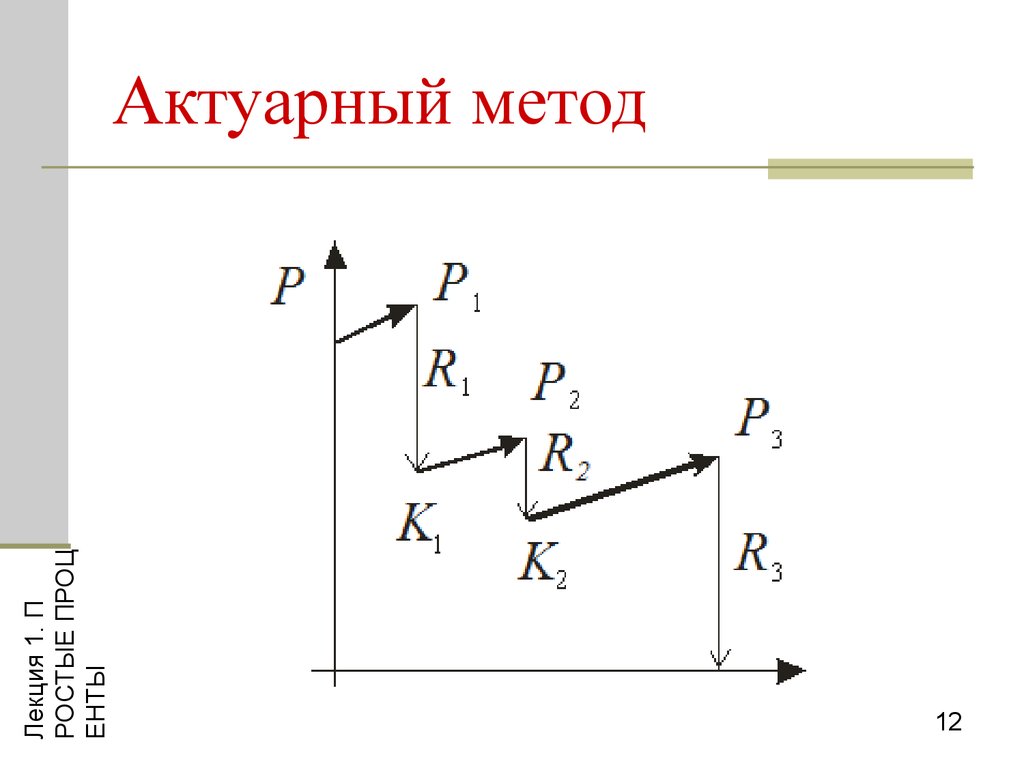
12. Актуарный метод
Лекция 1. ПРОСТЫЕ ПРОЦ
ЕНТЫ
Актуарный метод
12
13.
Формуладля
задолженности (Кj)
определения
остатка
K1 = P(1 + t1i ) R1
K 2 = K1 (1 + t 2i ) R2
Лекция 1. П
РОСТЫЕ ПРОЦ
ЕНТЫ
Задолженность на конец срока должна быть
полностью погашена, т.е.
K 2 (1 + t3i ) R3 = 0
13
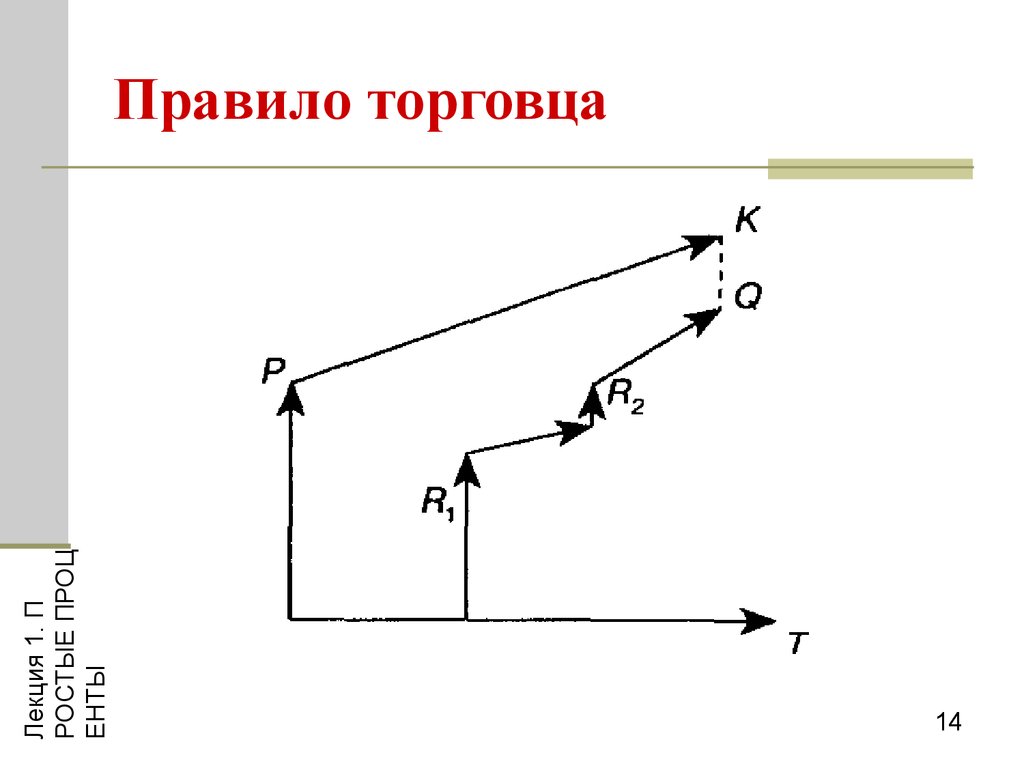
14. Правило торговца
Лекция 1. ПРОСТЫЕ ПРОЦ
ЕНТЫ
Правило торговца
14
15. Правило торговца
Лекция 1. ПРОСТЫЕ ПРОЦ
ЕНТЫ
Q = S K = P (1 + ni ) å R j (1 + t j i j )
где
Q — остаток долга на конец срока или года,
S — наращенная сумма долга,
K — наращенная сумма платежей,
Rj — сумма частичного платежа,
n — общий срок ссуды,
tj — интервал времени от момента платежа до
конца срока ссуды или года.
15
16. Наращение процентов в потребительском кредите
Наращенная сумма долгаS = P(1 + ni )
Величина
Лекция 1. П
РОСТЫЕ ПРОЦ
ЕНТЫ
составляет
разового
погасительного
платежа
S
R=
n m
n – срок кредита в годах
m – число платежей в году
16
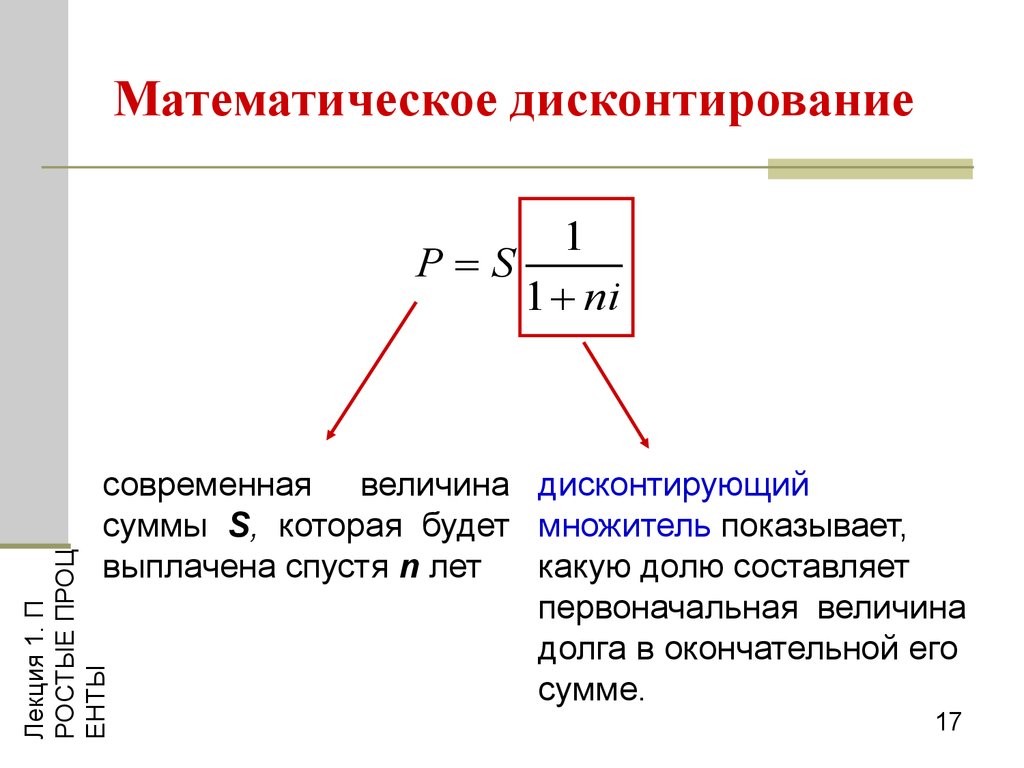
17. Математическое дисконтирование
1P=S
1 + ni
Лекция 1. П
РОСТЫЕ ПРОЦ
ЕНТЫ
современная величина дисконтирующий
суммы S, которая будет множитель показывает,
выплачена спустя n лет
какую долю составляет
первоначальная величина
долга в окончательной его
сумме.
17
18. Банковский учет (учет векселей)
Лекция 1. ПРОСТЫЕ ПРОЦ
ЕНТЫ
Банковский учет (учет векселей)
Размер дисконта, или суммы учета равен Snd; если
d — годовая учетная ставка, то n измеряется в
годах.
Р = S – Snd = S(1 - nd),
где п — срок от момента учета до даты погашения
векселя.
Дисконтный множитель равен (1 - nd).
При этом используется французская система
подсчета срока начисления процентов.
18
19. Наращение по учетной ставке
Простая учетная ставка иногда применяется приЛекция 1. П
РОСТЫЕ ПРОЦ
ЕНТЫ
расчете наращенной суммы: в этом возникает
необходимость при определении суммы, которую
надо проставить в векселе, если задана текущая
сумма долга.
Наращенная сумма в этом случае
1
S=P
1 nd
19
20. Срок ссуды
Из формул наращениявыразим п срок в годах.
Лекция 1. П
РОСТЫЕ ПРОЦ
ЕНТЫ
S P
n=
=
Pi
и
S
дисконтирования
1
P ,
i
P
1
S P
S.
n=
=
Sd
d
20
21. Величина процентной ставки
Изформул наращения и дисконтирования
выразим i или d, и получим выражения для
сроков, измеренных в годах и днях:
Лекция 1. П
РОСТЫЕ ПРОЦ
ЕНТЫ
S P S P
i=
=
K,
Pn
Pt
S P S P
d=
=
K.
Sn
St
n = t / K, где K – временная база
21















 finance
finance








