Similar presentations:
Логические выражения и таблицы истинности
1. Логические выражения и таблицы истинности
Автор: Шуплецова Я.А., учитель информатики и ИКТ МКОУ СОШ с.Заево2. Логические выражения
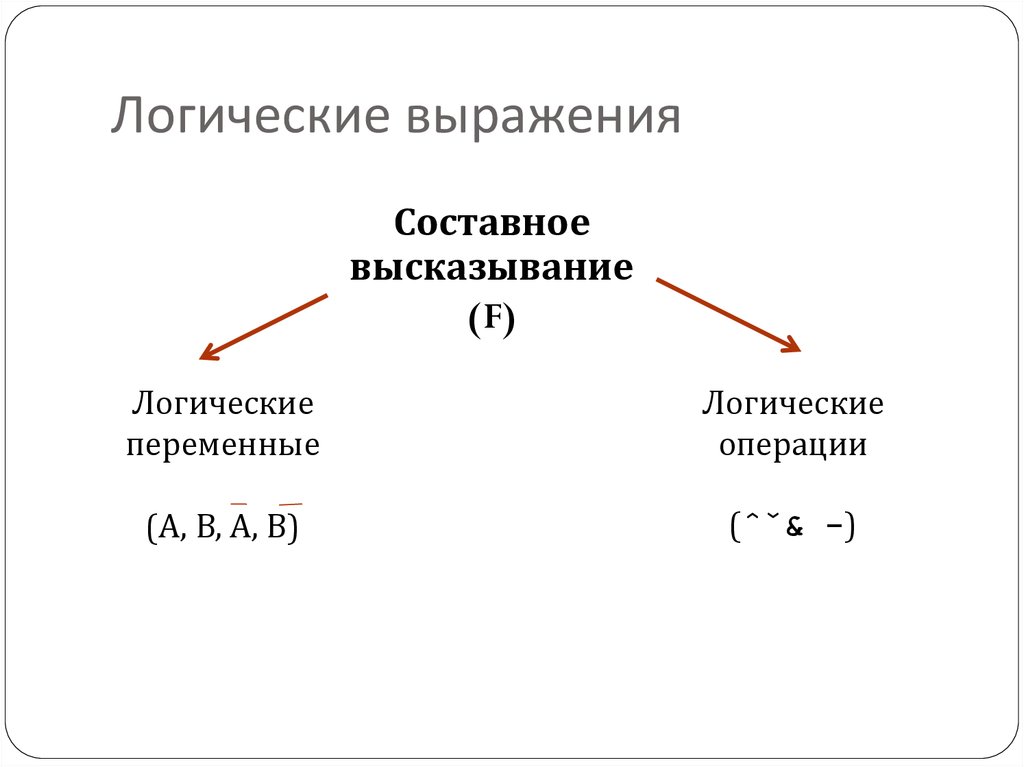
Составноевысказывание
(F)
Логические
переменные
Логические
операции
(А, В, А, В)
(ˆˇ& -)
3. Логические выражения
«(2*2 = 5 или 2*2 = 4)» и «(2*2=5 или 2*2 =4)»
А = «2*2 = 5» - ложно (0)
В = «2*2 = 4» - истинно (1)
«(А или В) и (А или В)»
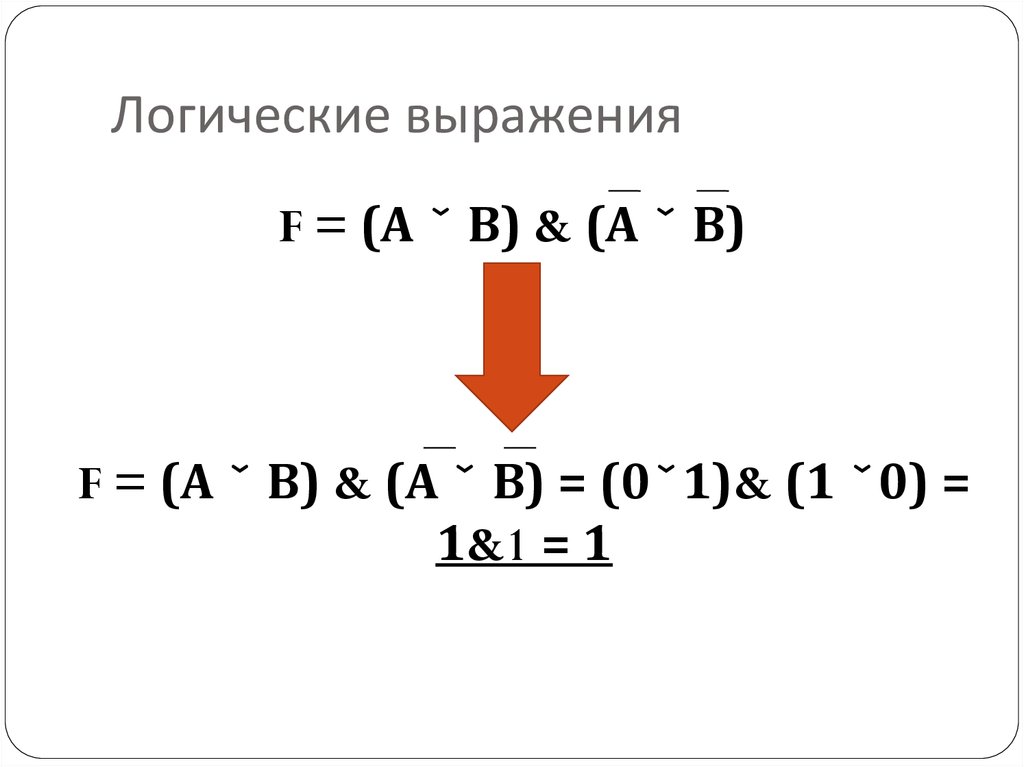
4. Логические выражения
F = (А ˇ В) & (А ˇ В)F = (А ˇ В) & (А ˇ В) = (0ˇ1)& (1 ˇ0) =
1&1 = 1
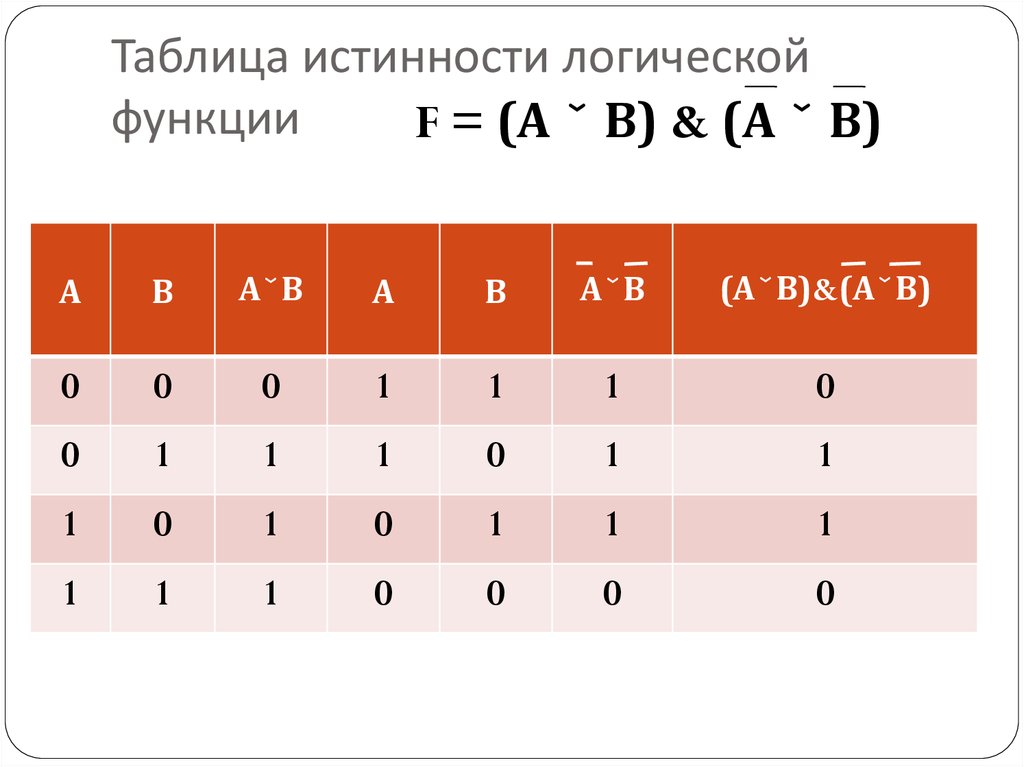
5. Таблица истинности логической функции
F = (А ˇ В) & (А ˇ В)А
В
АˇВ
А
В
АˇВ
(АˇВ)&(АˇВ)
0
0
0
1
1
1
0
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
6. Равносильные логические выражения
Логические выражения, у которых последниестолбцы истинности совпадают, называются
равносильными
«=»
Докажем,
что А & В и А ˇВ
равносильны
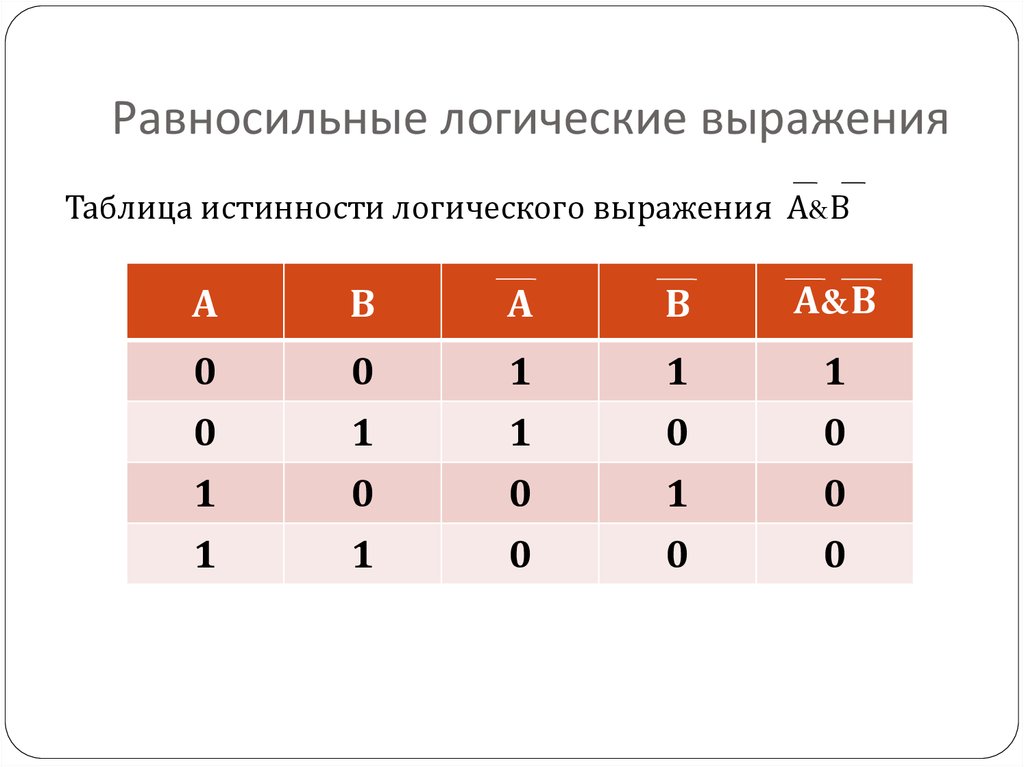
7. Равносильные логические выражения
Таблица истинности логического выражения А&ВА
В
А
В
А&В
0
0
1
1
1
0
1
1
0
0
1
0
0
1
0
1
1
0
0
0
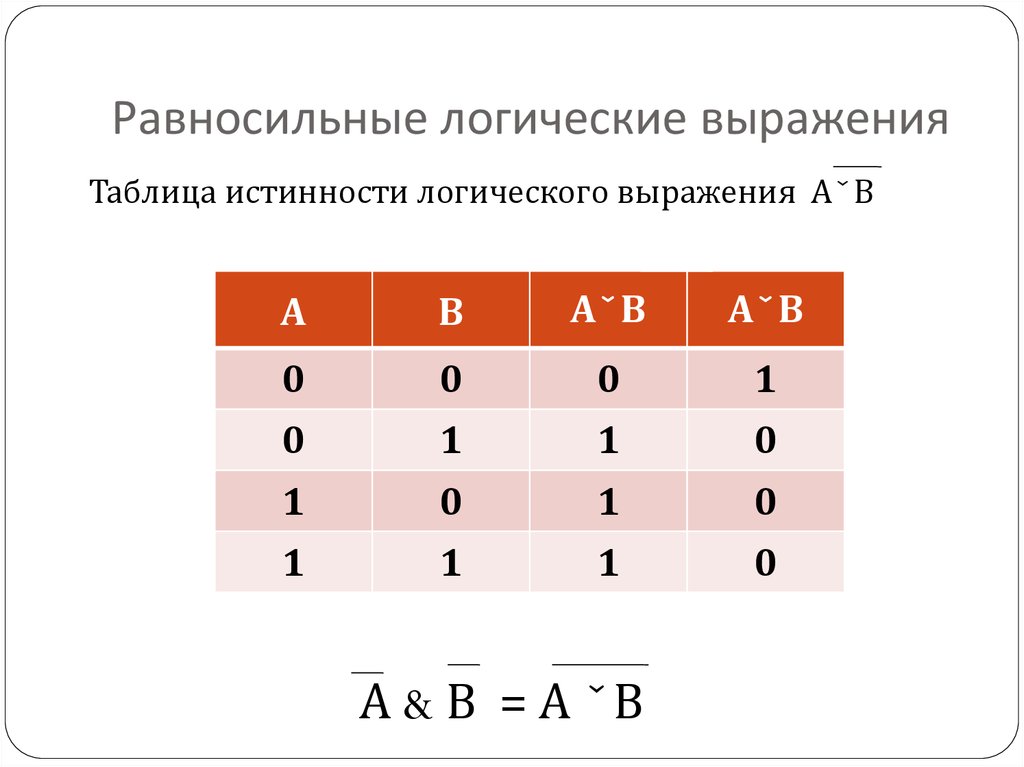
8. Равносильные логические выражения
Таблица истинности логического выражения АˇВА
В
АˇВ
АˇВ
0
0
0
1
0
1
1
0
1
0
1
0
1
1
1
0
А & В = А ˇВ
9. Домашнее задание
Задание №1Записать составное высказывание «(2*2=4 и 3*3 = 9)
или (2*2 = 4 и 3*3 = 9)» в форме логического
выражения. Построить таблицу истинности.
Задание №2
Доказать, используя таблицы истинности,
логические выражения АˇВ и А&В равносильны.
что




 informatics
informatics








