Similar presentations:
Теорема Виета. Развитие критического мышления школьников на уроке математики
1. РАЗВИТИЕ КРИТИЧЕСКОГО МЫШЛЕНИЯ ШКОЛЬНИКОВ НА УРОКЕ МАТЕМАТИКИ
2. Тема урока: «Теорема Виета».
3. Цели урока: • познакомить учащихся с теоремой Виета; • научить применять теорему Виета для составления квадратных уравнений; •
сформулировать теорему, обратнуютеореме Виета, и научить применять
ее к решению квадратных
уравнений.
4. Устная работа. 1. Назовите полные, неполные и приведённые квадратные уравнения: а) 3х2 – 2х = 0; б) 7х2 – 16х + 4 = 0; в) х2 –
3 = 0;г) –х2 + 2х – 4 = 0;
д) 2 – 6х + х2 = 0;
е) –21х2 + 16х = 0;
ж) х2 = 0;
з) х2 + 4х + 4 = 0;
и) х2 = 4;
к) –7х2 + 6 = 0.
5. 2. Преобразуйте квадратное уравнение в приведённое: а) 3х2 + 6х – 12 = 0; б) 2х2 = 0; в) –х2 – 2х + 16 = 0; г) х2 + х – 2 = 0;
д) 3х2 – 7 = 0;е) –5х2 + 10х – 2 = 0.
6. Объяснение нового материала
Уравнениех2 – 3х - 4 = 0
х2 – х – 12 = 0
х2 + 5х + 6 = 0
х2 + 3х – 10 = 0
х2 - 8х + 7= 0
х2 – 6х – 7 = 0
b
c
Корни
Сумма корней
Произведение корней
7. Рассмотреть доказательство теоремы можно как по учебнику (с. 127– 128), так и привлекая учащихся, поскольку оно не является
сложным.После доказательства на доску выносится
запись:
Теорема Виета
Если х1, х2 – корни уравнения
x2 + px + q = 0,
то х1 + х2 = –р;
х1 · х2 = q.
8. 2. Т е о р е м а В и е т а для неприведённого квадратного уравнения. 3. Т е о р е м а, обратная теореме Виета.
2. Т е о р е м а В и е т а для неприведённогоквадратного уравнения.
Теорема Виета
Если х1, х2 – корни уравнения
аx2 + bx + c = 0,
b
c a
то х1 + х2 =
х1 ∙ х2 =
a
;
.
3. Т е о р е м а, обратная теореме Виета.
9. 3. Педагогический эксперимент
10.
№ ФИОПонравился
вам Нравятся ли вам уроки Сможете ли вы самостоятельно
сегодняшний урок? математики?
выполнить
задания,
пройденные на уроках?
До
после
до
после
до
после
1
Бабкова В.
Да
Да
Да
Да
Да
Да
2
Балаян А.
Да
Да
Да
Да
Да
Да
3
Бахметьева П.
Да
Да
Нет
Да
Да
Да
4
Блудов А.
Да
Да
Да
Да
Да
Да
5
Гуреева С.
Да
Да
Нет
Да
Да
Да
6
Добрин Л.
Да
Да
Да
Да
Да
Да
7
Захарова М.
Да
Да
Да
Да
Да
Да
8
Зверев В.
Да
Да
Да
Да
Да
Да
9
Карапетян М..
Да
Да
Нет
Да
Нет
Да
10 Кирпанева А.
Да
Да
Да
Да
Да
Да
11.
Таблица 2. Своднаятаблица
Понравился вам Нравятся ли вам Сможете
ли
вы
сегодняшний
уроки математики? самостоятельно
урок?
выполнить……,
пройденные на уроках?
до
после
до
после
до
после
Да
23
26
17
23
19
26
Нет
4
1
10
4
8
1
12.
Процент времени активности =(А1 * (100%-Х1%)/100% + А2 * (100%Х2%)/100% + … + Ар * (100%-Хр%)/100%)
* K / 100%.
Где:
А1, А2, …, Ар – количество учеников в группе;
Х1, Х2, …, Хр – процент времени, который группа
учеников отвлекается от урока;
K – всего учеников в классе
13.
Процент времени активности обычныхуроков = (5*(100-10)/100 + 2*(10050)/100 + 20*(100-0)/100)*100/27 =
94,4%.
Процент времени активности во время
эксперимента = (1* (100-20)/100 + 26)
*100/27 = 99,3 %.
14.
Таблица 3. Результаты исследованияЭмоции Инте Качество
(%)
рес знаний,
(%) умений,
навыков
(%)
До
86
63
70
Пос
ле
96
86
96
Процент
времени
активности
учеников
(%)
94,4
99,3
15.
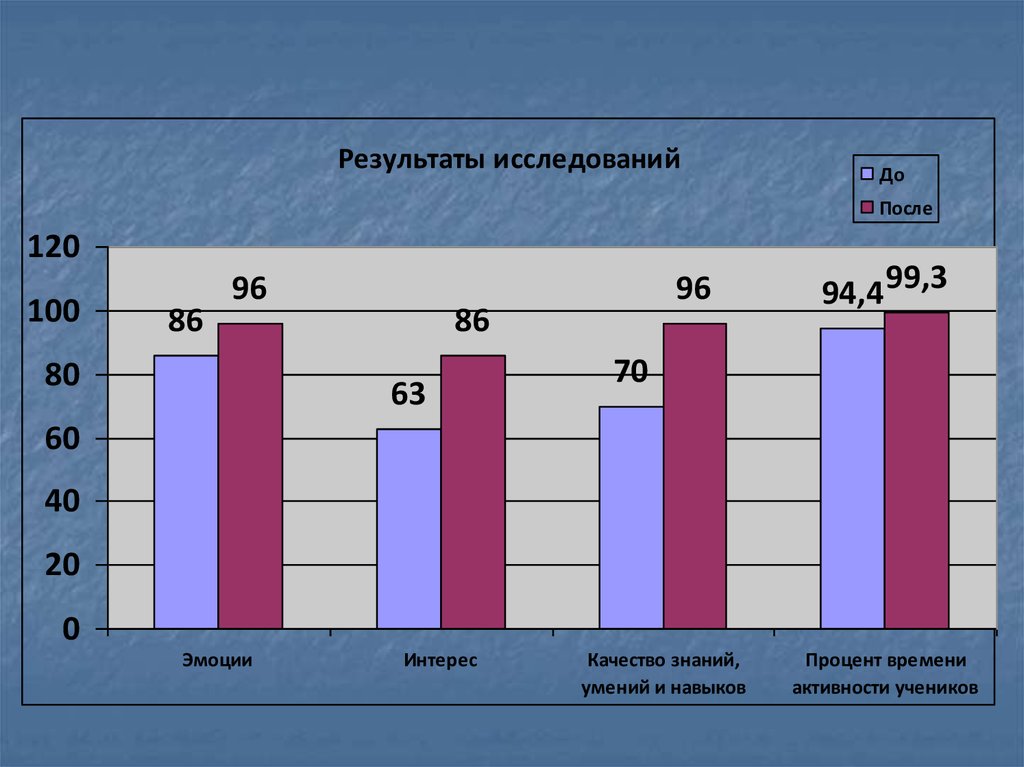
Результаты исследованийДо
После
120
100
86
96
80
96
86
63
94,4 99,3
70
60
40
20
0
Эмоции
Интерес
Качество знаний,
умений и навыков
Процент времени
активности учеников
16. Активность до эксперимента = (86+63+70+94,4)/4 = 78% Активность после эксперимента = (96+86+96+99,3)/4 = 94%
10090
80
70
60
50
40
30
20
10
0
94
78
Активность
класса до
эксперимента
Активность
класса после
эксперимента
















 mathematics
mathematics








