Свойства функции. Наибольшее и наименьшее значение функции

1. Тема урока

Свойства функции.
• Наибольшее и наименьшее значение
функции.
Разуму свойственно размышлять, то есть связывать
причины и следствия, давать ответ на вопрос «почему»,
выявлять случайное, обнаруживать закономерности, находить в
цепи происходящего начала и концы.
Ж.Фабр

2. Из истории

• Термин «функция» возник лишь в 1664 году
в работах немецкого ученого Лейбнеца,
только его ученик Бернулли в 1718 году дал
определение функции, свободное от
геометрических образов. Леонард Эйлер
определяет функцию так: «Величины,
зависящие от других так, что с изменением
вторых меняются и первые, называется
функцией».

3. Актуализация полученных знаний.

Фронтальная работа
• Функция называется возрастающей на
промежутке, если …,
• Функция называется убывающей на
промежутке, если ….
• Доказать , что функция является
возрастающей и построить график
у
х 2 1

4. ГИА

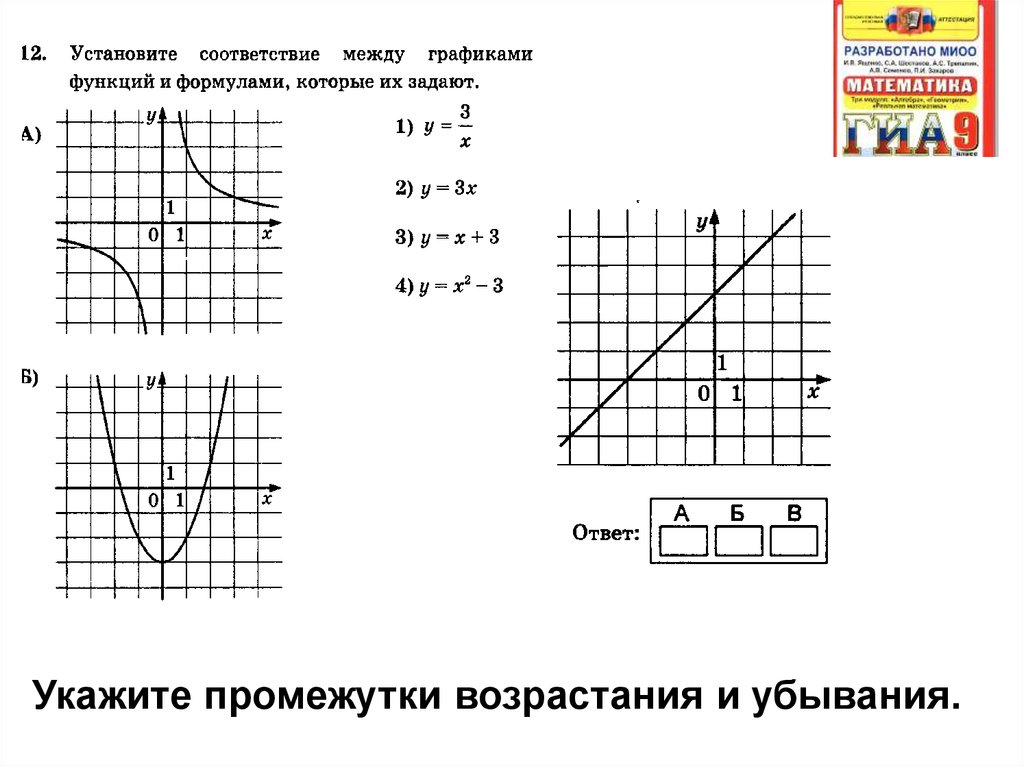
Укажите промежутки возрастания и убывания.

5. Установить соответствие ГИА

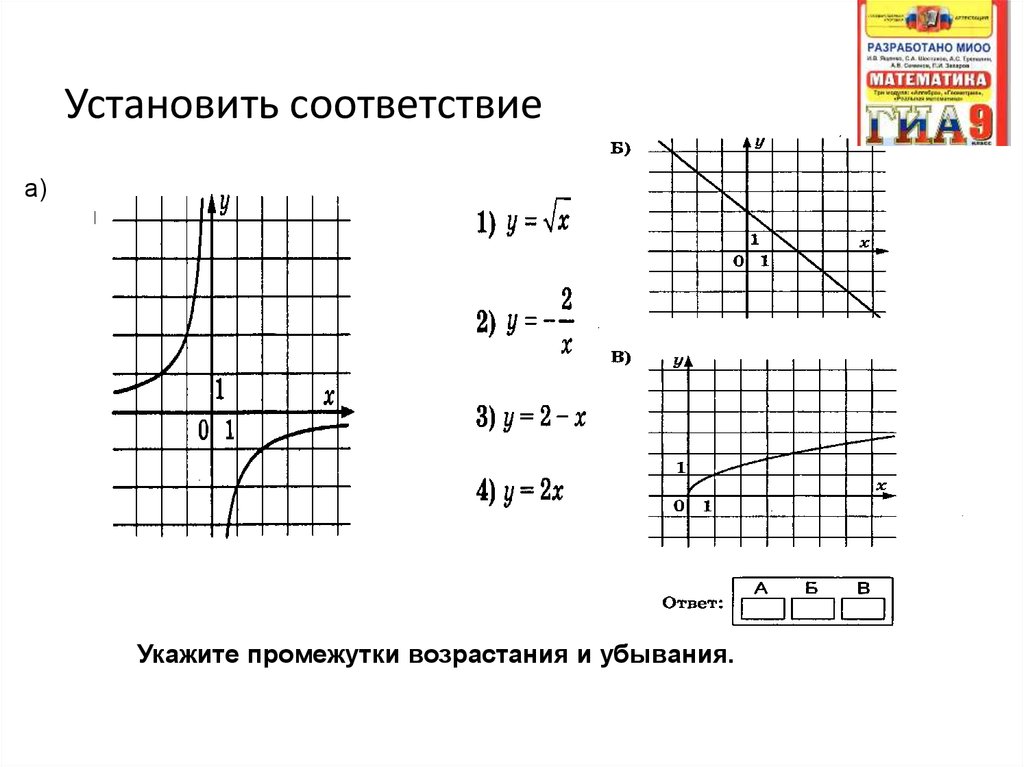
Установить соответствие
а)
Укажите промежутки возрастания и убывания.
ГИА

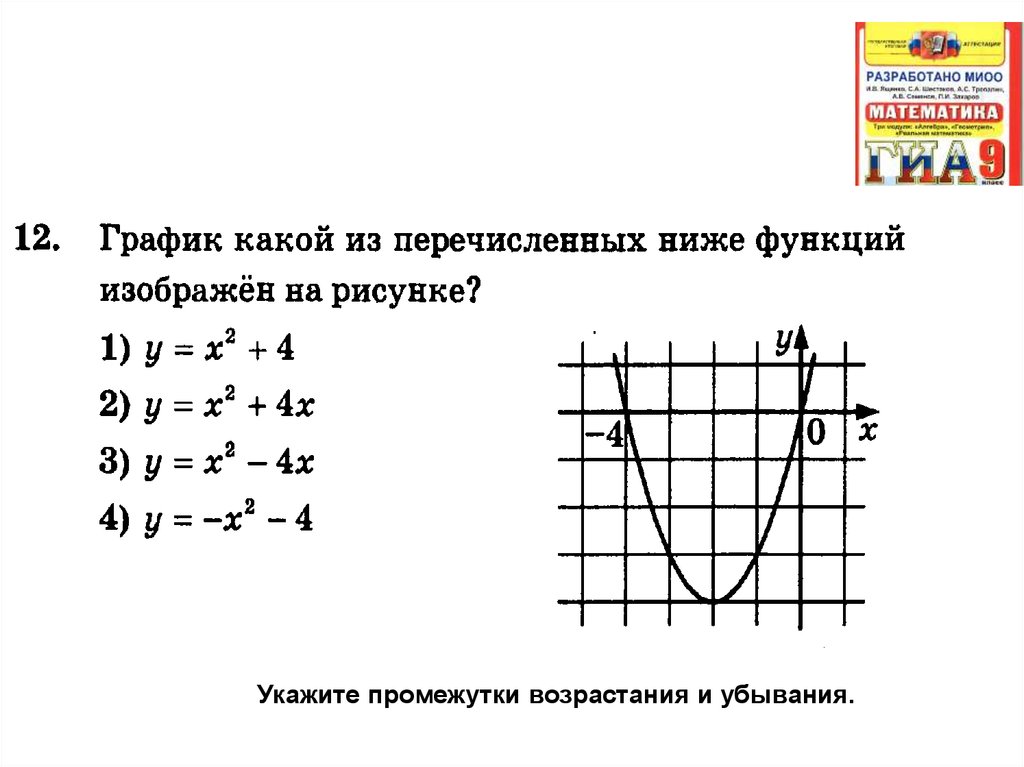
6. ГИА

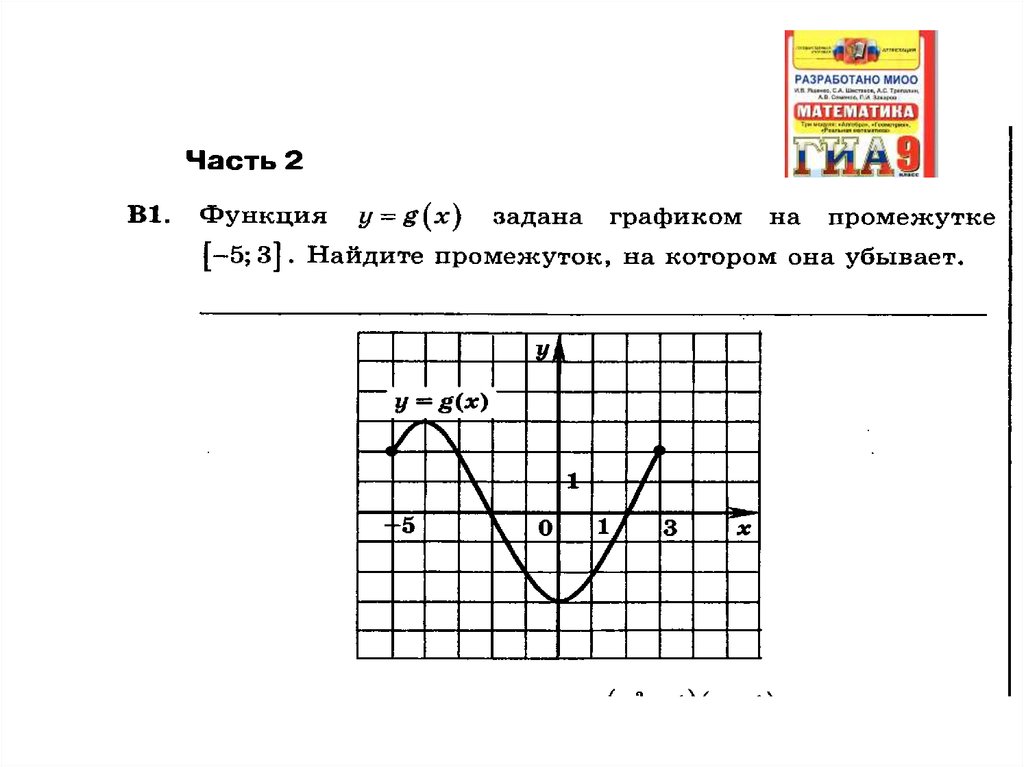
Укажите промежутки возрастания и убывания.

7. ГИА

8. ГИА

9. Работа в тетради и на доске

Построить графики функций,
найти область определения
промежутки возрастания,
промежутки убывания,

10. Изучение нового материала

• Какую функцию называют ограниченной
сверху, снизу?
• Что называют наименьшим , наибольшим
значением функции
• Повторение свойств выпуклости и
непрерывности.
• Стр 99-102( определения)

11.

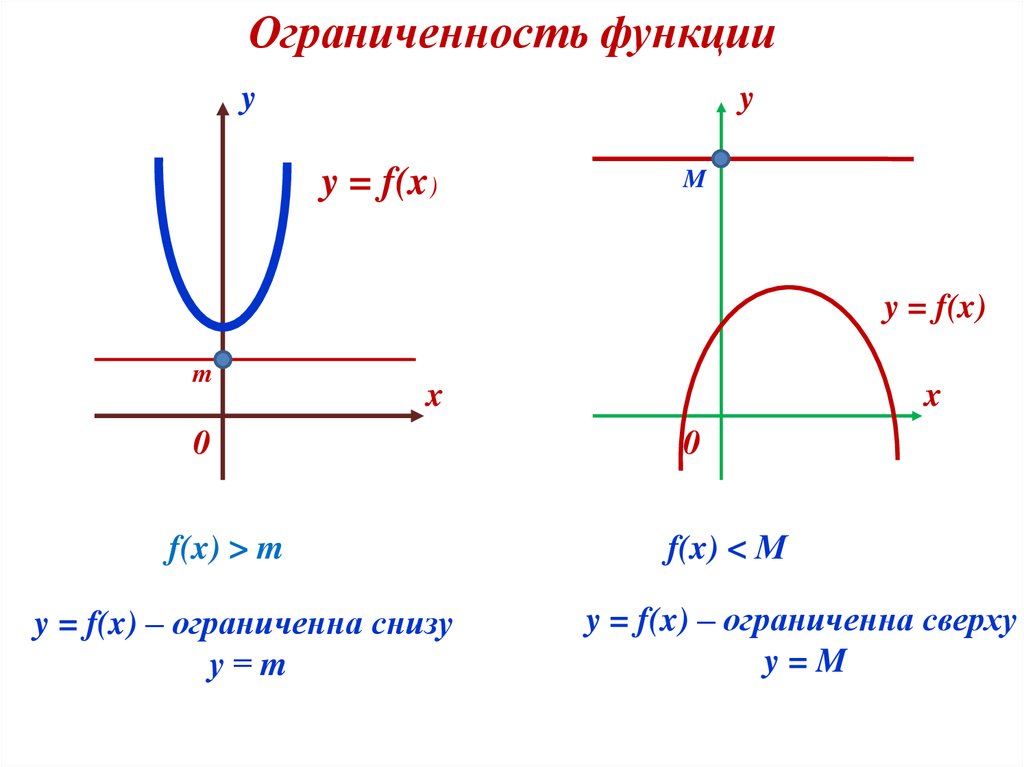
Ограниченность функции
y
y
y = f(x)
M
y = f(x)
m
x
0
f(x) > m
y = f(x) – ограниченна снизу
у=m
x
0
f(x) < М
y = f(x) – ограниченна сверху
y=M

12.

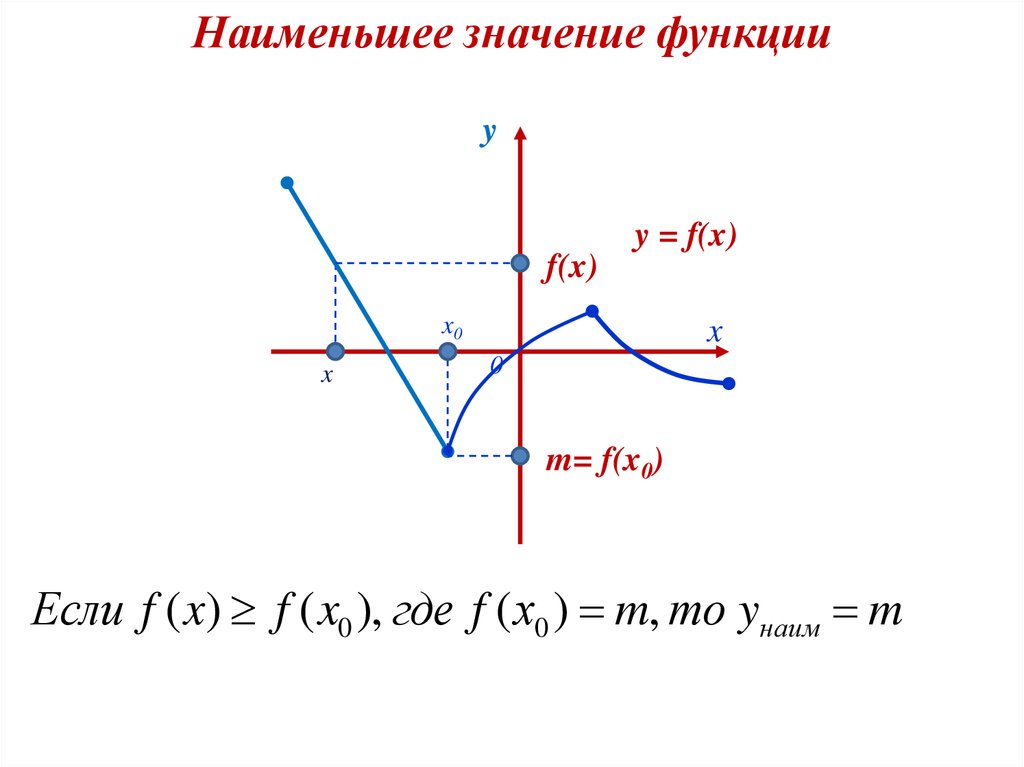
Наименьшее значение функции
y
y = f(x)
f(x)
x0
x
x
0
m= f(x0)
Если f ( x) f ( x0 ), где f ( х0 ) m, то yнаим m

13.

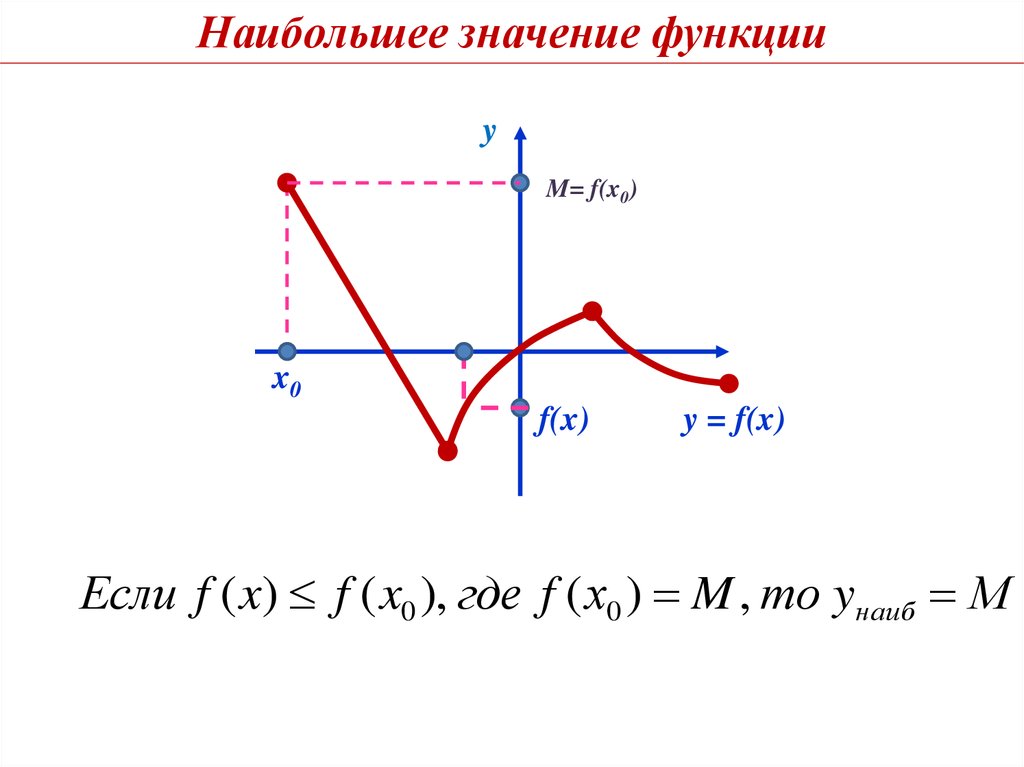
Наибольшее значение функции
y
M= f(x0)
x
x
0
x0
f(x)
y = f(x)
Если f ( x) f ( x0 ), где f ( х0 ) M , то yнаиб М

14. Верно ли высказывание?

Если у функции существует наименьшее значение, то
она ограничена снизу.
Если у функции существует наибольшее значение, т о
она ограничена сверху.
Если функция не ограничена снизу, то она не имеет
наименьшего значения.
Если функция не ограничена сверху, то она не имеет
наибольшего значения

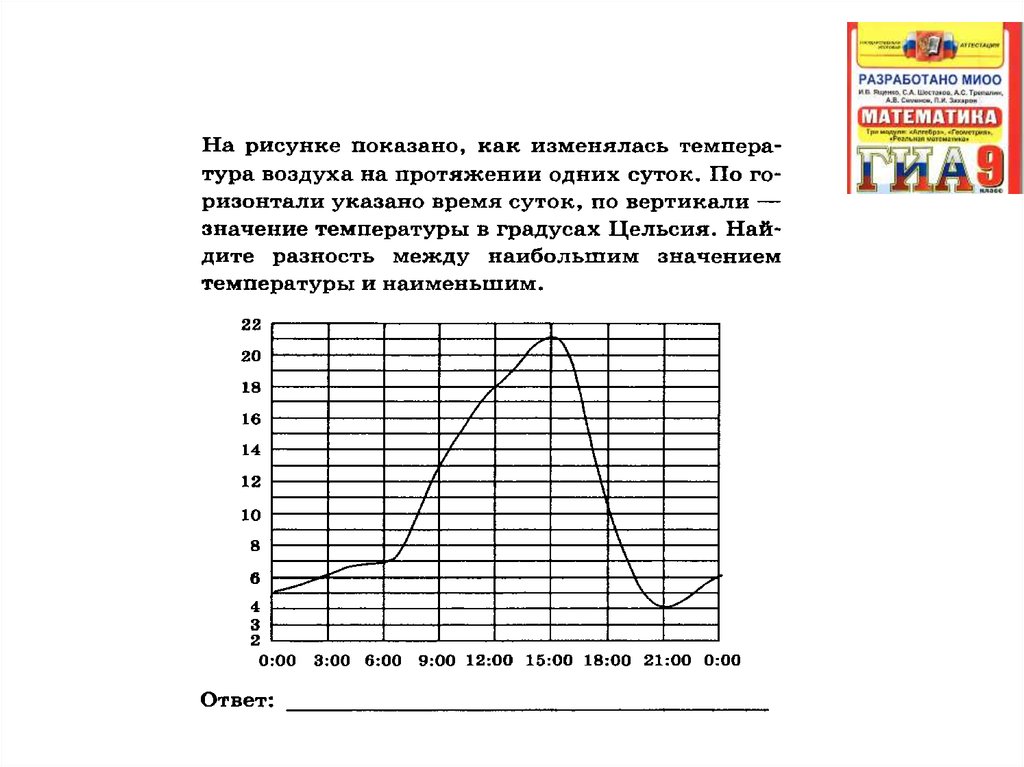
15. ГИА

16.

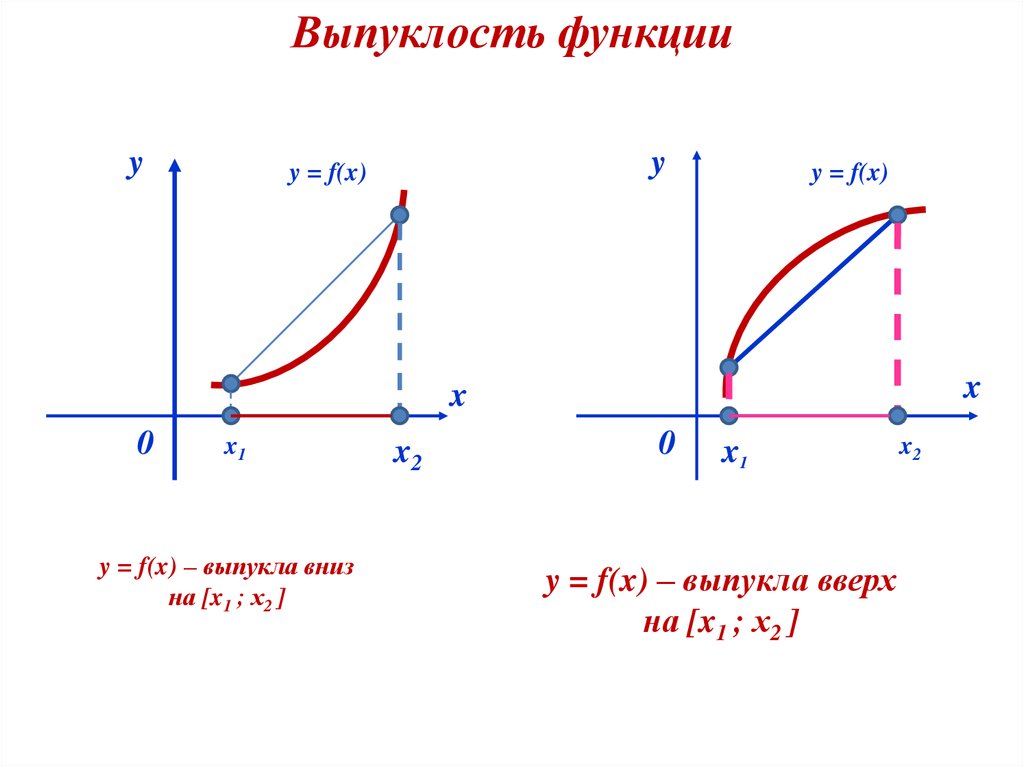
Выпуклость функции
y
y
y = f(x)
y = f(x)
x
x
0
x1
y = f(x) – выпукла вниз
на [x1 ; х2 ]
x2
0
x1
y = f(x) – выпукла вверх
на [x1 ; х2 ]
x2

17.

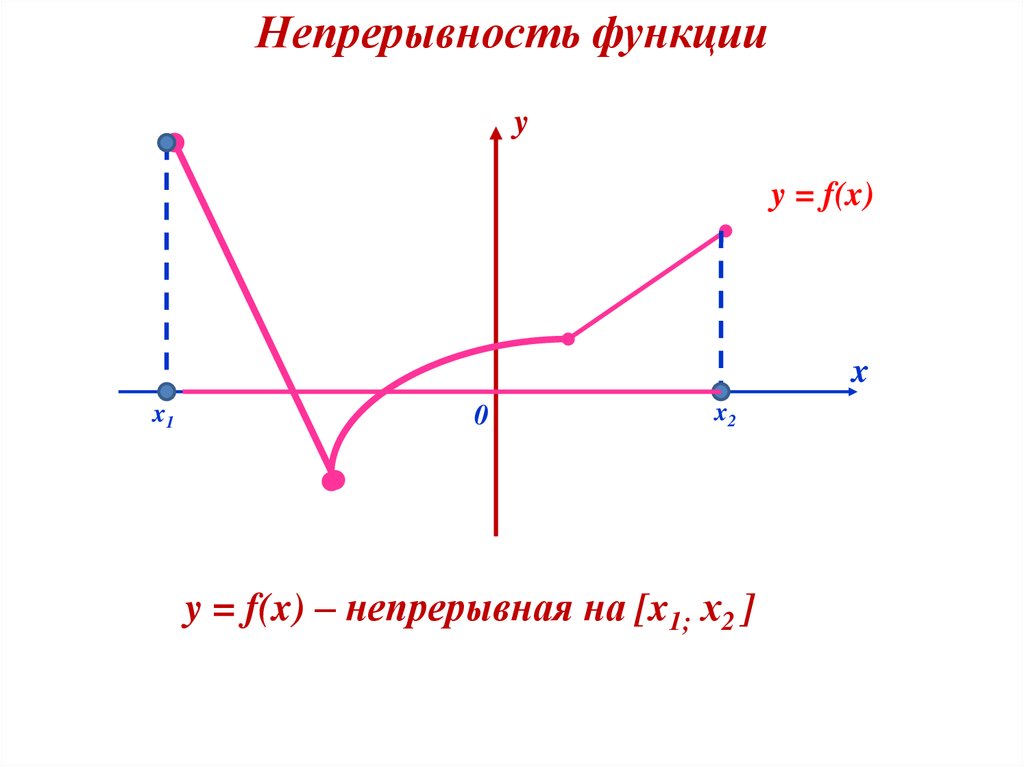
Непрерывность функции
y
y = f(x)
x
x1
0
x2
y = f(x) – непрерывная на [x1; х2 ]

18. Образцы решения примеров на нахождение наибольшего и наименьшего значений функции

19. Работа с эу

20. Задание на дом.

Параграф 10, упражнения
10.11(в),
10.13(в),
8.30(в)
Вариант 4 сборник ГИА

21. Работа с доской письменно

• Работа в тетрадях
• Самостоятельная работа из ресурсов ЭОР