Similar presentations:
Показательная функция
1. Презентация к уроку: «Показательная функция»
Выполнилаучитель математики
Бородина С. Ю.
МБОУ «СОШ №8»
Тбилисский район
Краснодарский край
2.
Показательнаяфункция
Некоторые наиболее часто
встречающиеся виды
трансцендентных функций, прежде
всего показательные, открывают
доступ ко многим исследованиям.
Л. Эйлер
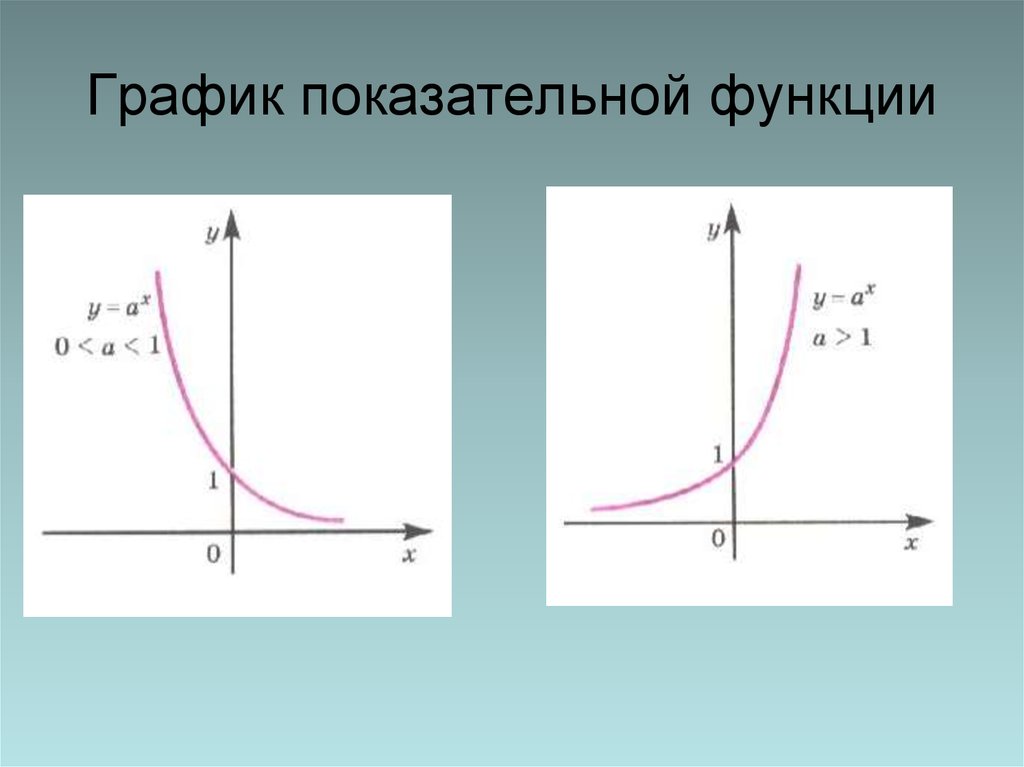
3. Определение. Показательной функцией называется функция y=ax, где а – заданное число, а>0, а≠1.
Определение.Показательной функцией
называется функция y=ax, где а –
заданное число, а>0, а≠1.
4. Свойства показательной функции
1. Область определения показательной функции – множество Rвсех действительных чисел.
2. Множество значений показательной функции – множество всех
положительных чисел.
3. Показательная функция y=ax является возрастающей на
множестве всех действительных чисел, если a>1, и
убывающей, если 0<a<1.
5. График показательной функции
6. Сравнение чисел
Сравните числа:а) 2π и 23,14.
Решение.
Так как π>3,14 и у=2х возрастает на R,
то 2π>23,14.
1
3
2
1
3
3
б)
и
.
Решение.
Так как 2 <
то 1 1
2
3
3
3
3 и
1
y
3
x
убывает на R,
7.
8.
9. Методы решения показательных уравнений
1.Ответ x= -3
10.
2.11.
3.12.
4.13.
5.14.
6.15.
7.16.
8.17. Решение простейших показательных неравенств
aЕсли а>1, то
f x g x
f x
a
g x
Если 0<а<1, то
f x g x

















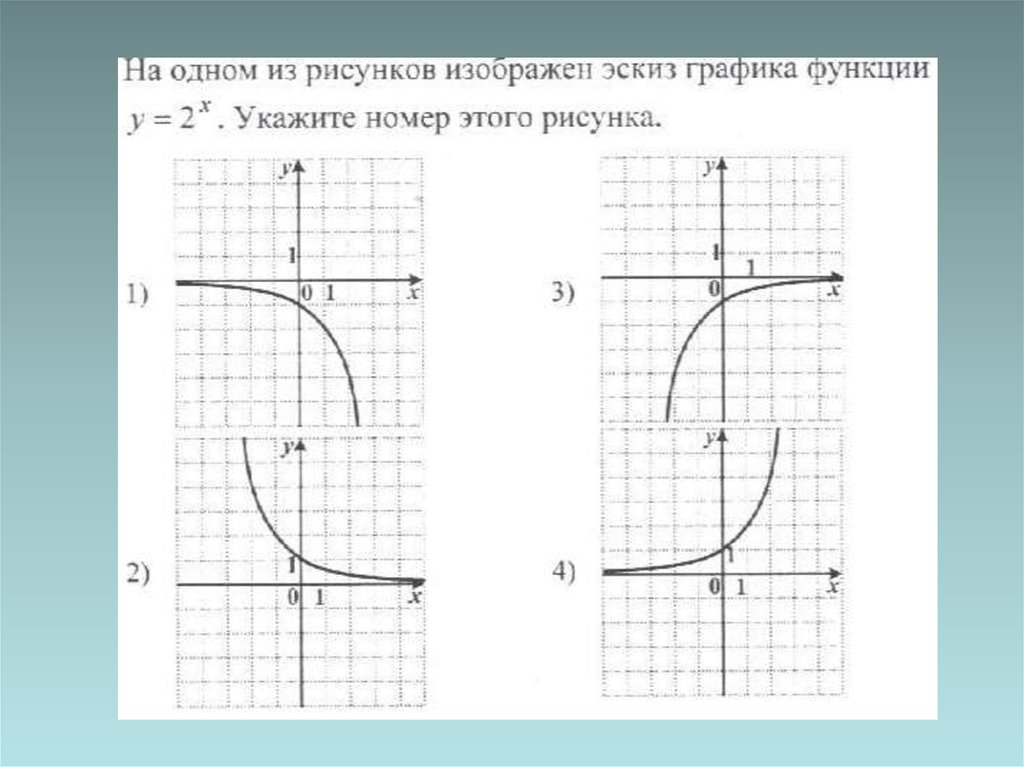
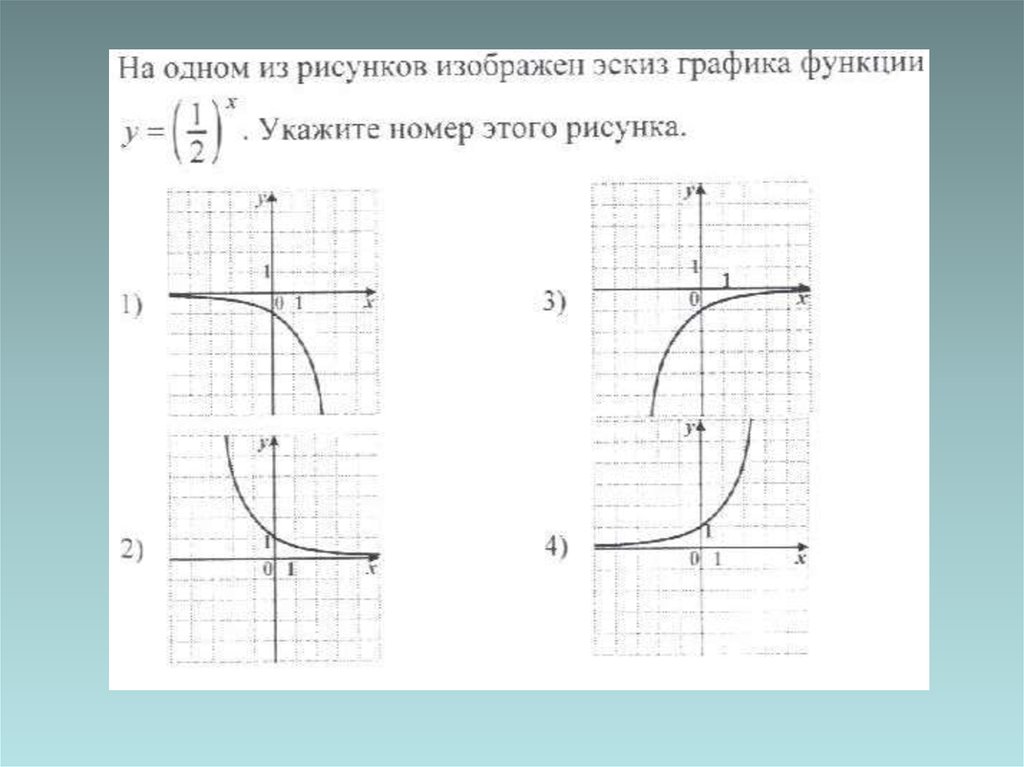
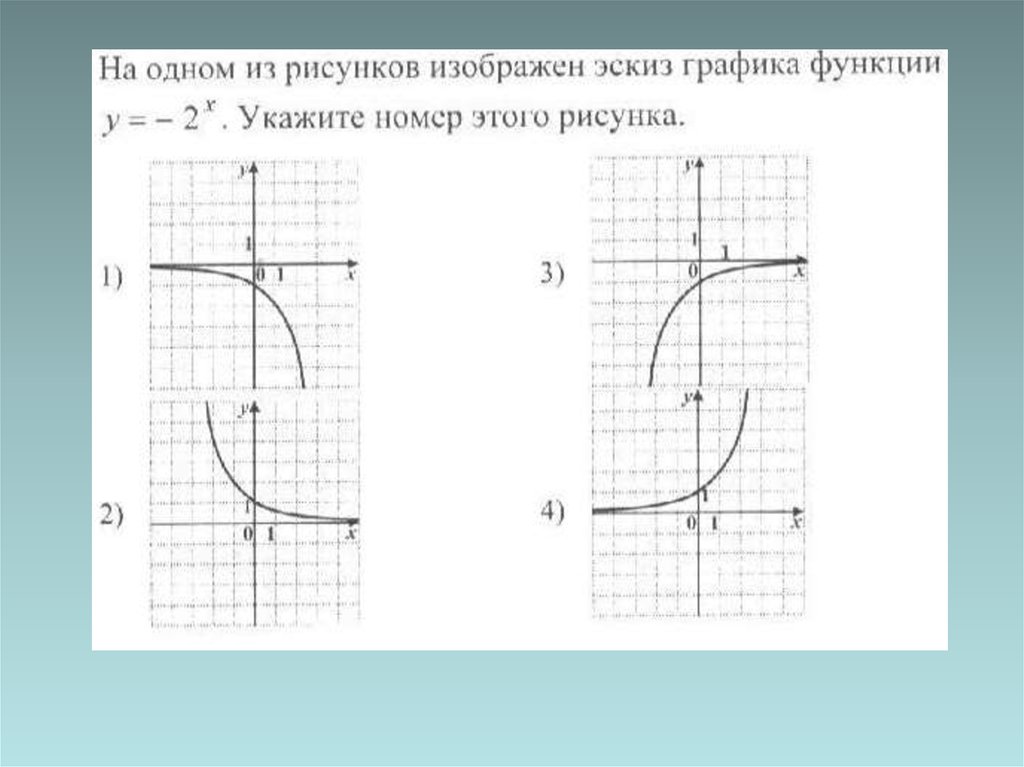
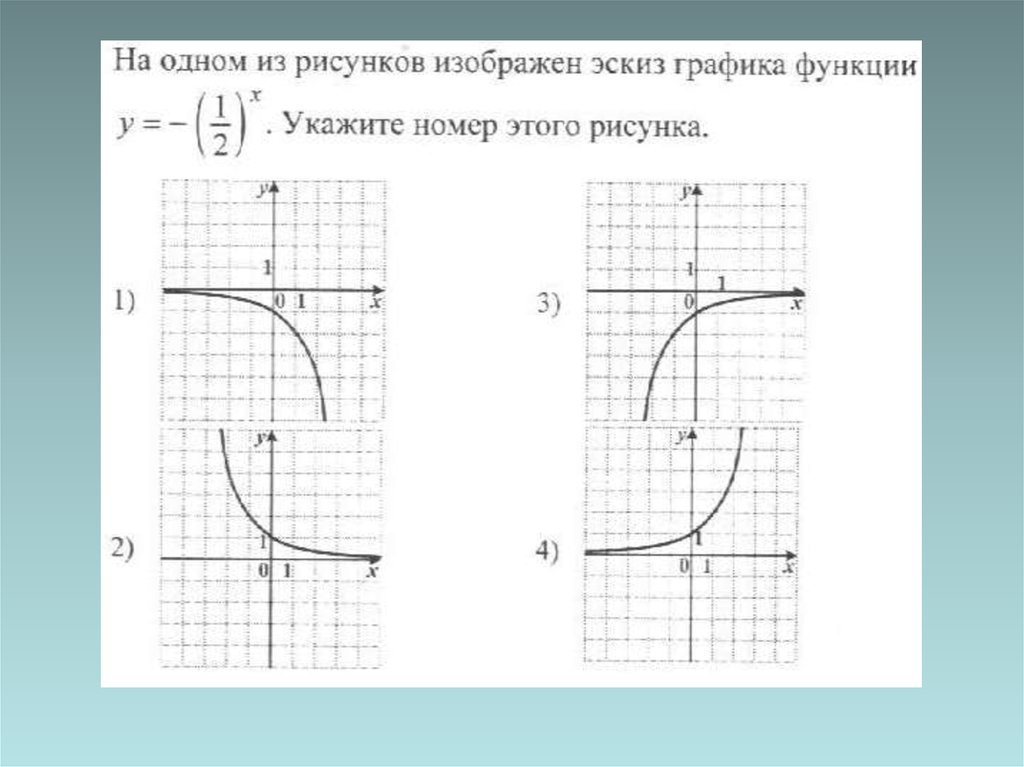
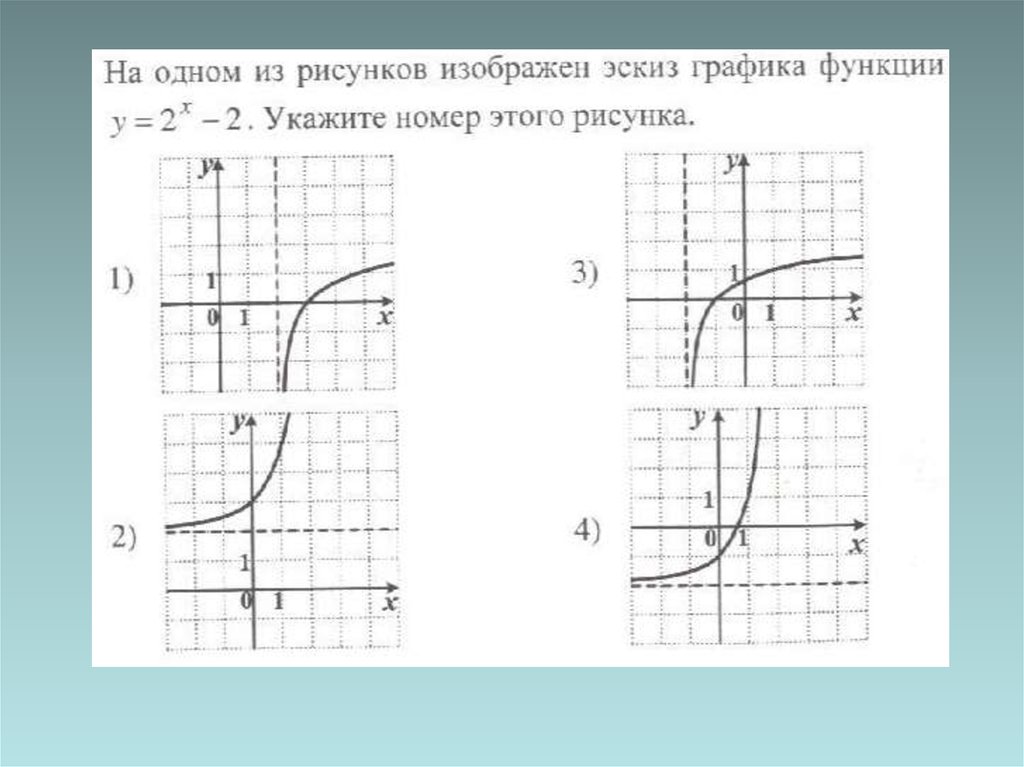
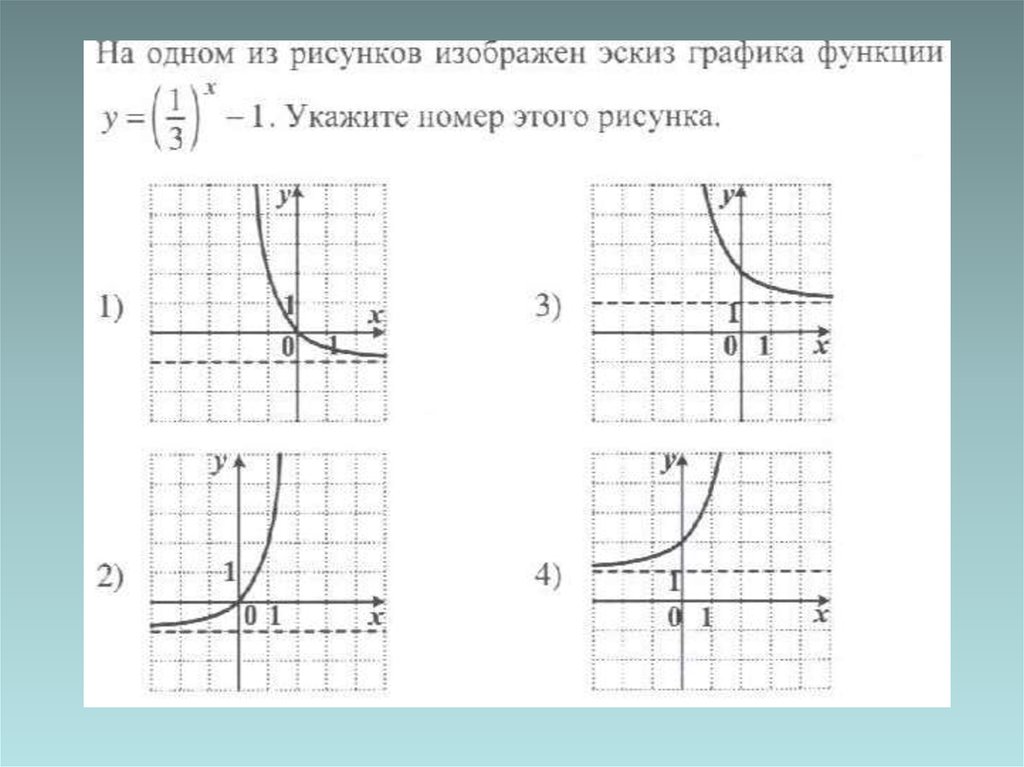
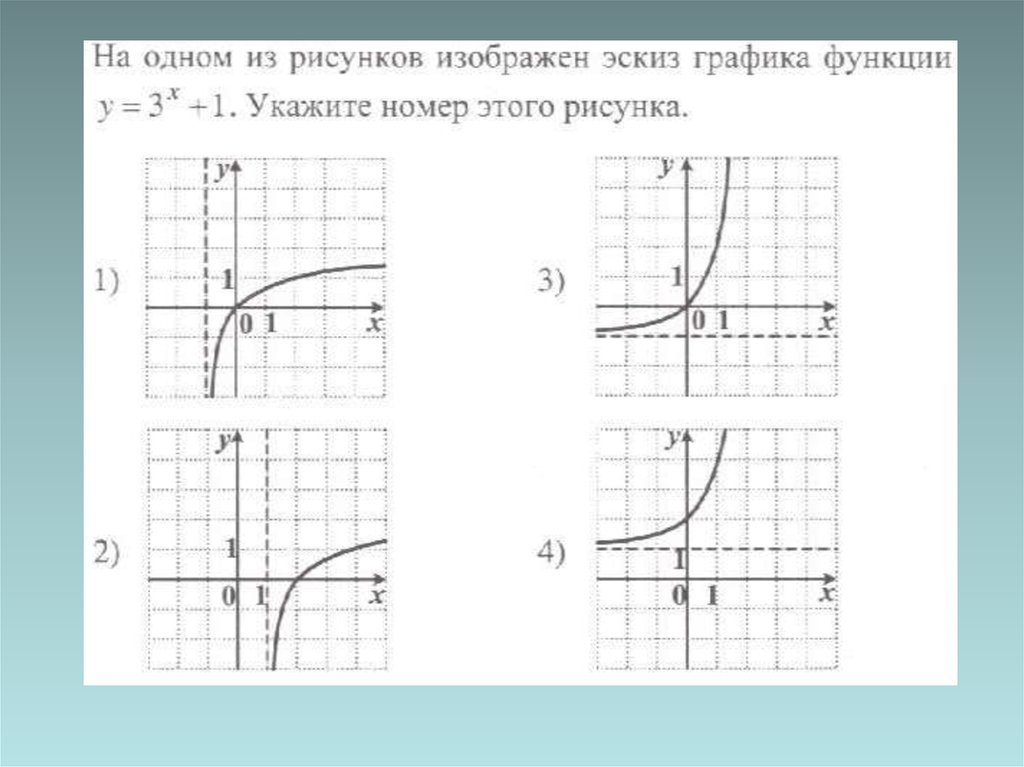
 medicine
medicine








