Similar presentations:
Свойства числовых неравенств
1. Отличного настроения!
Верныхсуждений!
Новых
впечатлений!
Отличного
настроения!
Мира!
Превосходного результата!
2.
Информацияоб объекте
• Полезная
•Полная
• Понятная
• Актуальная
•Достоверная
• Форма
Твердое
тело
Равнобедренный
треугольник
•Объем
•Цвет
•Плотность
С
В
О
Й
С
Т
В
А
• Углы при основании равны.
•Биссектриса, проведенная к основанию, является
медианой и высотой.
•Медиана, проведенная к основанию, является
биссектрисой и высотой.
•Высота, проведенная к основанию, является
биссектрисой и медианой.
3.
..
4.
НЕ
Р
А
В
Е
Н
С
Т
В
А
5.
СВ
О
Й
С
Т
В
А
Н
Е
Р
А
В
Е
Н
С
Т
В
А
6. Свойства числовых неравенств
7.
«Мы с наслаждениемпознаём математику…
Она восхищает нас, как
цветок лотоса».
Аристотель
8. Как называется запись отношений двух неравных чисел: 5>3
Как называетсязапись отношений
двух неравных чисел:
5>3
числовое неравенство.
9.
10.
Шаг1• Фото кубика!
11.
Шаг 212.
• Фото кубика!Шаг3
13.
№1• Фото кубика!
Шаг 4
14.
Радости!Надежных
Друзей!
Мудрости!
15. Работа в группе!
• Часы – «Диспетчер» (хранитель времени) – следитза временем и регламентом.
• Ручки – «Исполнитель» – выполняют конкретные
простые действия, необходимые для реализации
групповой задачи (подсчёт, решение поставленных
задач, оформление).
• Книжка – «Глашатай» – озвучивает общее решение
группы, заносит результат в общую схему.
• Очки – «Совесть группы» – напоминает об общей
идее, групповой этике, поднимает настроение.
16. Вывод свойств числовых неравенств
17. Вишня легче яблока
Вишня склубникой
легче
а
яблока с
клубникой
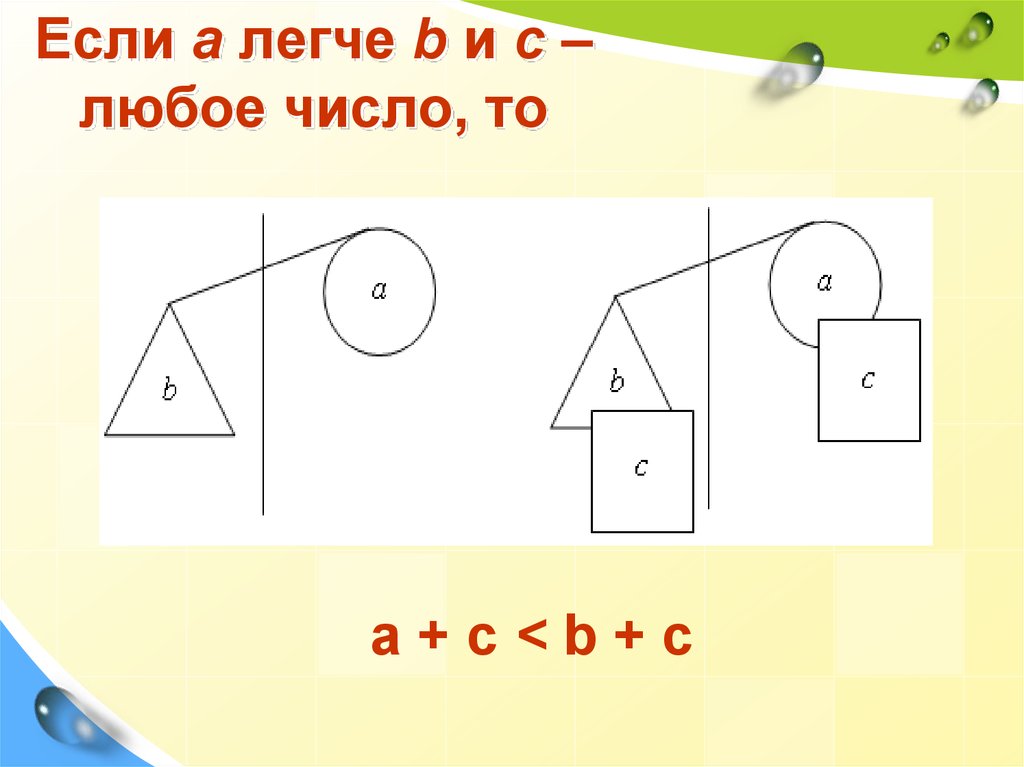
18. Если а легче b и с – любое число, то
а + с <b + c19.
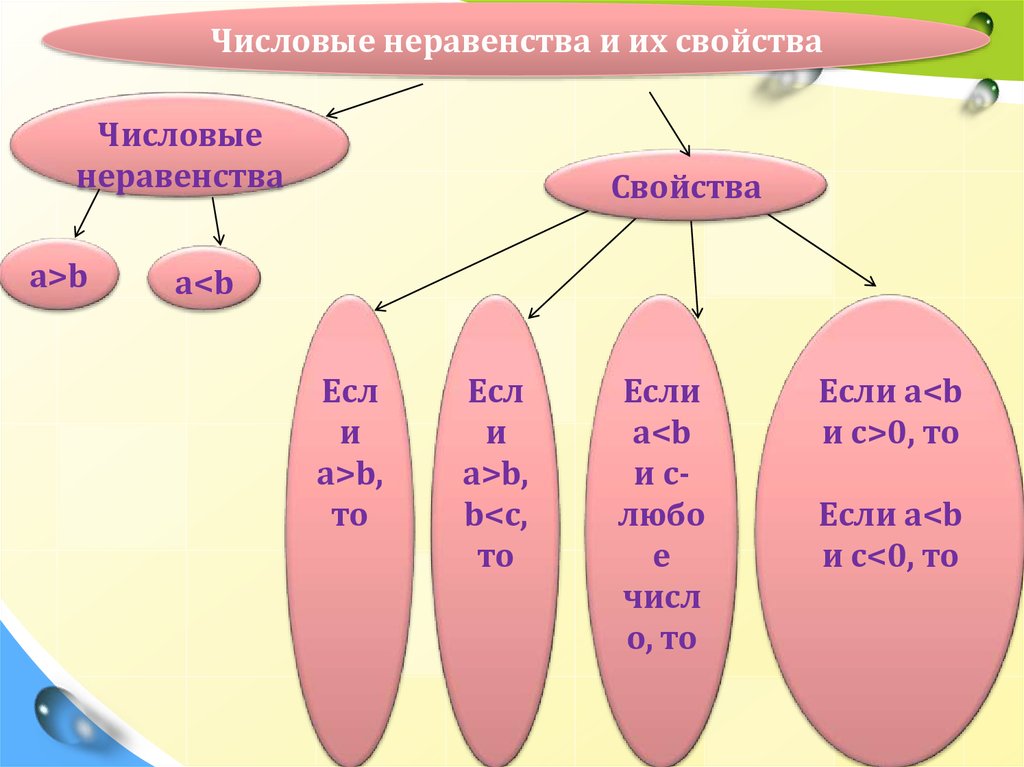
Числовые неравенства и их свойстваЧисловые
неравенства
a>b
Свойства
a<b
Есл
и
a>b,
то
Есл
и
a>b,
b<с,
то
Если
a<b
и слюбо
е
числ
о, то
Если a<b
и с>0, то
Если a<b
и с<0, то
20.
5х≤100Так как 5>0, то
5/5х≤100/5
х≤20
21. Лаборатория эрудитов
22.
23.
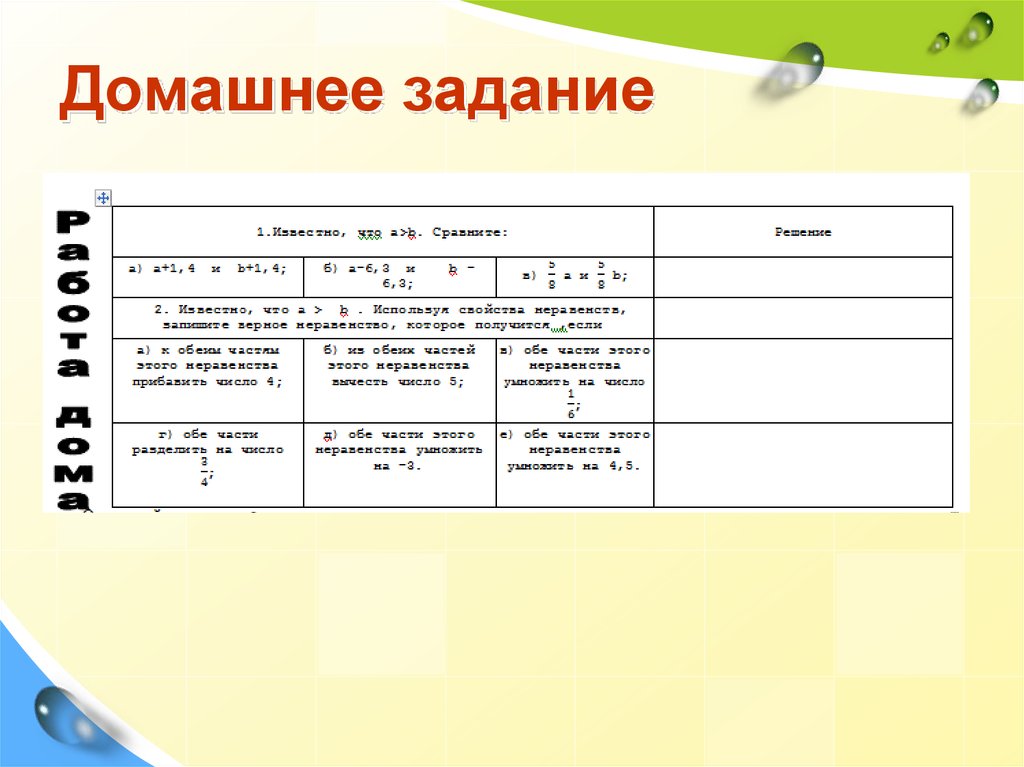
24. Домашнее задание
25. Оцени себя
26.
27. Thank You!
28.
Числовые неравенства и их свойстваЧисловые
неравенства
a>b
Свойства
a<b
Есл
и
a>b,
то
b<a
Есл
и
a>b,
b<с,
то
а<c
Если
a<b
и слюбо
е
числ
о, то
а+с<
b+с
Если a<b
и с>0, то
ас<bс
(а/с<b/с);
Если a<b
и с<0, то
ас>bс
(а/с>b/с)

















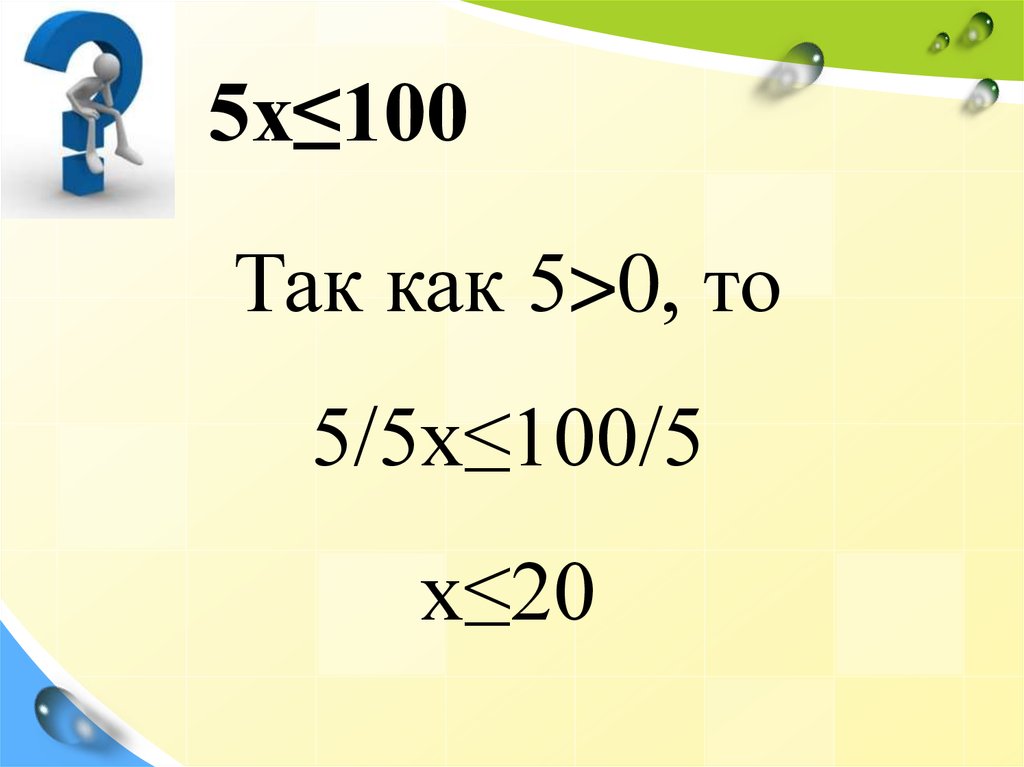







 mathematics
mathematics








