Математические модели задач на движение или работу

1. Построение математической модели задач на движение или работу

ПОСТРОЕНИЕ
МАТЕМАТИЧЕСКОЙ
МОДЕЛИ ЗАДАЧ НА
ДВИЖЕНИЕ ИЛИ РАБОТУ
Подготовила учитель
математики МКОУ
«Вилинская СОШ № 1»
Кулик И. А.

2. Заполнение таблиц (t*v=s, t*p=a)

ЗАПОЛНЕНИЕ ТАБЛИЦ
(T*V=S,
T*P=A) Производительность
Название Время
(Скорость)
Работа
(пройденный
путь)

3. Задача 5 класса (учебник С. М. Никольский № 961)

ЗАДАЧА 5 КЛАССА
(УЧЕБНИК С. М. НИКОЛЬСКИЙ № 961)
Два печника сложили печь за 16 ч.
Известно, что первый из них,
работая один, сложил бы печь за
24 ч. За сколько часов второй
печник, работая один, сложил бы
ту же печь?

4. Указание к решению задачи

УКАЗАНИЕ К РЕШЕНИЮ ЗАДАЧИ
Примите всю работу за 1.
Заполните столбец соответствующий времени работы.
Найдите производительность, какую часть печи сложат два печника за 1
час, работая вместе (разделив работу на время).
Найдите, какую часть печи сложит первый печник за 1 ч, работая один
(разделив работу на время).
Вычислите разность между найденными частями.
Ответьте на вопрос задачи.

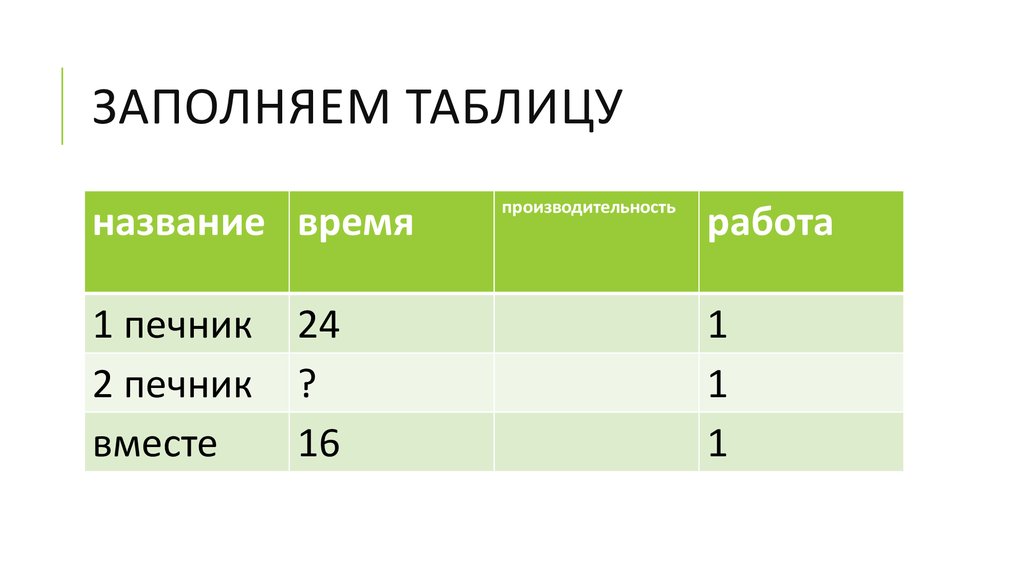
5. Заполняем таблицу

ЗАПОЛНЯЕМ ТАБЛИЦУ
название время
1 печник
2 печник
вместе
24
?
16
производительность
работа
1
1
1

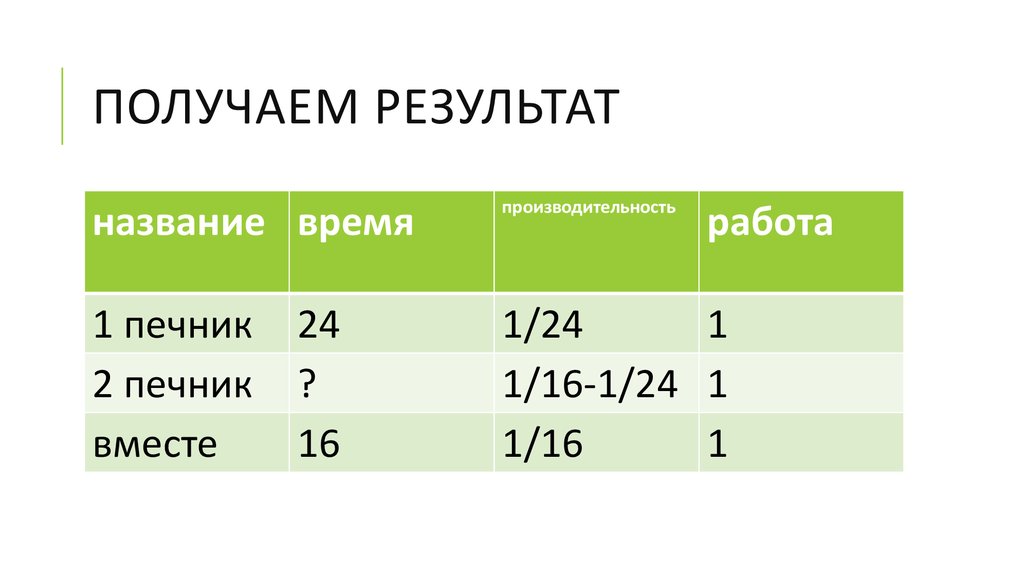
6. Получаем результат

ПОЛУЧАЕМ РЕЗУЛЬТАТ
название время
производительность
1 печник
2 печник
вместе
1/24
1
1/16-1/24 1
1/16
1
24
?
16
работа

7. Задача 6 класса ( учебник А. Г. Мерзляк № 1206)

ЗАДАЧА 6 КЛАССА
( УЧЕБНИК А. Г. МЕРЗЛЯК № 1206)
Пешеход преодолел расстояние
между двумя поселками за 7 ч, а
всадник – за 3 ч. Найдите скорости
пешехода и всадника, если скорость
пешехода на 5,6 км/ч меньше
скорости всадника.

8. Заполняем таблицу

ЗАПОЛНЯЕМ ТАБЛИЦУ
название время
пешеход 7
всадник
3
скорость расстояние
х
Х+5,6

9. Находим пройденный путь

НАХОДИМ ПРОЙДЕННЫЙ ПУТЬ
название
время
скорость расстояние
пешеход
7
х
всадник
3
Х+5,6 3(х+5,6)
7х

10. Из последнего столбца получаем уравнение

ИЗ ПОСЛЕДНЕГО СТОЛБЦА
ПОЛУЧАЕМ УРАВНЕНИЕ
1) 7х =3(х+5,6)
х=16,8:4
7х =3х+16,8
х=4,2
7х-3х = 16,8
2) 4,2+5,6=9,8
4х=16,8
Ответ: 4,2 и 9,8

11. Задача 8 класса ( учебник Ю. Н. Макарычев № 632 )

ЗАДАЧА 8 КЛАССА
( УЧЕБНИК Ю. Н. МАКАРЫЧЕВ № 632 )
При совместной работе двух кранов
разгрузку баржи закончили за 6 ч. Сколько
времени потребовалось бы каждому крану
отдельно для разгрузки баржи, если
известно, что первому крану для этого
требуется на 5ч больше, чем второму?

12. Заполняем таблицу

ЗАПОЛНЯЕМ ТАБЛИЦУ
название Время
t
1 кран
х+5
Производительность
Р
Работа
А
1
2 кран
х
1
вместе
6
1

13. Находим производительность (скорость выполнения работы за единицу времени)

НАХОДИМ ПРОИЗВОДИТЕЛЬНОСТЬ (СКОРОСТЬ
ВЫПОЛНЕНИЯ РАБОТЫ ЗА ЕДИНИЦУ ВРЕМЕНИ)
название Время
t
1 кран
х+5
Производительность
1/(х+5)
Работа
А
1
2 кран
х
1/х
1
вместе
6
1/6
1
Р

14. Составим и решим уравнение

СОСТАВИМ И РЕШИМ УРАВНЕНИЕ
1) 1/(х+5)+1/х=1/6 помножим на 6х(х+5), т. к. х≠0, х≠-5
6х+6(х+5)=х(х+5)
6х+6х+30=х²+5х
х²+5х-6х-6х-30=0
х²-7х-30=0
х=-3(не подходит по условию) или х=10(ч) – 2 кр.
2) 10+5=15(ч) – 1 кр.
Ответ: 5 ч и 10 ч.

15. Задача 9 класса (сборник И. В. Ященко Типовые экзаменационные варианты № 22, вариант 23)

ЗАДАЧА 9 КЛАССА
(СБОРНИК И. В. ЯЩЕНКО ТИПОВЫЕ ЭКЗАМЕНАЦИОННЫЕ
ВАРИАНТЫ № 22, ВАРИАНТ 23)
Из пункта А в пункт В, расположенный ниже по
течению реки, отправился плот. Одновременно
с ним из пункта А вышел катер. Дойдя до В
катер сразу же развернулся и пошел назад.
Какую часть пути от А до В проплывет плот к
моменту встречи с катером, если скорость
катера в стоячей воде втрое больше скорости
течения реки?

16. Заполняем таблицу

ЗАПОЛНЯЕМ ТАБЛИЦУ
название
Плот
Катер по
течению
Катер
против
течения
t
v
у
3у+у
3у-у
s
х
1
1-х

17. Находим время затраченное на путь

НАХОДИМ ВРЕМЯ ЗАТРАЧЕННОЕ НА ПУТЬ
название t
v
s
Плот
Катер по
течению
Катер
против
течения
х/у
у
1/4у
4у
(1-х)/2у 2у
х
1
1-х

18. Составим и решим уравнение

СОСТАВИМ И РЕШИМ УРАВНЕНИЕ
х/у=1/4у+(1-х)/2у т.к. у≠0, помножим на 4у
4х=1+2(1-х)
4х=1+2-2х
4х+2х=1+2
6х=3
х=1/2
Ответ: 1/2