Similar presentations:
Великолепный часослов герцога Беррийского. Математика в каждом
1.
К2
полк
Как
Как вы
вы видите
видите это
это слово?
слово?
Кто-то
Кто-то видит
видит это
это слово
слово так,
так, кто-то
кто-то так,
так, лично
лично я
я вижу
вижу это
это слово
слово так
так «К/2»
«К/2»
Каждый
Каждый человек
человек воспринимает
воспринимает любое
любое слово
слово или
или понятие
понятие по-разному,
по-разному, и
и здесь
здесь нет
нет правых
правых и
и
неправых.
неправых.
Вопрос
Вопрос лишь
лишь в
в том,
том, как
как нам
нам в
в этих
этих условиях
условиях верно
верно понимать
понимать друг
друг друга.
друга.
Может
быть
всех
нас
спасет
язык
литературы?
Может быть всех нас спасет язык литературы?
а
2.
стройногороста,
Премудрой — как всякая божия
тварь.
(Марина Цветаева)
Я
Я счастлива
счастлива жить
жить образцово
образцово и
и просто
просто —Как
—Как солнце,
солнце,
как
как маятник,
маятник, как
как календарь.Быть
календарь.Быть светской
светской
пустынницей
пустынницей стройного
стройного роста,Премудрой
роста,Премудрой —
— как
как
всякая
всякая божия
божия тварь.
тварь.
Писала
Писала Марина
Марина Цветаева
Цветаева
Было
Было бы
бы великолепно,
великолепно, если
если все
все общались
общались языком
языком
поэзии...
поэзии...
Может
Может быть
быть нам
нам поможет
поможет такая
такая перспективная
перспективная
ныне
ныне наука
наука как
как химия?
химия?
3.
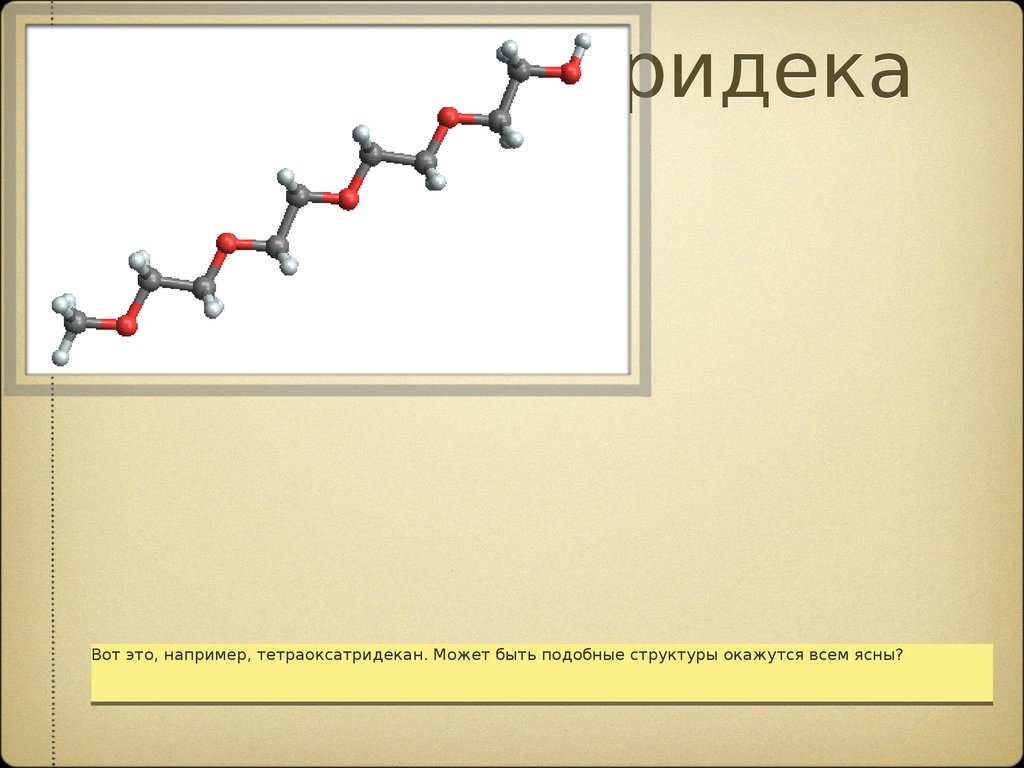
Тетраоксатридекан
Вот
Вот это,
это, например,
например, тетраоксатридекан.
тетраоксатридекан. Может
Может быть
быть подобные
подобные структуры
структуры окажутся
окажутся всем
всем ясны?
ясны?
4.
ИлиИли может
может быть
быть иностранные
иностранные языки?
языки?
Например,
Например, японский?
японский?
5.
«Великолепныйчасослов
герцога Беррийского»
Февраль
Май
Очень
Очень красивый
красивый язык
язык искусство.
искусство. Вот
Вот эти,
эти,
допустим,
допустим, изображения
изображения последних
последних месяцев
месяцев
сезона
Братьев
Лимбург
в
«Великолепном
сезона Братьев Лимбург в «Великолепном
часослове
часослове герцога
герцога Беррийского»?
Беррийского»?
Август
Ноябрь
Братья
Лимбург
6.
Я счастлива жить образцово ипросто —
Как солнце, как маятник, как
календарь.
Тетраоксатридека
Но
Но есть
есть язык,
язык, с
с точки
точки зрения
зрения которого
которого это
это стихотворение,
стихотворение, это
это
вещество,
вещество, эти
эти японские
японские буквы
буквы и
и месяцы
месяцы -- одно
одно и
и то
то же
же
Февраль Май Август Ноябрь
7.
образцОво и прОсто—
Как сОлнце, как
мАятник,
кАк календАрь.
Давайте
Давайте посмотрим
посмотрим на
на них
них повнимательнее:
повнимательнее:
просто
просто подчеркнем
подчеркнем слоги,
слоги, и
и выделим
выделим ударные
ударные в
в первых
первых двух
двух строках:
строках:
и
и запишем
запишем схему,
схему, так
так обычно
обычно поступают,
поступают, когда
когда выясняют
выясняют каким
каким слогом
слогом написано
написано
стихотворение.
это
написано
амфибрахием
трехсложной
стопой
с
ударением
стихотворение. это написано амфибрахием - трехсложной стопой с ударением на
на втором
втором
слоге.
слоге.
Сейчас
Сейчас мы
мы попросим
попросим коллег
коллег пристально
пристально рассмотреть
рассмотреть японские
японские буквы,
буквы, а
а сами
сами рассмотрим
рассмотрим
остальные
остальные примеры
примеры
-/--/--/--/--/--/--/--/
8.
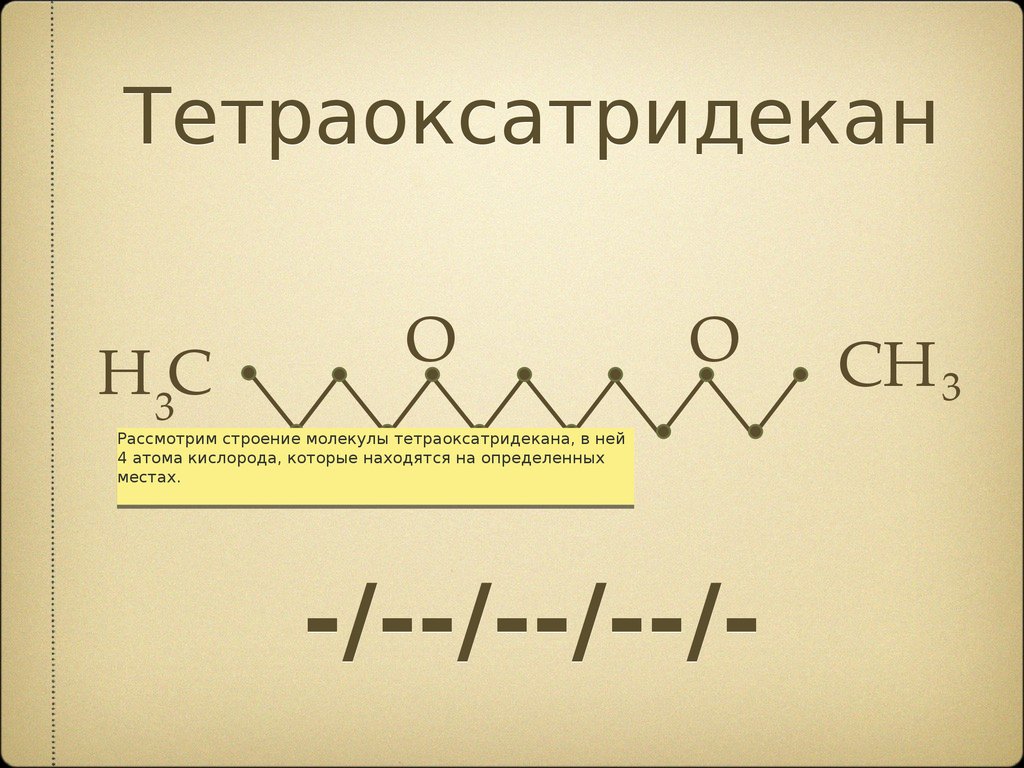
ТетраоксатридеканO
Н 3С
O
Рассмотрим
Рассмотрим строение
строение молекулы
молекулы тетраоксатридекана,
тетраоксатридекана, в
в ней
ней
4
атома
кислорода,
которые
находятся
на
определенных
4 атома кислорода, которые находятся на определенных
местах.
местах.
O
O
-/--/--/--/-
CH 3
9.
ьНоябрь
Декабр
ь
вральМартАпрельМайИюнь
-/--/--/--/-
И
И про
про месяцы
месяцы все
все становится
становится сразу
сразу понятно,
понятно, как
как только
только мы
мы выпишем
выпишем все
все месяцы
месяцы подряд.
подряд.
Те,
Те, что
что были
были в
в списке
списке выделим
выделим особенным
особенным образом
образом и
и построим
построим схему:
схему:
10.
あい
うえ
お
はひ
ふ
へほ
か
きくけこまみむめもさすせそや
ゆよたちつてとらりるれろなに
ぬねのわゐんゑを
-/--/--/--/-
наши
наши группы
группы справились
справились со
со своей
своей задачей
задачей и
и получили
получили точно
точно такую
такую же
же схему
схему
11.
-/--/--/--/-2 5 8 11
схема
схема состоит
состоит из
из палочек
палочек и
и черточек,
черточек, на
на первом
первом месте
месте находится
находится черточка,
черточка, на
на втором
втором палочка,
палочка,
выпишем
выпишем только
только те
те места,
места, где
где палочки,
палочки, получим
получим последовательность
последовательность чисел
чисел
12.
n.
a=a+3(n-1)
1
n
a=a+d(n-1)
1
.
Посмотрите,
Посмотрите, что
что мы
мы получили!
получили!
Наверняка
Наверняка в
в жизни
жизни встречаются
встречаются и
и другие
другие последовательности,
последовательности, в
в которых
которых разница
разница между
между последующим
последующим и
и
предыдущим
предыдущим членами
членами не
не 3,
3, а,
а, например,
например, 4,
4, 5
5 или
или 100!
100!
Что
бы
в
этой
нашей
записи
изменилось?
Что бы в этой нашей записи изменилось?
Тогда
Тогда давайте
давайте заменим
заменим число
число 3
3 на
на какую-нибудь
какую-нибудь переменную,
переменную, например,
например, d.
d.
Только
Только что
что мы
мы с
с вами
вами вывели
вывели формулу
формулу n-ого
n-ого члена
члена арифметической
арифметической последовательности.
последовательности.
Как?
Как?
Мы
Мы взяли
взяли примеры
примеры из
из литературы,
литературы, из
из науки,
науки, из
из искусства,
искусства, нашли
нашли в
в них
них общее,
общее, придумали,
придумали, как
как это
это
записать,
и
получили
одну
единственную
модель,
которая
описывает
все
эти
примеры!
записать, и получили одну единственную модель, которая описывает все эти примеры!
В
В этом
этом одновременно
одновременно и
и суть,
суть, и
и прелесть
прелесть математики!
математики! А
А самое
самое главное,
главное, это
это может
может сделать
сделать каждый!
каждый!
Поэтому
Поэтому сегодня
сегодня я
яи
и хочу
хочу с
с вами
вами выяснить,
выяснить, математика
математика -- это
это так
так далеко
далеко и
и непонятно
непонятно или
или все
все же
же нечто,
нечто,
окружающее
окружающее нас
нас повсеместно.
повсеместно.
13.
Математика вкаждом
или красота арифметической прогрессии
14.
Сколько очков наневидимых гранях?
15.
Сумма n первых членоварифметической
прогрессиии
S=
n
a+a
1
2
n
.n
16.
Последовательностивезде
QuickTime™ Ë a
‰ÂÍÓÏÔ ÂÒÒÓ
Ú Â·ÛÂÚÒ , ˜ÚÓ·˚ ‚ˉÂÚ¸ ˝ÚÛ Í‡ ÚËÌÍÛ.
17.
Математика — этоязык, на котором
написана книга
природы.
Галилео Галилей












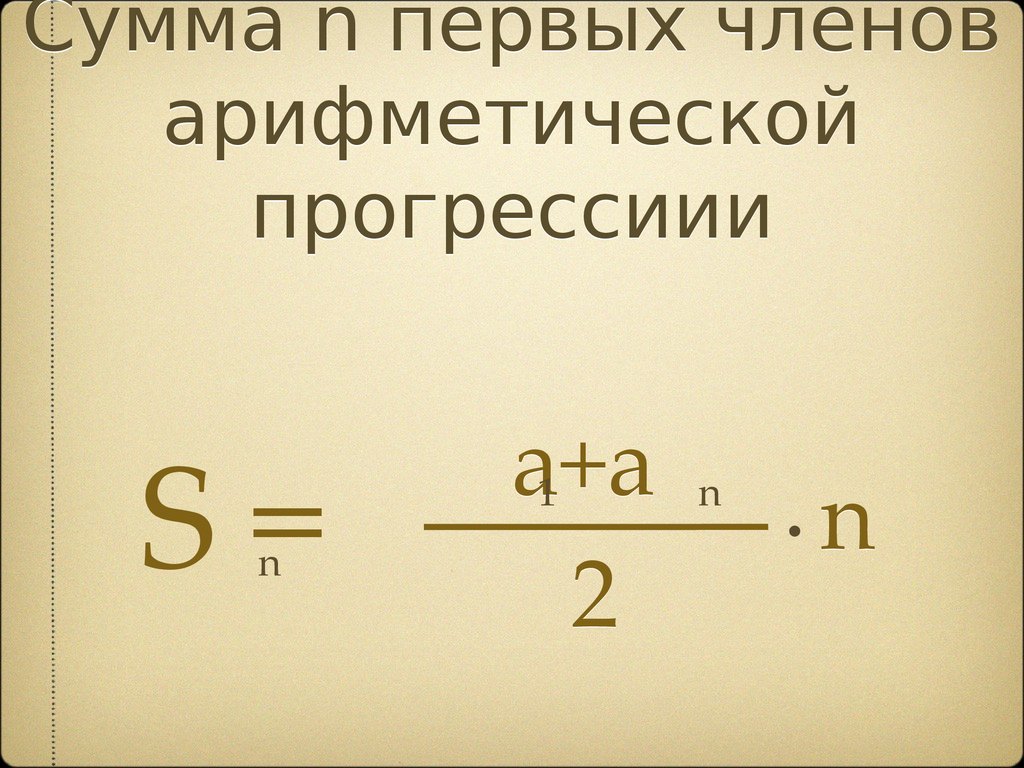


 mathematics
mathematics








