Similar presentations:
Теорема Виета. Алгебра 8 класс
1.
Теорема ВиетаАлгебра 8 класс
2.
х2 – х – 30 = 07х2 + 8х + 1= 0
2х2 – 50 = 0
2
х – 8х = 0
100х2 +97х – 197 = 0
13х2 – 18х +5 = 0
х2 – 15х +14 = 0
3.
х2 – х – 30 = 0(-5; 6)
И
7х2 + 8х + 1= 0
(-1; -1/7) В
2х2 – 50 = 0
(5; -5)
Е
х2 – 8х = 0
(0; 8)
Т
100х2 +97х – 197 = 0
13х2 – 18х +5 = 0
х2 – 15х +14 = 0
2
1
3
4
В
И
Е
Т
4.
Французский ученыйФрансуа Виет
(1540-1603)
Знаменитая теорема, устанавливающая
связь коэффициентов многочлена с его
корнями, была обнародована в 1591 г.
Теперь она носит имя Виета
5.
Задача: записать приведенное квадратноеуравнение, корнями которого были бы
числа -3; 1.
2. Не решая квадратные уравнения
определить корни?
1. х²-9х+20=0
2. х²+11х-12=0
3. х²+х-56=0
4. 13х²-18х+5=0
6.
Цели урока:Выяснить зависимость между корнями и
коэффициентами приведенного
квадратного уравнения;
Научиться применять эту зависимость
для решения задач.
7. Теорема Виета
8.
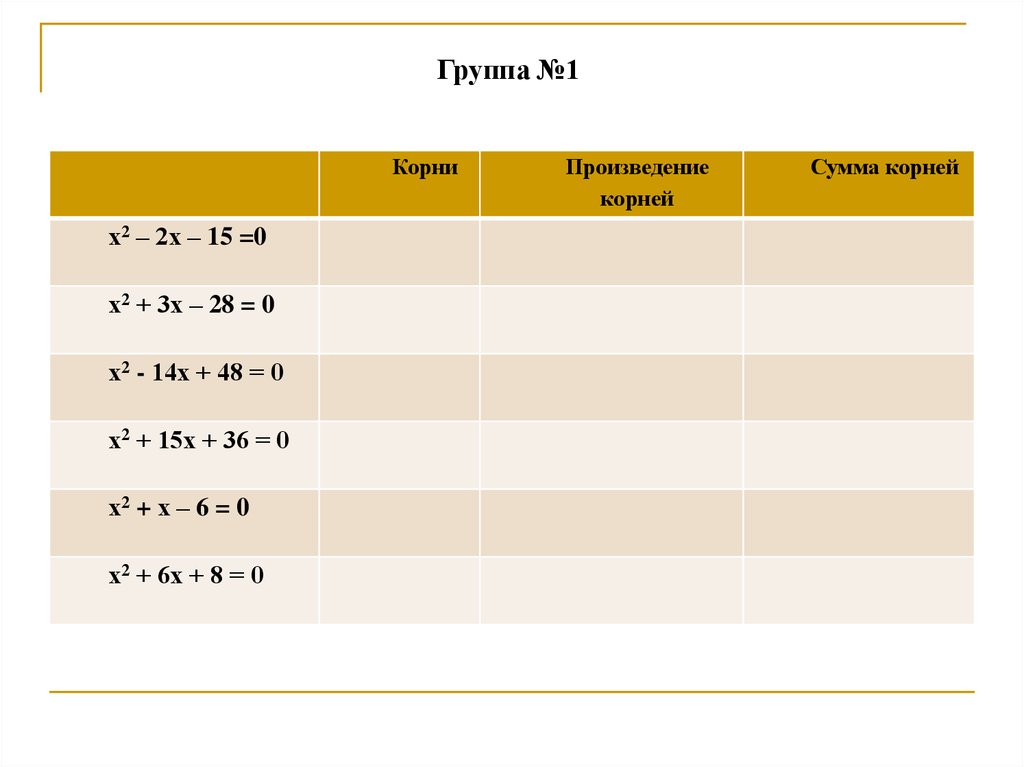
Группа №1Корни
х2 – 2х – 15 =0
х2 + 3х – 28 = 0
х2 - 14х + 48 = 0
х2 + 15х + 36 = 0
х2 + х – 6 = 0
х2 + 6х + 8 = 0
Произведение
корней
Сумма корней
9.
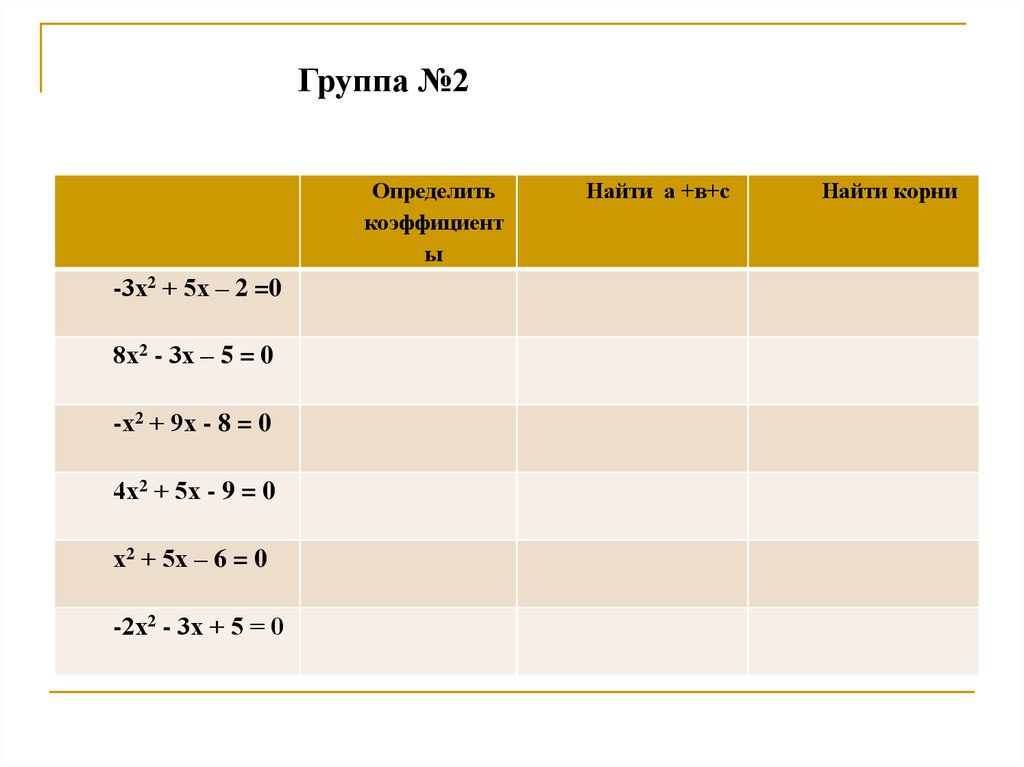
Группа №2Определить
коэффициент
ы
-3х2 + 5х – 2 =0
8х2 - 3х – 5 = 0
-х2 + 9х - 8 = 0
4х2 + 5х - 9 = 0
х2 + 5х – 6 = 0
-2х2 - 3х + 5 = 0
Найти а +в+с
Найти корни
10.
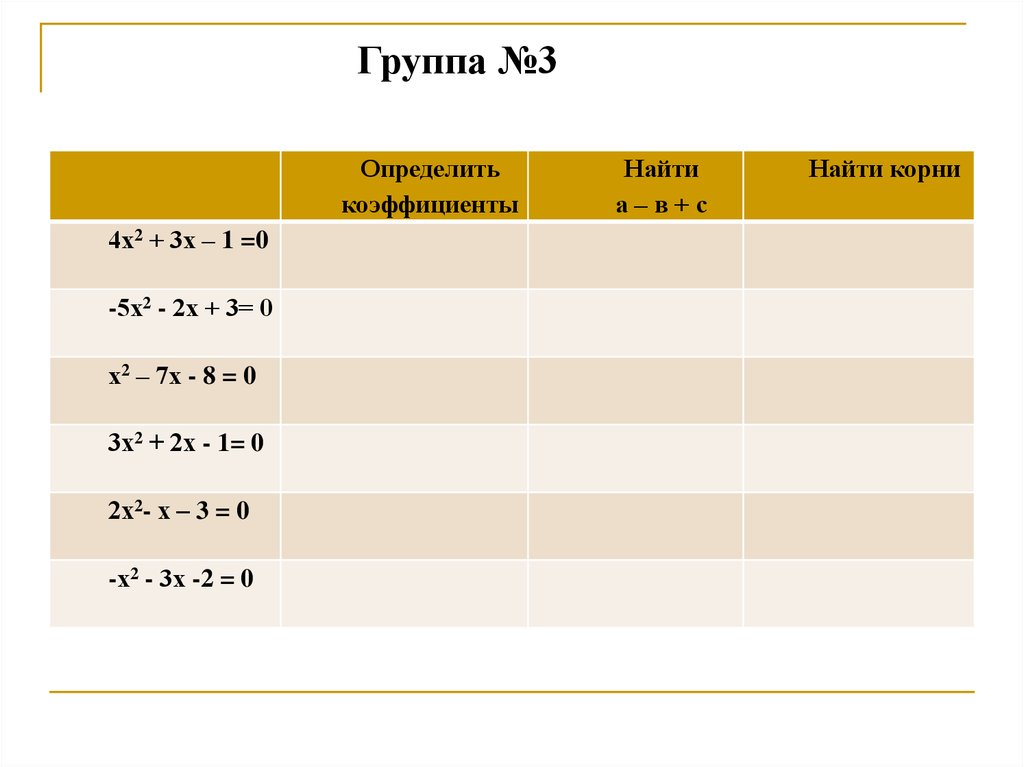
Группа №3Определить
коэффициенты
4х2 + 3х – 1 =0
-5х2 - 2х + 3= 0
х2 – 7х - 8 = 0
3х2 + 2х - 1= 0
2х2- х – 3 = 0
-х2 - 3х -2 = 0
Найти
а–в+с
Найти корни
11. Ситуации, в которых может использоваться теорема Виета: 1.Проверка правильности найденных корней. 2. Составление квадратных
уравнений сзаданными корнями.
3. Устное нахождение целых корней
приведенного квадратного уравнения.
12.
«В математике, как ни в какой другойобласти, не принимают ничего на
веру, здесь всегда требуются
доказательства»
У. Сойер

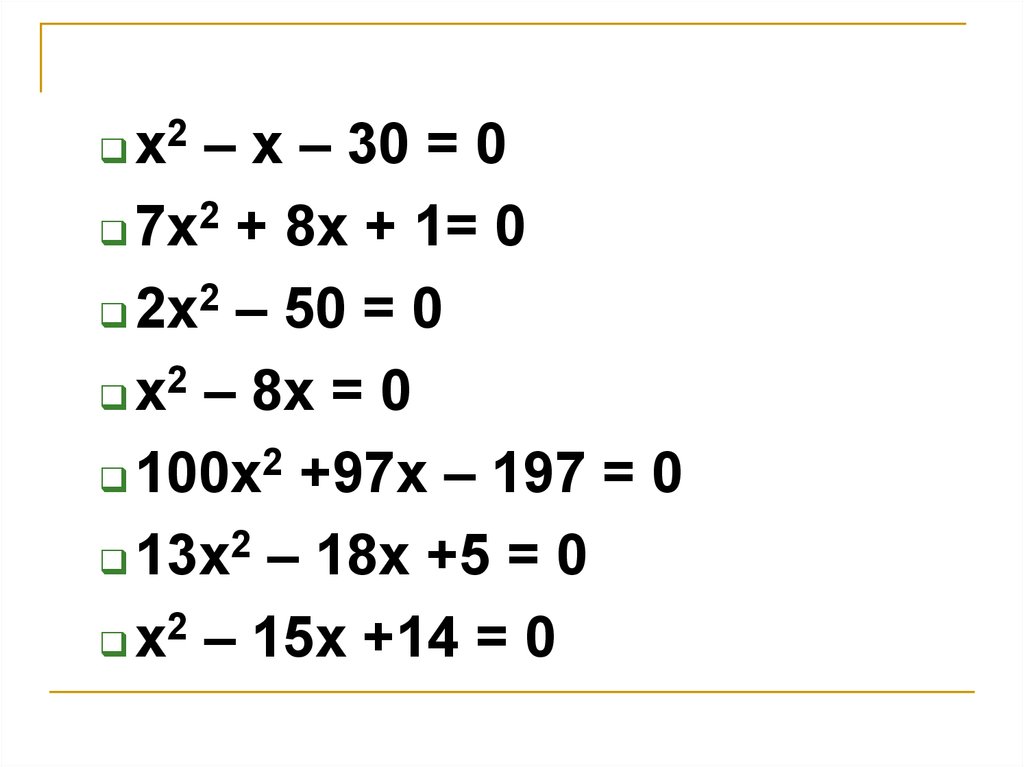







 mathematics
mathematics








