Similar presentations:
Геометрический смысл производной
1.
Тема урока:Геометрический
смысл
производной.
2.
k = f '(x₀)=tgугловой
коэффициент
касательной
значение
производной
в точке Х₀
тангенс угла
наклона
касательной к
положительном
у направлению
оси ОХ
3.
1. На рисунке изображен графикфункции y=f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение
производной в точке x0.
Подумай!
1 -0,6
y
Подумай!
2 0,8
3 1,25
y=f(x)
4 -0,8
1
0 1
x0
Подумай!
Верно!
x
Проверка
4.
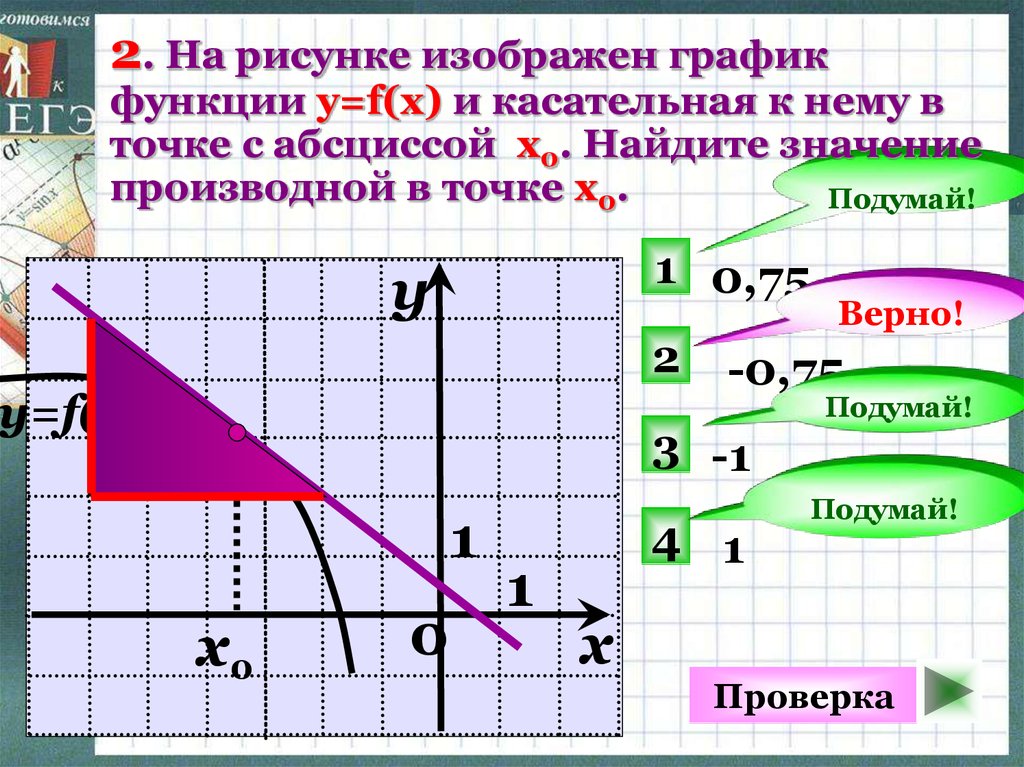
2. На рисунке изображен графикфункции y=f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение
производной в точке x0.
Подумай!
1 0,75
y
2
y=f(x)
-0,75
3 -1
1
x0
0
1
Верно!
4 1
Подумай!
Подумай!
x
Проверка
5.
3. На рисунке изображен графикфункции y=f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение
производной в точке 3.
Верно!
1 2
y
2 1
1
3 0,5
01
3
x 4 –2
Подумай!
Подумай!
Подумай!
Проверка
6.
4. На рисунке изображен графикфункции y=f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение
производной в точке x0.
1 2
y
Подумай!
Подумай!
2
1
1
3 3
01
x0
x 4 0
Подумай!
Верно!
Проверка
7.
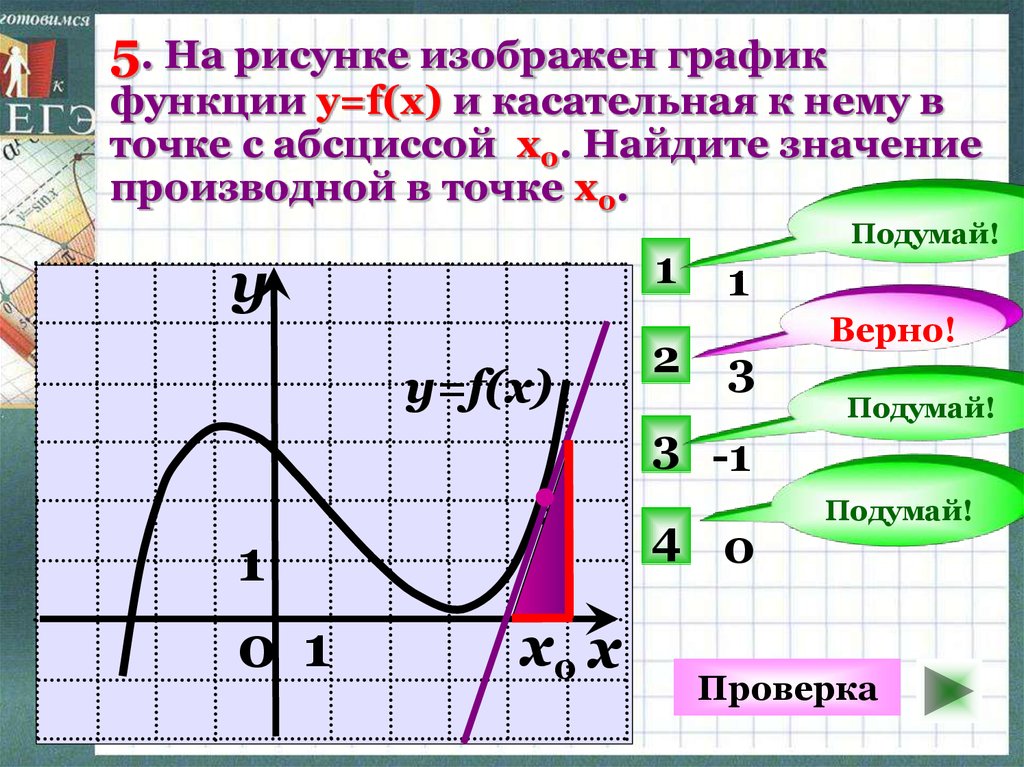
5. На рисунке изображен графикфункции y=f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение
производной в точке x0.
1
y
y=f(x)
2
Подумай!
1
3
3 -1
4 0
1
0 1
x0 x
Верно!
Подумай!
Подумай!
Проверка
8.
6. На рисунке изображен графикфункции y=f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение
производной в точке x0.
y
1 2
x0
x
1
y=f(x)
Подумай!
Верно!
3 0,5
4 -1,5
1
0 1
2
Подумай!
Подумай!
Проверка
9.
Тема урока:06.07.2019
Геометрический
смысл
производной.
Учитель математики МБОУ СОШ № 25 г. Крымска Е.В. Малая
10.
7. Найдите абсциссу точки x0 , в которойкасательная к графику функции
наклонена под углом 1350 .
ОДЗ: 5 2x 0
y 5 2x
Решение.
f ´(x₀)=tgα=k tg135 1
1
1
y
(5 2 x)
2 5 2x
5 2x
0
Получаем уравнение:
1 5 2 x ; 1 5 2 x;
x=2 входит ОДЗ
=
x 2
x0 = 2
11.
8. Функция y=f(x) определена на (–1;7).Используя изображенный на рисунке
график производной y=f ′(x) , определите
количество касательных к графику
функции, которые составляют угол 600 с
положительны направлением оси Ox.
y
Решение.
tg α = tg 600 =
y=f '(x)
3 = f '(x)
3< 2
1<
=
3
1
0 1
3 точки
x
В8 3
12.
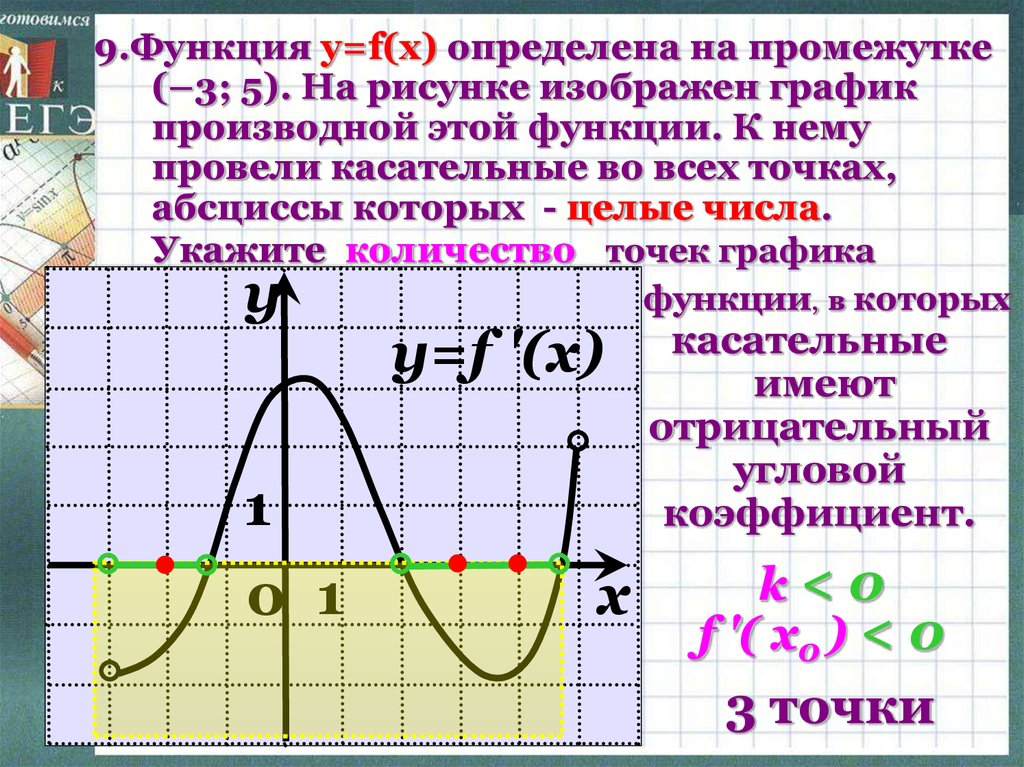
9.Функция y=f(x) определена на промежутке(–3; 5). На рисунке изображен график
производной этой функции. К нему
провели касательные во всех точках,
абсциссы которых - целые числа.
Укажите количество точек графика
y
функции, в которых
y=f '(x)
1
0 1
x
касательные
имеют
отрицательный
угловой
коэффициент.
k<0
f '( x0 ) < 0
3 точки
13.
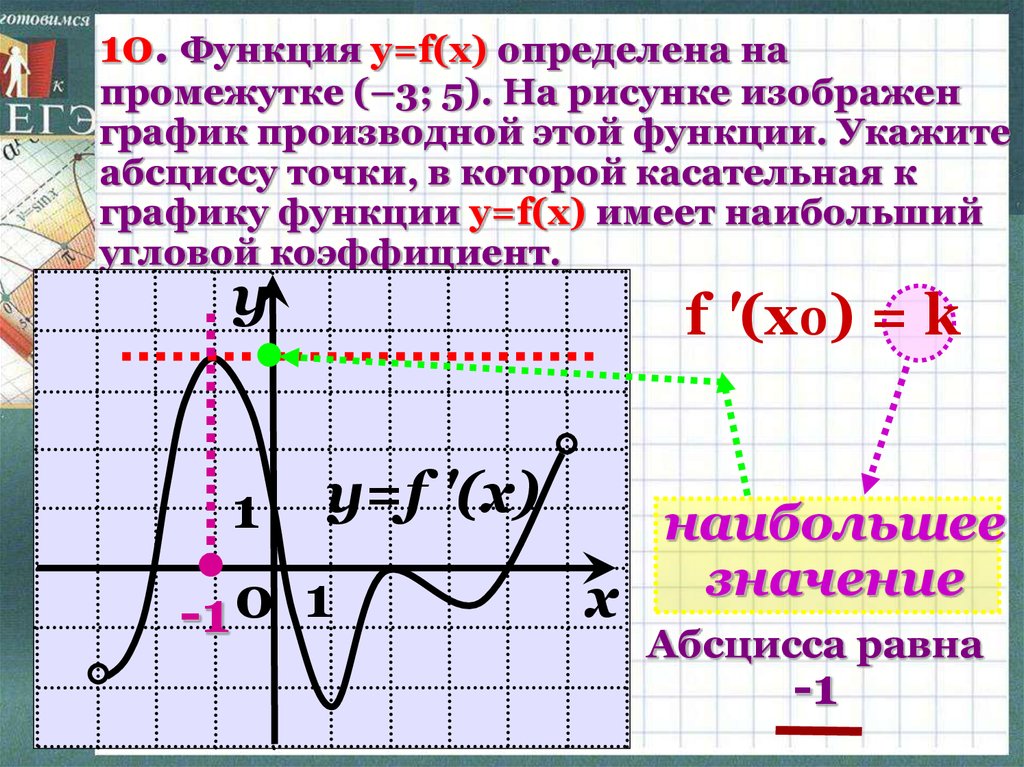
10. Функция y=f(x) определена напромежутке (–3; 5). На рисунке изображен
график производной этой функции. Укажите
абсциссу точки, в которой касательная к
графику функции y=f(x) имеет наибольший
угловой коэффициент.
y
1
f '(x₀) = k
y=f '(x)
-1 0 1
наибольшее
значение
x
Абсцисса равна
-1









 mathematics
mathematics








