Similar presentations:
Квадратичная функция в задачах с параметрами
1. Квадратичная функция в задачах с параметрами
По материалам заданий ЕГЭ и ГИА2.
Квадратичная функцияв задачах с параметрами
• Наибольшее и наименьшее значение,
принимаемое квадратичной функцией.
• Расположение корней квадратного трехчлена
относительно заданных точек.
• График квадратичной функции.
3.
• При каких значениях параметра а функцияy
2 ax 7
2
x2
имеет максимум в точке х=4.
4.
y2
ax 7
2
x
2
2
х 2 ах 7
2 монотонно возрастает,
t
f ( x) x ax 7
2
а а
хв ,
4,
2 2
а 8.
5.
• Найти все значения параметра а, при каждомиз которых наименьшее значение функции
f ( x) 2ax x 8 x 7
2
больше 1.
6. Найти все значения параметра а, при каждом из которых наименьшее значение функции больше 1.
Найти все значения параметра а, при каждом из которых наименьшее значениефункции f ( x) 2ax x 2 8 x 7 больше 1.
х 7,
х 1
f ( x) x 2 (2a 8) x 7
1 x 7
f ( x) x ( 2a 8) x 7
2
x0 4 a
x0 4 a
7. Найти все значения параметра а, при каждом из которых наименьшее значение функции больше 1.
Найти все значения параметра а, при каждом из которых наименьшее значениефункции f ( x) 2ax x 2 8 x 7 больше 1.
Функция может принимать наименьшее значение
только в ттх 1, или х 7, или х 4 - а, если 4 - а 1;7
8. Найти все значения параметра а, при каждом из которых наименьшее значение функции больше 1.
Найти все значения параметра а, при каждом из которых наименьшее значениефункции f ( x) 2ax x 2 8 x 7 больше 1.
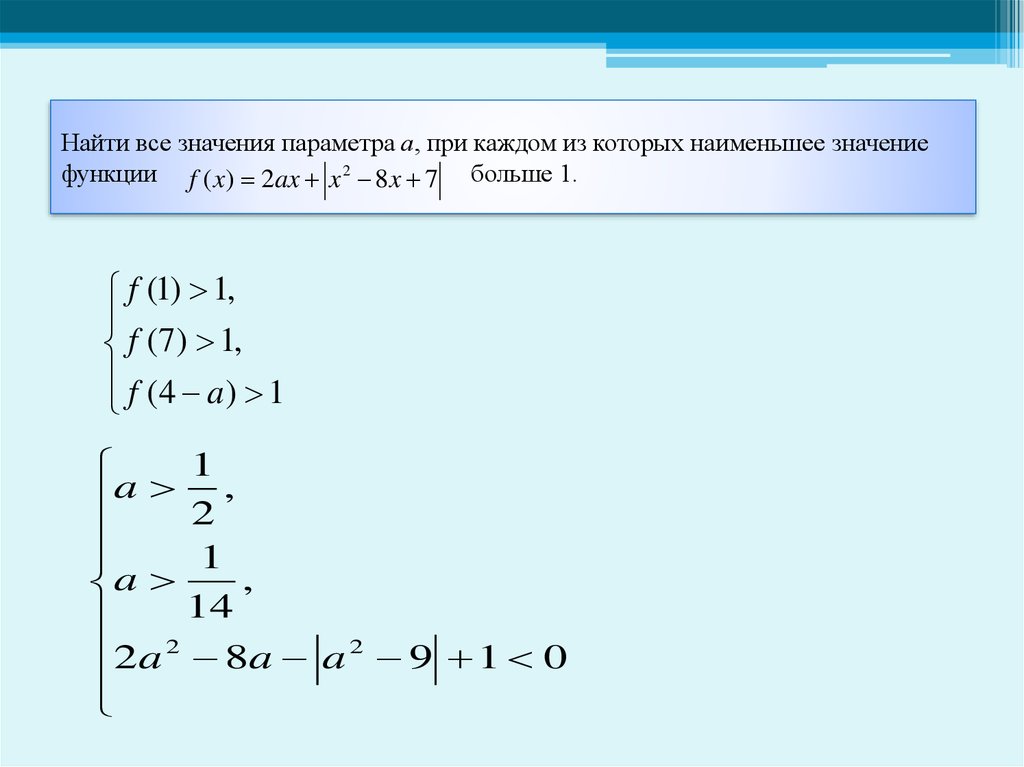
f (1) 1,
f (7) 1,
f (4 a) 1
1
a 2 ,
1
,
a
14
2a 2 8a a 2 9 1 0
9. Найти все значения параметра а, при каждом из которых наименьшее значение функции больше 1.
Найти все значения параметра а, при каждом из которых наименьшее значениефункции f ( x) 2ax x 2 8 x 7 больше 1.
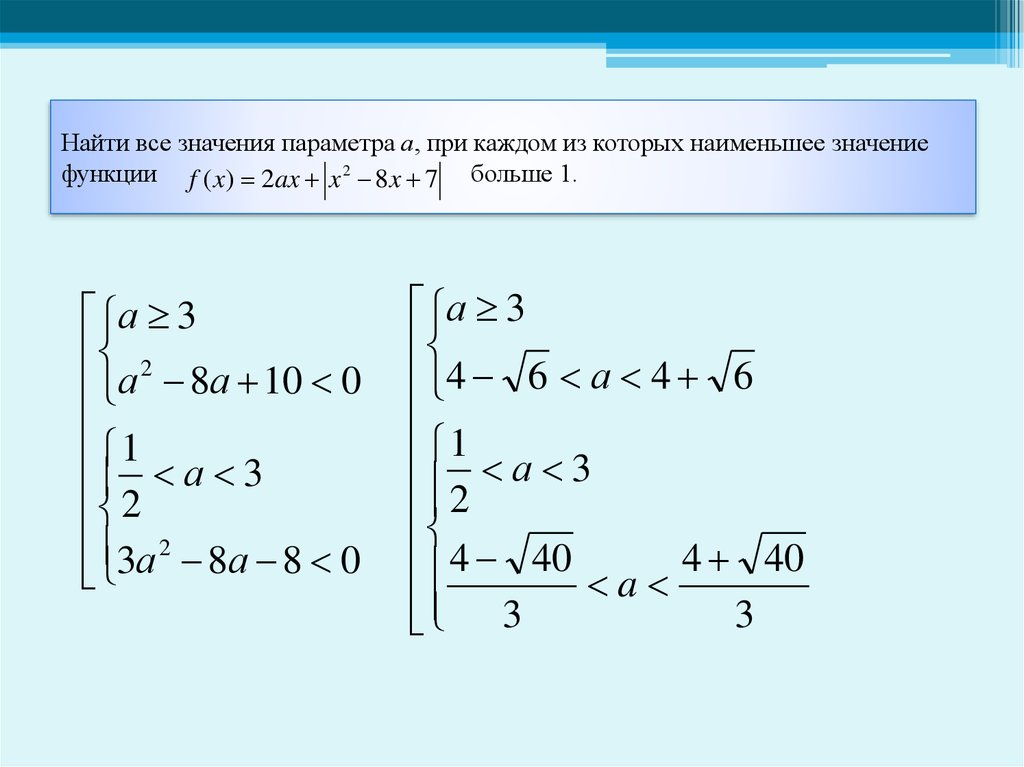
а 3
2
а 8а 10 0
1
а 3
2
3а 2 8а 8 0
а 3
4 6 а 4 6
1 а 3
2
4 40 a 4 40
3
3
10.
3 а 4 6 ,1 a 3
2
1
Ответ : а ;4 6 .
2
11.
Найти все значения параметра а, при каждомиз которых функция
f ( x) x 2 2 х а 2 8 х
имеет более двух точек экстремума
12. Найти все значения параметра а, при каждом из которых функция имеет более двух точек экстремума
Найти все значения параметра а, при каждом из2
2
которых функция f ( x) x 2 х а 8 х
имеет более двух точек экстремума
f ( x) x 2 10 x 2а 2
х а 2
f ( x) x 2 6 x 2а 2
х а 2
13.
Функция имеет более двух точек экстремуматогда и только тогда , когда точка х а 2
является ее точкой максимума,
т.е. 3 а 2 5
Ответ: а 5; 3 ( 3; 5 ).











 mathematics
mathematics








