Сравнительный анализ софизмов и парадоксов

1. Сравнительный анализ софизмов и парадоксов

Выполнила: Светловская
Дарья,
ученица 9 кл.
Руководитель: Кузьмина
Наталья Игоревна

2.

Цели и задачи
Цель:
доказать, что поиск заключенных в софизмах
ошибок, ясное понимание их причин ведут к
осмысленному постижению математики.
Задачи:
познакомиться с понятиями «софизм»,
«парадокс».
провести сравнительного анализа понятий
«софизм» и «парадокс»
познакомиться с историей возникновения
софизмов и парадоксов
познакомиться с классификацией софизмов и
ошибок в них

3.

Экскурс в историю
Первые софизмы появились в Древней Греции.
Софистика - сознательное применение в
споре или в доказательствах неправильных
доводов, софизмов, то есть всякого рода
уловок, замаскированных внешней,
формальной правильностью
Ошибкам в геометрических доказательствах
Евклид посвятил целую книгу
Появление софизмов заставило задуматься
математиков о логическом строении геометрии и
арифметики.

4.

Софизм
-ложное
умозаключение,
которое при
поверхностном
рассмотрении
кажется
правильным.
« То, что ты не потерял,
ты имеешь; ты не потерял
рога, следовательно, ты их
имеешь".
В. И. Обреимова «Математические
софизмы»

5. Парадокс

- высказывание,
противоречащее
(иногда только на
первый взгляд)
здравому смыслу.
Парадокс лжеца: «То,
что я утверждаю сейчас,
ложно»
Сначала парадоксы
рассматривались только
как продукт философских
измышлений, теперь
наука признала их
полноправными членами
сообщества научных
проблем .

6. Сравнительный анализ понятий

Софизмы, как и парадоксы, намеренно
противоречат здравому смыслу
Софизмы и парадоксы одинаково остроумны и
ироничны
Целью парадокса
Целью софизма
является доказать
является выдать
заведомую ложь
ложь за истину
истинными аргументами
Огромное число математических софизмов
строится на основе парадоксов

7.

«Парадокс - это истина,
обряженная ложью. А софизм –
это ложь, обряженная в истину.»
Даниил Гранин

8.

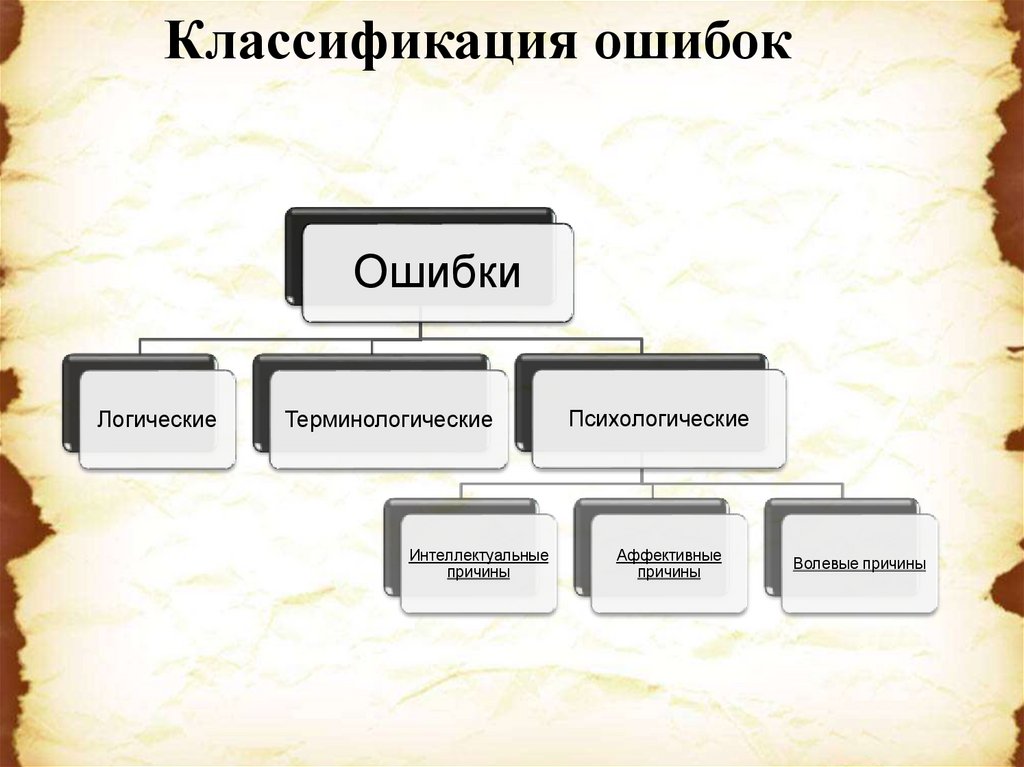
Классификация ошибок
Ошибки
Логические
Терминологические
Интеллектуальные
причины
Психологические
Аффективные
причины
Волевые причины

9. Терминологические ошибки

Грамматические, терминологические и
риторические источники софизмов выражаются в
неточном или неправильном словоупотреблении и
построении фразы .
«все углы треугольника равны π»
«сумма углов треугольника равна π»

10. Психологические ошибки

Во всяком обмене мыслей предполагается
взаимодействие между 2 лицами.
Правдоподобность софизма зависит от ловкости
того, кто защищает его, и уступчивости
оппонента.
«Лекарство, принимаемое больным, есть добро. Чем
больше делать добра, тем лучше. Значит, лекарств
нужно принимать как можно больше».

11. Тезис "не вытекает" из доводов

Тезис "не вытекает" из доводов
«Доказательство» теоремы о сумме
внутренних углов треугольника, не
опирающееся на аксиому параллельных
прямых.
Имеем:
1. A 1 3
2.
x 180
x
C 2 4 x
Сложив:
( A C 1 2) ( 3 4) 2 x
В итоге: х + 180о=2х и х=180о

12. Подмена понятий

•«Все металлы — простые тела,
бронза — металл: бронза — простое
тело»
•«Все люди смертны, святые – люди,
значит, святые смертны"

13.

«Дамский» аргумент
Суть этого
софизма в том, что
по многим вопросам
возможно, мыслимо
не одно, не два, а
несколько решений.
Некоторые из них
противоположны
друг другу.
Навязанное следствие
Софист,
доказывая свое
утверждение,
старается
навязать мысли
нелепое следствие,
которое вовсе из нее
не вытекает.

14. Многовопросие

- Знаешь ли ты, о чем я хочу тебя спросить?
- Нет.
- Знаешь ли ты, что добродетель есть добро?
- Знаю.
- Вот об этом я и хотел тебя спросить.

15.

Круг в доказательстве
«Новое доказательство» теоремы
Пифагора
Возьмём прямоугольный треугольник
с катетами a и b, гипотенузой c и
острым углом , противолежащим
катету a.
Имеем: a = c sin , b = c cos , откуда a
а2 = c2 sin2 ,
b2 = c2 cos2 .
Просуммировав по частям эти
равенства, получаем:
a2 + b2 = c2 (sin2 + cos2 ).
Но sin2 + cos2 = 1, и поэтому a2 +
b2 = c2.
c
b

16. «Спускаясь и поднимаясь» М.Эшер

Для сюжетов «классических» произведений
Эшера характерно остроумное осмысление
логических и пластических парадоксов

17. «Спускаясь и поднимаясь»

18.

Заключение
•Поиск заключенных в софизме ошибок, ясное понимание
их причин ведет к осмысленному изучению математики.
• Обнаружение и анализ ошибки, заключенной в софизме,
очень часто оказывается более поучительным, чем просто
разбор решений «безошибочных» задач.
• Эффектная демонстрация «доказательства»
явно
неверного результата, демонстрация того, к какой
нелепице
приводит
пренебрежение
каким-либо
математическим правилом, и последующий поиск и
разбор ошибки, позволяют понять и «закрепить»
математическое правило или утверждение.
Такой подход способствует пониманию того, что
математика – это живая наука, а не собрание закостенелых
догм, выдуманных по чьей-то злой воле.