Similar presentations:
Тригонометрические уравнения
1.
Тригонометрическиеуравнения
2. Определения тригонометрических функций
Синусом угла х называетсяордината точки
единичной окружности,
полученной из точки (1; 0)
поворотом на угол х
sin x
x
(1;0)
3.
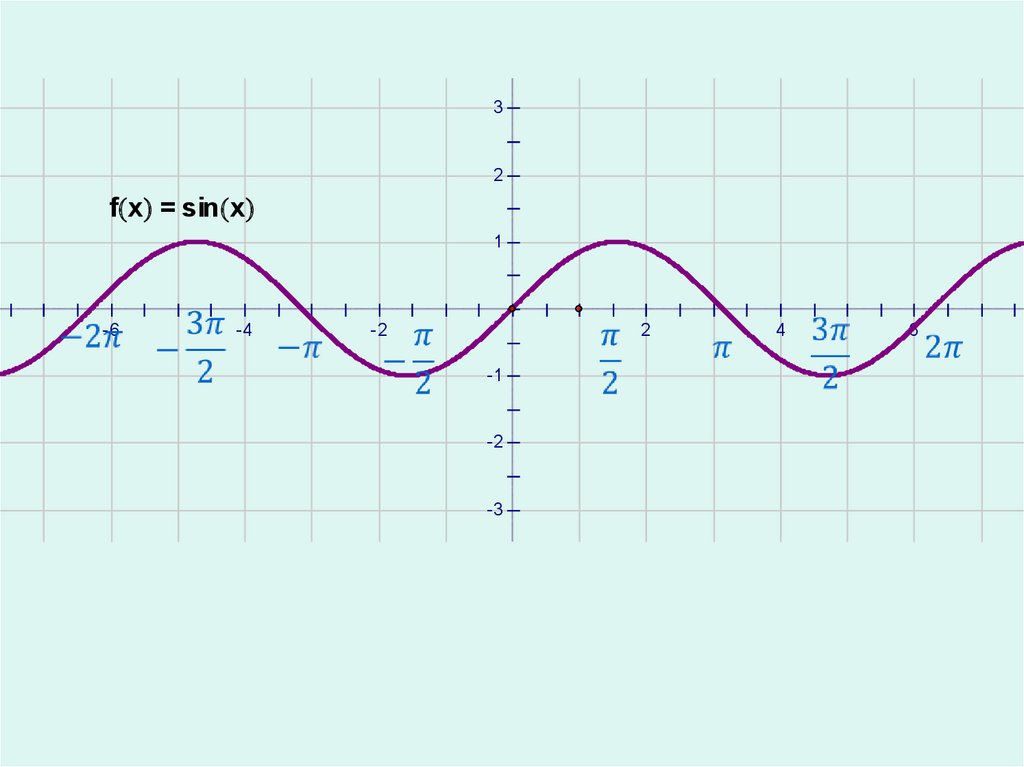
32
f x = sin x
1
-6
-4
-2
2
-1
-2
-3
4
6
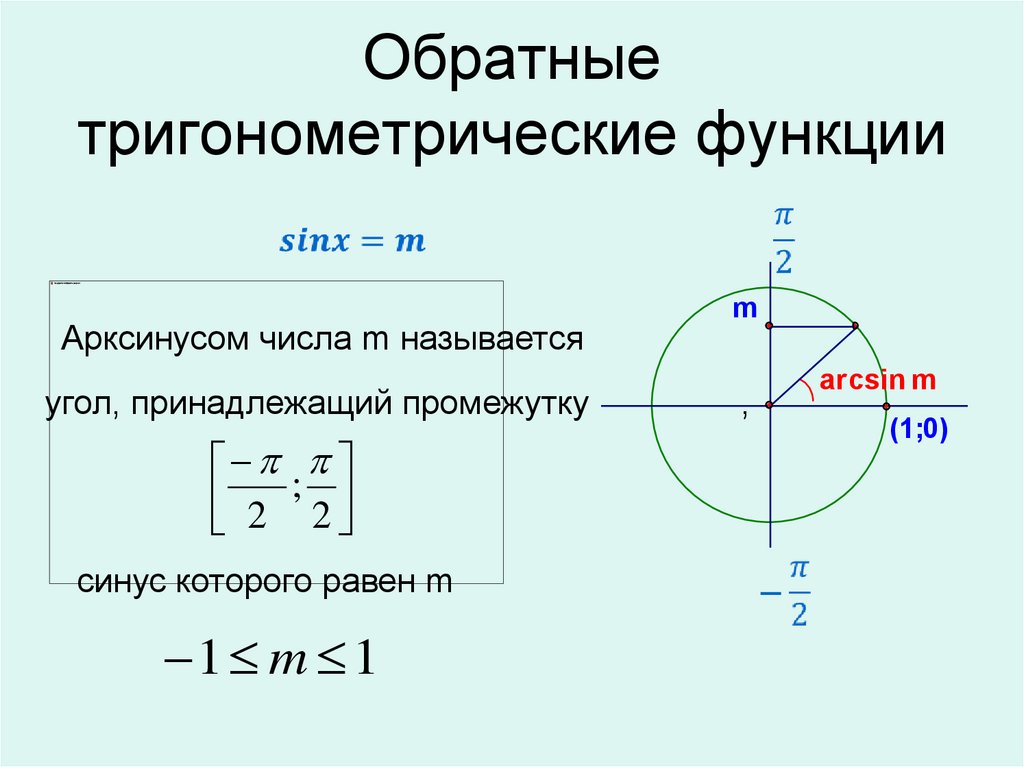
4. Обратные тригонометрические функции
Аркcинусом числа m называетсяугол, принадлежащий промежутку
2 ; 2
синус которого равен m
1 m 1
m
,
arcsin m
(1;0)
5. arcsin (-a)=-arcsin a
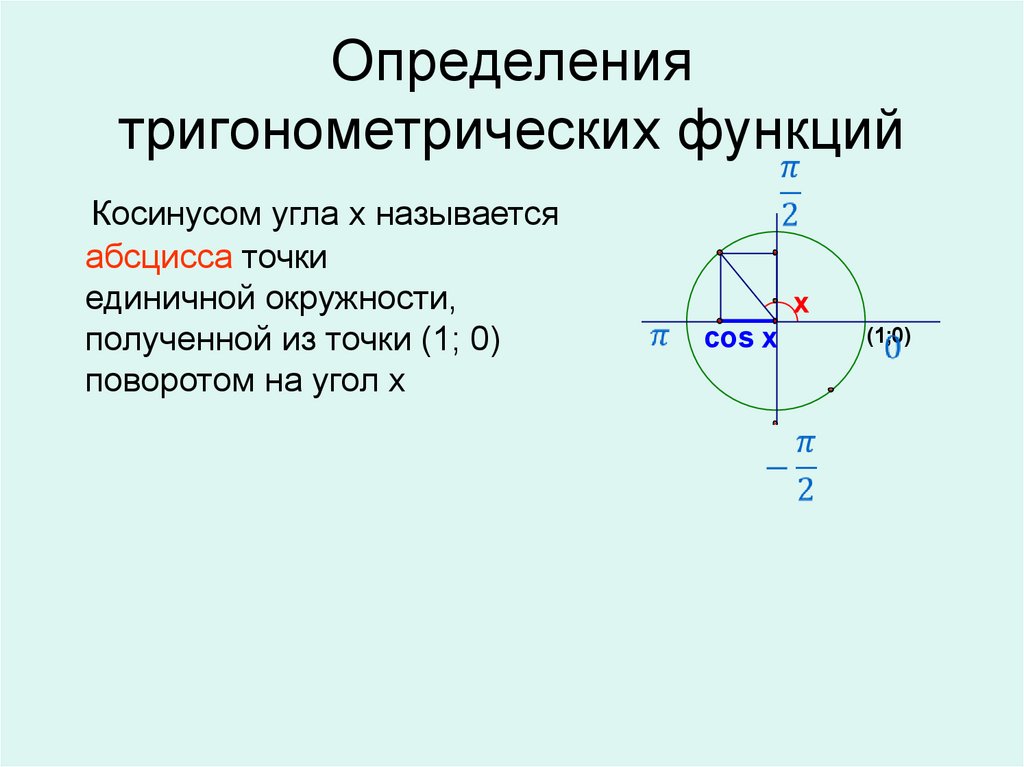
(1;0)6. Определения тригонометрических функций
Косинусом угла х называетсяабсцисса точки
единичной окружности,
полученной из точки (1; 0)
поворотом на угол х
x
cos x
(1;0)
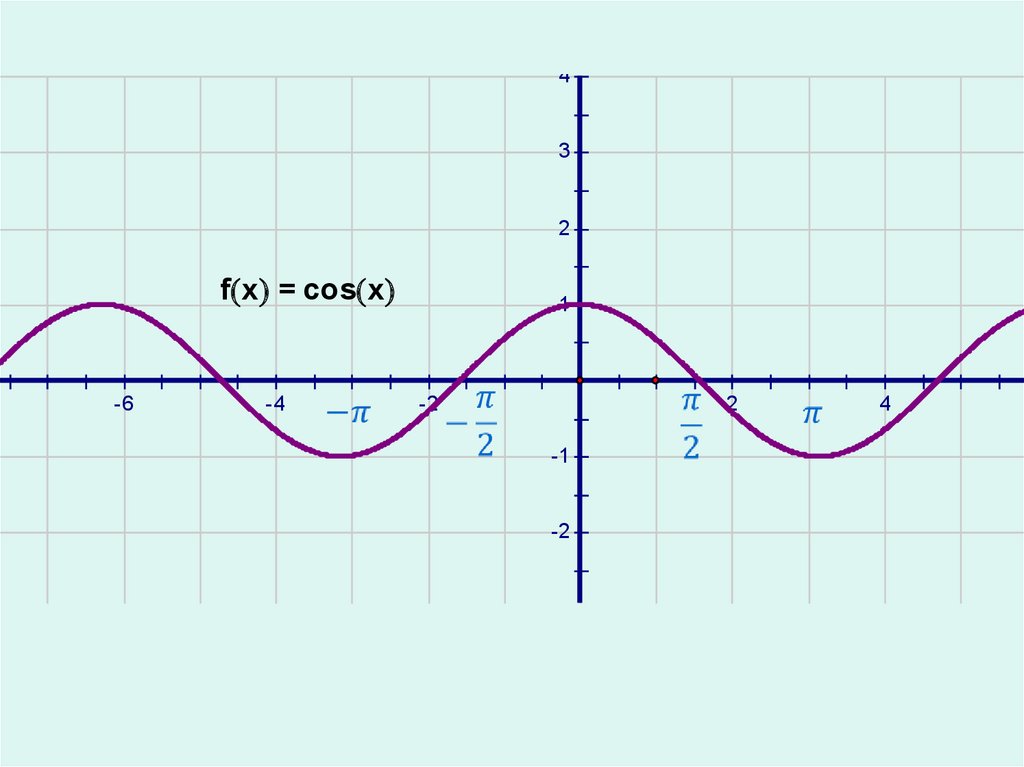
7.
43
2
f x = cos x
-6
-4
1
-2
2
-1
-2
4
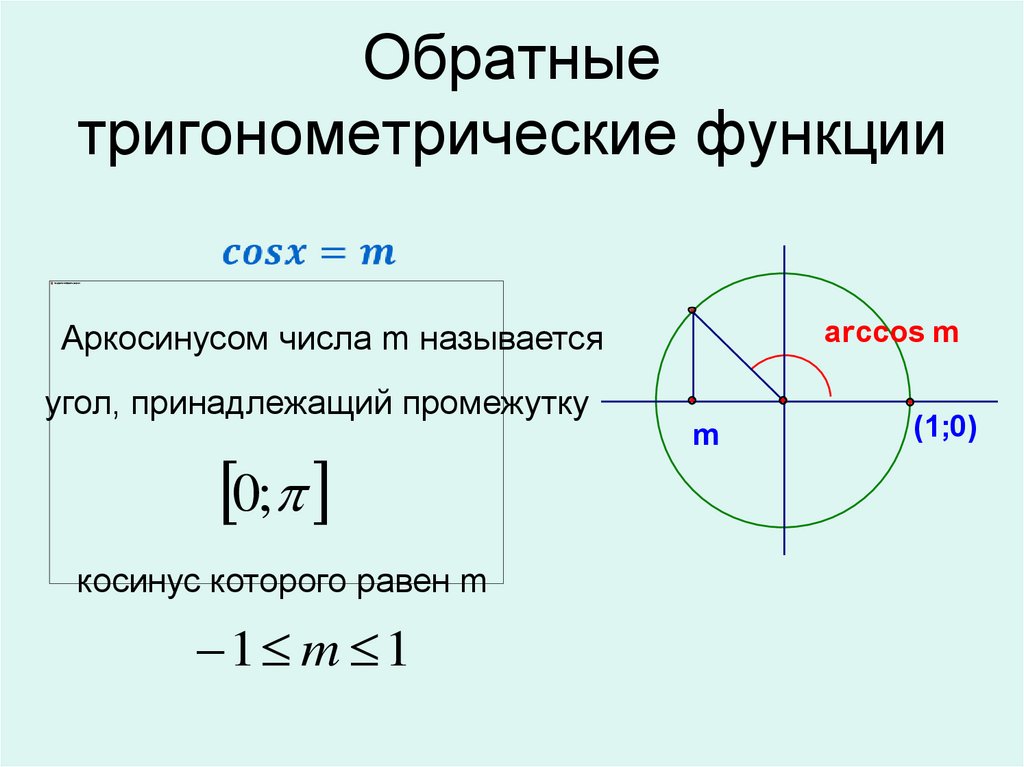
8. Обратные тригонометрические функции
Аркосинусом числа m называетсяarccos m
угол, принадлежащий промежутку
0;
косинус которого равен m
1 m 1
m
(1;0)
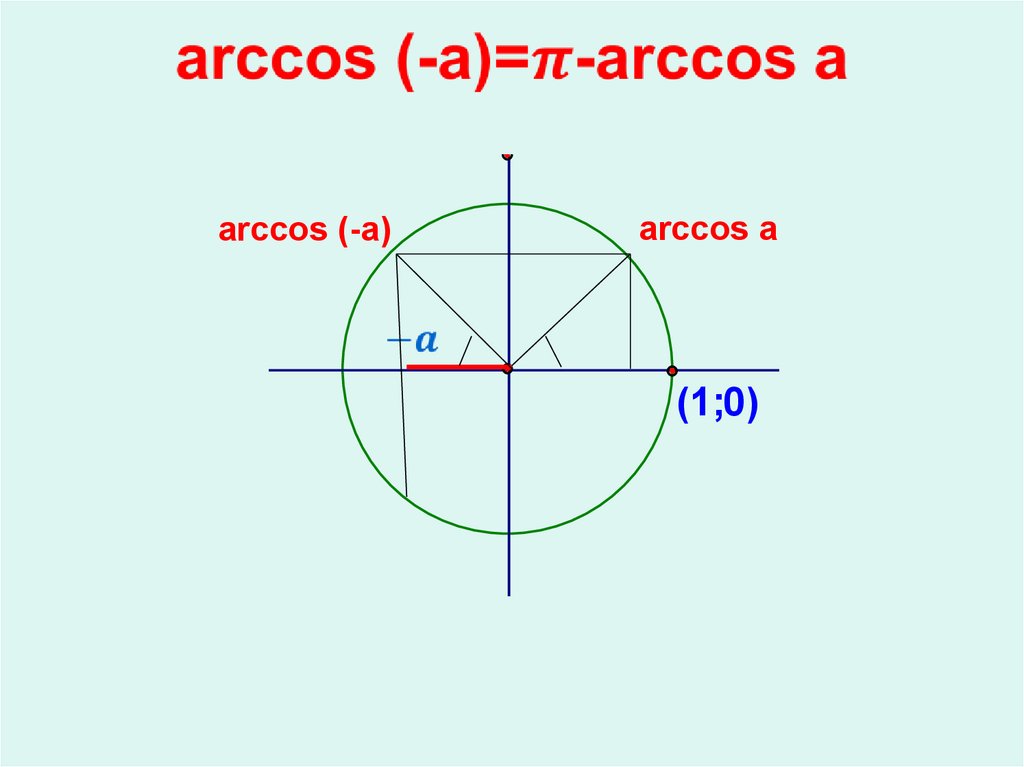
9.
arccos (-a)arccos a
(1;0)
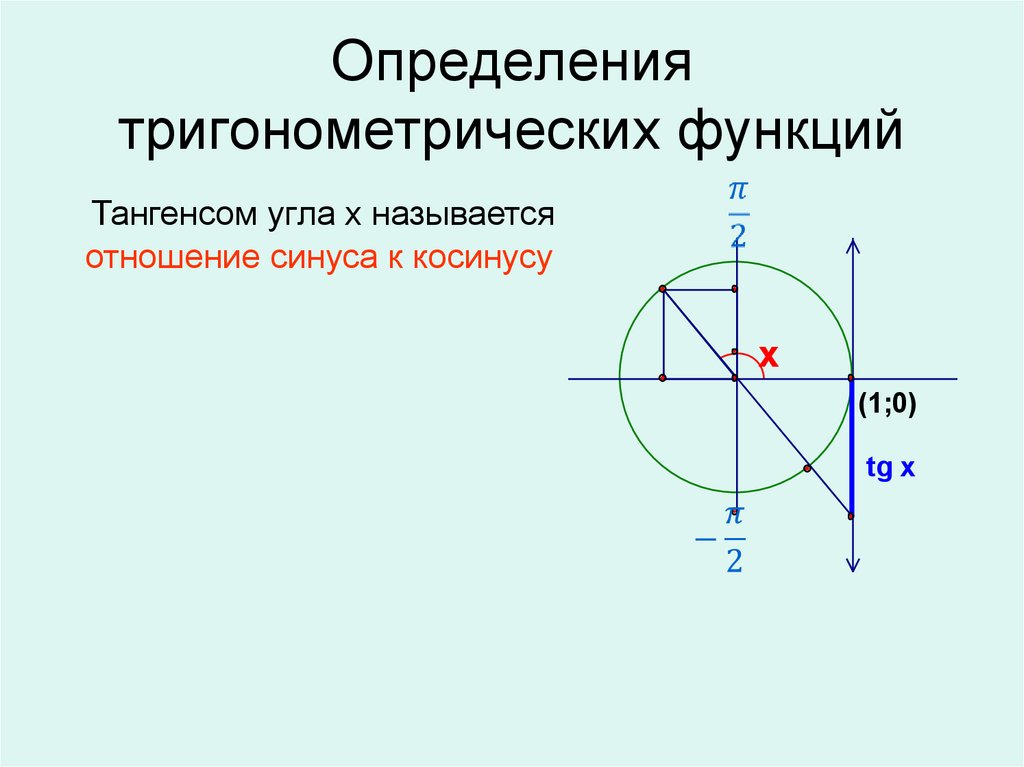
10. Определения тригонометрических функций
Тангенсом угла х называетсяотношение синуса к косинусу
x
(1;0)
tg x
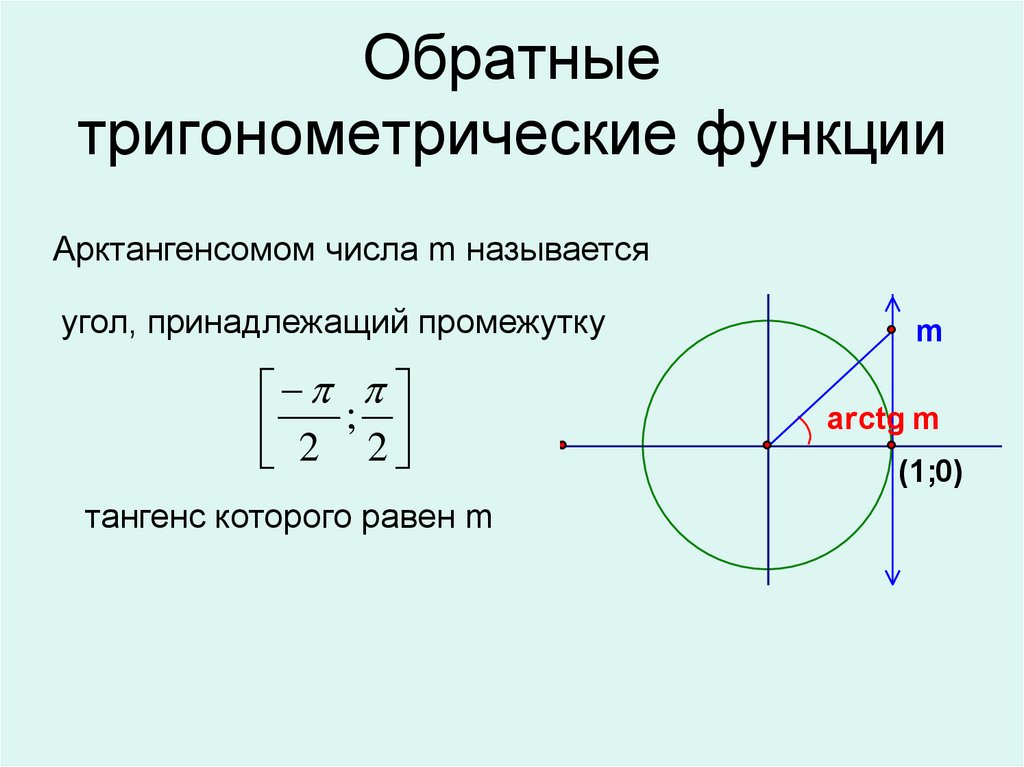
11. Обратные тригонометрические функции
Арктангенсомом числа m называетсяугол, принадлежащий промежутку
2 ; 2
тангенс которого равен m
m
arctg m
(1;0)
12.
Решение простейших уравненийРешим уравнение
sin x 0
(1;0)
13.
Решение простейших уравненийРешим уравнение
sin x 1
(1;0)
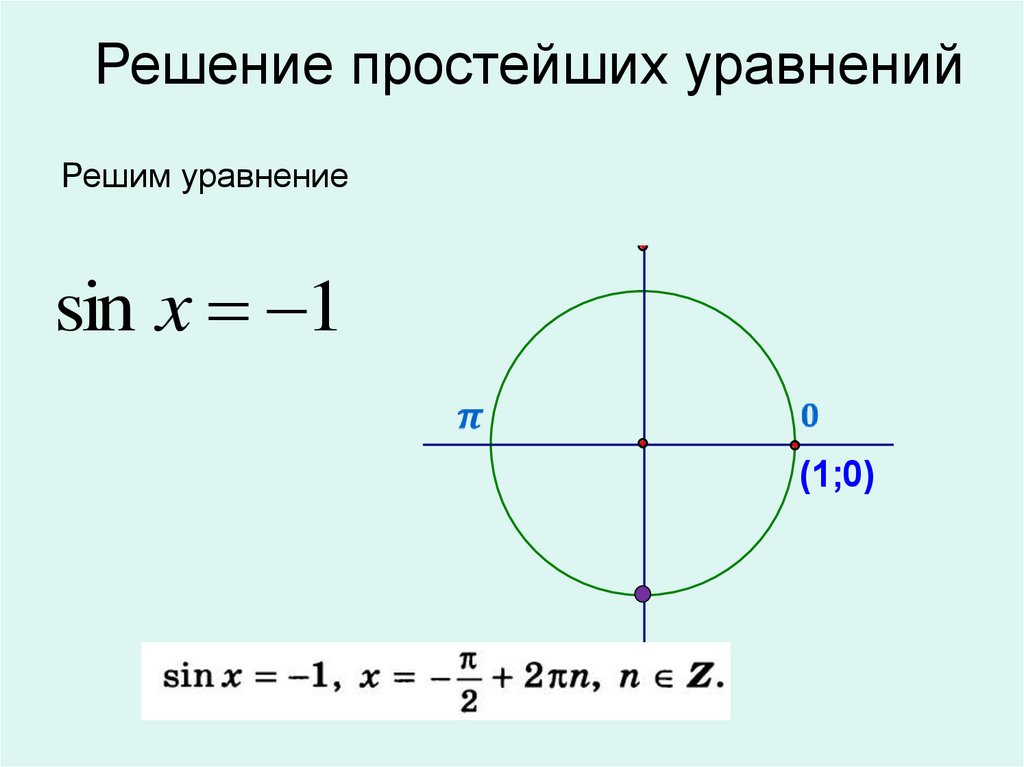
14.
Решение простейших уравненийРешим уравнение
sin x 1
(1;0)
15.
Решение простейших уравненийРешим уравнение
cos x 0
(1;0)
16.
Решение простейших уравненийРешим уравнение
cos x 1
(1;0)
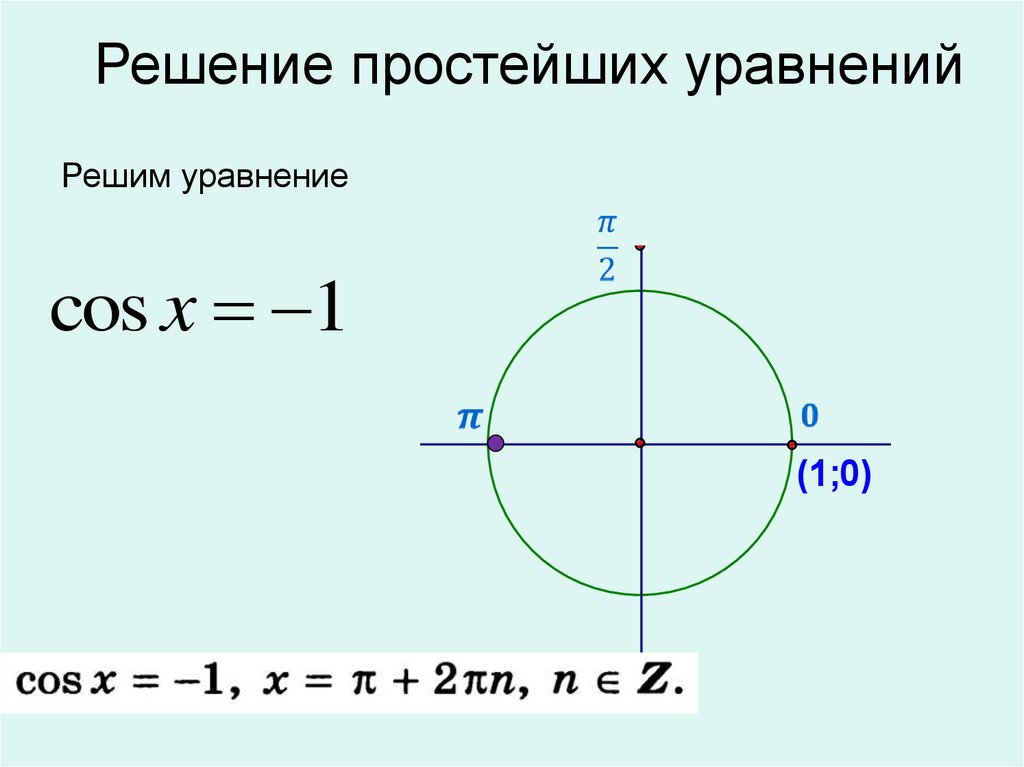
17.
Решение простейших уравненийРешим уравнение
cos x 1
(1;0)
18.
Решение простейших уравненийРешим уравнение
3
sin x
2
(1;0)
19.
32
f(x)=a
-6
f x = sin x
-4
1
-2
2
-1
-2
-3
4
6
8
20.
Решение простейших уравненийРешим уравнение
cos x а
x
a
(1;0)
21.
Решение простейших уравненийРешим уравнение
1
3
2 sin x 2
2
4
1
2
3
sin x
2
2
4
2
2
(1;0)
n
1
2
3
2 n, n Z
x 1 arcsin
2
2
4
1
3
1 3
3
2 n, n Z x
2 n, n Z
x
2 4
2
4
4
4
22.
23.
(1;0)(1;0)
24. Чтобы отобрать корни, принадлежащие отрезку , решим двойное неравенство относительно k
Чтобы отобрать корни, принадлежащие отрезкурешим двойное неравенство относительно k
,















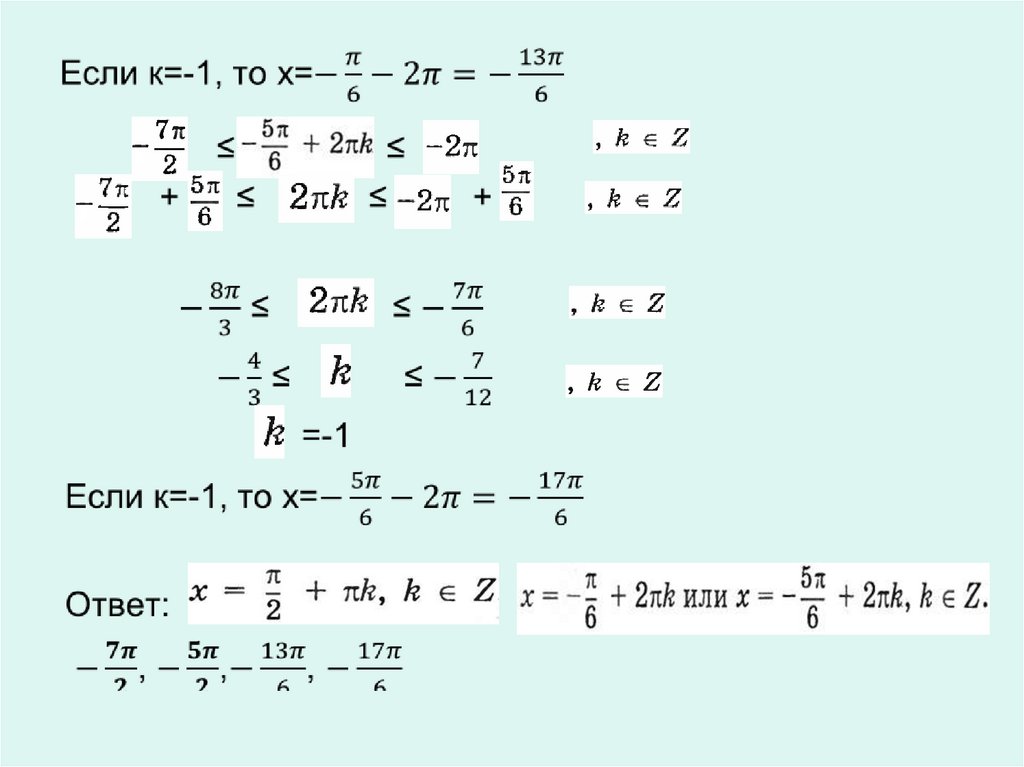
 mathematics
mathematics








