Физическая экология. Глобальная климатическая модель

1. Физическая экология

Занятие 11
Глобальная климатическая
модель

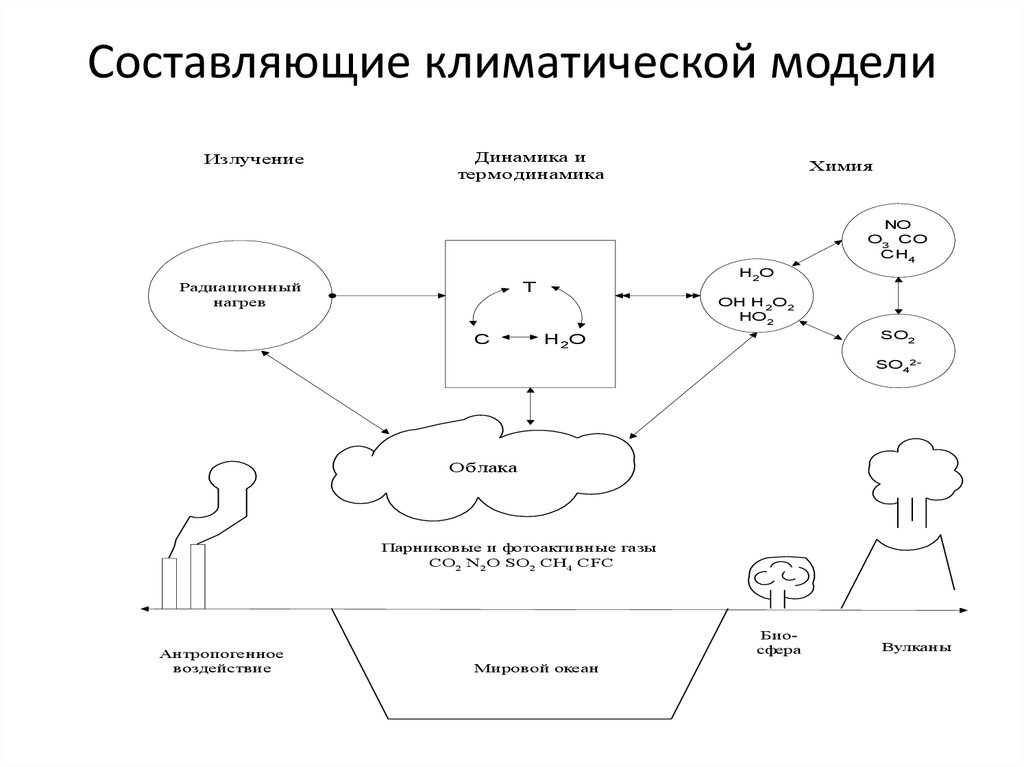
2. Составляющие климатической модели

Излучение
Динамика и
термодинамика
Химия
NO
O3 CO
CH4
Радиационный
нагрев
H2O
T
OH H 2O2
HO 2
C
SO2
H 2O
SO42-
Облака
Парниковые и фотоактивные газы
CO2 N 2O SO2 CH4 CFC
Антропогенное
воздействие
Биосфера
Мировой океан
Вулканы

3.

Качественный анализ климатической системы
В простейшем линейном анализе климата факторы, выводящие
систему из стационарного состояния, характеризуются как
возмущения. Полное возмущение равно алгебраической сумме
всех изменений подводимого к Земле энергетического потока.
Относительная величина возмущения обознается «дельта Q».
Результирующее воздействие может быть положительным и
привести к потеплению, может быть также отрицательным и
привести к охлаждению. Линейный коэффициент модели,
определяющий изменение температуры системы «дельта T»,
называют чувствительностью климата, он обозначается
греческой буквой λ и имеет размерность (K∙м2)∙Вт-1
T Q

4.

Стационарное состояние
Пусть Fп и Fа – это поток мощности, идущий от поверхности и
проходящий через атмосферу, соответственно.
Fп Tn ,
4
Fa Ta .
4
Вводя обозначения для солнечной постоянной S, альбедо α и парникового
коэффициента ε, можно записать систему двух стационарных уравнений
2Fa Fn 0
S
Fn Fa 1 .
4
При подстановке известного из опыта значения 288 К получаем вероятные
значения для альбедо 0,33 и парникового коэффициента 0,83.
S (1 )
Tп
4 (1 )
2
1
4

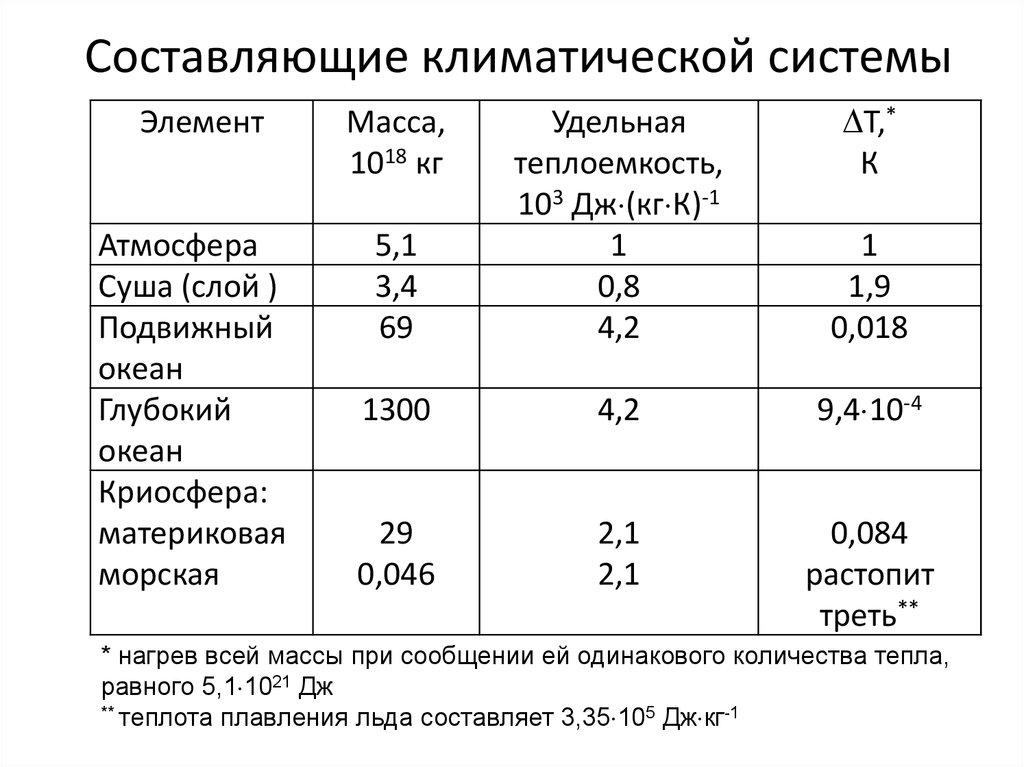
5. Составляющие климатической системы

Элемент
Масса,
1018 кг
Атмосфера
Суша (слой )
Подвижный
океан
Глубокий
океан
Криосфера:
материковая
морская
Т,*
К
5,1
3,4
69
Удельная
теплоемкость,
103 Дж (кг К)-1
1
0,8
4,2
1
1,9
0,018
1300
4,2
9,4 10-4
29
0,046
2,1
2,1
0,084
растопит
треть**
* нагрев всей массы при сообщении ей одинакового количества тепла,
равного 5,1 1021 Дж
** теплота плавления льда составляет 3,35 105 Дж кг-1

6.

Нульмерная балансовая модель
Рассмотрим случай малого отклонения от стационарной температуры,
вызванного возмущением поступающего на Землю теплового потока ΔQ(t).
Пусть результирующее малое отклонение поверхностной температуры от
стационарного значения выражается как
T (t ) T (t ) Tn .
Уравнение теплового баланса в дифференциальной форме, отнесенное к
единичной площади поверхности, запишется в виде:
d T (t )
c
T Q,
dt
где с – теплоемкость, а λ – множитель обратной связи, учитывающий
стабилизирующие и дестабилизирующие реакции системы в ответ на
возмущение, его знак критическим образом определяет прогноз поведения
системы. К примеру, увеличение атмосферного содержания углекислого газа
от 275 до 475 миллионных долей, прогнозируемое от промышленной
деятельности к 2030 г., соответствует ΔQ(t) = 3,5 Вт∙м-2.

7.

Одномерная климатическая модель
Разделим океан на верхний перемешиваемый слой и глубокие слои.
Верхний слой глубиной порядка 70 м имеет теплоемкость
cn c p h 8,3 108 Дж(м2∙К)-1
и за счет быстрого перемешивания волнами поддерживается при
одинаковой температуре.
Для глубокого океана перенос тепла от поверхности происходит
вместе с переносом вещества и описывается уравнением:
T ( z, t )
2T ( z, t )
T ( z, t )
D
(
z
)
t
z 2
t
D – это коэффициент диффузии, составляющий примерно 1,3 см2∙с-1,
а ω(z) – скорость вертикальных движений.

8.

Одномерная климатическая модель: решение
Для глубокого океана адвекцией, т. е. переносом вещества направленным
движением, можно пренебречь:
2
d T ( z) T ( z)
2
D 0
dz
Используем приближение быстрого по сравнению со временем диффузии
обмена с характерным временем τ0 ~ 33 года.
T0 ( z 0) Tп ; T ( z ) 0
z
T0 ( z ) Tп exp
D 0

9. Понятие прогноза

Пусть известна система уравнений вида
X i
Fi ( X 1 , X 2 ... X i , t )
t
где Xi – полный набор макроскопических климатических
переменных. Пусть, также, система снабжена начальными
условиями. По теореме Коши при достаточно мягких ограничениях
на функции Fi (ограниченность и кусочная непрерывность) решение
системы существует и является единственным. Это единственное
решение – прогноз климатической системы.
Глобальная климатическая модель – это согласованная система
уравнений, включающую уравнения:
• сохранения,
• движения,
• переноса излучения и радиационно-теплового баланса,
• водяного пара,
• фотохимических реакций.
Эта система уравнений должна допускать аналитическое
или численное решение.

10. Динамика атмосферы: уравнения

Закон сохранения массы для элемента единичной массы:
d ( V )
0
dt
1 d
1 d ( V )
dt V dt
1 d
div( c )
dt
c -- это трехмерный вектор скорости
Уравнение движения для элемента среды единичной массы в
гравитационном поле (Навье-Стокса):
1
dc
2 c grad ( p) g F
dt
где = 7,3·10-5 с-1 – угловая скорость вращения Земли, F –
обобщенная объемная сила, например трение на границе
сред.

11. Динамика атмосферы: сила Кориолиса

Параметром Кориолиса называется
f 2 cos
Для средних широт по порядку величины он
составляет 10-4. Сила, действующая на
элемент среды единичной массы,
движущийся в направлении север-юг, равна
произведению его скорости на параметр
Кориолиса и в Северном полушарии
направлена вправо от направления движения.
Ro
f L
Число Россби, где υ и L – это
характерные скорость и масштаб
коллективного движения.
Кориолисова сила доминирует при
Ro << 1 и пренебрежимо мала при
Ro >> 1.

12. Динамика атмосферы: уравнения

dT Q cV
1 T div (c )
dt c p c p
p R T
Уравнение сохранения энергии в
форме теплового баланса. Q –
суммарный приток тепла к единице
массы за счет радиационного и
турбулентного теплообмена.
Уравнение состояния для сухого воздуха.
Здесь R – газовая постоянная для сухого воздуха,
сp – удельная теплоемкость воздуха при постоянном
давлении, сV – удельная теплоемкость воздуха при
постоянном объеме. Напомним, что для сухого
воздуха сV = 718 Дж∙кг-1 К-1, сp = 1066 Дж·кг-1 К-1.
R c p cV

13.

Динамика атмосферы: закономерности
В нижней атмосфере изменение давления воздуха с высотой z
уравновешивается гравитационной силой, т. е. выполняется условие
гидростатического равновесия:
dp
g
dz
Нижняя атмосфера характеризуется преобладанием конвективного
распределения энергии над ее радиационным переносом.
В земной атмосфере барическая и Кориолисова силы близки. Доказано, что
для крупномасштабных процессов с характерным размером ячейки
порядка 1000 км (10 градусов) ветровые потоки в свободной атмосфере
близки к геострофическим. Равновесие между барическим градиентом и
Кориолисовой силой в условиях поддерживаемого температурного
градиента экватор–полюс приводит к регулярному движению вдоль кругов
широты с запада на восток.

14.

Динамика атмосферы: проблемы
1. Нелинейность уравнения Навье-Стокса
dc c dr
c
divc
c c
dt t dt
t
2. Крупномасштабные движения
3. Подсеточные процессы

15. Структура циркуляции: ячейки Хэдли (Гадлея)

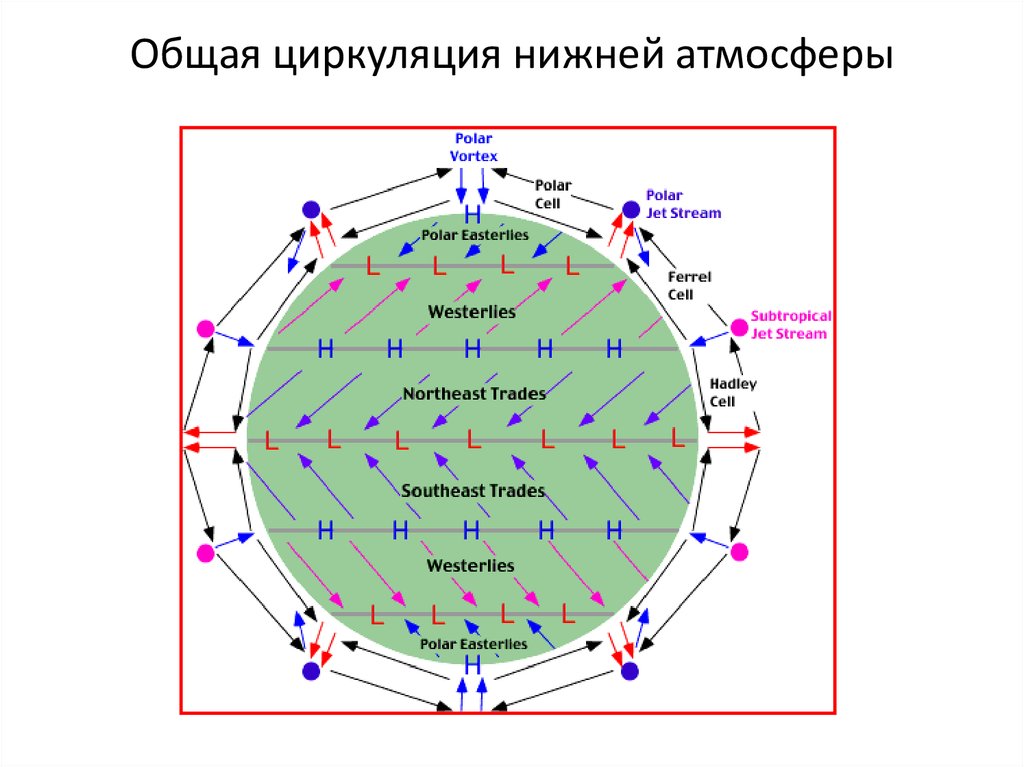
Джордж Хэдли (George Hadley, 1685 – 1768) – английский юрист

16. Общая циркуляция нижней атмосферы

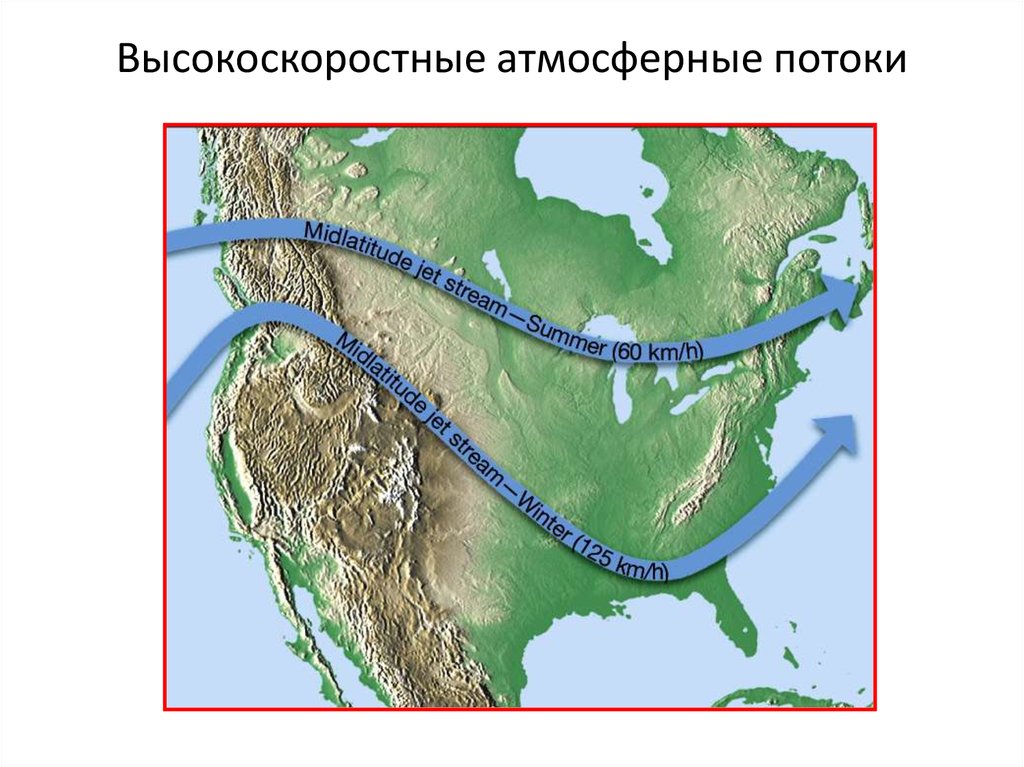
17. Высокоскоростные атмосферные потоки

18. Среднее состояние океана -- зима

19. Среднее состояние океана - лето

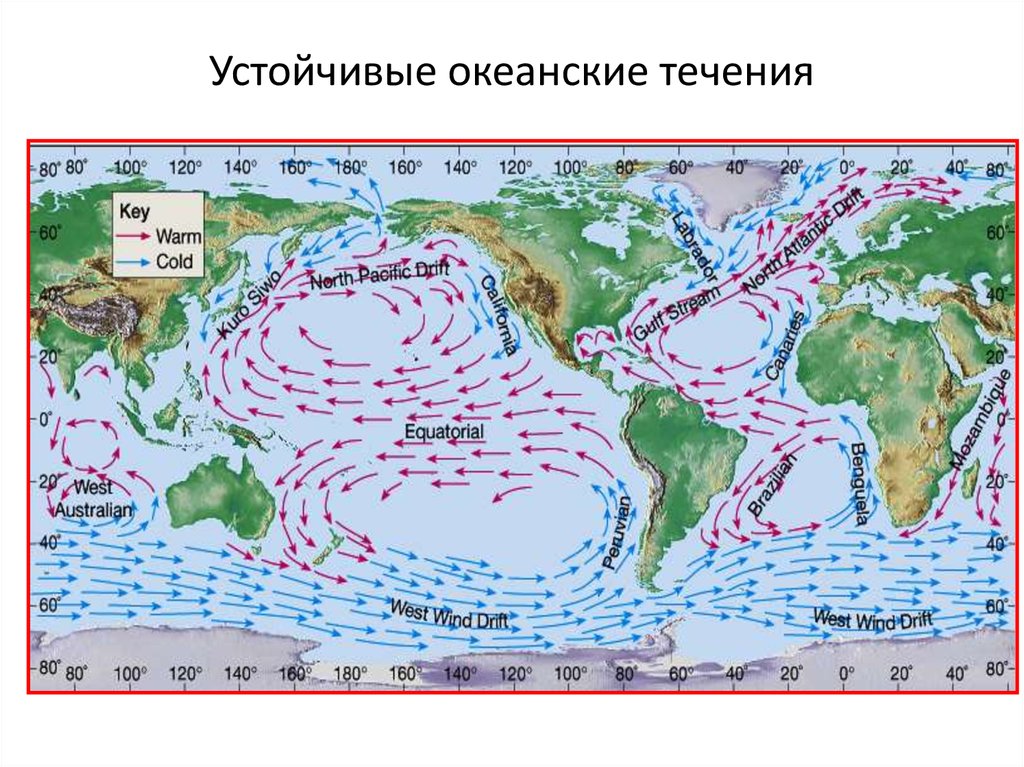
20. Устойчивые океанские течения

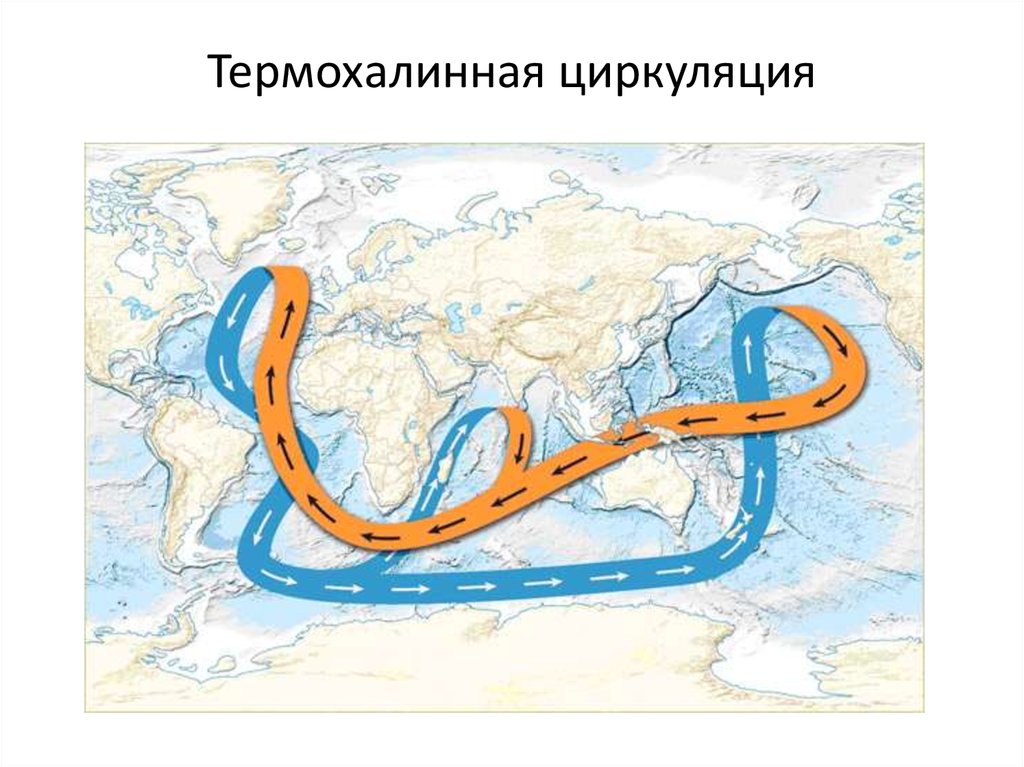
21. Термохалинная циркуляция

22.

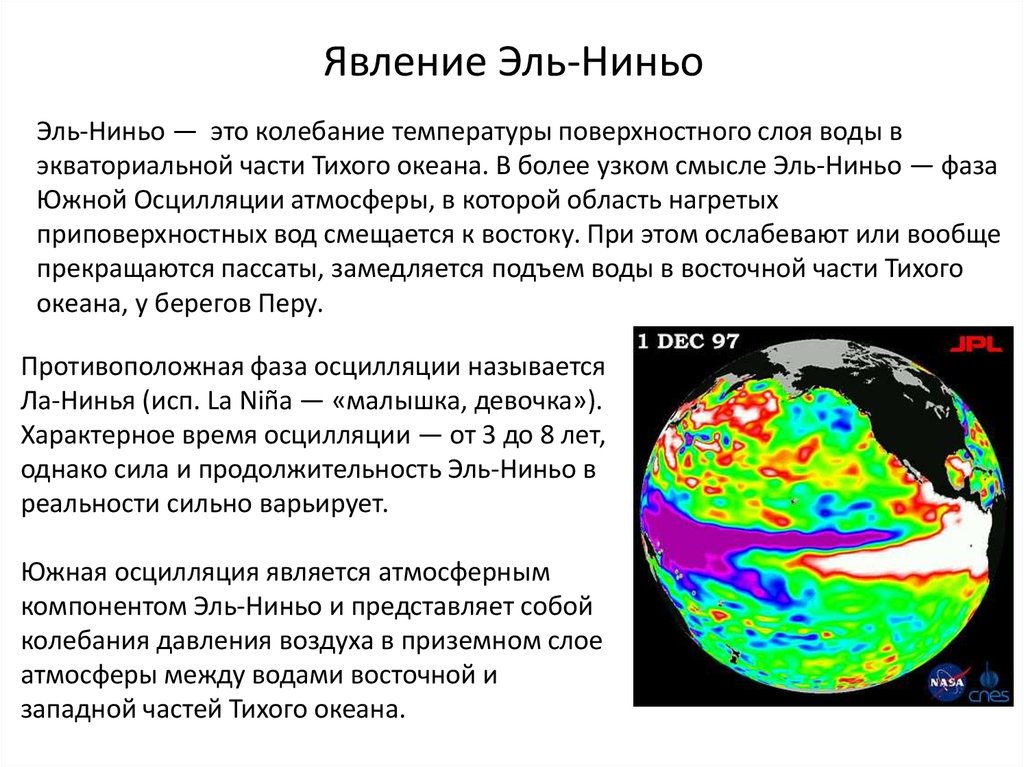
Явление Эль-Ниньо
Эль-Ниньо — это колебание температуры поверхностного слоя воды в
экваториальной части Тихого океана. В более узком смысле Эль-Ниньо — фаза
Южной Осцилляции атмосферы, в которой область нагретых
приповерхностных вод смещается к востоку. При этом ослабевают или вообще
прекращаются пассаты, замедляется подъем воды в восточной части Тихого
океана, у берегов Перу.
Противоположная фаза осцилляции называется
Ла-Нинья (исп. La Niña — «малышка, девочка»).
Характерное время осцилляции — от 3 до 8 лет,
однако сила и продолжительность Эль-Ниньо в
реальности сильно варьирует.
Южная осцилляция является атмосферным
компонентом Эль-Ниньо и представляет собой
колебания давления воздуха в приземном слое
атмосферы между водами восточной и
западной частей Тихого океана.

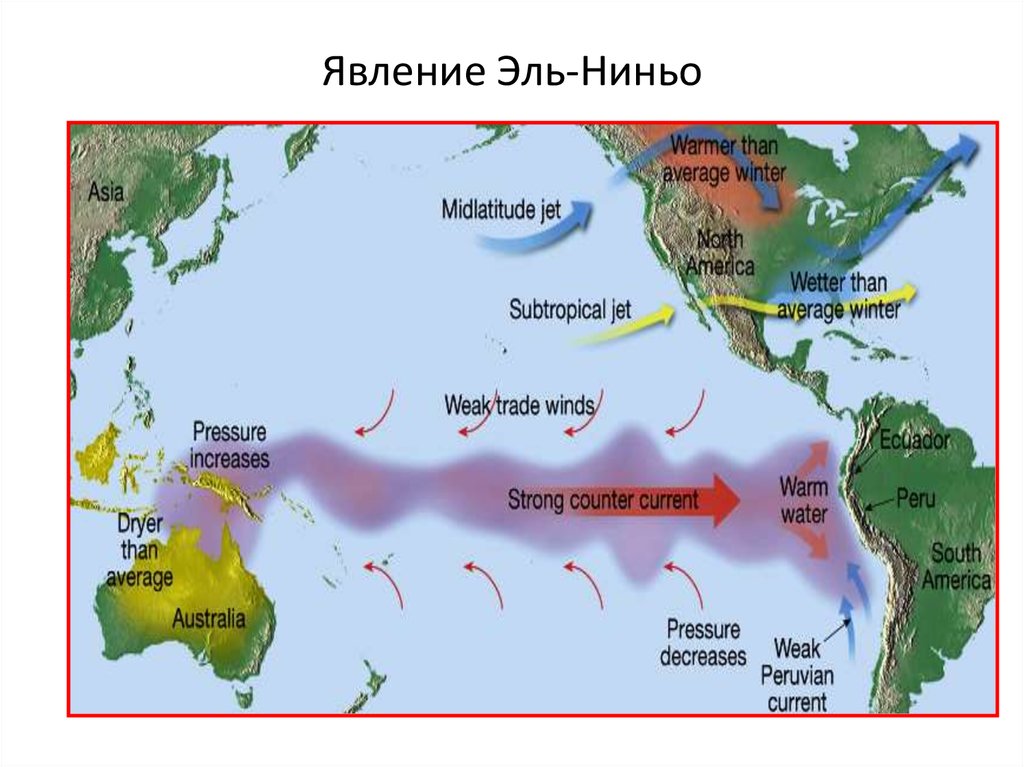
23. Явление Эль-Ниньо

24.

Явление Эль-Ниньо: мониторинг
Для прогноза Эль-Ниньо используются его признаки:
• повышение давления над Индийским океаном, Индонезией и Австралией
• падение давления над Таити, над восточной частью Тихого океана
• ослабление пассатов в южной части Тихого океана вплоть до их
прекращения
• теплая воздушная масса в Перу, дожди в перуанских пустынях.
Для описания Эль-Ниньо также
используется индекс Южной
осцилляции (SOI). Он вычисляется
как разность атмосферного
давлений над Таити и над
Дарвином (Австралия).
Отрицательные значения индекса
свидетельствуют о фазе Эль-Ниньо,
а положительные — о Ла-Нинья.

25.

Углеродообменная система