Similar presentations:
Исследование функций с помощью производной
1.
2. I.Проверка домашнего задания
Схематически построить график:1)y=
| ex 2 |
| x|
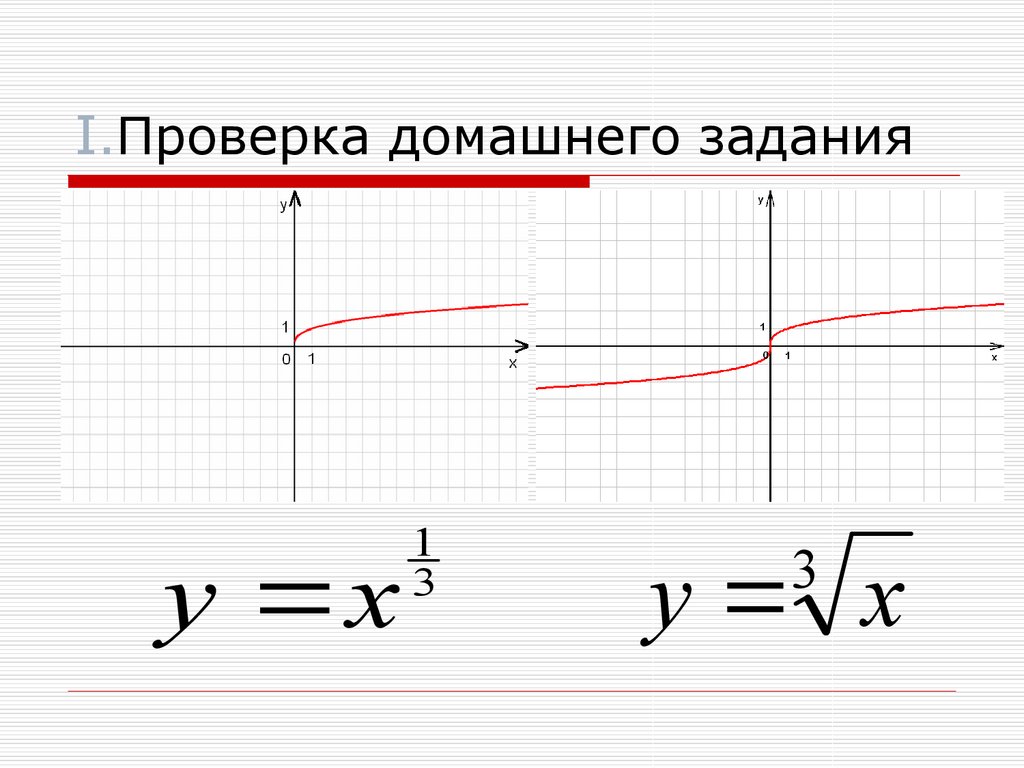
2)F(x)= ln
e
3)P(X)=
4)
3x;x 1
2
x 4; 1 x 2
lg (x 1 );x 2
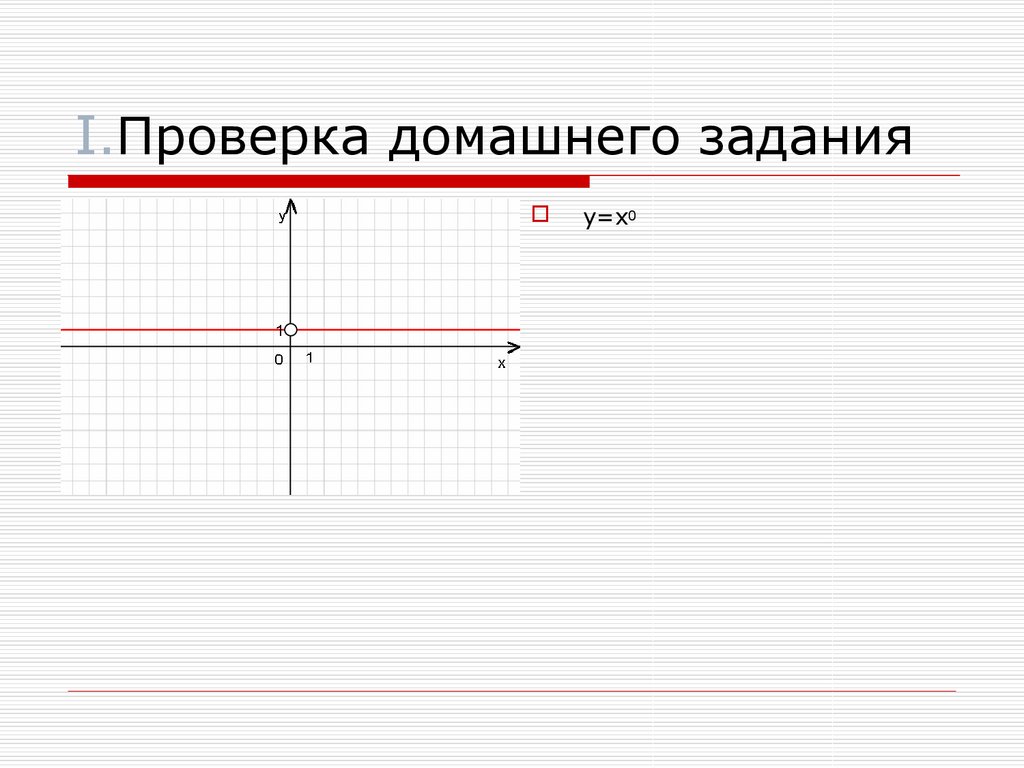
y x 0
1
3
5)
y x ; y 3 x
3
7)
1
y x 2 x 2
3. I.Проверка домашнего задания
y1
0 ln2
y |
e 2|
x
x
1.
2.
3.
4.
5.
6.
7.
y=l ex-2 l
D(y)=(-∞ ;+∞ )
E(y)=[0;+∞ )
Функция общего вида
y>0 (-∞ ;ln2)v(ln2;+∞ )
Функция возрастает – [ln2;+∞ )
Функция убывает – (-∞ ;ln2]
Точка минимума X=ln2
4. I.Проверка домашнего задания
1y ln |
x|
y
1. D(y)=(-∞;0)U(0;+ ∞)
2. E(y)=(-∞;+ ∞)
3. Чётная функция
1
0
| x|
e
2) y ln | x | 1
1) y ln
1
x
5. I.Проверка домашнего задания
3x ; x 1p(x)= x 2 4 ; 1 x 2
lg( x 1); x 2
y
1
0 1
x
6. I.Проверка домашнего задания
y=x07. I.Проверка домашнего задания
1y x 3
y x
1
3
3
y x
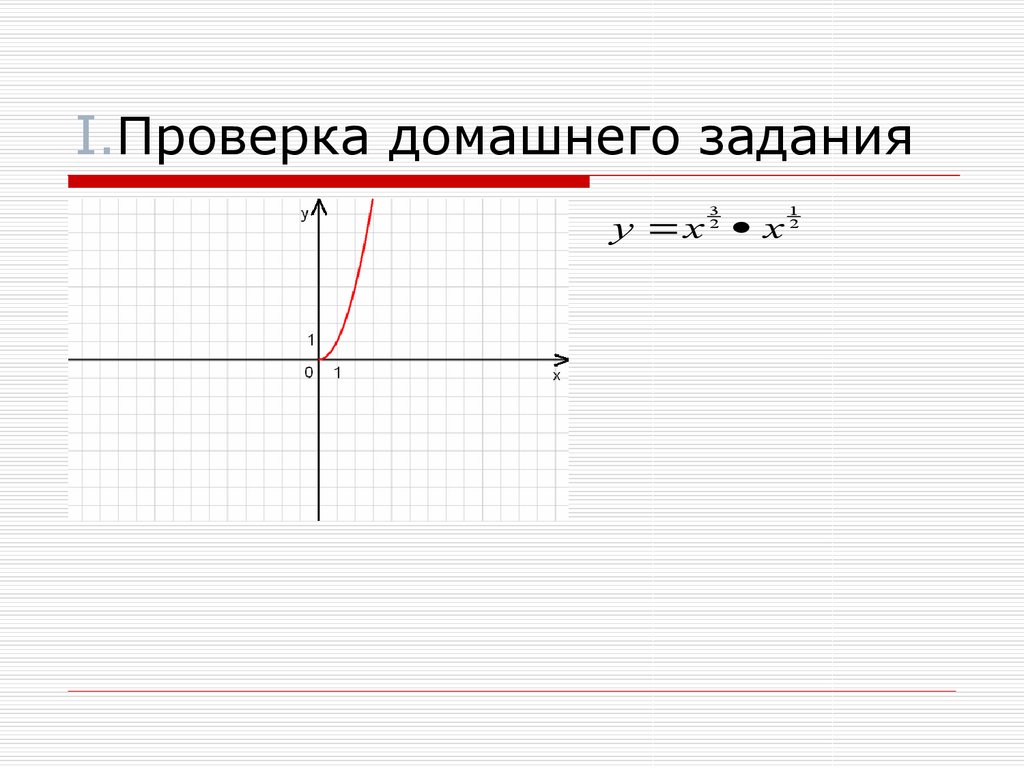
8. I.Проверка домашнего задания
32
y x x
1
2
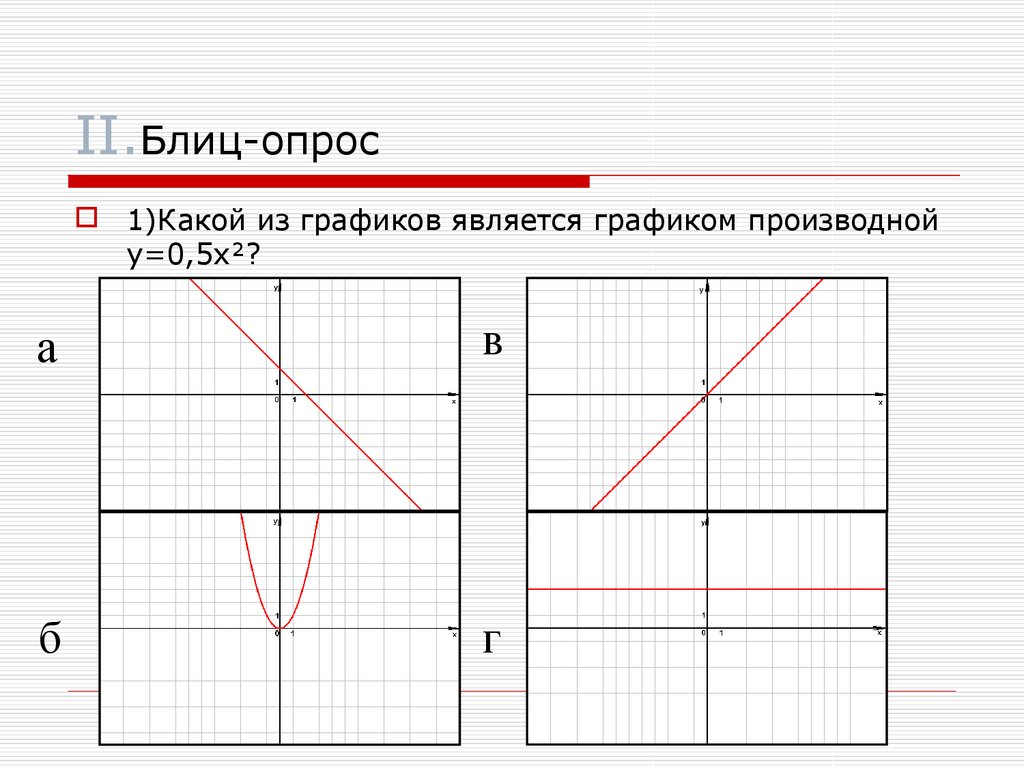
9. II.Блиц-опрос
1)Какой из графиков является графиком производнойy=0,5x ?
а
в
б
г
10. II.Блиц-опрос
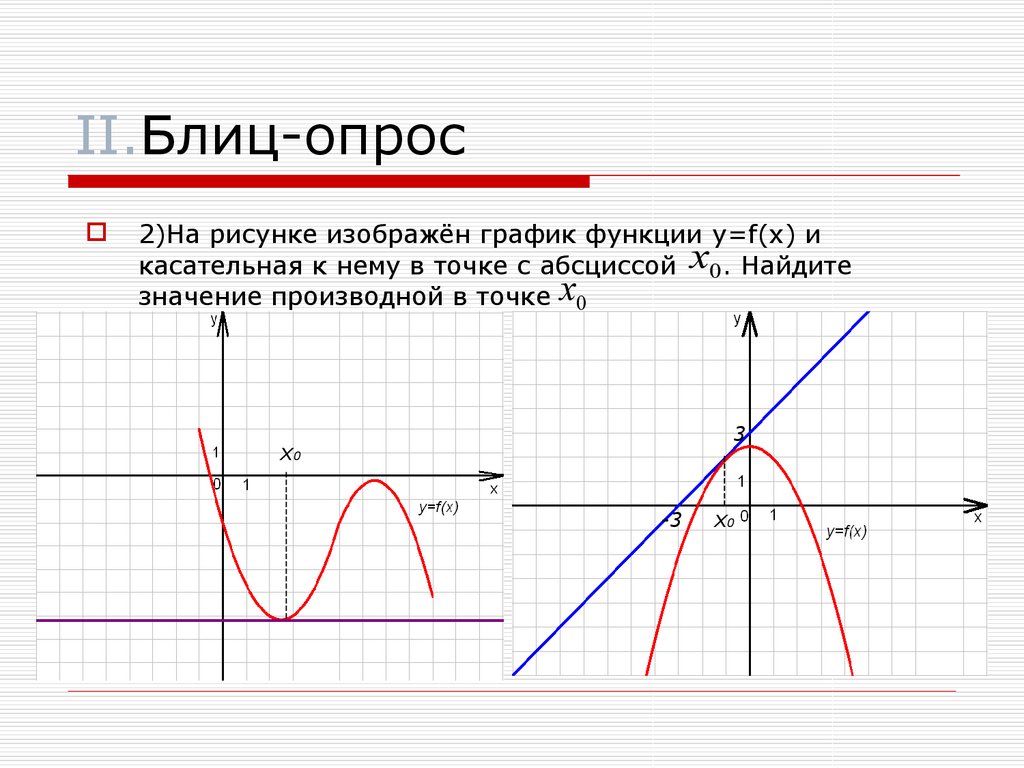
2)На рисунке изображён график функции y=f(x) икасательная к нему в точке с абсциссой x0. Найдите
значение производной в точке x0
3
x0
-3
x0
11. II.Блиц-опрос
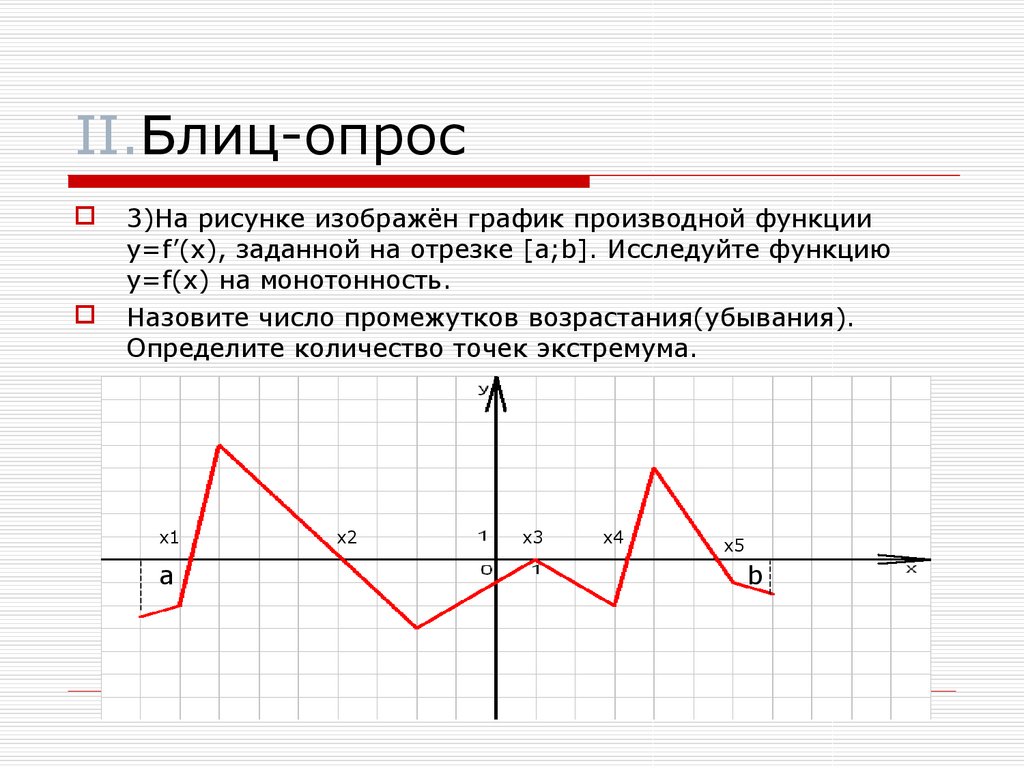
3)На рисунке изображён график производной функцииy=f’(x), заданной на отрезке [a;b]. Исследуйте функцию
y=f(x) на монотонность.
Назовите число промежутков возрастания(убывания).
Определите количество точек экстремума.
x1
a
x2
x3
x4
x5
b
12. II.Блиц-опрос
1)Производная некоторой функции f на всей числовойпрямой равна 0. Какой формулой следует задать функцию
f, если её график проходит:
а)через точку М (1;5)
б)через точку N (5;1) ?
2)Какие из указанных функции возрастают (убывают) на
множестве R:
3
f ( x) x 4 x 5
1
f ( x)
x
f ( x) 3x 4
3
f ( x) 4 x ?
13. II.Блиц-опрос
На рисунке показан график функции f(x)y
1
0
1
Сколько экстремумов имеет функция y=|f(x)|?
x
14. I I I. Творческое задание: Отыщите функцию в таблице, исходя из её «автобиографии».
Я, функция сложная, этоизвестно,
Ещё расскажу, если вам
интересно…
Что точку разрыва и корень
имею,
И есть интервал, где расти не
посмею.
Во всём остальном
положительна, право,
И это конечно не ради забавы.
Для чисел больших я стремлюсь
к единице,
Найди меня среди прочих в
таблице.
1 4
x
4
1
1 2
x3
x 2x 3
3
2
x 1
x 1
2x
x2 x
1
3 4x2
1) f ( x )
2) f ( x )
3) f ( x )
4) f ( x )
5) f ( x )
2
x 2
6) f ( x )
x 2
7 ) f ( x ) ( x 2 1) 3
8) f ( x ) x (1 x )
x
9) f ( x ) 2
x 1
15. IV.Самостоятельная работа
Дана функция:2
x
f ( x) 2 x
2
2
1)Найдите f’(x)
2)Постройте график y=f’(x)
3)Опишите свойство функции y=f(x), указывая промежутки
монотонности и точки экстремума, заполните таблицу
x
f’(x)
f(x)
4)Постройте график функции y=f(x), исследуя график функции
y=f(x) убедитесь в правильности заполнения таблицы.
5)Постройте касательную к графику функции в его точке с
абсциссой x0 2 , напишите уравнение касательной.
16. IV. Самостоятельная Работа
Дана функция:2
x
f ( x) x
2
2
1)Найдите f’(x)
2)Постройте график y=f’(x)
3)Опишите свойство функции y=f(x), указывая промежутки
монотонности, и точки экстремума, заполните таблицу
x
f’(x)
f(x)
4)Постройте график функции y=f(x), исследуя график функции
y=f(x) убедитесь в правильности заполнения таблицы.
5)Постройте касательную
к графику функции в его точке с
x0 1
абсциссой
, напишите уравнение касательной.
17. V. Домашнее задание
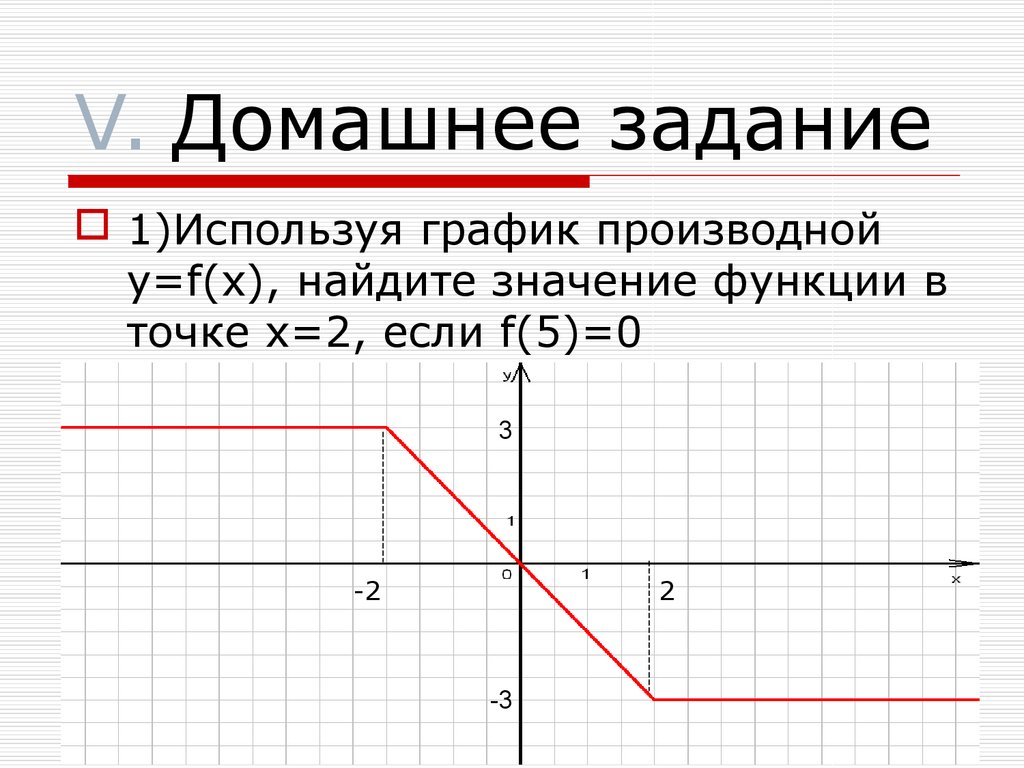
1)Используя график производнойy=f(x), найдите значение функции в
точке x=2, если f(5)=0
3
-2
2
-3
18. V. Домашнее задание
2)Определить, при каком значениипараметра максимум функции
равен 3?
2b 1
y 4
x 1











 mathematics
mathematics








