Similar presentations:
Решение нестандартных задач в рамках итогового повторения курса алгебры и начала анализа
1. Урок – смотр знаний
УРОК – СМОТР ЗНАНИЙВ 11 классе
ГОУ Гимназии №63
Калининского района
Санкт-Петербурга
Учитель: Залыгина Т.И.
2. Тема урока:
ТЕМА УРОКА:«Решение нестандартных задач в рамках
итогового повторения курса алгебры и
начала анализа»
3. цели:
ЦЕЛИ:- образовательная: повторение, обобщение и
систематизация знаний за 10-11 классы по
данным темам;
- воспитательная: воспитание толерантности и
ответственности;
-развивающая: умение собирать,
анализировать и систематизировать
информацию, объяснять сложные ключевые
моменты, находить нестандартные решения.
4. Задание № 1
ЗАДАНИЕ № 1Решить уравнение :
5 2 6 5 2 6
x
x
10
5.
Решение:Уравнения, решаемые заменой неизвестного.
5 2 6 5 2 6
x
x
10
Основания – иррациональные выражения, произведение которых равно 1:
5 2 6 5 2 6 = 1
ВАЖНО!
Выражения
5 2 6 и 5 2 6
называются сопряженными
6.
5 2 66
х
1)
Домножим каждый член уравнения на
Получим:
2) Обозначим
5 2 6 + 1 = 10 5 2
5 2 6 = t>0
2х
х
3) умножим это уравнение на t
1
,получим уравнение t 10
t
Получим: t2-10t +1=0 , получаем t1, 2
1.
=
х
2.
5 2 6
5 2 6 5 2 6
5 2 6 5 2 6Ответ
:x
х
=
х
х=1
х = -1
1
1, x2 1
7. Задание № 2
ЗАДАНИЕ № 2Решить неравенство :
2 x 3
log 0, 6
2
x 1 1
x x 2
8.
Решение:Решение трансцендентных неравенств.
2 x 3
log 0,6
2
x 1 1
x x 2
Решение:
ОДЗ
+
2x 3
x 1
-
-1
0
+
1,5
9.
x x 2x x 2 = 0 D 0
1)
Докажем, что
2
положителен при любых значениях х.
2
a
0
ветви параболы вверх
у
х
0
следовательно, неравенство
x
2
выполняется при любых х из ОДЗ
x 2
0
10.
2) рассмотрим две системы неравенств:1) х2 - х + 2 > 1
log 0,6
2)
2х 3
>0
х 1
х2 - х + 2 < 1
log 0,6
Решим вторую систему
х2 - х + 2 < 1
2х 3
<0
х 1
у
х2 - х + 1 < 0
/ х2 - х + 1 = 0
D< 0, a > 0
0
х
ВАЖНО!
на множестве всех действительных значений х2 - х + 2 < 1 не
имеет решения, следовательно вторая система решений не имеет.
11.
Тогда рассмотрим систему (1)Система эквивалентна неравенству: log
2х 3
х 1 >0
0,6
2х 3
0<
<1
х 1
2х 3
>0
1)
х 1
2х 3
2)
<1 ;
х 1
решением этого неравенства является ОДЗ
2х 3 х 1
<0 ;
х 1
+
Ответ : 1,5;4
х 4
<0
х 1
+
-
-1
4
12. Задание № 3
ЗАДАНИЕ № 3Найти наибольший корень уравнения:
3
3
ctg
ctg
x 4
x
13.
Решение:3
3
ctg
ctg
x 4
x
Так как период функции f(x)=tgx равен π, то
аргументы левой и правой части равны с точностью
до πk, где k – целое. ОДЗ не находим, так как проще
сделать проверку.
3
3
k
x 4
x
:π
14.
33 kx
x 4
x
3x 3 kx x 4
3x 3x kx 12 4kx
2
15.
kx 4kx 12 02
2k 4k 12k
12
x
2 4
k
k
2
x принимает максимальное значение, когда
12
k
принимает минимальное значение, то есть,
когда k = -1, так как k – целое число
16.
x 2 16 2Ответ : x 2
17. Задание № 4
ЗАДАНИЕ № 4Найдите наименьшее значение периметра
прямоугольника со сторонами, параллельными осям
координат, и с диагональю ОМ, где О – начало
координат, а М – точка на графике функции
,
y 5 . 2 ln( 0,4 x 3)
8 x 9,8
18.
2( x y )Периметр прямоугольника равен
, т.к. его стороны параллельны
осям координат, а одна его вершина является началом координат.
8 x 9,8
получаем
, подставив эти крайние точки в функцию y 5 2 ln( 0,4 x 3)
5 2 ln 0,2 y 5 2 ln 0,32 ,
0,4 x 3 3
т.е.x 7,5 О.Д.З:
y 0
положителен, так как функция является непрерывно убывающей на данном
промежутке. Значит периметр можно записать в виде
2( x y)
.
Периметр минимален, значит необходимо найти минимум функции
на промежутке
8;9,8
2( x y) p
19.
Ищем производную функции p по x:2 * 0,4 0,8x 6 1,6 0,8x 7,6
p (2( x 5 2 ln( 0,4 3)) 2(1
;
0,4 3
0,4 x 3
0,4 x 3
,
,
находим нули производной:
0,8 x 7,6
0,4 x 3
x 9,5
x 7,5
Область определения
функции y: 0,4 x 3 3
x 7,5
Находим знаки производной методом интервалов, т.к.
производная непрерывна на своей области определения:
y
x 9,5 точка минимума функции
Нашли одну искомую сторону прямоугольника y
7,5
9,5
,
y 5 2 ln( 0,4 x 3)
y 5 2 ln( 0,4 * 9,5 3) 5 2 ln 0,8 5 ln 0,64
Периметр:
p 2(9,5 5 ln 0,64) 29 ln 0,4096
Ответ : pmin 29 ln 0,4096
- вторая сторона
20. Задание № 5
ЗАДАНИЕ № 5Найти все значения параметра a, при которых система
имеет хотя бы одно решение.
2
2
2
:
x 5 y 36a
2
2
2
x y 12 49a
21.
Решение:Уравнения, составляющие систему, являются уравнениями
окружностей
x 5 y 36a
2
2
2
x y 12 49a
2
2
2
R=6a, центр – (5;0)
R=7a, центр – (0;12)
22.
yA 12
0
B
5
x
Из прямоугольного треугольника OAB расстояние между
центрами окружностей по теореме Пифагора равно 13.
23.
Для того, чтобы система имела хотя бы одно решение,окружности должны иметь хотя бы одну общую точку, а
значит, сумма их радиусов должна быть не меньше
расстояния между центрами этих окружностей.
С другой стороны, при увеличении параметра a одна
окружность полностью войдет в другую, поэтому радиус
большей окружности должен быть не больше суммы радиуса
меньшей и расстояния между центрами.
y
A
0 B
x
6 a 7 a 13
7 a 6 a 13
24.
6 a 7 a 137 a 6 a 13
a 1
a 13
a ; 1 1;
a 13;13
Ответ : a 13; 1 1;13
25. Задание № 6
ЗАДАНИЕ № 6Даны два уравнения.
log 7 ( x(12 p )) p( p 1) 6x 3
25 x 2 (5 p 3) x 15 Параметр р выбирается так, что p 0, p 1
2x
x
x( p 1)
и число различных корней уравнения в сумме с числом p+5 дает
число различных корней второго уравнения. Решите первое
уравнение при каждом значении параметра, выбранным таким
образом
26.
Решение:1) так как 12 p 0, то функция y log 7 ( x(12 p )) определена на
промежутке
(0; ) . Так как основание логарифма больше 1, то эта
функция возрастает. Линейная функция
убывает, так как коэффициент при х отрицателен. Поэтому число n корней
первого уравнения равно 0 или 1.
y p( p 1) 6 x 3
27.
2) С возрастанием х функцияy log 7 ( x(12 p ))
возрастает
неограниченно. При достаточно больших х ее график расположен выше
прямой
функции
y p( p 1) 6 x 3 . При приближении х к нулю значения
y log 7 ( x(12 p ))
неограниченно убывают, и ее
график окажется ниже этой прямой. Значит, прямая и график функции
пересекутся, т.е. n=1.
3) Число 0 не является корнем второго уравнения. При
уравнение равносильно уравнениям:
второе
x 0
25 x 2 (5 p 3) x 15
2x
x
x( p 1)
2
2
2 x ( p 1) 25( p 1) x (5 p 3) x 15
( 2 p 1) x 2 (5 p 3) x 5(5 p 8) 0
( x 5)(( 2 p 1) x (5 p 8)) 0( )
Уравнение (*) всегда имеет ненулевой корень x=-5. поэтому число k различных
корней второго уравнения равно 1 или 2.
28.
( x 5)(( 2 p 1) x (5 p 8)) 0( )4) По условию 1+(p+5)=k, т.е. p=k-6. Поэтому p=-5 или p=-4. Если p=-5,
то k=1, а уравнение (*) примет вид (x+5)(-9x+17)=0. у него два ненулевых
корня, т.е. k=2, что противоречит условию k=1. если p=-4, то k=2, а уравнение
(*) примет вид (x+5)(-7x+12)=0. у него два ненулевых корня, т.е. k=2.
значит, p=-4 удовлетворяет условию задачи.
5) При p=-4 первое уравнение примет вид
log 7 (14 x) 23 6 x
Его единственным корнем является число x=3,5, найденное подбором:
log 7 49 2,
23 21 2.
Ответ : x 3,5
29. Задание № 7(автор ученик 11 б класса морозкин илья, творческое задание в рамках спецкурса «Нестандартные задачи в курсе алгебры
ЗАДАНИЕ № 7(АВТОР УЧЕНИК 11 Б КЛАССА МОРОЗКИН ИЛЬЯ,ТВОРЧЕСКОЕ ЗАДАНИЕ В РАМКАХ СПЕЦКУРСА «НЕСТАНДАРТНЫЕ
ЗАДАЧИ В КУРСЕ АЛГЕБРЫ И НАЧАЛА АНАЛИЗА»)
Найти Sф. , ограниченной осями координат и лежащую в
квадрате, у которого пересечение диагоналей находится в
начале системе координат, стороны квадрата параллельны
осям координат и равны по 12; при этом координаты
точек, составляющих фигуру, удовлетворяют
следующему условию
y≤16/x
y≥x
; (*)
и не удовлетворяют условию: x² + y² + 4 < 4x + 4y. (**)
30.
Решение:Преобразуем x² + y² + 4 = 4x + 4y в
уравнение окружности.
Для этого перенесем 4x + 4y в левую
часть, а также прибавим к обеим частям
уравнения 4 (четыре);
Получаем (x – 2)² + (y - 2)² = 2² ;
где радиус окружности равен 2,
а центр окружности находится в точке
(2;2).
31.
Построим фигуру с учетом (*) и (**),построение не вызывает сложностей.
Ответом этой системы является красная и
оранжевая области.
Теперь изобразим на координатной
плоскости квадрат со стороной 12,
заметим что координаты его вершин
будут удовлетворять точки (6;6), (-6;6), (6;-6) и (6;-6).
Также изображаем круг с центром (2;2) и
R=2.
32.
Площадьфигуры
выделена
красным
33.
Очевидно, что сегменты DD'D" и ВВ'В"имеют равные площади (в силу
нечетности функций у=16/x и равенства
отрезков). То есть можно заменить ВВ'В"
на DD'D".
Далее задача упрощается. Найдем
площадь треугольника ОРВ по формуле
S = (½)·ОР ·РВ; S = (½)·36; S = 18 (кв. ед.).
34.
Нас интересует площадь, закрашеннаякрасным. Итак, Sф =SОРВ– Sполукруга;
Sполукруга = (πR²)/2 = 2π (кв. ед.).
Откуда Sф = 18 - 2π (кв. ед.).
Ответ: Sф = 18 - 2π (кв. ед.).
Ответ : Sф 18 2 (кв.ед.)
35. Задание № 8 (автор ученик 11 б класса морозкин илья, творческое задание в рамках спецкурса «Нестандартные задачи в курсе
ЗАДАНИЕ № 8 (АВТОР УЧЕНИК 11 Б КЛАССА МОРОЗКИН ИЛЬЯ,ТВОРЧЕСКОЕ ЗАДАНИЕ В РАМКАХ СПЕЦКУРСА «НЕСТАНДАРТНЫЕ
ЗАДАЧИ В КУРСЕ АЛГЕБРЫ И НАЧАЛА АНАЛИЗА»)
Решить систему:
log sin y 2 1 cos 2 y 2 cos y
5
3
4
2
4
x
107
x
149
x
12
x
234
x
30
cos( y ) x
2
y 0;2
36.
Решение:1.Упростим систему.
log sin y 2 1
4 x 5 12 x 4 107 x 3 234 x 2 149 x 30 0
sin y x
y 0;2
37.
2.Теперь необходимо упростить второе неравенство.Для этого разложим многочлен на множители,
воспользуемся теоремой Безу.
4 x 5 12 x 4 107 x 3 234 x 2 149 x 30 0
1
x 5; x ; x 1; x 6
2
1
x 5 x x 1 x 6 0
2
38.
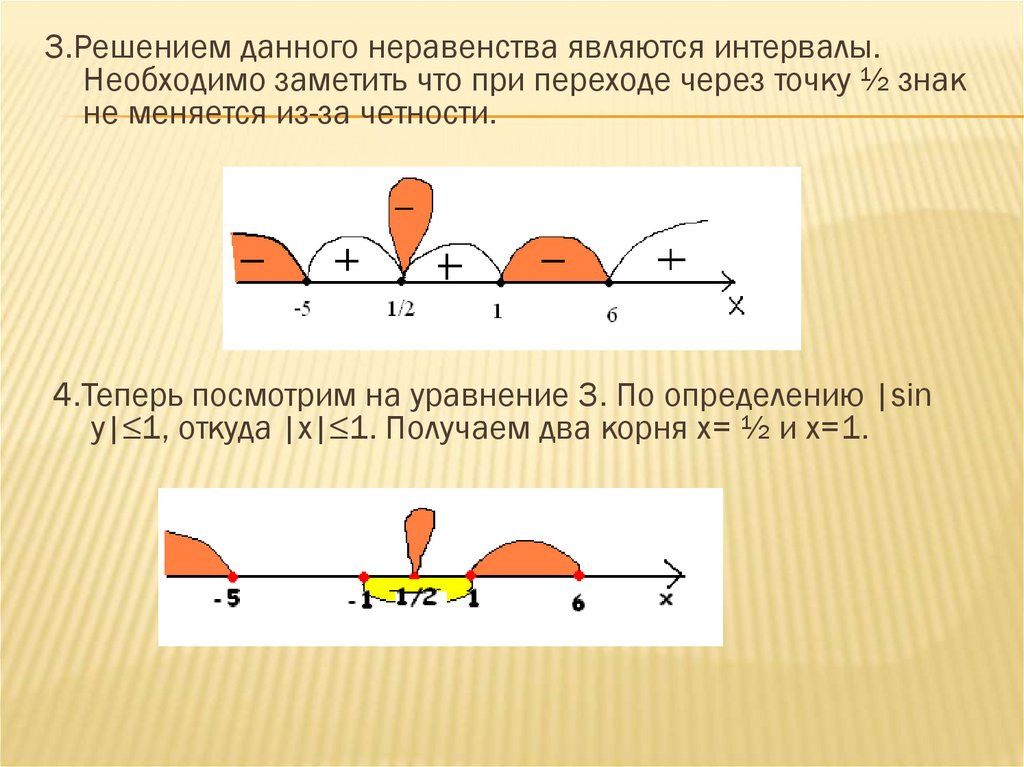
3.Решением данного неравенства являются интервалы.Необходимо заметить что при переходе через точку ½ знак
не меняется из-за четности.
4.Теперь посмотрим на уравнение 3. По определению |sin
y|≤1, откуда |x|≤1. Получаем два корня х= ½ и х=1.
39.
5. Решим неравенство 1. В основаниилогарифма стоит тригонометрическая
функция. 0<sin y<1, так как |sin y|≤1 и sin
y>0, так как стоит в основании логарифма.
При освобождении от логарифма знак
будет меняться на противоположный.
Откуда х≤ ½, то есть х = ½ .
40.
6.Решаем уравнение 3. sin y = ½. Решениемданного уравнения является совокупность.
y
2
k
,
k
Z
6
5
y
2 k , k Z
6
y 0;2, делаем
7.Существует условие
выборку корней.
]k 0; y
6
0;2
5
5
y
0;2
2
6
6
41.
Необходимо сделать проверку системы.Для нее является решением :
х = ½ и у = π/6.
1
Ответ : ;
2 6








































 mathematics
mathematics








