Перевірка статистичних гіпотез. Лекція 13

1. Лекція 13. Перевірка статистичних гіпотез

13.1. Загальні поняття.
13.2. Перевірка гіпотези щодо рівності дисперсій
двох нормально розподілених генеральних
сукупностей.
13.3. Перевірка гіпотези щодо рівності двох
середніх нормальних генеральних сукупностей.
13.4. Перевірка гіпотези щодо рівності вибіркової
середньої математичному сподіванню.
13.5. Критерій згоди відносно частоти.
13.6. Критерії згоди щодо закону розподілу.

2. Види статистичних гіпотез

Статистичною гіпотезою є припущення відносно
параметрів або закону розподілу випадкової
величини. Вихідне твердження про відсутність
істотної відмінності між емпіричною та теоретичною
характеристиками називається основною, або
нульовою гіпотезою H 0 : * . Саме вона і
підлягає перевірці.
Гіпотеза, що розглядає наявність відмінності будьякого знаку, називається конкуруючою, або
альтернативною. Альтернативна гіпотеза може
мати різний зміст в залежності від задачі, що
розглядається. Наприклад, H 1 : * .

3. Висновки щодо основної гіпотези

Наслідком перевірки гіпотези можуть бути
правильні висновки двох типів:
основну гіпотезу нема підстав відхилити, і ця
гіпотеза дійсно є правильною;
основна гіпотеза відхиляється, і вона дійсно
хибна.

4. Статистичні помилки

При перевірці статистичної гіпотези можна
припустити помилку. Ці помилки бувають двох типів.
Помилка першого роду полягає в тому, що
правильна нульова гіпотеза помилково буде
відхилена («хибна тривога»). Ймовірність помилки
першого роду називають рівнем значущості . При
статистичних дослідженнях найбільш поширеними є
рівні значущості 0,05 та 0,01.
Помилка другого роду полягає в тому, що хибна
нульова гіпотеза буде прийнята («небезпека вчасно
не буде поміченою»). Ймовірність помилки другого
роду позначають через .
Оскільки помилки другого роду мають більш важкі
наслідки, то в тому разі, коли виникають сумління,
краще відхилити правильну нульову гіпотезу, ніж
прийняти хибну.

5. Статистичний критерій

Статистичний критерій - це випадкова величина,
що застосовується для перевірки статистичної
гіпотези.
Побудова статистичного критерію передбачає вибір
певною функцією від результатів спостережень
(емпіричних значень ознаки), яка визначає міру
відмінності між емпіричними значеннями та
гіпотетичними.
Статистичні критерії поділяються на параметричні і
непараметричні. До параметричних належать
критерії, застосування яких передбачає обчислення
параметрів розподілу ймовірностей ознаки. Це
критерій Стьюдента, критерій Пірсона, критерій
Фішера. При застосуванні непараметричних
критеріїв обчислюють відповідні частоти або ранги
(критерій Колмогоров, критерій Вілкоксона тощо).

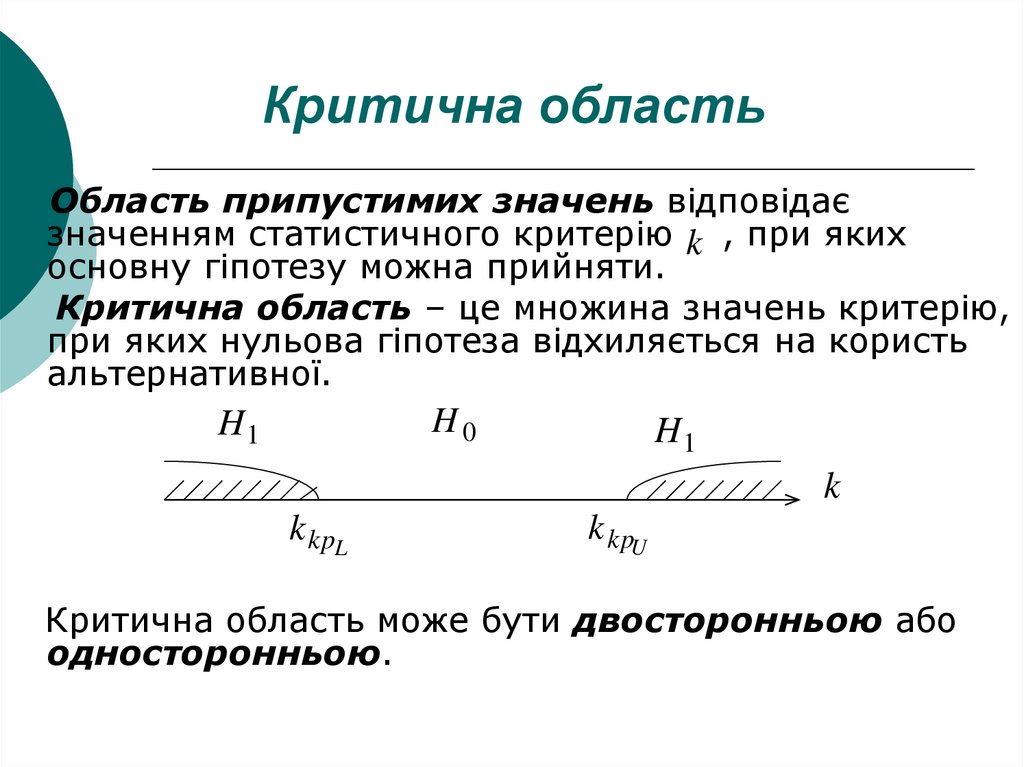
6. Критична область

Область припустимих значень відповідає
значенням статистичного критерію k , при яких
основну гіпотезу можна прийняти.
Критична область – це множина значень критерію,
при яких нульова гіпотеза відхиляється на користь
альтернативної.
H0
H1
H1
k
k kpL
k kpU
Критична область може бути двосторонньою або
односторонньою.

7. Критичні точки

Критичними точками k kpL та k kpU називають
точки, що відділяють критичну область від області
припустимих значень критерію. Якщо k åì . k kpU
або k åì k kp , то гіпотеза H 0 відхиляється.
L
Рівень значущості статистичного критерію
дорівнює ймовірності того, що при правильній
нульовій гіпотезі значення статистичного критерію
належатиме критичній області, що призведе до
необхідності відхилити правильну нульову гіпотезу.
Величина 1 є потужністю критерію, яка
визначає ймовірність попадання значення
статистичного критерію до критичної області за
умови, що альтернативна гіпотеза є справедливою.

8. Перевірка гіпотези щодо рівності дисперсій двох сукупностей

Для нормально розподілених випадкових величин X
та Y утворені дві незалежні вибіркові сукупності
обсягами n і m , для кожної з яких відомі виправлені
дисперсії S X2 і SY2 . Необхідно при заданому рівні
значущості перевірити гіпотезу H 0 : D( X ) D(Y ).
Перевірка здійснюється за критерієм Фішера:
F
S б2
.
Цю величину порівнюють з величиною F ( k1 ; k 2 ), що
визначається за статистикою Фішера при рівні
значущості та кількості степенів свободи k1 більшої
з дисперсій, а також кількості степенів свободи k 2
меншої з дисперсій.
S м2

9. Перевірка гіпотези щодо рівності двох середніх

Є дві вибіркові сукупності обсягами n і m , що
містять значення випадкових величин X та Y,
дисперсії яких невідомі. Необхідно при заданому
рівні значущості перевірити статистичну гіпотезу
H 0 : M ( X ) M (Y ) . В якості альтернативної вибрано
гіпотезу H1 : M ( X ) M (Y ) . Перевірка гіпотези H 0
здійснюється за критерієм Стьюдента:
Tåìï .
x y
mn (m n 2)
m n
(n 1) S X2 (m 1) SY2
з кількістю ступенів свободи k n m 2

10. Критерії згоди щодо закону розподілу

Основна гіпотеза при перевірці припущення щодо
закону розподілу у генеральній сукупності полягає
у тому, що розбіжність між емпіричними частотами
і частотами, що обчислені відповідно до певного
закону розподілу, вважається статистично не
значущою. Для її перевірки застосовується
критерій Пірсона:
2
s
2
i 1
mi mˆ i
mˆ i
,
де s – кількість інтервалів за згрупованим рядом.
Кількість ступенів свободи становить k s r 1 ,
де r – кількість параметрів теоретичного закону