Similar presentations:
Одномерная оптимизация. Метод деления интервала пополам
1. 2.2.5. Метод деления интервала пополам
Метод относится к последовательным стратегиям ипозволяет исключить из дальнейшего рассмотрения на
каждой итерации в точности половину текущего
интервала.
Задается начальный интервал неопределенности [a, b]
и требуемая точность поиска .
Реализация метода основана на выборе трех пробных
точек, равномерно распределенных на текущем
интервале ( делящем его на четыре равные части).
2.
Пусть l b a длина интервала [a, b].Разделим интервал [a, b] точками x1 , xc и x2
четыре равные части
на
l
a b
l
x1 a ; xc
; x2 b .
4
2
4
Вычисляются значения целевой функции f ( x1 ), f ( xc ), f ( x2 ).
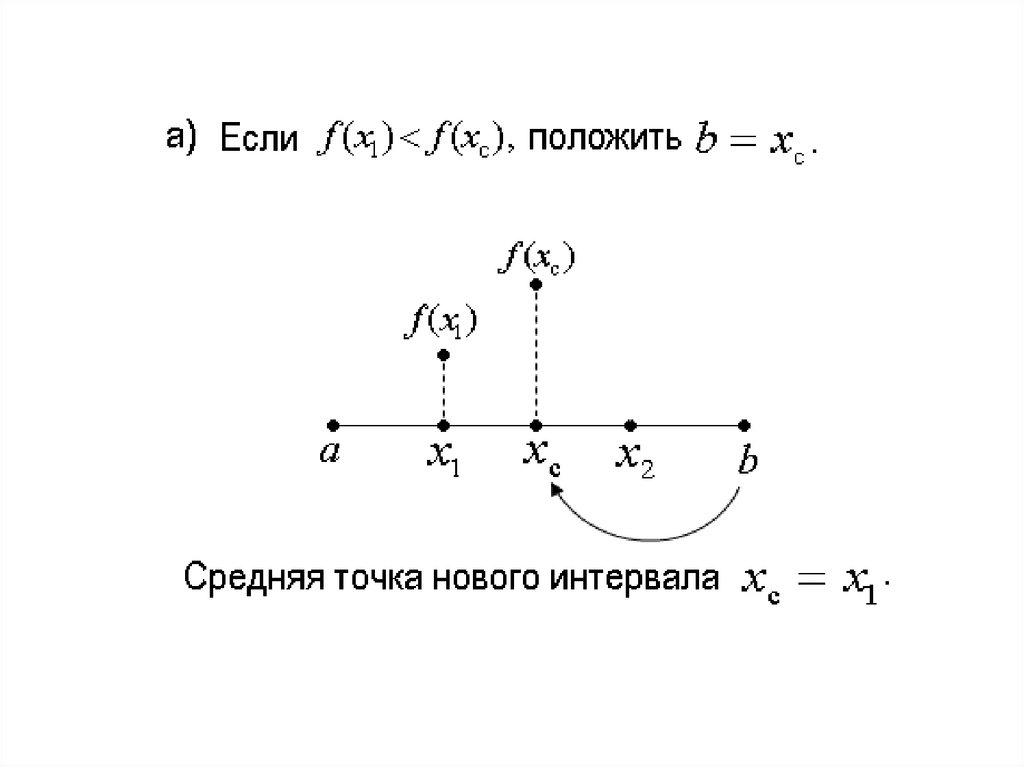
Сравниваются полученные значения и находится новый
интервал неопределенности следующим образом:
3.
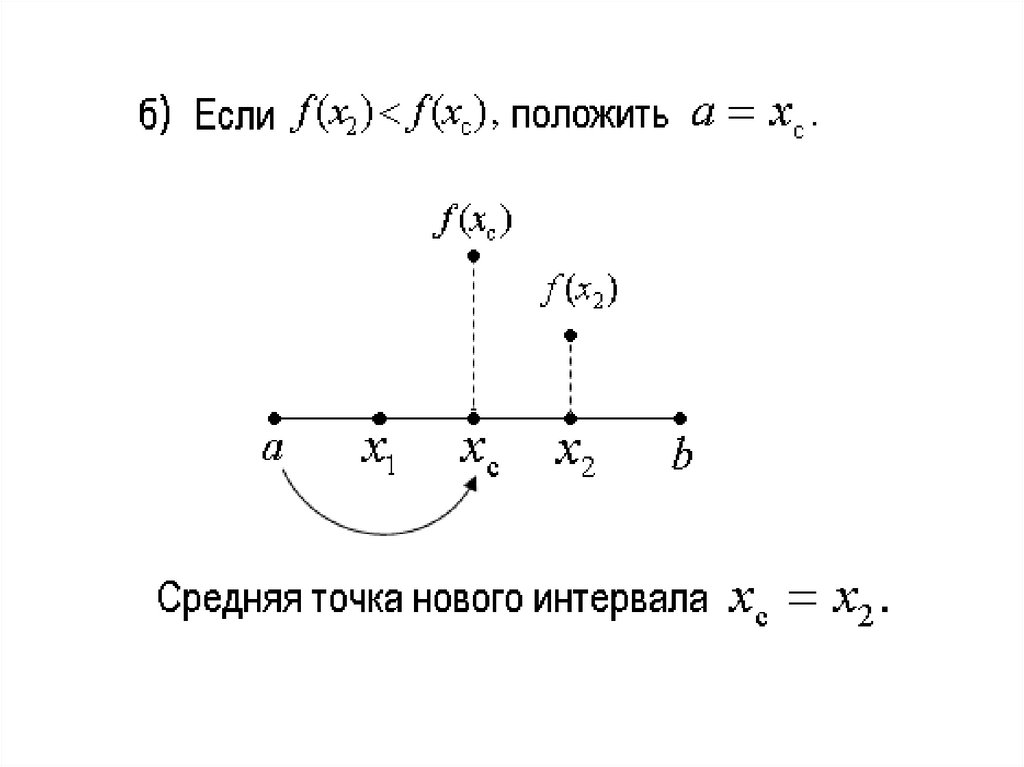
4.
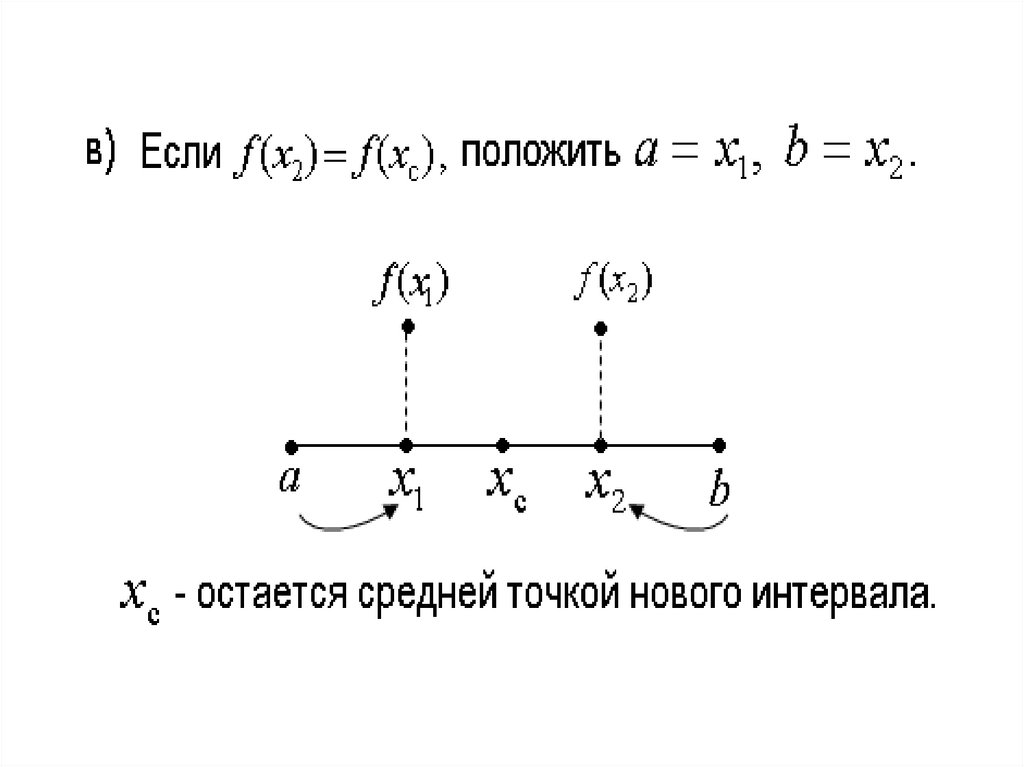
5.
6.
Затем снова вычисляются координаты x1 и x2и продолжают поиск до выполнения условия
b a .
За минимальное значение принимают x xc .
*
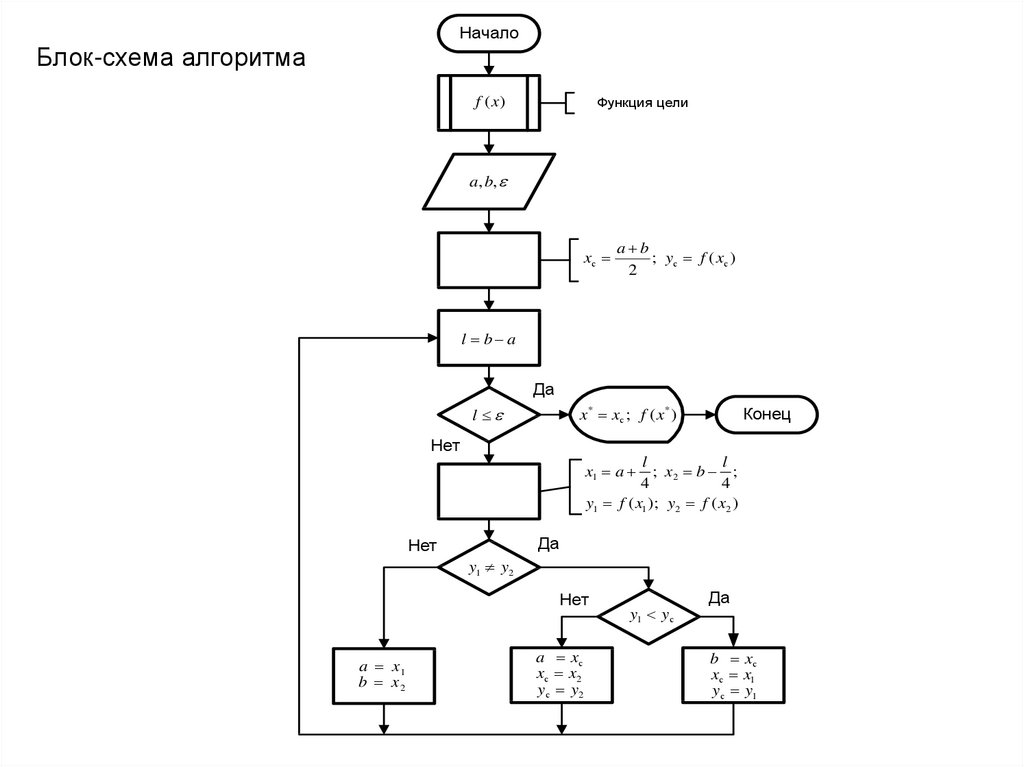
7.
НачалоБлок-схема алгоритма
Функция цели
f (x)
a,b,
xс
a b
; yс f ( xс )
2
l b a
Да
l
x* xс ; f ( x* )
Конец
Нет
l
l
; x2 b ;
4
4
y1 f ( x1 ); y2 f ( x2 )
x1 a
Да
Нет
y1 y2
Нет
a x1
b x2
a xс
xс x2
yс y 2
y1 yс
Да
b xс
xс x1
yс y1
8. 2.2.6. Метод золотого сечения
Метод относится к последовательным стратегиям.Задается начальный интервал неопределенности [a, b]
и требуемая точность поиска .
В качестве точек вычисления целевой функции
выбираются точки золотого сечения. Тогда с учетом
свойств золотого сечения на каждой итерации, кроме
первой, требуется только одно новое вычисление
целевой функции.
9.
Рассмотрим способ размещения точек золотогосечения на интервале [a, b].
Пусть длина интервала равна l , а точка делит его на
две части l1 и l 2 (l1 l2 , l l1 l2 ).
10.
Термин золотое сечение ввел Леонардо да Винчи.Точка называется золотым сечением отрезка l ,
если имеет место соотношение
l1
l2
.
l
l1
Отсюда
l12 l2 l ,
l l2 (l1 l2 ),
2
1
l l2 l1 l 0,
2
2
2
1
11.
2l2 l2
1 0,
l1 l1
l2 1 5 1 2,236
.
l1
2
2
Так как нас интересует только положительное
решение, то
l2 1 2,236
0,618.
l1
2
12.
Из этого соотношения имеемl1 l2
0,618 ;
l l1
l1 0,618 l ;
l2 0,618 l1 ( 0,618 ) l 0,382 l.
2
13.
Поскольку заранее неизвестно, в какойпоследовательности ( l 1 l2 или l1 l2 ) делить
интервал неопределенности, то рассматривают
внутренние точки, соответствующие двум этим
способам деления
14.
Точки деления x1 изначений
x2
с учетом полученных
x1 a 0,382(b a),
x2 a 0,618(b a).
Новый уменьшенный интервал неопределенности
выбирается следующим образом.
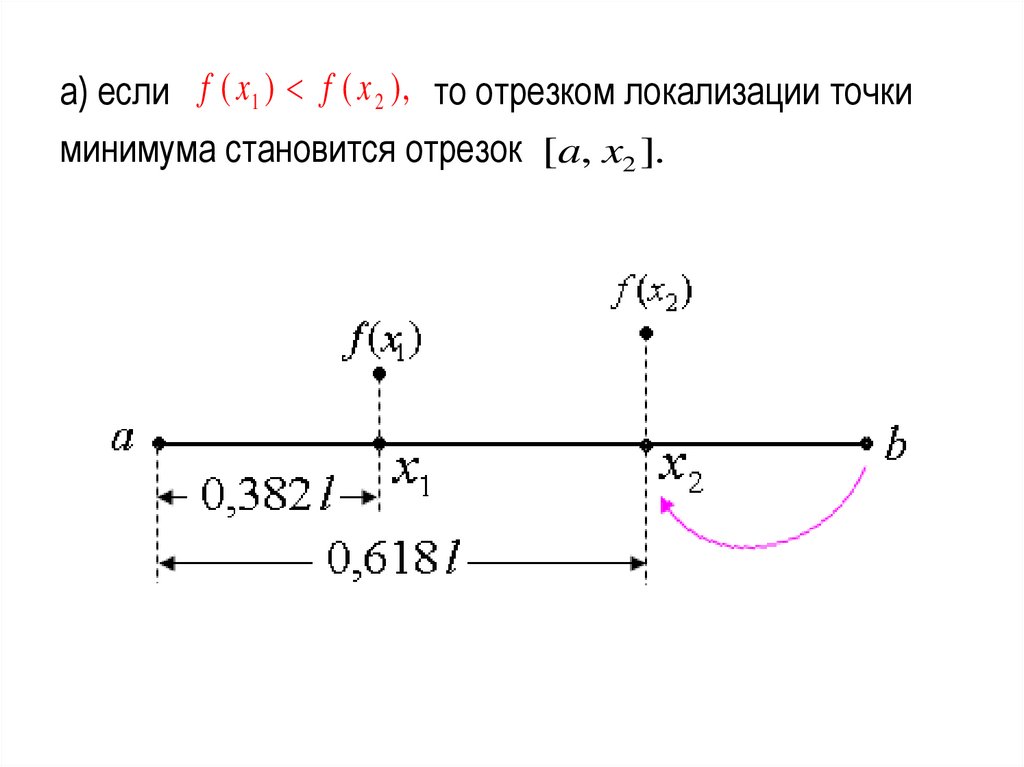
15.
а) если f ( x 1 ) f ( x 2 ), то отрезком локализации точкиминимума становится отрезок [a, x2 ].
16.
Определим положение точки x1Вычислим отношение
на интервале
[a, x2 ].
0,382 l
k
0,618.
0,618 l
Следовательно точка x1 является второй точкой
золотого сечения отрезка [a, x2 ].
Положим b x2
x x
1
2
f ( x2 ) f ( x1 )
x a 0,382 (b a )
1
Вычислить f ( x1 )
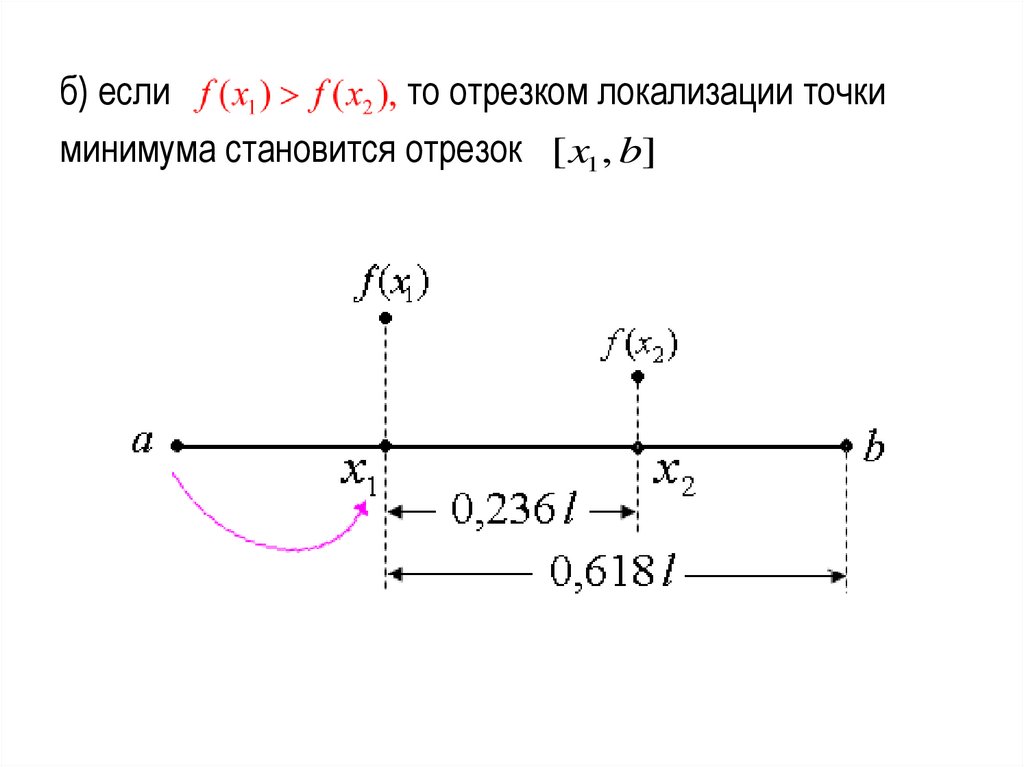
17.
б) еслито отрезком локализации точки
минимума становится отрезок [ x1 , b]
18.
Определим положение точки x2 на интервале [ x1, b].Вычислим отношение
k
0,236 l
0,382.
0,618 l
Следовательно точка x2 первая точка
золотого сечения отрезка [ x1, b].
Положим
a x
1
x x
1
2
f ( x1 ) f ( x2 )
x a 0,618 (b a )
2
Вычислить f ( x2 )
19.
Процесс оптимизации заканчивается при выполненииусловия b a .
В качестве минимального значения берется середина
последнего интервала
a b
x
.
2
*
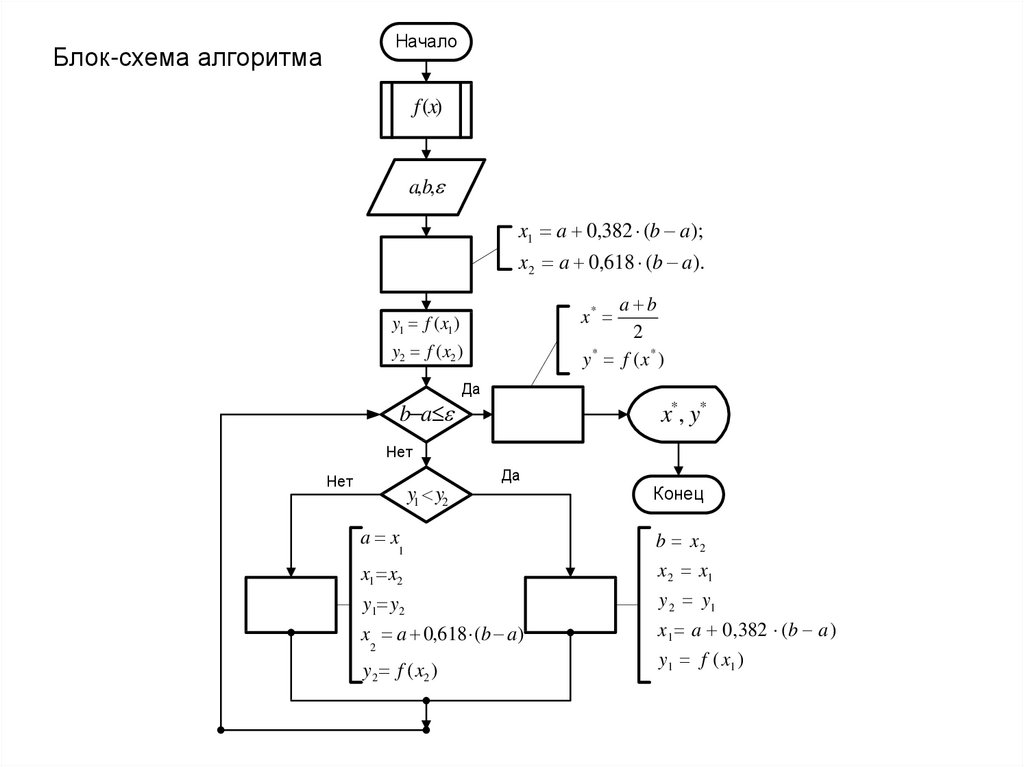
20.
НачалоБлок-схема алгоритма
f (x)
a,b,
x1 a 0,382 (b a );
x 2 a 0,618 (b a ).
a b
2
*
y f ( x* )
x*
y1 f ( x1 )
y2 f ( x2 )
b a
Да
x*, y*
Нет
Нет
y1 y2
Да
Конец
a x
b x2
x1 x2
x 2 x1
1
y1 y 2
x a 0,618 (b a)
2
y 2 f ( x2 )
y 2 y1
x 1 a 0 ,382 ( b a )
y1 f ( x1 )
21.
При n 2 эффективность метода золотого сечениявыше, чем у метода дихотомии, так как при каждом
последующем вычислении целевой функции интервал
1
неопределенности уменьшается в
раза.
0,618
b a
За n итераций длина интервала будет равна n .
Точность на n шаге вычислений можно оценить
b a
неравенством n .
Отсюда следует, что для достижения требуемой точности
требуется
n
итераций.
ln[( b a) / ]
ln
22. 2.2.7. Метод Фибоначчи
Метод Фибоначчи относится к последовательнымстратегиям и обеспечивает максимальное
сокращение интервала неопределенности при
заданном количестве вычислений целевой функции.
Алгоритм поиска по методу Фибоначчи
определяется тем же правилом симметрии, что и
алгоритм по методу золотого сечения: на первой
итерации выбираются две точки, расположенные
симметрично внутри интервала неопределенности ;
на каждой последующей итерации точка очередного
вычисления выбирается симметрично оставшейся
точки. Разница заключается в выборе точек.
23.
Для простоты изложения алгоритмарассмотрим интервал неопределенности
[ x1 , x3 ] [a, b]. Обозначим через - длину L
1
интервала [ x1 , x3 ].
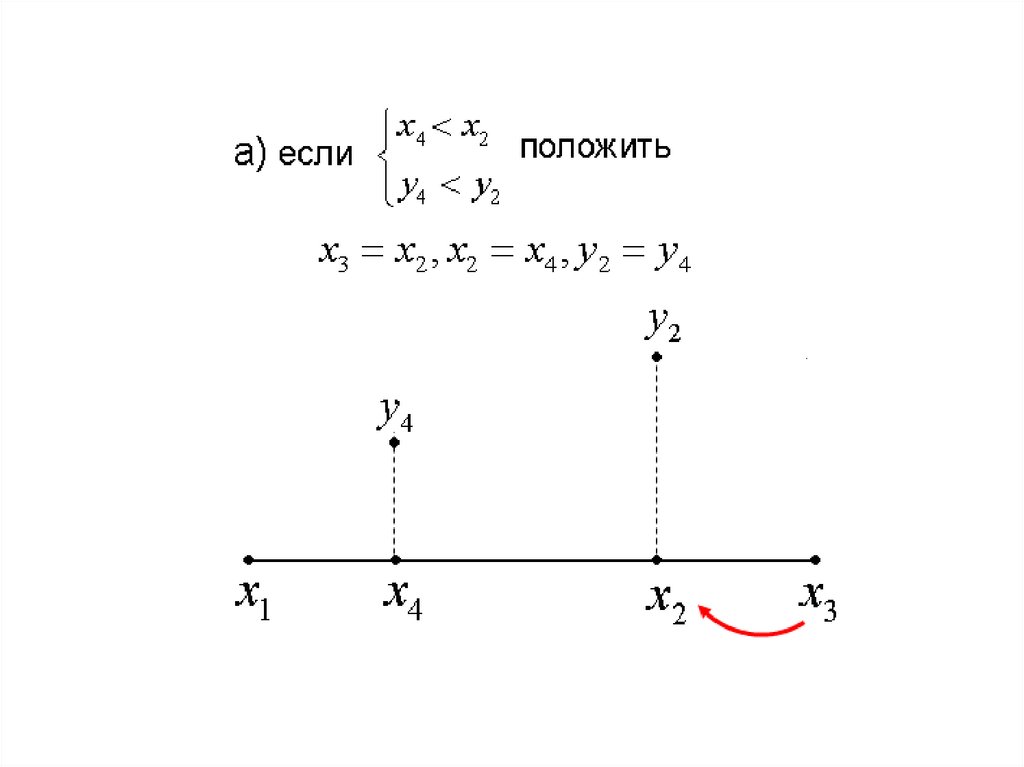
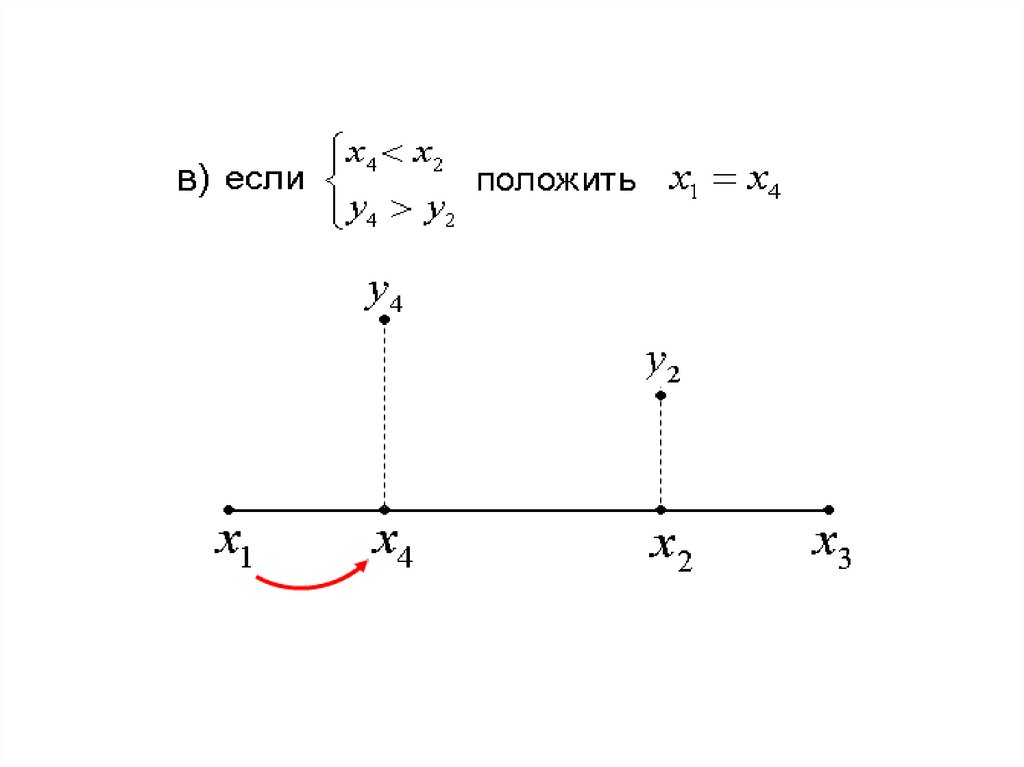
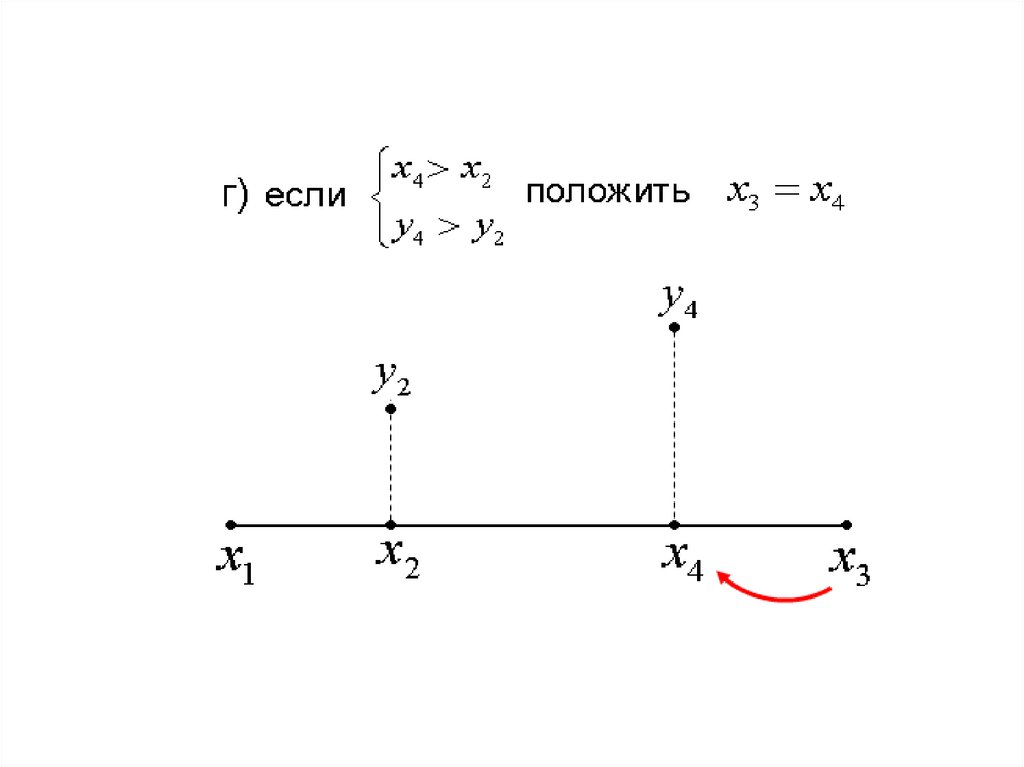
24.
25.
Предположим, что на расстоянии L2 отодного из концов интервала неопределенности
[ x1 , x3 ] помещена точка x2 . Вторая точка x4
располагается симметрично относительно
середины отрезка
x 4 x ( x2 x )
2 x x2
x1 x3
x x
x2 1 3 x1 x 2 x3 .
2
2
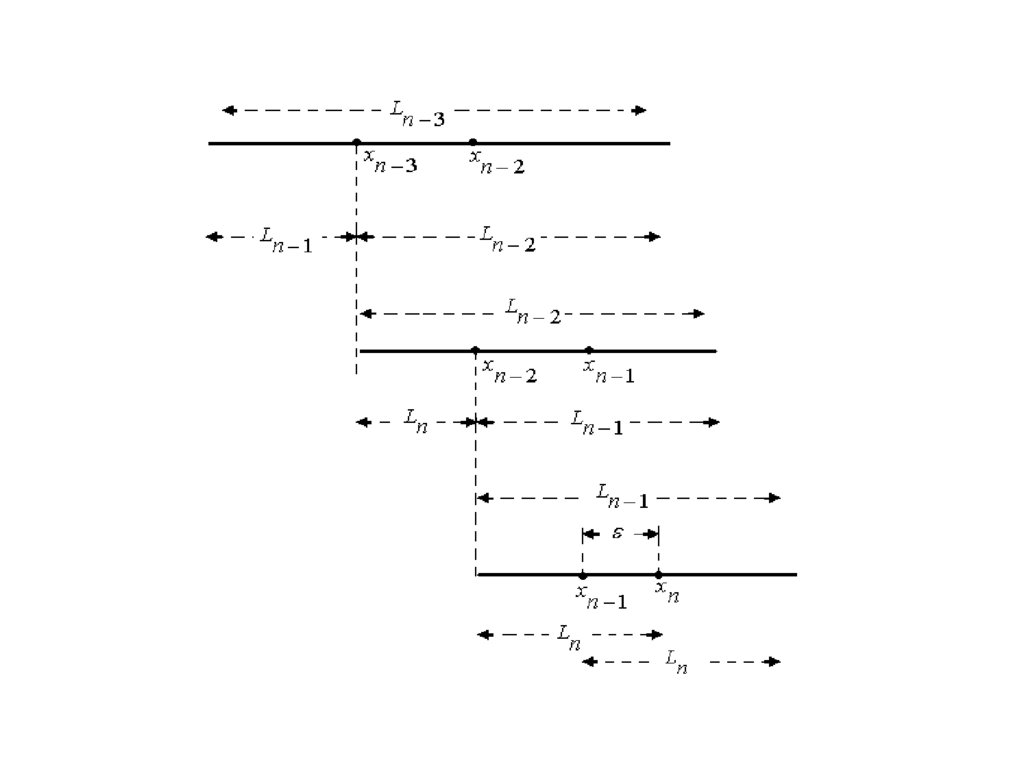
26.
Определим величину L2 . Для этогорассмотрим n - ю итерацию.
Для того, чтобы получить наибольшее
уменьшение интервала неопределенности,
расположим точки x n 1 и x n на расстоянии / 2
по обе стороны от середины отрезка Ln 1 (см.
рисунок).
27.
28.
Интервал неопределенности будет иметьдлину Ln , следовательно Ln 1 2Ln .
На предыдущем этапе точки xn 1 и xn 2
должны быть помещены симметрично
внутри интервала Ln 2 . Следовательно
Ln 2 Ln 1 Ln .
Аналогично Ln 3 Ln 2 Ln 1.
29.
Таким образом,L n 1 2 Ln ,
Ln 2 Ln 1 Ln 3Ln ,
Ln 3 Ln 2 Ln 1 5Ln 2 ,
Ln 4 Ln 3 Ln 2 8Ln 3
и так далее.
30.
Общее выражение для произвольного интерваланеопределенности имеет вид
Ln j F j 1 Ln F j 1 , j 1,2, . . . , n 1,
(2.2)
где коэффициенты F j называются числами Фибоначчи
и определяются следующим образом
F0 1, F1 1, Fk Fk 1 Fk 2 ,
k 2, 3, . . .
Последовательность чисел Фибоначчи имеет вид
0 1 2 3 4 5
6
7
8
9
10
11
12
1 1 2 3 5 8 13 21 34 55
89
144
233
31.
Пусть начальный интервал неопределенности имеетдлину L1 b a (a x1 , b x3 ) Через числа Фибоначчи
выражение для определения L1 можно получить из
выражения (2.2), полагая j n 1. L1 Fn Ln Fn 2 .
Из последнего выражения найдем длину
интервала неопределенности на n -й итерации
L1 Fn 2
Ln
.
Fn Fn
Далее, используя выражение (2.2), находим положение
первой точки x2 , которая помещается на расстоянии L2
от одного из концов начального интервала.
32.
При j n 2, получим33.
Используемое значениеиз условия
определяется
b a
.
Fn
После того как найдено положение первой
точки, числа Фибоначчи больше не
используются.
Приведем дальнейшую схему вычисления
интервала неопределенности.
Вычислим y2 f ( x2 ), y4 f ( x4 ).
34.
35.
36.
37.
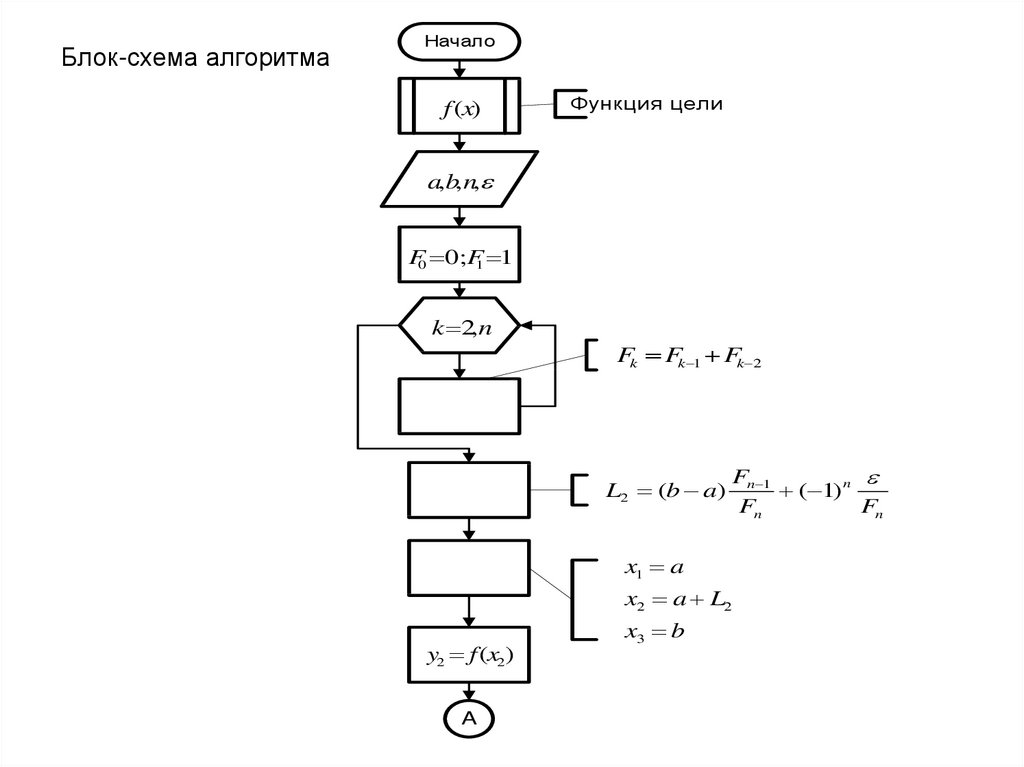
38.
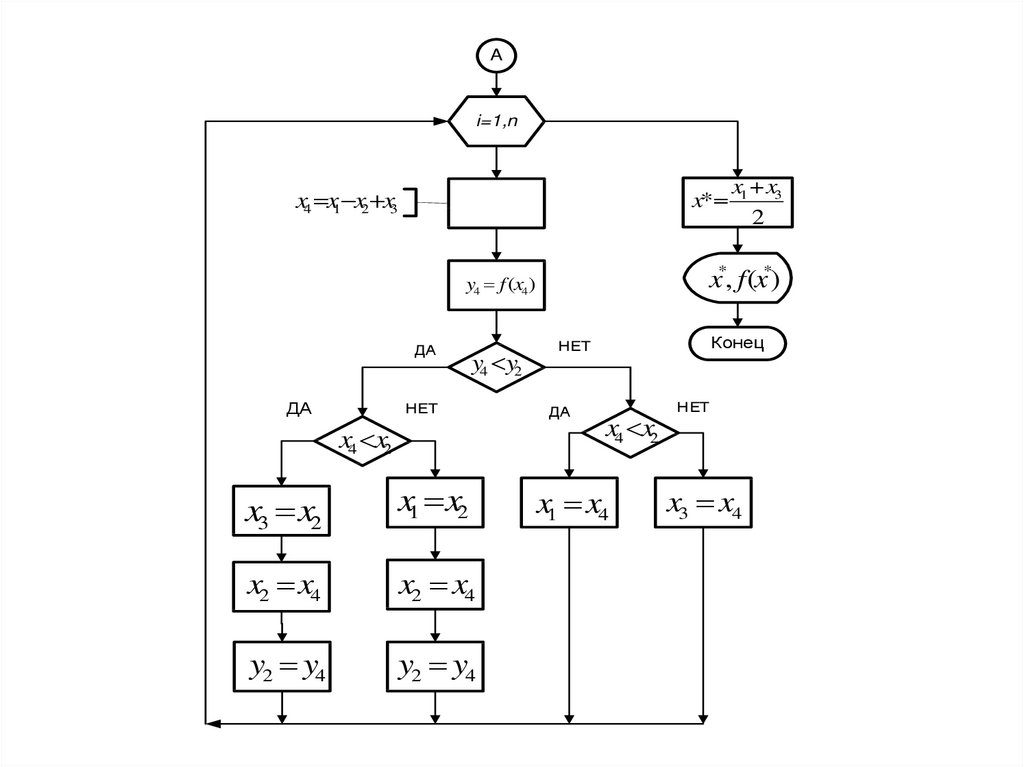
Блок-схема алгоритмаНачало
f (x)
Функция цели
a,b,n,
F0 0;F1 1
k 2,n
Fk Fk 1 Fk 2
L2 (b a)
x1 a
x2 a L2
y2 f (x2)
A
x3 b
Fn 1
( 1) n
Fn
Fn
39.
Ai=1,n
x4 x1 x2 x3
x*
x*, f (x*)
y4 f (x4)
ДА
ДА
y4 y2
НЕТ
x4 x2
x3 x2
x1 x2
x2 x4
x2 x4
y2 y4
y2 y4
x1 x3
2
Конец
НЕТ
ДА
x4 x2
x1 x4
НЕТ
x3 x4
40.
Заметим, что при достаточно большихзначение
n
стремится к 0.618, так что методы Фибоначчи и
золотого сечения становятся асимптотически
эквивалентными
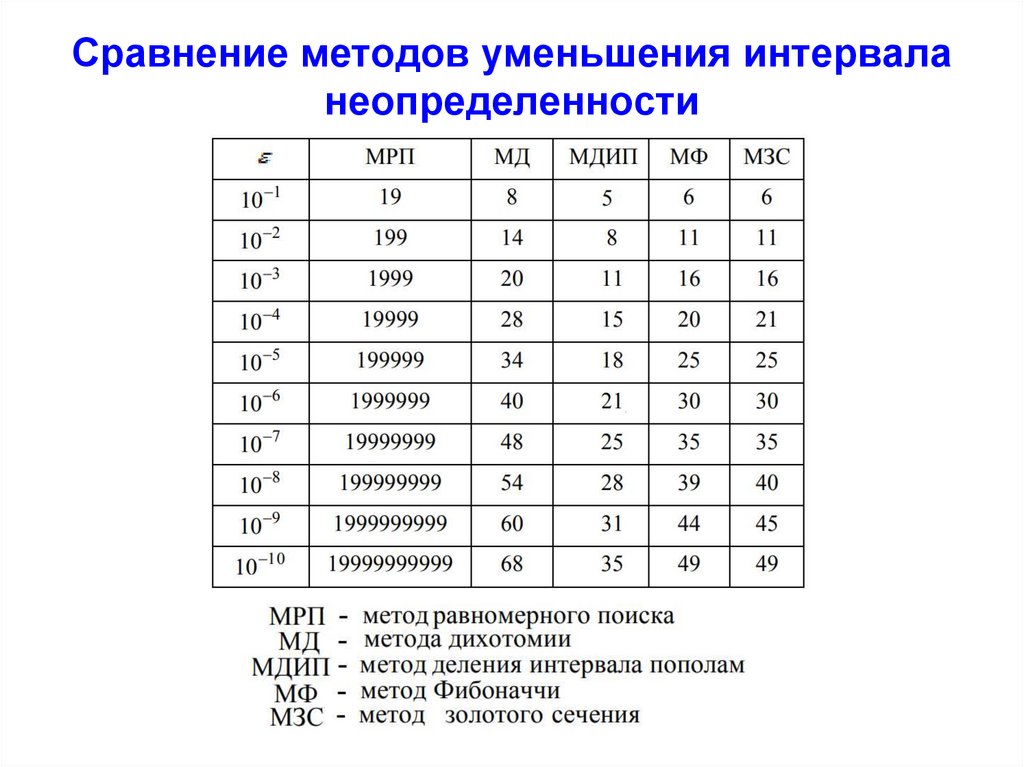
41. Сравнение методов уменьшения интервала неопределенности
42. 2.2.8. Метод квадратичной аппроксимации
Основная идея метода связана с возможностьюаппроксимации гладкой функции полиномом и
последующего использования аппроксимирующего
полинома для оценивания координат точки минимума.
Пусть известны значения целевой функции f (x) в
трех различных точках x1 , x 2 , x3 , равные
соответственно y1 f ( x1 ), y2 f ( x2 ), y3 f ( x3 ).
Запишем интерполяционный многочлен в форме
Лагранжа
( x) a0 a1 ( x x1 ) a2 ( x x1 )( x x2 ).
(2.2)
43.
Вычислим значения(x )
в каждой из трех точек
x1 , x 2 , x3 .
При
x x1 a0 y1 ,
при
x x 2 y2 a0 a1 ( x2 x1 ),
y 2 y1
a1
,
x2 x1
при
(2.3)
(2.4)
x x3 ,
( x3 ) a0 a1 ( x3 x1 ) a2 ( x3 x1 )( x3 x2 )
44.
Разрешая последнее уравнение относительно a2 ,получим
1 y3 y1
a2
a1 .
x 3 x2 x3 x1
(2.5)
Из уравнения (2.2)
a1 a2 ( x x2 ) a2 ( x x1 ) 0.
x
45.
находим точкуx1 x2
a1
x
.
2
2a 2
(2.6)
Поскольку аппроксимирующий квадратичный полином
является унимодальной функцией, то коэффициент a2
при старшем члене (x ) будет положителен.
Следовательно, в точке x полином (x )
имеет локальный минимум.
46.
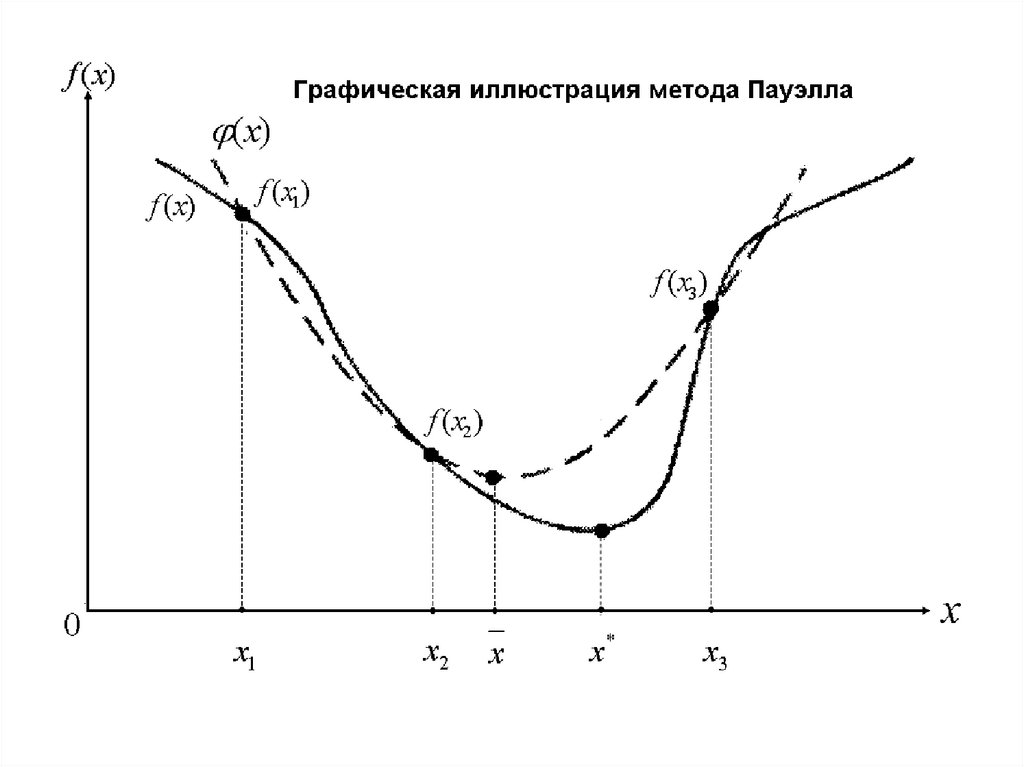
Рассмотрим алгоритм квадратичнойинтерполяции, называемый методом Пауэлла.
Пусть x1 начальная точка, x - величина шага
по оси x и 1, 2 числа, характеризующие точность
поиска.
1. Вычислить точку x2 x1 x.
2. Вычислить значения целевой функции в точках x1 , x2 :
y1 f ( x1 ), y2 f ( x2 ).
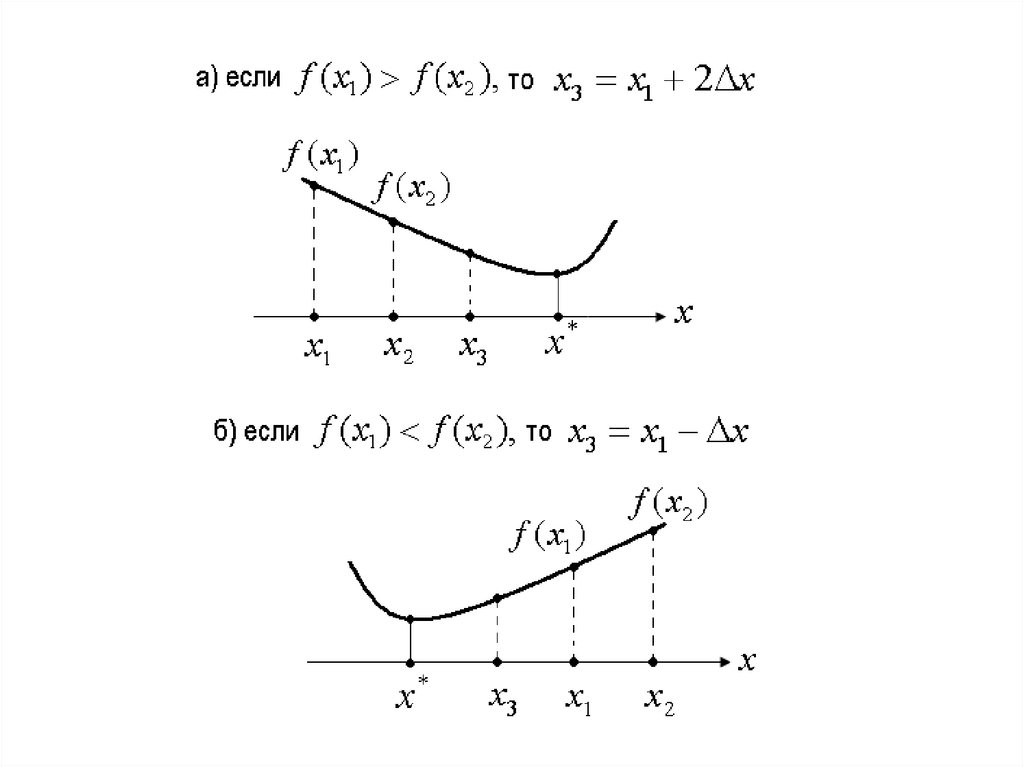
3. Сравнить значения f ( x1), f ( x2 ) и найти точку x3
так, чтобы точки x1 , x 2 , x3 были как можно ближе к
искомой точке минимума.
47.
48.
y 3 f ( x 3 ).4.
Вычислить
5.
Найти F min f ( x 1 )
6.
f ( x 2 ) f ( x 3 ) , x min x i , f ( x i ) F min .
По трем точкам x1 , x2 , x3 вычислить x, используя
формулу (2.6) и величину f (x ).
Если знаменатель в формуле (2.6) на некоторой
итерации обращается в нуль, то результатом
интерполяции будет прямая. В этом случае
рекомендуется обозначить x1 x min и перейти
к пункту 1.
49.
6.Проверить условие окончания процесса вычислений
xmin x
Fmin f ( x)
1 ,
2.
f ( x)
x
Если оба условия выполнены, то поиск закончен и
*
x x. В противном случае выбрать наилучшую
точку ( xmin или x ) и две точки по обе стороны от
нее. Обозначить их в естественном порядке и
перейти к пункту 5.
50.
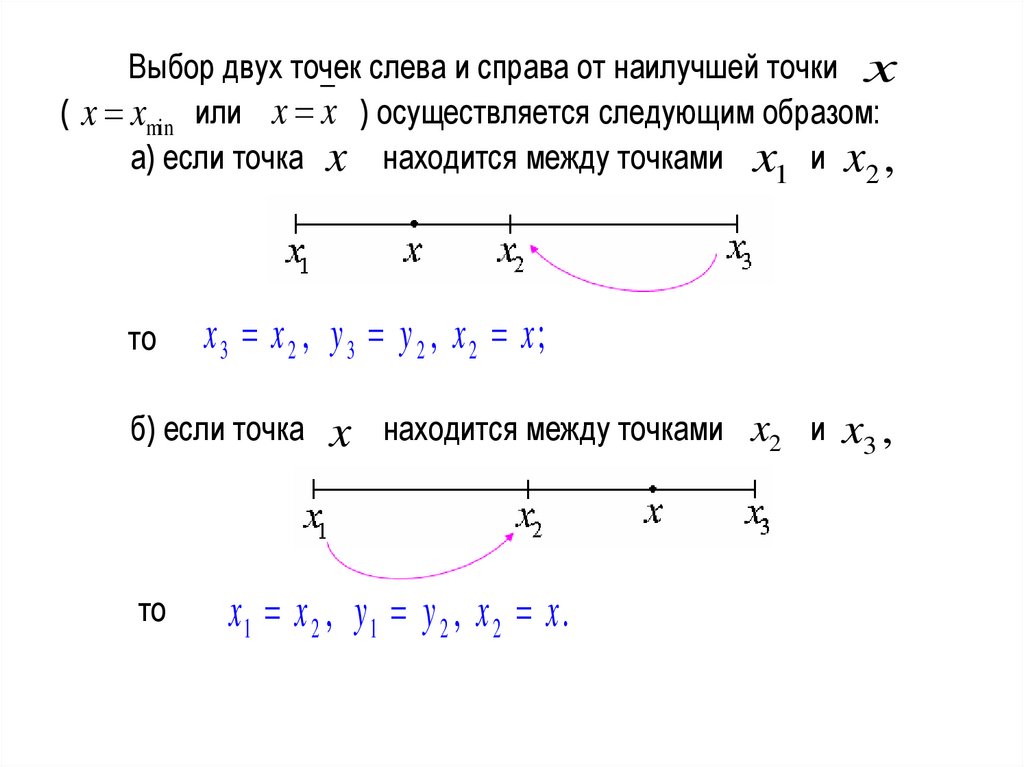
Выбор двух точек слева и справа от наилучшей точки x( x xmin или x x ) осуществляется следующим образом:
а) если точка x находится между точками x1 и x2 ,
то
x3 x2 , y3 y 2 , x2 x;
б) если точка
то
x
находится между точками x2 и
x1 x 2 , y 1 y 2 , x 2 x .
x3 ,
51.
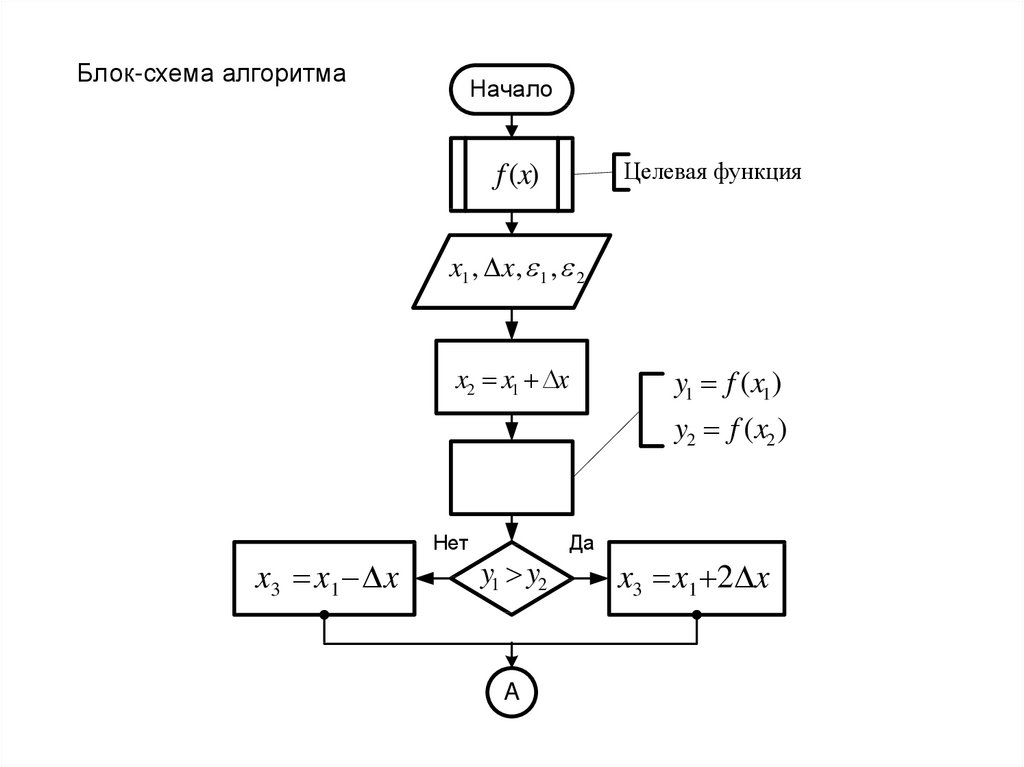
52.
Блок-схема алгоритмаНачало
Целевая функция
f (x)
x1 , x , 1 , 2
x2 x1 x
y1 f (x1)
y2 f (x2 )
Нет
x3 x 1 x
y1 y2
A
Да
x3 x1 2 x
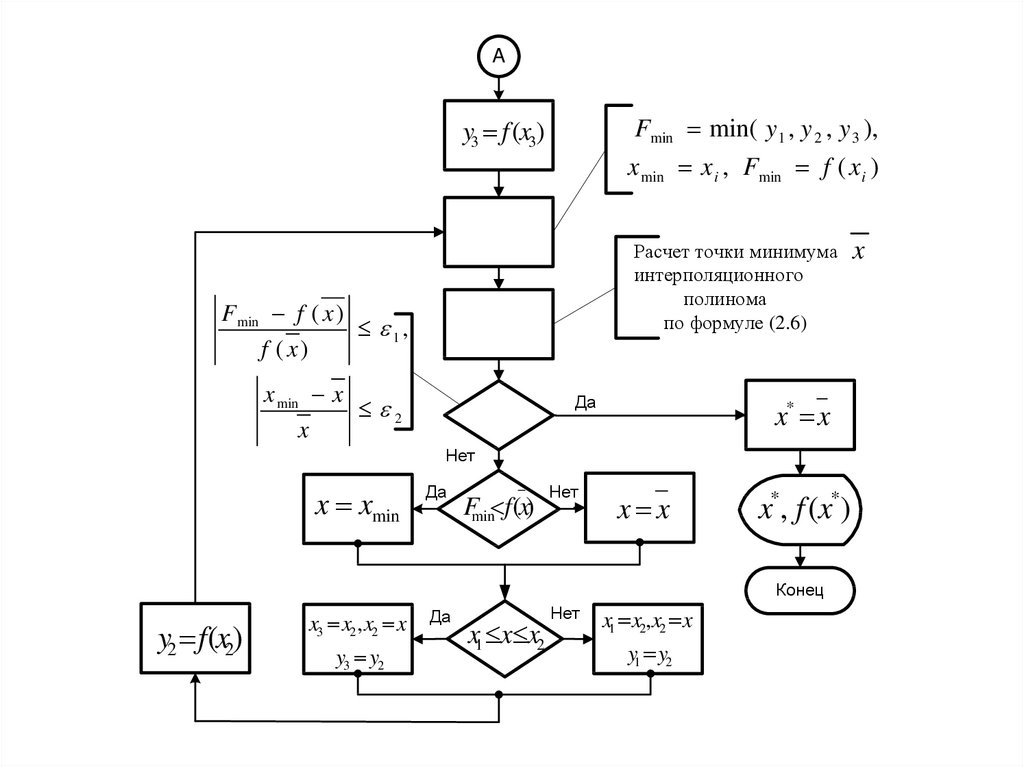
53.
AFmin min( y1 , y 2 , y 3 ),
y3 f (x3)
x min x i , Fmin f ( x i )
Расчет точки минимума
интерполяционного
полинома
по формуле (2.6)
F min f ( x )
1,
f ( x)
x min x
2
x
Да
x* x
Нет
x xmin
Да
Fmin f(x)
Нет
x x
x*, f (x*)
Конец
y2 f (x2)
x3 x2, x2 x
y3 y2
Да
x1 x x2
Нет
x1 x2, x2 x
y1 y2
x
54.
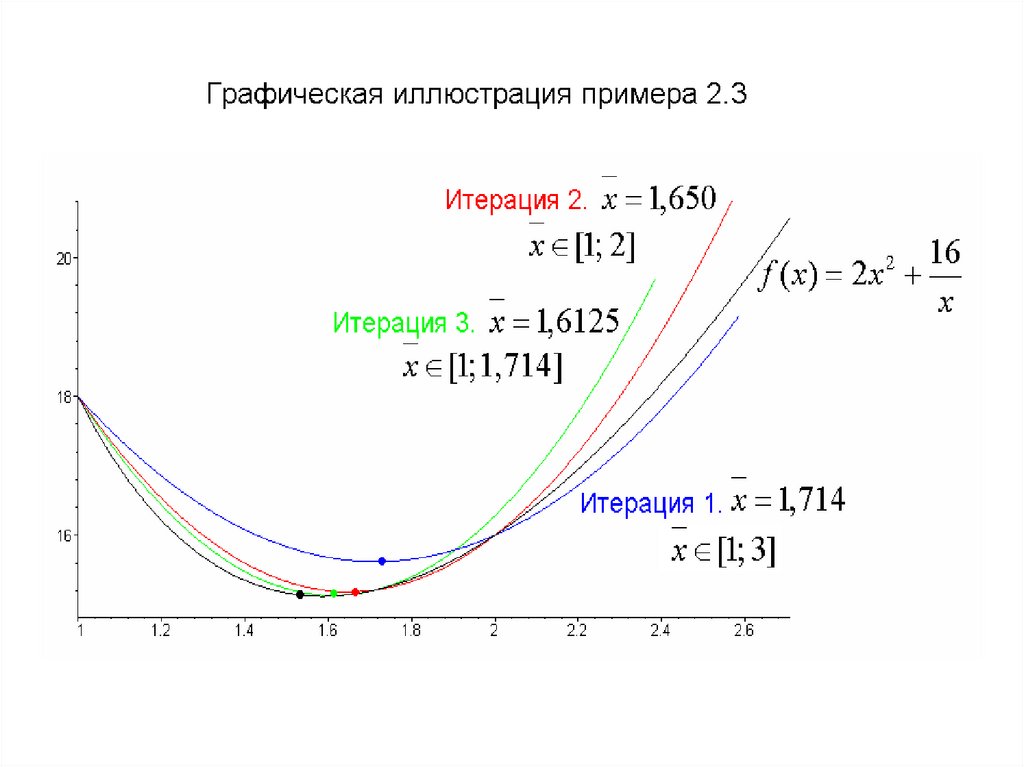
Пример 2.3. Минимизировать функцию16
f x 2 x
x
2
методом Пауэлла с точностью 1 0,003, 2 0,03.
Решение. Зададим начальную точку x1 1 и величину шага
x 1.
Итерация 1. Вычислим x2 x1 x 2 и f ( x1 ) 18, f ( x2 ) 16.
Так как f ( x1 ) f ( x2 ), то положим x3 x1 2 x 1 2 3.
Вычислим f ( x3 ) 23,33.
Найдем Fmin 18; 16; 23,33 16, xmin x2 2.
По формулам (2.4) и (2.5) найдем a1 2, a2 4,665.
По формуле (2.6) вычислим точку интерполяционного полинома
x 1, 714 и величину целевой функции f ( x ) 1 5 , 2 1 .
55.
Проверим условие окончания поискаFmin f ( x) 16 15,21
0,0519 0,003
15,21
f ( x)
(не выполняется),
следовательно продолжаем поиск. Учитывая, что
выбираем x 1,714 как наилучшую точку. Слева от нее x1 1,
а справа x3 2.
Обозначим их в естественном порядке x 1 1; x 2 1, 7 1 4 ; x 3 2 .
Этим точкам соответствуют значения целевой функции
f ( x1 ) 18; f ( x2 ) 15,21; f ( x3 ) 16.
Итерация 2.
Fmin (18; 15,21; 16) 15,21; xmin 1,714.
56.
По формулам (2.4) и (2.5) найдем a1 3,908; a2 6,671.По формуле (2.6) вычислим точку интерполяционного полинома
x 1, 650 и величину целевой функции f ( x ) 1 5 ,1 4 2 .
Проверим условие окончания поиска
Fmin f ( x) 15,21 15,142
0,0045 0,003
15,142
f ( x)
- условие не выполняется.
Выбираем x 1,65 как наилучшую точку. Слева от нее x1 1,
а справа x3 1,714.
Обозначим их в естественном порядке x 1 1; x 2 1, 6 5 ; x 3 1, 7 1 4 .
Этим точкам соответствуют значения целевой функции
f ( x1 ) 18; f ( x2 ) 15,142; f ( x3 ) 15,21.
57.
Итерация 3. Fmin (18; 15,142; 15,21) 15,142; xmin x2 1,65.По формулам (2.4) и (2.5) найдем a1 4,397; a2 7,647.
По формуле (2.6) вычислим точку интерполяционного полинома
x 1,6125 и величину целевой функции f ( x) 15,123.
Проверим условие окончания поиска
Fmin f ( x) 15,142 15,123
0,0013 0,003;
15,123
f ( x)
xmin x 1,65 1,6125
0,023 0,03.
1,6125
x
Следовательно, поиск закончен. Решение
x x 1, 6 1 2 5 ; f ( x ) 1 5 ,1 2 3 .
*
*
58.
Найдем аналитически координату точки минимумаdf ( x)
16
4 x 2 0 x 3 4 x* 3 4 1,5874.
dx
x
Проверим выполнение достаточного условия экстремума
d 2 f ( x)
32
4 3 .
2
dx
x
В точке
d 2 f ( x* )
12 0
x 1, 5874 выполняется условие
2
dx
*
- следовательно целевая функция в данной точке имеет минимум.







































 mathematics
mathematics








