Similar presentations:
Електропровідність халькогенідних склоподібних напівпровідників. (Лекція 6)
1. Лекція 6. Електропровідність халькогенідних склоподібних напівпровідників
2.
Анізотропія електропровідності шаруватих кристалівАнізотропія
електропровідності
шаруватих кристалів
визначається
параметром = / , який температурно активується = A exp( E/kT).
, Ом-1/см-1
, Ом-1/см-1
10–2
10–4
10–4
10
10–6
–6
||
10–8
||a
10–10
10
10–8
||b
–12
2
4
6
а
8
103/T, K–1
10–10
10
10–12
2
3
4
5
б
6
7
103/T, K–1
Рис. 1. Температурні залежності електропровідності кристалів GeS,
вирощених методом Піццарелло (а) та Бріджмена (б).
3.
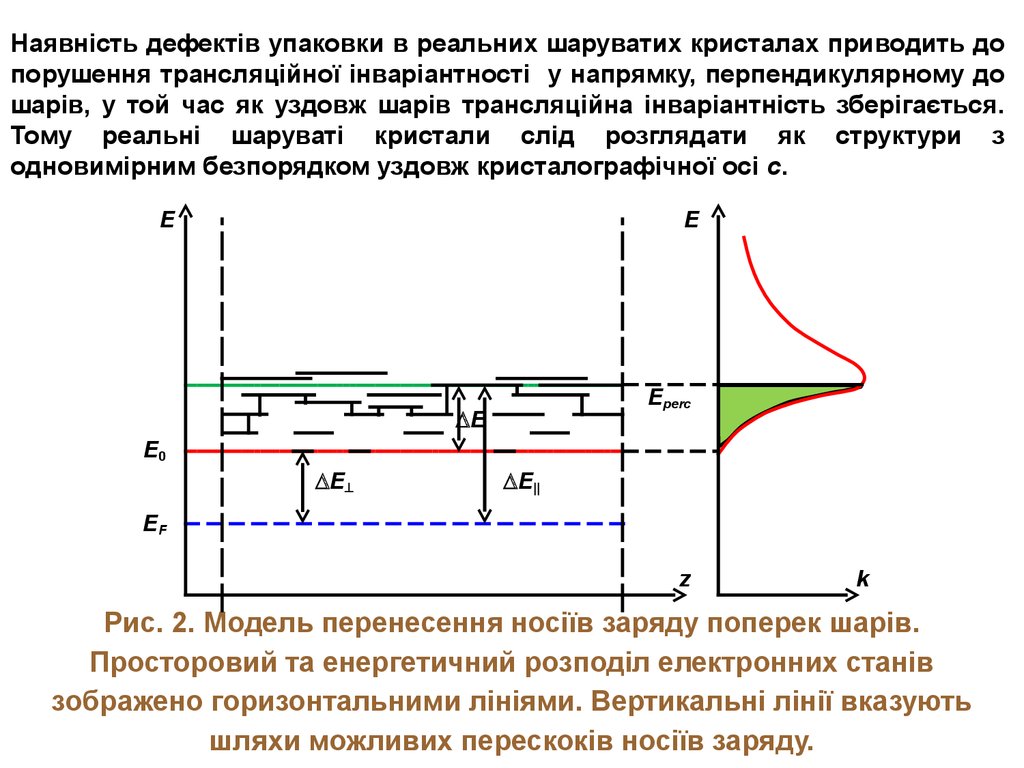
Наявність дефектів упаковки в реальних шаруватих кристалах приводить допорушення трансляційної інваріантності у напрямку, перпендикулярному до
шарів, у той час як уздовж шарів трансляційна інваріантність зберігається.
Тому реальні шаруваті кристали слід розглядати як структури з
одновимірним безпорядком уздовж кристалографічної осі с.
E
E
Eperc
E
E0
E
E||
EF
z
k
Рис. 2. Модель перенесення носіїв заряду поперек шарів.
Просторовий та енергетичний розподіл електронних станів
зображено горизонтальними лініями. Вертикальні лінії вказують
шляхи можливих перескоків носіїв заряду.
4.
Поаналогії
з
аморфними
напівпровідниками,
феноменологічний опис властивостей переносу в
шаруватих кристалах можна здійснити, увівши край
рухливості (Ереrc) для провідності поперек шарів.
Внаслідок розповсюджуваного характеру блохівських
хвильових функцій вздовж шарів, енергія активації
переносу в режимі постійного струму у цьому напрямі
рівна Ea = E0 – Eperc, як у звичайному напівпровіднику, а
поперек шарів ефективна енергія активації Ea = Eperc –
EF. Тоді Eperc – E0 = Е є експериментально визначена
енергія активації переносу у режимі постійного струму
поперек шарів.
5.
а)Е
Е
б)
Е
Ес
ЕА
Ес
Ес
ЕА
ЕF
ЕF
ЕF
Еv
Ев
Еv
Ев
Еv
N(E)
Ес
ЕА
д)
Е
Ес
ЕА
Ex
ЕF
N(E)
N(E)
г)
Е
1.29
0.66 Е2
D
Е3
0.30 Е4
Ев
Еv
N(E)
Е1
0.92 ЕF
ЕF
Ев
Еv
Е
ж)
2.0 Ес
A
EY
в)
C 3
C1
Еv
N(E)
N(E)
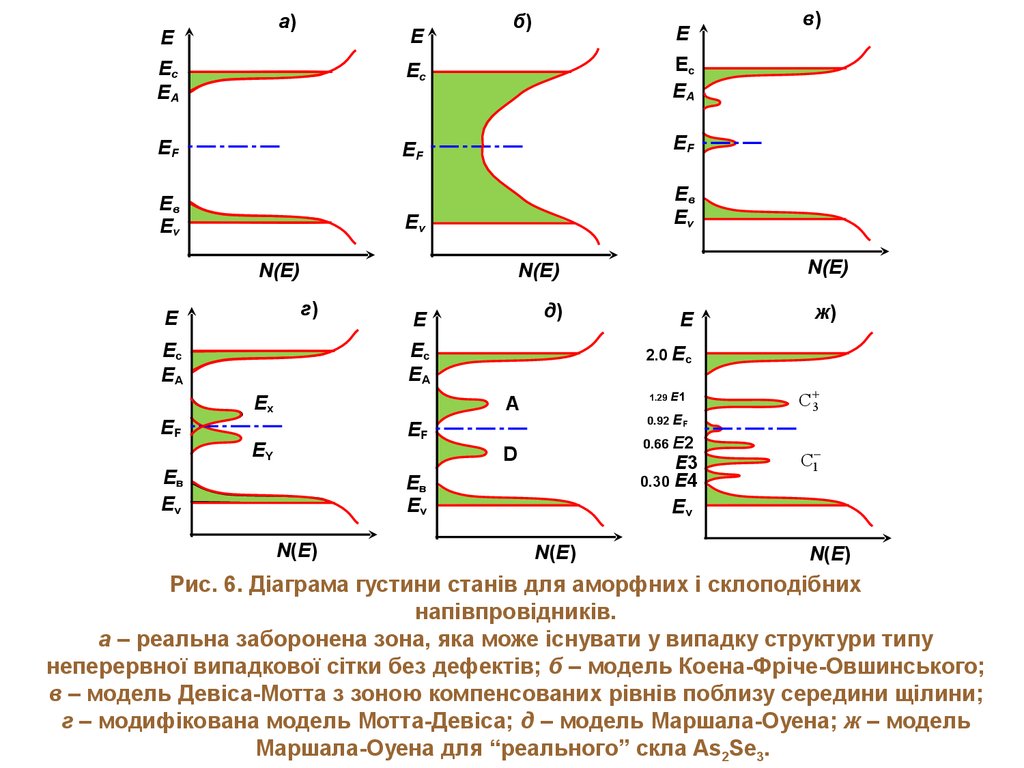
Рис. 6. Діаграма густини станів для аморфних і склоподібних
напівпровідників.
а – реальна заборонена зона, яка може існувати у випадку структури типу
неперервної випадкової сітки без дефектів; б – модель Коена-Фріче-Овшинського;
в – модель Девіса-Мотта з зоною компенсованих рівнів поблизу середини щілини;
г – модифікована модель Мотта-Девіса; д – модель Маршала-Оуена; ж – модель
Маршала-Оуена для “реального” скла As2Se3.
6.
Температурна залежність електропровідності на постійному струміХалькогенідні стекла є напівпровідниками, однією з характерних ознак яких
є дірковий тип провідності. Значення електропровідності в залежності від
складу і структури халькогенідних стекол лежить у межах від 10–2 до
10–16 Ом–1см–1. Процес електричного транспорту в ХСН, де макроскопічна
провідність зумовлена термічним збудженням у речовині, розглядають з
використанням трьох механізмів у залежності від конкретного інтервалу
температур і їх складу.
Ec
EA
а
EF
E gопт
3
1
2
б
EB
Ev
N
Рис. 3. Схема густини станів в ХСН і можливих трьох механізмів
перенесення заряду. 1 – збудження в зонні стани; 2 – збудження в
локалізовані стани в області Елок; 3 – стрибки електронів поблизу
енергії Фермі.
7.
1. Переніс носіїв між делокалізованими станами у зоні провідності (Е Ес) і увалентній зоні (Е Еv); наявність таких станів обумовлено ближнім порядком.
У цьому випадку носії термічним і оптичним шляхом збуджуються за край
рухливості у нелокалізовані стани, тобто стани, розповсюджені по всьому
об’єму тіла, з енергіями Ес і Еv (рис. 3, а). У цьому випадку електропровідність,
яка відповідає переносу носіїв за краями рухливостей, описується
рівнянням:
= o exp [ Ea / kT ]
(1)
У випадку електронної провідності Еа являє собою різницю енергій
нижнього краю зони провідності Ес і рівня Фермі ЕF, E a = Ec E F . При наявності діркової провідності відповідно E a = EF Ev , де Еv – енергія верхньої
границі валентної зони.
Якщо (Ес – ЕF) є лінійною функцією Т в усьому досліджуваному інтервалі
температур, то графік залежностей ln від 1/Т є пряма лінія. У цьому випадку
можна записати:
(2)
Ec E F = E ( 0 ) g ( T )
де Е(0) – величина (Ес – ЕF) при Т = 0 К, а g її температурний коефіцієнт.
Підставляючи (2) у (1), одержимо вираз для провідності по розпростертим
станам:
(3)
= o exp ( g / k ) exp E ( 0 ) / kT = C o exp ( Ea / kT )
(
де Со =eN еф ×mо1 ×exp ( g / k )
)
(Nеф – ефективна густина станів на рівні Ес і Еv).
8.
Стрибковий механізм провідностіЯкщо теплової енергії носія заряду недостатньо, щоб піднятися із
проміжного положення у зону провідності (наприклад, при температурі
нижче за кімнатну), то реалізується стрибковий механізм провідності. У
відповідності з просторовою і енергетичною відстанню між окремими
пастками термічно активовані носії заряду тунелюють від однієї пастки до
іншої. Цей механізм провідності наглядно зображений на рис. 3 стрілками на
рівні енергій ЕА. При такому механізмі переносу заряду провідність
збільшується зі зростанням температури і густини пасток (центрів
захоплення) у матеріалі. У кристалічних напівпровідниках аналогічний
переніс називають провідністю по дефектам.
Провідність, зв’язана з носіями, які збуджуються у локалізовані стани на
краях зон, тобто поблизу ЕА і ЕВ (рис. 3), здійснюється шляхом стрибків і
описується виразом:
(4)
= C1 exp éë ( E A E F W1 / kT ) ùû
де W1 – енергія активації стрибків,
яка повинна зменшуватися зі
зменшенням температури, оскільки по своїй природі провідність має
перескоковий характер зі змінною довжиною стрибка. Провідність по
локалізованим
станам у хвостах дозволених зон характеризуються
активаційною залежністю рухливості:
(5)
m: exp ( - D E / kT )
де Е – різниця енергій рівнів, між якими здійснюється перехід.
9.
Якщо густина станів на рівні Фермі ЕF скінчена, то провідністьодержує вклад від носіїв заряду з енергією поблизу ЕF. Такі носії
можуть здійснювати стрибки між локалізованими станами поблизу
рівня Фермі, як це має місце у процесі домішкової провідності у
сильно легованих і частково компенсованих кристалічних
напівпровідниках. Якщо імовірність визначити як eNеф ×mо1 ×exp ( g / k ) то
згідно Мотта отримуємо (з використанням співвідношення Ейнштейна
m = eD / kT
і виразу D = 1/6 p a2) рівняння типу:
1
s 3 = ea 2nph N ( E F ) exp ( - 2ca ) exp ( - D W2 / kT ) = s o 3exp ( - D W2 / kT ) (6)
6
де N(EF) – густина дефектних станів поблизу рівня Фермі, а N(EF)kT –
число електронів, які приймають участь у провідності. W2 – енергія
активації стрибка, величина якого порядку половини ширини зони
локалізованих станів при умові, що густина станів N(E) має вигляд,
наведений на рис. 3. Відмітимо, що залежність ln від 1/Т буде мати
вигляд прямої тільки якщо стрибки відбуваються між найближчими
сусідами.
10.
При ще більш низьких температурах носії старатимуться стрибнутиза межі своїх просторово самих близьких сусідніх станів у стани з
мінімально можливою різницею енергії. Таким чином, при дуже
низьких температурах можна очікувати, що відбувається провідність
зі змінною довжиною стрибка по локалізованим станам поблизу
рівня Фермі. При такому механізмі переносу заряду справджується
закон Мотта:
1 2 2
1/4
é
= e R N ( E F ) exp ( To / T ) ù
(7)
ë
û
6
16
*
;a
h
2
m
де
- радіус локалізації, 1012 – частота
2
éëa kN ( E F ) ùû
фононів. N(Е) вважається сталою в інтервалі ~ kT. Найбільш імовірна
To
довжина стрибка:
R = éë9a / 8p N ( E F ) kT ùû
1/4
(8)
Врахування усіх трьох механізмів переносу дає наступний вираз для
електропровідності склоподібних напівпровідників:
= C1exp ( E / kT ) C 2 exp éë ( E1 W1 ) / kT ùû C 3exp ( W2 / kT )
(9)
11.
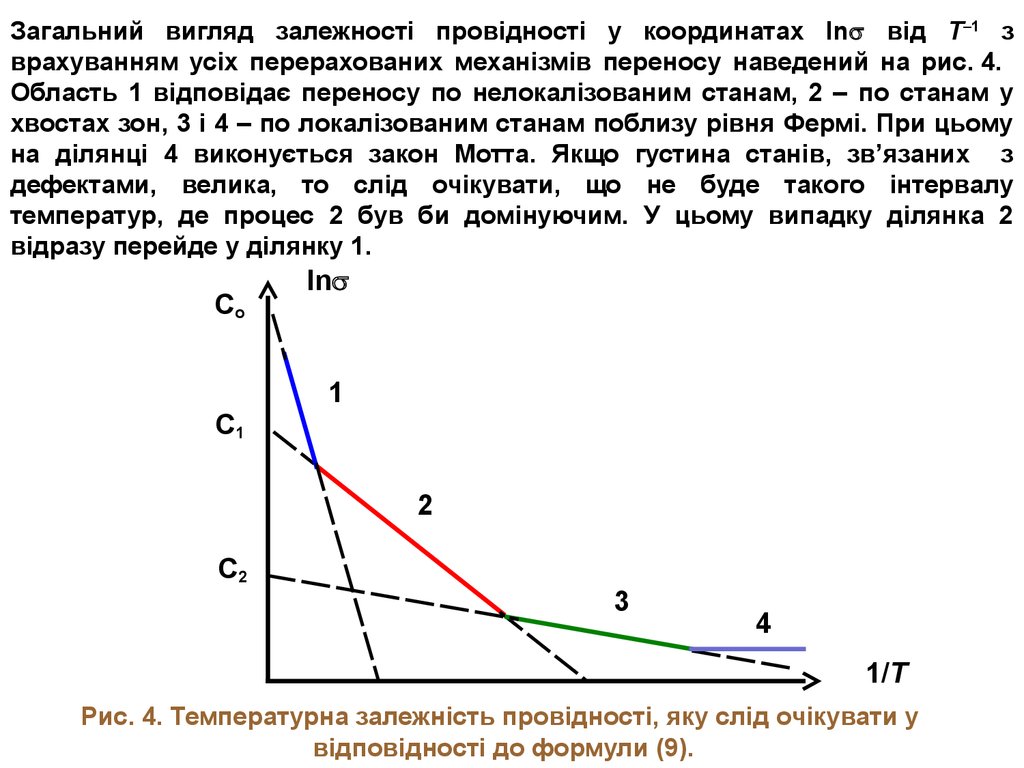
Загальний вигляд залежності провідності у координатах ln від Т–1 зврахуванням усіх перерахованих механізмів переносу наведений на рис. 4.
Область 1 відповідає переносу по нелокалізованим станам, 2 – по станам у
хвостах зон, 3 і 4 – по локалізованим станам поблизу рівня Фермі. При цьому
на ділянці 4 виконується закон Мотта. Якщо густина станів, зв’язаних з
дефектами, велика, то слід очікувати, що не буде такого інтервалу
температур, де процес 2 був би домінуючим. У цьому випадку ділянка 2
відразу перейде у ділянку 1.
Co
ln
1
C1
2
C2
3
4
1/T
Рис. 4. Температурна залежність провідності, яку слід очікувати у
відповідності до формули (9).
12.
GeS2SiO2
Рис. 5. Т-залежність електропровідності ХСН.
13.
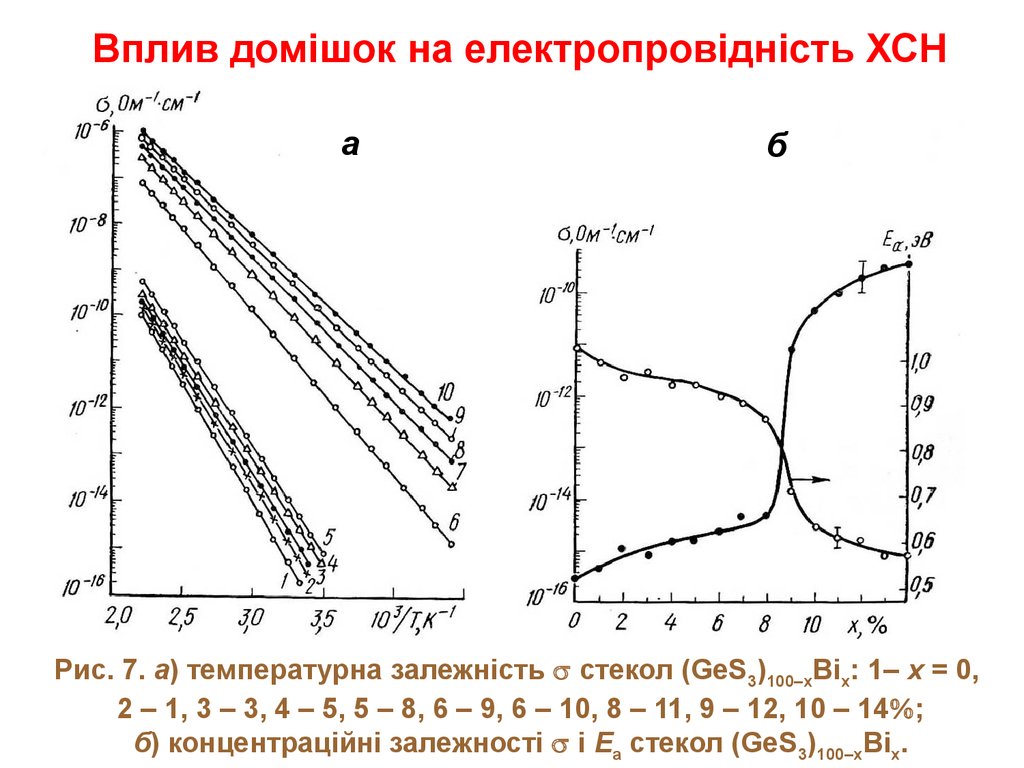
Вплив домішок на електропровідність ХСНа
б
Рис. 7. а) температурна залежність стекол (GeS3)100–xBix: 1– x = 0,
2 – 1, 3 – 3, 4 – 5, 5 – 8, 6 – 9, 6 – 10, 8 – 11, 9 – 12, 10 – 14 ;
б) концентраційні залежності і Еа стекол (GeS3)100–xBix.
14.
Вплив домішок на електропровідність ХСНа
б
Рис. 8. а) залежність (Т) для стекол (Ge2S3)100–xCu(Ag)x: 1– x = 0,
2 – 0.01, 3 – 0.1, 4 – 1, 5 – 2 Cu; 6 – 2 Ag;
б) концентраційні залежності Еа (1,2) і Eg/2 для стекол Ge2S3
легованих Cu (1,3) та Ag (2).
15.
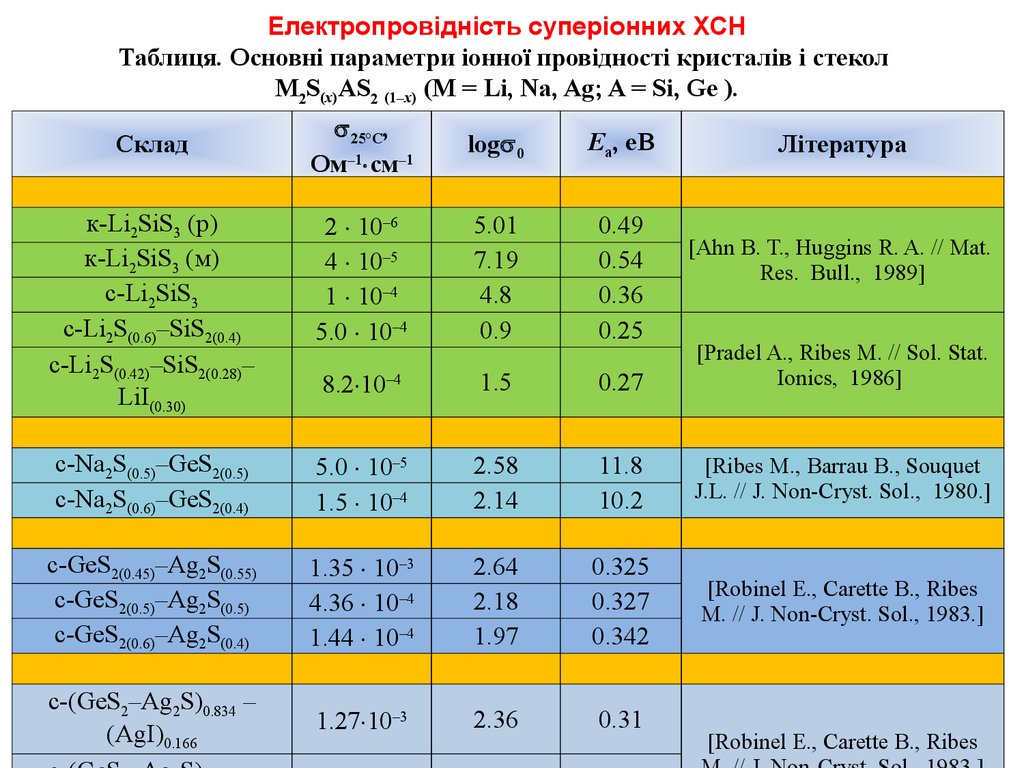
Електропровідність суперіонних ХСНТаблиця. Основні параметри іонної провідності кристалів і стекол
M2S(x)AS2 (1–x) (M = Li, Na, Ag; A = Si, Ge ).
25°C,
Ом–1 см–1
log 0
Еа, еВ
к-Li2SiS3 (р)
к-Li2SiS3 (м)
с-Li2SiS3
с-Li2S(0.6)–SiS2(0.4)
с-Li2S(0.42)–SiS2(0.28)–
LiI(0.30)
2 10–6
4 10–5
1 10–4
5.0 10–4
5.01
7.19
4.8
0.9
0.49
0.54
0.36
0.25
8.2 10–4
1.5
0.27
[Pradel A., Ribes M. // Sol. Stat.
Ionics, 1986]
с-Na2S(0.5)–GeS2(0.5)
с-Na2S(0.6)–GeS2(0.4)
5.0 10–5
1.5 10–4
2.58
2.14
11.8
10.2
[Ribes M., Barrau B., Souquet
J.L. // J. Non-Cryst. Sol., 1980.]
с-GeS2(0.45)–Ag2S(0.55)
с-GeS2(0.5)–Ag2S(0.5)
с-GeS2(0.6)–Ag2S(0.4)
1.35 10–3
4.36 10–4
1.44 10–4
2.64
2.18
1.97
0.325
0.327
0.342
[Robinel E., Carette B., Ribes
M. // J. Non-Cryst. Sol., 1983.]
с-(GeS2–Ag2S)0.834 –
(AgI)0.166
1.27 10–3
2.36
0.31
Склад
Література
[Ahn B. T., Huggins R. A. // Mat.
Res. Bull., 1989]
[Robinel E., Carette B., Ribes
16.
-SiS2Li2S
–Si
–S
–Li
Li2SiS3
кристал
скло
Рис. 9. Проекції кристалічних структур.
17.
β-фаза GeS2Na2S
a
b
–Ge
–S
–Na1
–Na2
Na2GeS3
c
b
Рис. 10. Проекції кристалічних структур.
18.
а)в)
д)
б)
г)
е)
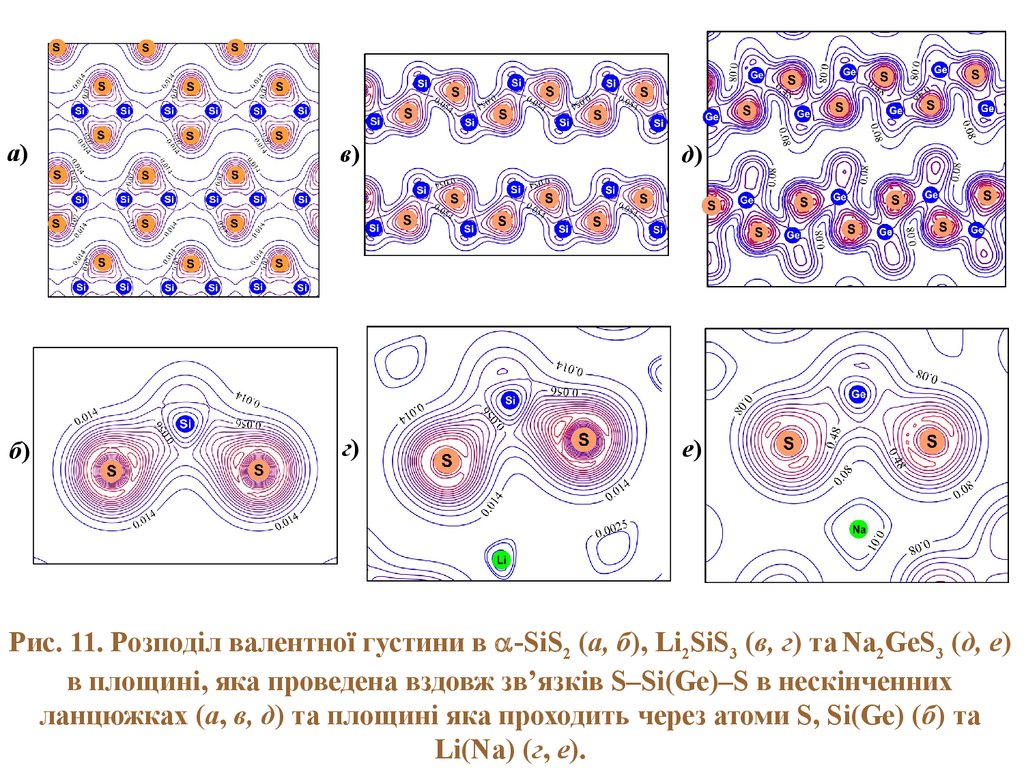
Рис. 11. Розподіл валентної густини в -SiS2 (а, б), Li2SiS3 (в, г) та Na2GeS3 (д, е)
в площині, яка проведена вздовж зв’язків S–Si(Ge)–S в нескінченних
ланцюжках (а, в, д) та площині яка проходить через атоми S, Si(Ge) (б) та
Li(Na) (г, е).
19.
аб
1
3
0
0.7
–3
Li2SiS3(c)
0.36 еВ
2
–1
0.6
–4
0.5
Li2SiS3(м)
1
–3
–4
2.6
0.4
0.54 еВ
–2
–5
Li2SiS3
0.49 еВ
2.8
0.66*
3.0
103/T, K–1
3.2
0.3
3.4
–6
2.
5
3.5
3.
3
–1
0 10 /T, K
Рис. 12. Температурні залежності провідності
кристалічних фаз Li2SiS3 (а) та стекол Li2S(x)SiS2(1–x) (б)
одержаних швидким загартуванням розплаву.
20.
аб
Ea, еВ
1
2.0
0.5
0.4
1.0
0.3
2
0.3
0.4
0.5
0.6
0.3
мол. % Li2S
0.4
0.5
мол. % Li2S
0.6
Рис. 13. Концентраційні залежності: а) log 25 C (крива1) і енергії
активації (крива 2); б) предекспоненціального коефіцієнта провідності
стекол Li2S(x)SiS2(1–x) одержаних швидким загартуванням розплаву
(методом двох валків).
21.
ба
150
50
100
–3
0
40
T,ºC
–50 T,ºC
–30
–3
–4
–4
–5
4
–6
1
2.5
2
3
–5
2
3
103/T, K–1
3
4
1
3.5
3
3.5
4
4.5
103/T, K–1
Рис. 14. Температурна залежність провідності стекол:
а – Na2S(x)GeS2(1–x)(а): 1 – Na2S(0.33)GeS2(0.66); 2 – Na2S(0.42)GeS2(0.58);
3 – Na2S(0.5)GeS2(0.5); 4 –Na2S(0.6)GeS2(0.4).
б – Ag2S(x)GeS2(1–x): 1 – Ag2S(0.3)GeS2(0.7); 2 – Ag2S(0.4)GeS2(0.6); 3 – Ag2S(0.5)GeS2(0.5);
4 – Ag2S(0.55)GeS2(0.45).
22.
ЗарядкаLithium-Ion Battery
Електроліт
Cu
Current
AL
Current
Collector
Collector
Графіт
LiMO2
23.
РозрядкаLithium-Ion Battery
Електроліт
Cu
Current
AL
Current
Collector
Collector
Графіт
LiMO2

















 physics
physics








