Основные понятия формальной логики

1. Основные понятия формальной логики

2.

Формальная логика - наука о формах и законах
мышления. Законы логики отражают в сознании
человека свойства, связи и отношения объектов
окружающего мира. Логика как наука позволяет
строить формальные модели окружающего мира,
отвлекаясь от содержательной стороны.

3.

Высказывание - это любое предложение
какого-либо языка (утверждение),
содержание которого можно определить как
истинное или ложное.
Всякое высказывание или истинно, или
ложно; быть одновременно и тем и другим
оно не может.

4.

Суждения - это форма мышления, в которой утверждается
или отрицается связь между предметом и его признаком,
отношения между предметами или факт существования
предмета и которая может быть либо истинной, либо ложной.
Языковой формой выражения суждения является
повествовательное предложение. Вопросительные и
побудительные предложения суждениями не являются.
Суждения рассматриваются не с точки зрения их смысла и
содержания, а только с точки зрения их истинности или
ложности. Истинным будет суждение, в котором связь понятий
правильно отражает свойства и отношения реальных объектов.
"Дважды два равно четырем" - истинное суждение, а вот
"Процессор предназначен для печати" - ложное. Суждения
могут быть простыми и сложными. "Весна наступила, и грачи
прилетели" - сложное суждение, состоящее из двух простых.
Простые суждения (высказывания) выражают связь двух
понятий. Сложные - состоят из нескольких простых суждений

5.

Умозаключение - прием мышления, позволяющий на
основе одного или нескольких суждений-посылок получить
новое
суждение
(знание
или
вывод).
Примерами умозаключений являются доказательства
теорем в геометрии. Посылками умозаключения по
правилам формальной логики могут быть только истинные
суждения. Тогда и умозаключение будет истинным. Иначе
можно прийти к ложному умозаключению.

6.

Логические величины--понятия, выражаемые словами:
ИСТИНА, ЛОЖЬ (true, false).
Следовательно, истинность высказываний
выражается,через логические величины.

7.

Логическое выражение - это символическая запись
высказывания, состоящая из логических величин
(констант или переменных), объединенных логическими
операциями (связками).
Связки "НЕ", "И", "ИЛИ" заменяются логическими
операциями инверсия, конъюнкция, дизъюнкция. Это
основные логические операции, при помощи которых
можно записать любое логическое выражение.

8.

Конъюнкция - логическое умножение (от латинского conjunctio - союз, связь):
• в естественном языке соответствует союзу «И»
;
• в алгебре высказываний обозначение «&»
;
• в языках программирования обозначение «And».
Конъюнкция - это логическая операция, ставящая в соответствие каждым двум
простым (или исходным) высказываниям составное высказывание, являющееся
истинным тогда и только тогда, когда оба исходных высказывания истинны. Если
хотя бы одно из составляющих высказываний ложно, то и полученное из них с
помощью союза «И» сложное высказывание также считается ложным.

9.

Дизъюнкция - логическое сложение (от латинского disjunctio - разобщение,
различие):
• в естественном языке соответствует союзу «ИЛИ»
;
• в алгебре высказываний обозначение «V» или «+»
;
• в языках программирования обозначение «Or».
Дизъюнкция - это логическая операция, которая каждым двум простым (или
исходным) высказываниям ставит в соответствие составное высказывание,
являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны
и истинным, когда хотя бы одно из двух образующих его высказываний истинно

10.

Инверсия - отрицание (от латинского disjunctio - разобщение, различие):
• в естественном языке соответствует словам «неверно, что...» и частице
«не»
;
• в алгебре высказываний обозначение «¬» или «-»
;
• в языках программирования обозначение «Not».
Отрицание - логическая операция, которая с помощью связки «не» каждому
исходному высказыванию ставит в соответствие составное высказывание,
заключающееся в том, что исходное высказывание отрицается.

11.

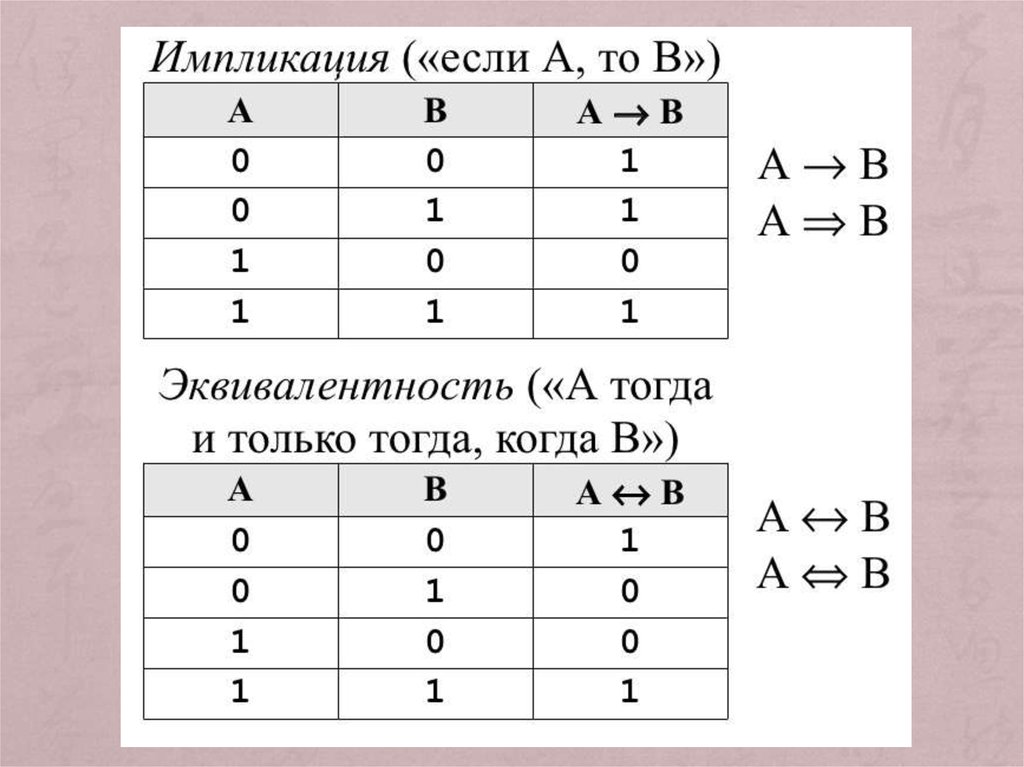
Логическое следование (импликация):
Высказывание, составленное из двух
высказываний при помощи связки «если ..., то
...», называется логическим следованием,
импликацией (импликация от латинского
implico - тесно связываю).
Эквивалентность (логическое тождество):
Высказывание, составленное из двух
высказываний при помощи связки «тогда и
только тогда, когда», называется
эквивалентностью (эквивалентность логическое тождество, равнозначность,
взаимная обусловленность. )

12.

13. Примеры:

+ Пример 1. Определить участника преступления, исходя из
двух посылок:
1) "Если Иванов не участвовал или Петров участвовал, то
Сидоров участвовал";
2) "Если Иванов не участвовал, то Сидоров не участвовал".
Решение
Составим выражения:
I - "Иванов участвовал в преступлении";
P - "Петров участвовал в преступлении";
S - "Сидоров участвовал в преступлении".
Запишем посылки в виде формул:
Тогда
+ Проверим результат, используя таблицу истинности:
+

14.

Ответ: Иванов участвовал в преступлении.

15.

1.
Выберите пример, являющийся высказыванием:
a) «Не могли бы вы передать мне соль?»
b) «Н. В. Гоголь писал «Мертвые души» в Риме.»
c) «Солнце есть спутник Земли.»
d) «Некоторые лекарства опаснее самих болезней»
e) «Сегодня замечательная погода!»
2) Запишите высказывания в виде логических выражений
1.число 17 нечетное и двухзначное, и простое
2.Неверно, что корова – хищное животное
3.Если Маша – сестра Саши, то Саша – брат Маши
4.Если компьютер включен, то можно на нем работать
5.Водительские права можно получить права тогда и только
тогда, когда тебе исполнится 18 лет