Similar presentations:
Реализация бинарных деревьев на Си
1. ПРОГРАММИРОВАНИЕ
Семинар 12.Деревья, графы
Новосибирский государственный университет, 2019
2. Реализация бинарных деревьев на Си
typedef struct node {char *word;
struct node *left;
struct node * right;
} tree;
void print_tree(tree *t)
{
if (!t) return;
print_tree(t -> left);
printf("%s\n", t -> word);
print_tree(t -> right);
}
Семинар 12. Деревья, графы
3. Сбалансированные деревья
Дерево называется сбалансированным,если высоты двух поддеревьев
каждой из его вершин отличаются не
более, чем на единицу.
АВЛ-дерево — сбалансированное
двоичное дерево поиска.
(Адельсон-Вельский, Ландис, 1962 г.)
Семинар 12. Деревья, графы
4. Теорема
Среднее число сравнений,необходимых для вставки n случайных
элементов в дерево двоичного поиска,
пустое в начале, равно O(n log2 n) для
n ≥ 1.
Максимальное число сравнений — O(n2).
Семинар 12. Деревья, графы
5. Вставка элемента в сбалансированное дерево
r1. hL = hR
2. hL < hR
3. hL > hR
hL
1
Семинар 12. Деревья, графы
L
hR
R
6. Вставка в левое поддерево
AB
B
A
3
1
2
Семинар 12. Деревья, графы
1
2
3
7. Вставка в правое поддерево
CA
B
A
B
1
2
3
4
Семинар 12. Деревья, графы
1
C
2
3
4
8. Представление графов
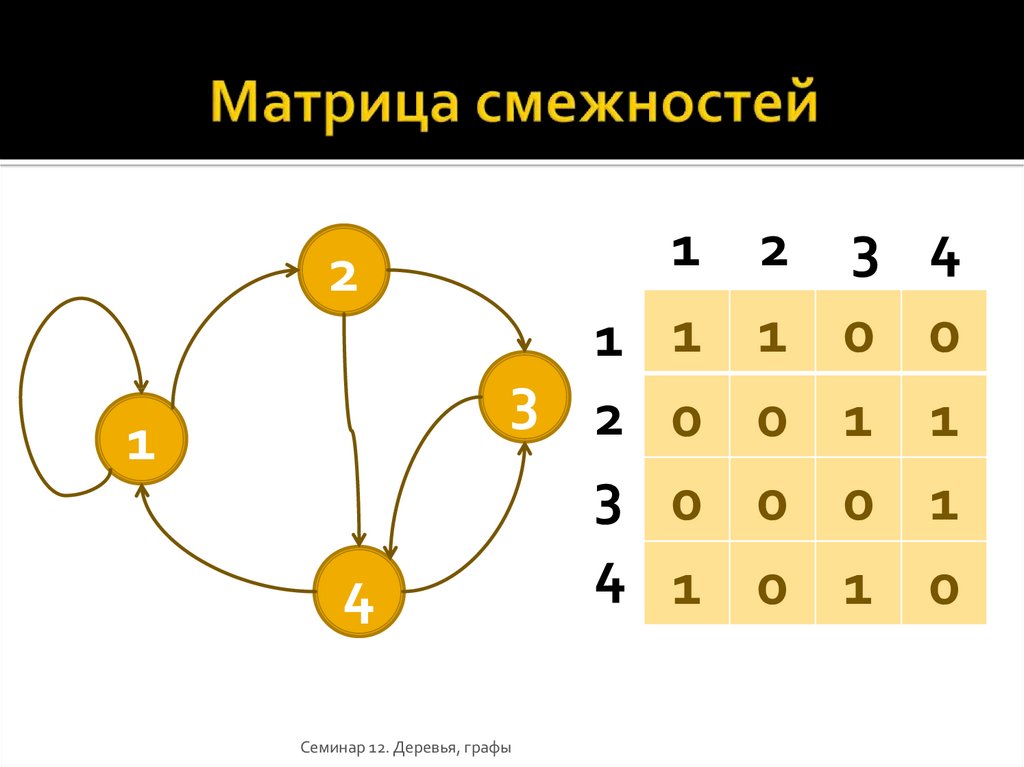
Семинар 12. Деревья, графы9. Матрица смежностей
21
4
1
3 2
3
4
Семинар 12. Деревья, графы
1
1
0
0
1
2
1
0
0
0
3
0
1
0
1
4
0
1
1
0
10. Матрица инцидентностей
13
2
2
4
1
6
3
5
1 2 3 4 5 6 7
7
4
Семинар 12. Деревья, графы
1
2
3
4
1 1 0 0 0 -1 0
0 -1 1 1 0 0 0
0 0 -1 0 1 0 -1
0 0 0 -1 -1 1 1
11. Списки смежностей
23
1
4
Семинар 12. Деревья, графы
1
1
2
NULL
2
3
4
NULL
3
4
NULL
4
1
3
NULL
12. Частичный порядок
Определение?Семинар 12. Деревья, графы
13. Частичный порядок
Отношение R на множестве A:∀a∈ A ¬aRa;
∀a, b, c∈ A aRb & bRc⇒ aRc.
Следствие: ∀a, b∈ A aRb⇒ ¬bRa.
Семинар 12. Деревья, графы
14. Частичный порядок: примеры
решение большой задачиразбивается на ряд подзадач;
последовательность чтения тем в
учебном курсе;
выполнение работ: одну следует
выполнить раньше другой;
и т. п.
Семинар 12. Деревья, графы
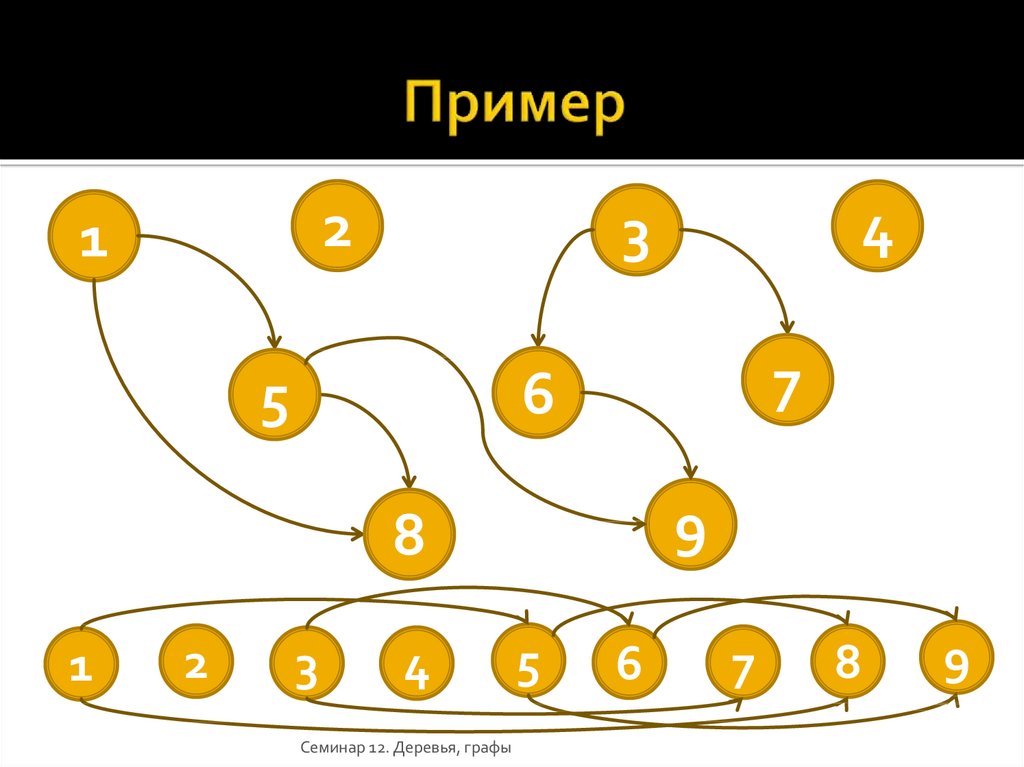
15. Пример
21
4
3
7
6
5
8
Семинар 12. Деревья, графы
9
16. Линейный порядок
Определение?Семинар 12. Деревья, графы
17. Линейный порядок
∀a, b∈ A aRb либо bRa либо a = b.Семинар 12. Деревья, графы
18. Пример
21
7
6
5
9
8
1
2
4
3
3
4
Семинар 12. Деревья, графы
5
6
7
8
9
19. Алгоритм топологической сортировки
Вход: частичный порядок R на конечном множествеA = {a1, a2, …, an}.
Выход: линейный порядок R' на A: R⊆ R'.
Метод: представить R' в виде списка Ln = a1, a2, …, an,
для которого aiR'aj при i < j.
Шаг 1: положить i = 1, A1 = A, R1 = R.
Шаг 2: если Ai пусто, то остановиться и выдать
Li = a1, a2, …, ai в качестве R'.
Иначе выбрать в Ai такой ai + 1, что ∀a'∈ A ¬a'Rai + 1.
Шаг 3: положить Ai + 1 = Ai \ {ai + 1}, Ri + 1 = Ri \ ({ai + 1}× Ai + 1),
i++, на шаг 2.
Семинар 12. Деревья, графы
20. Алгоритм топологической сортировки
Реализация на матрице смежности:1. Найти вершину, в которую не входит
ни одна дуга (нулевой столбец).
2. Удалить все исходящие из неё дуги
(обнулить соответствующую строку).
3. Пока не перебрали все вершины,
повторять сначала.
Семинар 12. Деревья, графы
21. Пути в графах
Семинар 12. Деревья, графы22. Определения
Пусть G = (V, E) — ориентированный граф.Поставим в соответствие каждой дуге e∈ E в
графе G неотрицательную стоимость c(e).
c: E→ R+ — функция стоимости.
Стоимость пути определяется как сумма
стоимостей образующих его дуг.
Задача о нахождении кратчайшего пути состоит в
нахождении для каждой пары узлов (v, w) пути
наименьшей стоимости.
Семинар 12. Деревья, графы
23. Нахождение кратчайшего пути из одного источника
Идея: строится множество S, содержащее вершиныграфа, кратчайшие расстояния до которых от
источника известны. На каждом шаге
добавляется тот из оставшихся узлов,
кратчайшее расстояние до которого меньше всех
других оставшихся узлов (т. н. "жадный"
алгоритм).
Семинар 12. Деревья, графы
24. Алгоритм Дейкстры
Вход: ориентированный граф G = (V, E),источник v0∈ V,
функция стоимости c: E→ R+.
Полагаем, что
c(vi, vj) = +∞, если (vi, vj)∉ E;
c(v, v) = 0.
Выход: для всех вершин v∈ V наименьшая сумма
стоимостей дуг из E, взятая по всем путям,
идущим из v0 в v.
Семинар 12. Деревья, графы
25. Алгоритм Дейкстры
Метод: строим такое множество S⊆ V, чтократчайший путь из источника в каждый узел
v∈ S целиком лежит в S.
Массив D[v] содержит стоимость текущего
кратчайшего пути из v0 в v.
Семинар 12. Деревья, графы
26. Алгоритм Дейкстры
{S = {v0};
D[v0] = 0;
для всех v∈ V \ {v0} выполнить: D[v] = c(v0, v);
пока S ≠ V выполнять:
{
выбрать узел w∈ V \ S, для которого D[w] принимает
наименьшее значение;
S = S∪ {w};
для всех v∈ V \ S выполнить
D[v] = min(D[v], D[w] + c(w, v));
}
}
Семинар 12. Деревья, графы
27. Пример
21
0
10
S
3
6
7
4
3
5
2
4
w
D[w]
D[1]
D[2]
D[3]
D[4]
{0}
-
-
2
+∞
+∞
10
{0, 1}
1
2
2
5
+∞
9
{0, 1, 2}
2
5
2
5
9
9
{0, 1, 2, 3}
3
9
2
5
9
9
{0, 1, 2, 3, 4}
4
9
2
5
9
9
Семинар 12. Деревья, графы
28. Нахождение кратчайших путей между всеми парами вершин
Строим матрицу стоимостей:c(i, j), если дуга (i, j)∈ E;
M[i, j] =
+∞ , если дуга (i, j)∉ E;
0, если i = j.
Обозначим через d[i, j] матрицу кратчайших путей
между всеми вершинами.
Вершины занумеруем числами от 1 до n.
Семинар 12. Деревья, графы
29. Алгоритм Флойда-Уоршелла
Обозначим через dij(k) стоимость кратчайшего пути извершины с номером i в вершину с номером j с
промежуточными вершинами из множества {1, 2, …, k}.
M[i, j], если k = 0,
dij(k) =
min(dij(k - 1), dik(k - 1) + dkj(k - 1)), если k ≥ 1.
D(n) содержит искомое решение.
Семинар 12. Деревья, графы
30. Алгоритм Флойда-Уоршелла
Floyd-Warshall(M, n){
D(0) = M;
for k = 1 to n do
for i = 1 to n do
for j = 1 to n do
dij(k) = min(dij(k - 1), dik(k - 1) + dkj(k - 1));
return D(n);
}
Семинар 12. Деревья, графы
31. Транзитивное замыкание графа
Транзитивное замыкание орграфа G = (V, E) —орграф G' = (V, E'), в котором (v, w)∈ E' ⇔
существует путь (длины 0 или больше) из v в w в G.
Семинар 12. Деревья, графы
32. Пример
21
5
2
3
4
1
5
4
Семинар 12. Деревья, графы
3
33. Построение транзитивного замыкания графа
Обозначим через tij(k) наличие пути из вершины с номером i ввершину с номером j с промежуточными вершинами из
множества {1, 2, …, k}. M — матрица смежностей G.
M[i, j], если k = 0,
tij(k) =
tij(k - 1)∨ (tik(k - 1) & tkj(k - 1)), если k ≥ 1.
T(n) содержит искомое решение.
Семинар 12. Деревья, графы
34. Построение транзитивного замыкания графа
Transitive_Closure(M, n){
T(0) = M;
for k = 1 to n do
for i = 1 to n do
for j = 1 to n do
tij(k) = tij(k - 1)∨ (tik(k - 1) & tkj(k - 1));
return T(n);
}
Семинар 12. Деревья, графы
































 programming
programming








