Similar presentations:
Задачи по теме «Расчеты пути на прочность и устойчивость»
1.
Задачи по теме «Расчеты пути на прочностьи устойчивость»
3.7 Определить среднюю величину, среднее квадратическое отклонение
и максимально вероятную величину расчетной нагрузки от колеса на рельс,
если статическая нагрузка от веса экипажа на колесо Pст = 143139 Н, а
ср
P
среднее значение силы инерции от колебания кузова на рессорах р =
15592 Н, среднее квадратическое отклонение нагрузки от колебания
надрессорного строения Sр = 3598 Н, от сил инерции необрессоренных масс,
вызванных: неровностью на пути Sнп = 8209 Н, изолированной неровностью
на колесе Sинк = 15363 Н, непрерывной неровностью на колесе Sннк = 1330 Н.
2.
Средняя величина расчетной нагрузки –;
Среднее квадратическое отклонение расчетной нагрузки –
Максимально вероятная величина расчетной нагрузки –
;
.
3.
Решение задачиСреднее значение расчетной нагрузки от колеса на рельс определяется
по формуле
ср
Pрасч
Pст Pрср .
(1)
Здесь Pст – статическая нагрузка колеса на рельс;
Pрср – среднее значение динамической добавки от колебания кузова на
рессорах.
ср
Pрасч
143139 15592 158731 Н.
q1 = 0,05
Расчетная нагрузка определяется по формуле
ср
Pрасч Pрасч
ф Sрасч ,
(3)
2
2
2
S расч S р2 Sнп
(1 q1 ) Sннк
q1Sинк
.
(2)
Численные значения Pрасч и Sрасч составят
Sрасч 3598 2 8209 2 (1 0,05) 1330 2 0,05 15363 2 9687 Н;
Pрасч 158731 2,5 9687 182946 Н.
4.
Решить задачу 3.7 при следующих исходных данных:− Pcт= 135000 Н;
− Pсрр = 12000 Н;
1)
− Sр = 3000 Н;
− Sнп = 7500 Н;
− Sинк = 11700 Н;
2)
3)
− Sннк = 1000 Н.
Pрасчср = 135000+12000=147000 Н;
Sрасч = (30002 + 75002 + 0,95 · 10002 +0,05 ·117002) взять корень = 8547Н;
Pрасч = 147000 + 2,5·8547 = 168367 Н.
5.
IP
3.8
Определить эквивалентную нагрузку экв от колес
двухосной тележки с расстояниями между осями l1 = 1,85 м и
l2 = 6,75 м на рельс для определения изгибающего момента
ср
при средней величине расчетной нагрузки Pрасч
= 158731 Н,
величине среднего квадратического отклонение расчетной
нагрузки S расч = 9687 Н и коэффициента относительной
жесткости подрельсового основания и рельса k = 1,421 м-1.
6.
Решение задачиОпределим вначале Pрасч по формуле
ср
Pрасч Pрасч
ф S расч ;
(1)
Pрасч 158731 2,5·9687 182946 Н .
Максимальная эквивалентная нагрузка
напряжений в рельсах определяется по формуле
для
I
Pэкв
Pрасч (kxi ) Pi ср ,
где
расчета
изгибных
(4)
(kxi ) – ординаты линии влияния изгибающих моментов рельса в
сечениях пути xi, расположенных под колесными нагрузками тележки Pi
ср
на
расстоянии xi от, смежных с расчетной осью
(kxi ) e kxi (cos( kxi ) sin( kxi )).
(3)
Расчет ведется для системы, состоящей из трех колесных нагрузок.
Для этого случая координаты средних нагрузок равны x1 = l1, x2 = l1 + l2. (2)
Причем для двухосной тележки l2 –– это расстояние между крайней осью
первой тележки и первой осью следующей по ходу поезда тележки.
7.
8.
Решить данную задачу при следующих исходныхданных:
Pрасчср = 120 000 Н;
Sрасч = 8 500 Н;
l1 = 1,85 м; l2 = 6,75 м;
k = 1,421 м-1.
1. Pрасч = Pрасчср + 2,5· Sрасч = 120 000 + 2,5·8 500 =
= 141 250 Н.
2. x1 = l1 = 1,85 м; x2 = l1 + l2 = 1,85 + 6,75 = 8,6 м.
9.
3.степень, не забывать про знак «–»
μ(kx1)
1) kx1 = 1,421·1,85 = 2,62885;
2) e-2,62885 = 2,718282 нажать знак степени -2,62885
= 0, 072 161;
3) включить вычисление в радианах!
(проверка cos(3,14) ≈ -1)
4) cos(1,421·1,85) = cos(2,62885) = -0,871402;
5) sin(1,421·1,85) = sin(2,62885) = 0,490569;
6) μ(kx1) = μ(1,421·1,85) = 0,072161·(-0,871402 – 0,490569)
= -0,098281.
10.
μ(kx2)1) kx2 = 1,421·8,6 = 12,2206;
2) e-12,2206 = 2,718282 нажать знак степени -12,2206 =
= 0, 000 0049;
3) включить вычисление в радианах!
(проверка cos(3,14) ≈ -1)
4) cos(1,421·8,6) = cos(12,2206) = 0,940815;
5) sin(1,421·8,6) = sin(12,2206) = -0,338922;
смена знака «-» на «+»
6) μ(kx1) = μ(1,421·1,85) = 0,0000049·(0,940815+0,338922)
= 0,0000063.
11.
Pэкв1 = Pрасч + (μ(kx1) + μ(kx2))·Pрасчср == 141250 +(-0,098281+0,0000063)·120000 =
= 129457 Н.
12.
IIP
3.9
Определить эквивалентную нагрузку экв от колес
двухосной тележки с расстояниями между осями l1 = 1,85 м и l2
= 6,75 м на рельс для определения прогиба рельса и нагрузки
ср
рельса на шпалу при средней величине расчетной нагрузки Pрасч
= 158731 Н, величине среднего квадратического отклонение
расчетной нагрузки S расч = 9687 Н и коэффициента
относительной жесткости подрельсового основания и рельса k =
1,421 м-1.
13.
Решение задачиМаксимальная величина эквивалентной нагрузки определяется по
формуле
II
Pэкв
Pрасч (kxi ) Pi ср ,
4)
где ( kxi ) – ординаты линии влияния давлений рельса на шпалы в сечениях
пути xi, расположенных под колесными нагрузками Pi ср на расстоянии xi от
осей тележки, смежных с расчетной осью
знак «+»
(kxi ) e kxi (cos( kxi ) sin( kxi )). 3)
ср
В этом случае при расчете PэкII координаты средних нагрузок Pi равны
x1 = l1, x2 = l2. 2)
Определим вначале Pрасч по формуле
ср
Pрасч Pрасч
ф S расч ;
1)
Pрасч 158731 2,5·9687 182946 Н .
14.
Ординаты линии влияния давления рельса на шпалу определяютсяследующим образом
(kx1 ) (1,421 1,85) e 1, 421 1,85 (cos(1,421 1,85) sin(1,421 1,85)) 0,027481;
(kx1 ) (1,421 6,75) e 1, 421 6,75 (cos(1,421 6,75) sin(1,421 6,75)) 0,000079 .
Максимальная величина эквивалентной нагрузки для определения
давления рельса на шпалу:
II
Pэкв
182946 0,027481 158731 0,000079 158731 178577 Н.
15.
Решить данную задачу при следующих исходныхданных:
Pрасчср = 120 000 Н;
Sрасч = 8 500 Н;
l1 = 1,85 м; l2 = 6,75 м;
k = 1,456 м-1.
Рэкв2 = 137 442 Н.
16.
3.10 Определить напряжения изгиба в подошве рельса:осевые σпо и кромочные σпк при воздействии эквивалентной
I
нагрузки Pэкв
= 167356 Н, коэффициенте относитлеьной
жесткости подрельсового основания и рельса k = 1,4214 м-1,
моменте сопротивления поперечного сечения рельса
относительно подошвы Wп = 417·10-6 м3, коэффициенте
учета внецентренного приложения вертикальных и
горизонтальных поперечных сил f = 1,33.
17.
Решение задачиНормальные изгибные напряжения в подошве рельса находятся по
общеизвестной формуле
M
по
,
Wп
где М – изгибающий момент;
Wп – момент сопротивления относительно наиболее удаленного волокна.
Напряжения в кромке подошвы рельса пк определяется по формуле
σ пк f σ по .
Здесь:
f – коэффициент, переводящий осевые напряжения в подошве в
кромочные напряжения; он учитывает влияние горизонтальных поперечных
сил Н и внецентренное приложение вертикальных сил Р.
18.
Изгибающий момент в рельсе от воздействия эквивалентной нагрузкиI
Pэкв
I
Pэкв
167356
M
29443 Н м. 1)
4k 4 1,4214
Осевые изгибные напряжения в подошве рельса
29443 10 6
по
70,6 МПа.
6
417 10
Изгибные напряжения в кромке подошвы рельса
пк 1,33 70,6 93,9 МПа.
2)
3)
19.
Решить данную задачу при следующих исходныхданных:
Pэкв1 = 120 000 Н;
k = 1,4214 м-1 ;
Wп = 417·10-6 м3;
f = 1,52.
σпо = 54,6 МПа, σпк = 83,0 МПа.
20.
3.11 Определить напряжения изгиба в подошве рельса:осевые σпо и кромочные σпк от воздействия колес двухосной
тележки с расстоянием между осями l = 1,85 м, если
величина расчетной нагрузки Pрасч = 182946 Н, средняя
ср
величина расчетной нагрузки Pрасч
= 158731 Н, коэффициенте
относительной жесткости подрельсового основания и рельса
k = 1,4214 м-1, момент сопротивления поперечного сечения
рельса относительно подошвы Wп = 417·10-6 м3,
коэффициент учета внецентренного приложения
вертикальных и горизонтальных поперечных сил f = 1,33.
21.
Решение задачиНормальные изгибные напряжения в подошве рельса находятся по
общеизвестной формуле
M
5)
по
,
Wп
где М – изгибающий момент;
Wп – момент сопротивления относительно наиболее удаленного волокна.
Напряжения в кромке подошвы рельса пк определяется по формуле
σ пк f σ по .
6)
Здесь:
f – коэффициент, переводящий осевые напряжения в подошве в
кромочные напряжения; он учитывает влияние горизонтальных поперечных
сил Н и внецентренное приложение вертикальных сил Р.
22.
Изгибающий момент в рельсе от воздействия эквивалентной нагрузкиI
Pэкв
определяется по формуле
I
Pэкв
M
. 4)
4k
Максимальная эквивалентная нагрузка
напряжений в рельсах определяется по формуле
для
расчета
изгибных
I
Pэкв
Pрасч (kxi ) Pi ср , 3)
где
(kxi ) – ординаты линии влияния изгибающих моментов рельса в
сечениях пути xi, расположенных под колесными нагрузками тележки Pi
ср
на
расстоянии xi от, смежных с расчетной осью
(kxi ) e kxi (cos( kxi ) sin( kxi )). 2)
Для заданных условий координаты средних нагрузок равны x1 = l1, x2 =
l1 + l2. Причем для двухосной тележки l2 – это расстояние между крайней
осью первой тележки и первой осью следующей по ходу поезда тележки.
Значения расстояний l1 и l2 для четырехосного грузового вагона
x1 = l1 = 1,85 м; x2 = l1 + l2 = 1,85 + 6,75 = 8,6 м. 1)
23.
Ординаты линии влияния изгибающих моментов рельса(kx1 ) (1,421 1,85) e 1, 421 1,85 (cos(1,421 1,85) sin( 1,421 1,85)) 0,098282;
2)
(kx 2 ) (1,421 8,6) e 1, 421 8,6 (cos(1,421 8,6) sin(1,421 8,6)) 0,000063 .
Максимальная эквивалентная нагрузка для расчетов напряжений в
рельсах от изгиба определяется
3)
I
Pэкв
182946 0,098282 158731 0,000063 158731 167356 Н.
Изгибающий момент в рельсе от воздействия эквивалентной нагрузки
I
Pэкв
I
Pэкв
167356
4)
M
29443 Н м.
4k 4 1,4214
Осевые изгибные напряжения в подошве рельса
29443 10 6
70,6 МПа.
5) по
6
417 10
Изгибные напряжения в кромке подошвы рельса
6) пк 1,33 70,6 93,9 МПа.
24.
Решить данную задачу при следующих исходныхданных:
Pрасч = 150000 Н;
Pрасчср = 120 000 Н;
k = 1,4214 м-1 ;
l1 = 1,85 м;
l2 = 6,75 м;
Wп = 417·10-6 м3;
f = 1,52.
σпо = 58,3 МПа, σпк = 88,6 МПа.
25.
26.
Решение задачиВ начале определим расчетную нагрузку от колеса на рельс
ср
Pрасч Pрасч
ф Sрасч . 1)
Для заданных условий
Pрасч 158731 2,5·9687 182946 Н .
Напряжения смятия в деревянных шпалах под подкладками и в
прокладках при железобетонных шпалах определяются по формуле
Q
ш , 5)
где Q – давление колеса на рельс;
– площадь передачи давления на шпалу через подкладку или
прокладку (при бесподкладочном скреплении типа ЖБР).
Напряжения в балластном слое под шпалой в подрельсовом сечении
определяется по формуле
Q
Q
б
, 6)
0,5 ab
где 0,5аb – площадь полушпалы (а и b – длина и ширина шпалы);
α – коэффициент изгиба шпалы;
Ωα – эффективная площадь полушпалы с учетом изгиба.
27.
Давление колеса на рельс определяется по формулеII
Pэкв
klш
4)
Q
.
2
Максимальная величина эквивалентной нагрузки определяется по
формуле
II
Pэкв
Pрасч (kxi ) Pi ср ,
3)
где ( kxi ) – ординаты линии влияния давлений рельса на шпалы в сечениях
пути xi, расположенных под колесными нагрузками Pi ср на расстоянии xi от
осей тележки, смежных с расчетной осью
(kxi ) e kxi (cos( kxi ) sin( kxi )). 2)
28.
IIср
При расчете Pэкв координаты средних нагрузок Pi равны x1 = l1, x2 = l2.
Подставив численные значения в приведенные здесь формулы,
определим напряжения в элементах верхнего строения пути.
(kx1 ) (1,421 1,85) e 1, 421 1,85 (cos(1,421 1,85) sin(1,421 1,85)) 0,027481;
(kx1 ) (1,421 6,75) e 1, 421 6,75 (cos(1,421 6,75) sin(1,421 6,75)) 0,000079 .
II
Pэкв
182946 0,027481 158731 0,000079 158731 178571 Н.
178571 1,4214 0,50
Q
63437 Н.
2
63437 10 6
ш
3,02 МПа.
4
210 10
63437 10 6
б
0,213 МПа.
4
2975 10
29.
Решить данную задачу при следующих исходныхданных:
Sрасч = 8500 Н;
Pрасчср = 120 000 Н;
k = 1,4214 м-1 ;
l1 = 1,85 м;
l2 = 6,75 м;
lш = 0,5 м;
ω = 210·10-4 м2;
Ω = 2975·10-4 м2.
σш = 2,33 МПа, σб = 0,165 МПа.
30.
31.
Решение задачиНапряжения смятия в деревянных шпалах под подкладками и в
прокладках при железобетонных шпалах определяются по формуле
Q
ш , 2)
где Q – давление колеса на рельс;
– площадь передачи давления на шпалу через подкладку или
прокладку (при бесподкладочном скреплении типа ЖБР).
Напряжения в балластном слое под шпалой в подрельсовом сечении
определяется по формуле
Q
Q
б
, 3)
0,5 ab
где 0,5аb – площадь полушпалы (а и b – длина и ширина шпалы);
α – коэффициент изгиба шпалы;
Ωα – эффективная площадь полушпалы с учетом изгиба.
32.
Давление колеса на рельс определяется по формулеII
Pэкв
klш
Q
. 1)
2
Подставив численные значения в приведенные здесь формулы,
определим напряжения в элементах верхнего строения пути.
178571 1,4214 0,50
63437 Н.
2
63437 10 6
ш
3,02 МПа.
4
210 10
63437 10 6
б
0,213 МПа.
4
2975 10
Q
33.
3.14 Поезд движется по спуску крутизной i = 5 ‰ и по кривой R = 500 м,основное сопротивление движению вагонов ω’’0 = 1,7 Н/кН. Определить
суммарное сопротивление движению вагонов.
34.
3.15 Определить поперечную составляющую продольной силы впоезде, действующую наружу кривой R = 600 м, если величина
продольной силы в автосцепке N = 600 кН.
Решение задачи
Поперечная составляющая продольной силы в поезде ΔH определяется
по формуле
H
3600 N
3600 N
6,96
3600·600
6,96
0,028
0
,
028
3600 600
28,5 кН .
R
600
35.
3.16 Определить устойчивость колеса на рельсе в кривой при величиненагрузок от колес на рельсы P = 110 кН, величине рамной силы Ур = 80 кН
и величине непогашенного поперечного ускорения αн = 0,3 м/с2.
Решение задачи
Коэффициент запаса устойчивости колеса на рельсе определяется по
формуле
Pн Pв
.
0,44У р 0,4 Pн 0,85Pв
Нагрузки на наружный и внутренний рельсы кривой определяются по
формулам
Pн Q(0,25 0,127 н );
Pв Q(0,25 0,127 н ),
где Q – вес вагона, приходящийся на одну ходовую тележку Q = 4P = 4·110 =
440 кН.
36.
ТогдаPн 440(0,25 0,127 0,3) 126,76 кН;
Pв 440(0,25 0,127 0,3) 93,24 кН .
Проверка (126,76+93,24)/2=110 кН.
Подставив полученные значения в первую формулу, получим
126,76 93,24
220
1,33 1,0.
0,44·80 0,4·126,76 0,85·93,24 165,15
В заданных условиях колесо устойчиво на рельсе.










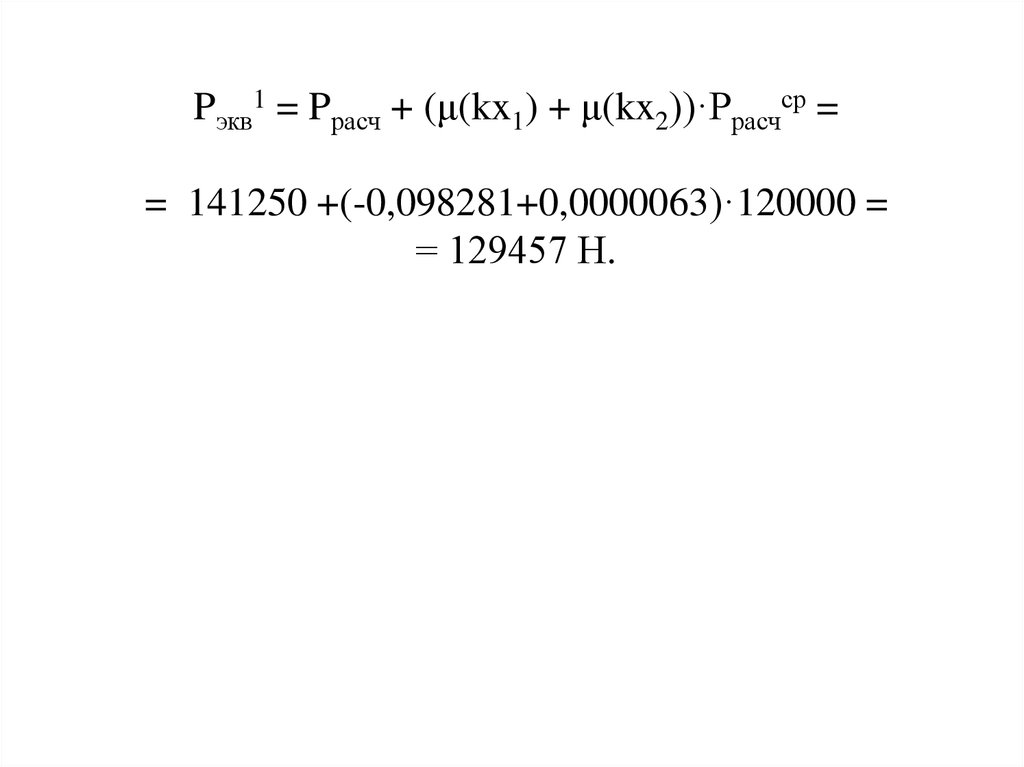

























 physics
physics industry
industry








