Площади геометрических фигур. Задачи

1.

Площадь прямоугольника
а
b
а

2.

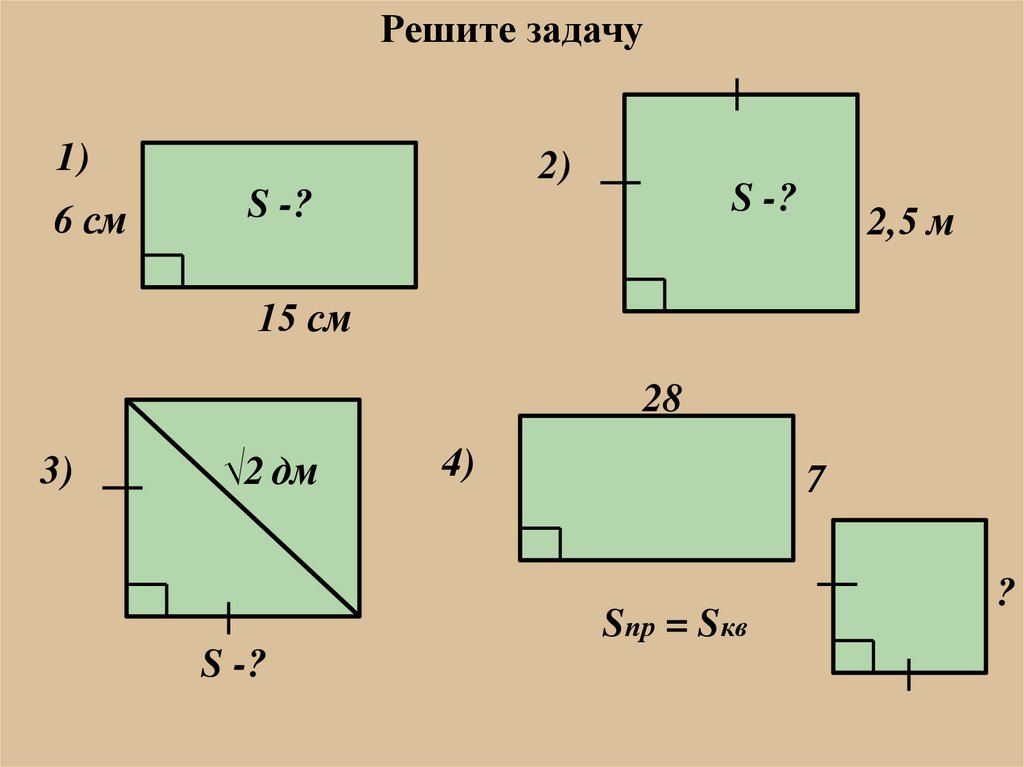
Решите задачу
1)
6 см
2)
S -?
S -?
2,5 м
15 см
28
3)
√2 дм
4)
7
Sпр = Sкв
S -?
?

3.

Площадь параллелограмма
a
h
α
a
d1
b
α
d2
d1
d2

4.

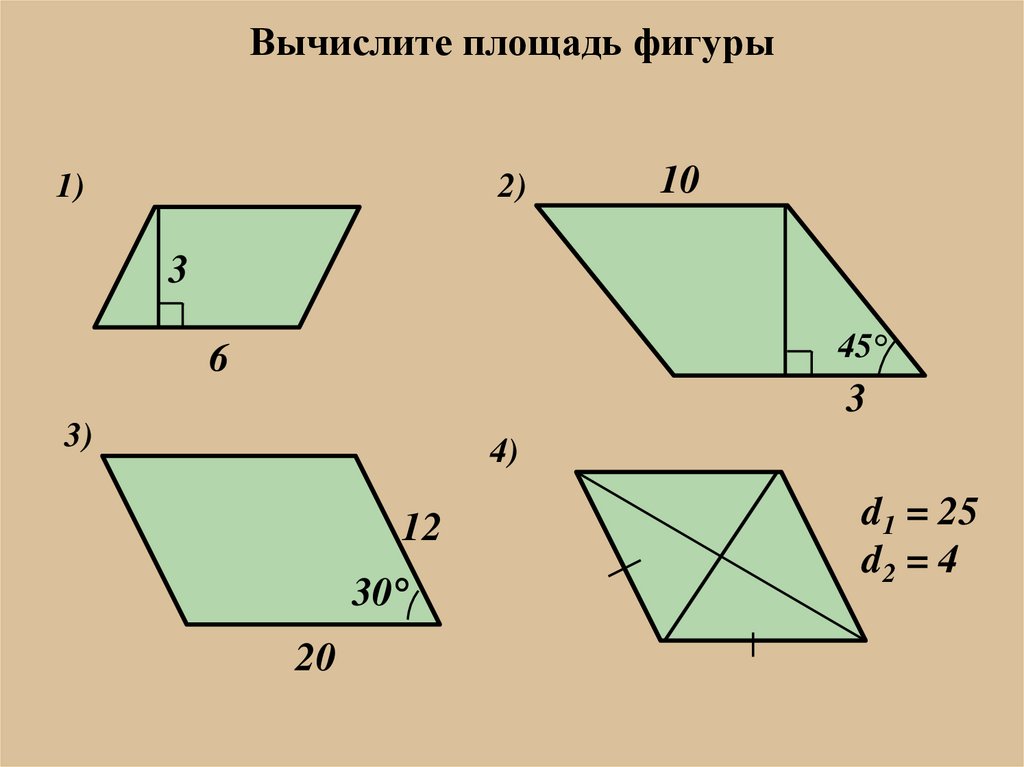
Вычислите площадь фигуры
1)
2)
10
3
45°
6
3
3)
4)
12
30°
20
d1 = 25
d2 = 4

5.

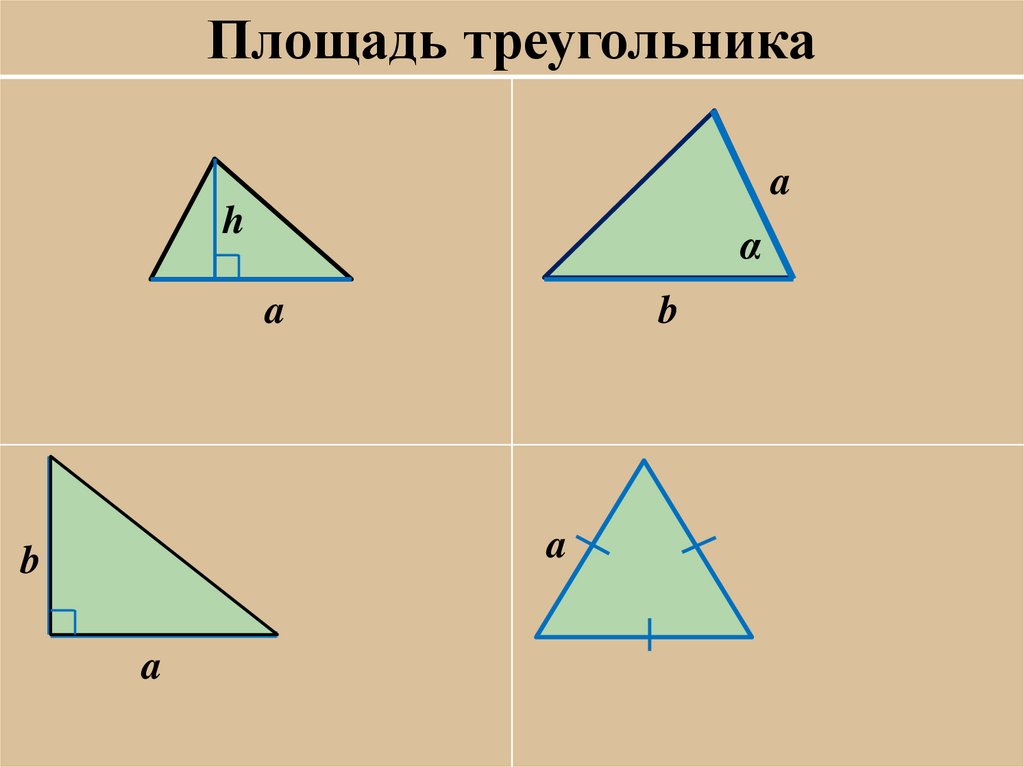
Площадь треугольника
a
h
α
a
b
a
b
a

6.

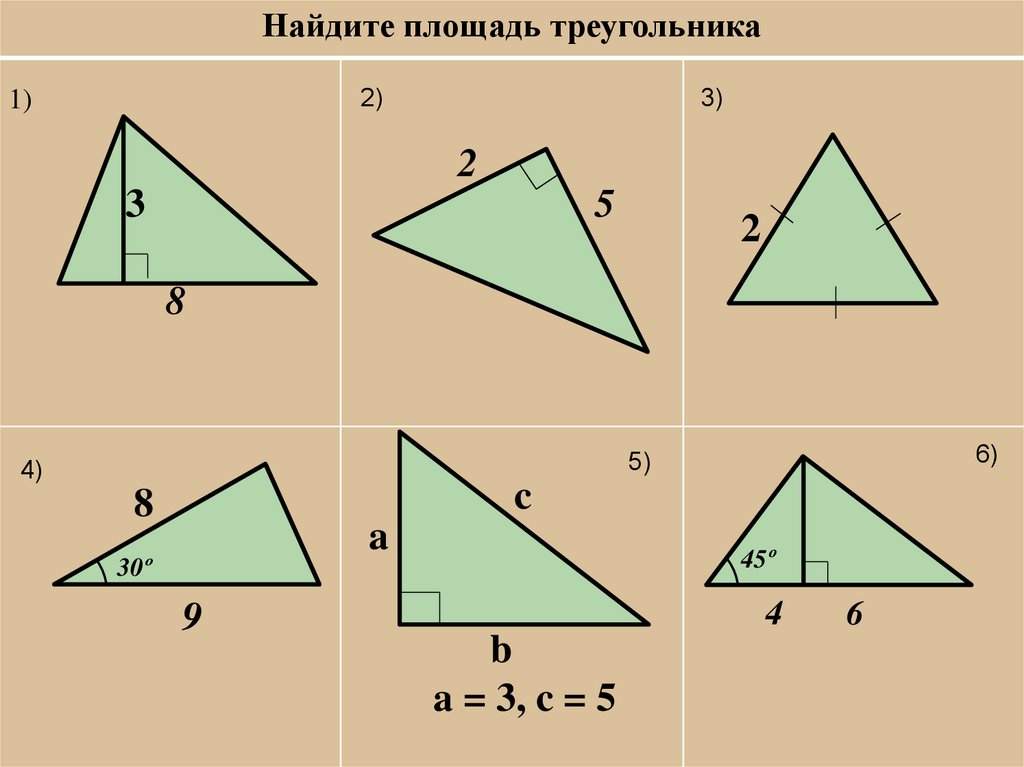
Найдите площадь треугольника
2)
1)
3)
2
3
5
2
8
6)
5)
4)
c
8
a
45º
30º
9
4
b
a = 3, c = 5
6

7.

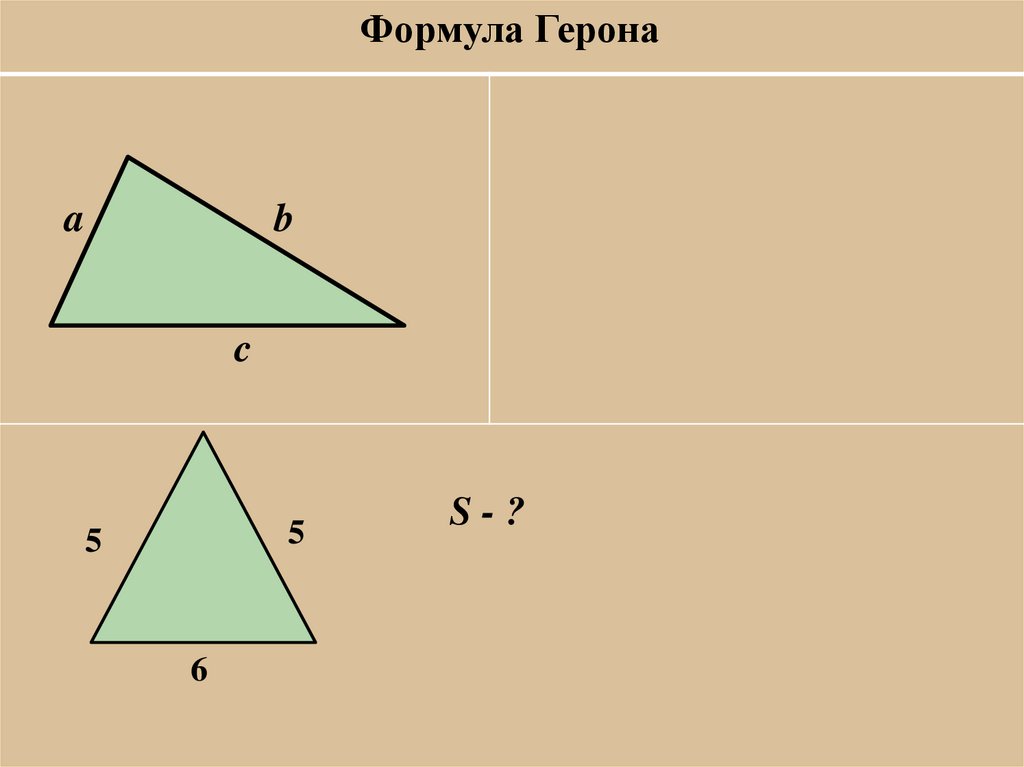
Формула Герона
a
b
c
5
5
6
S-?

8.

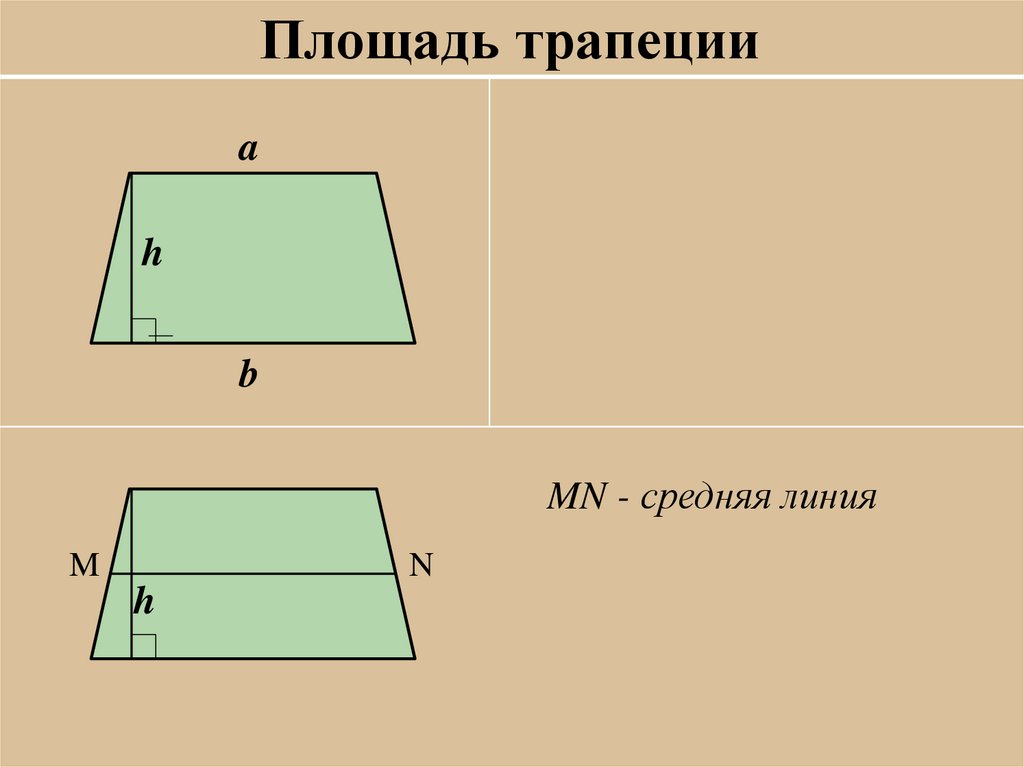
Площадь трапеции
a
h
b
MN - средняя линия
M
N
h

9.

Найдите площадь трапеции
1)
4)
2)
3)
5)
6)

10.

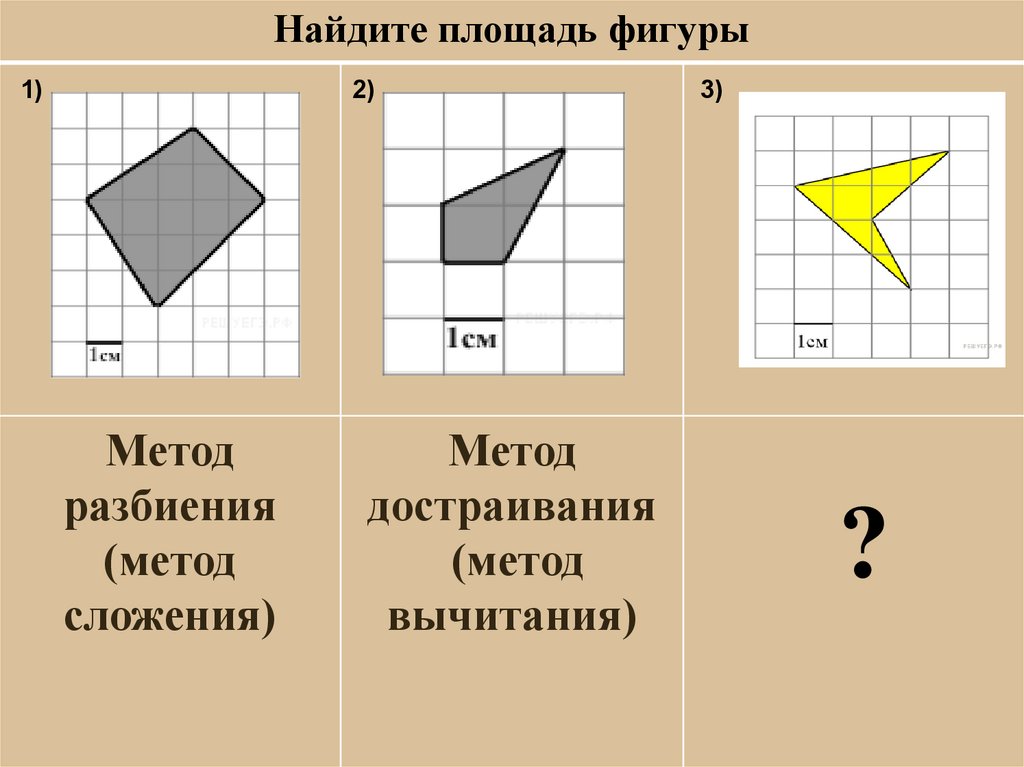
Найдите площадь фигуры
1)
2)
Метод
разбиения
(метод
сложения)
Метод
достраивания
(метод
вычитания)
3)
?

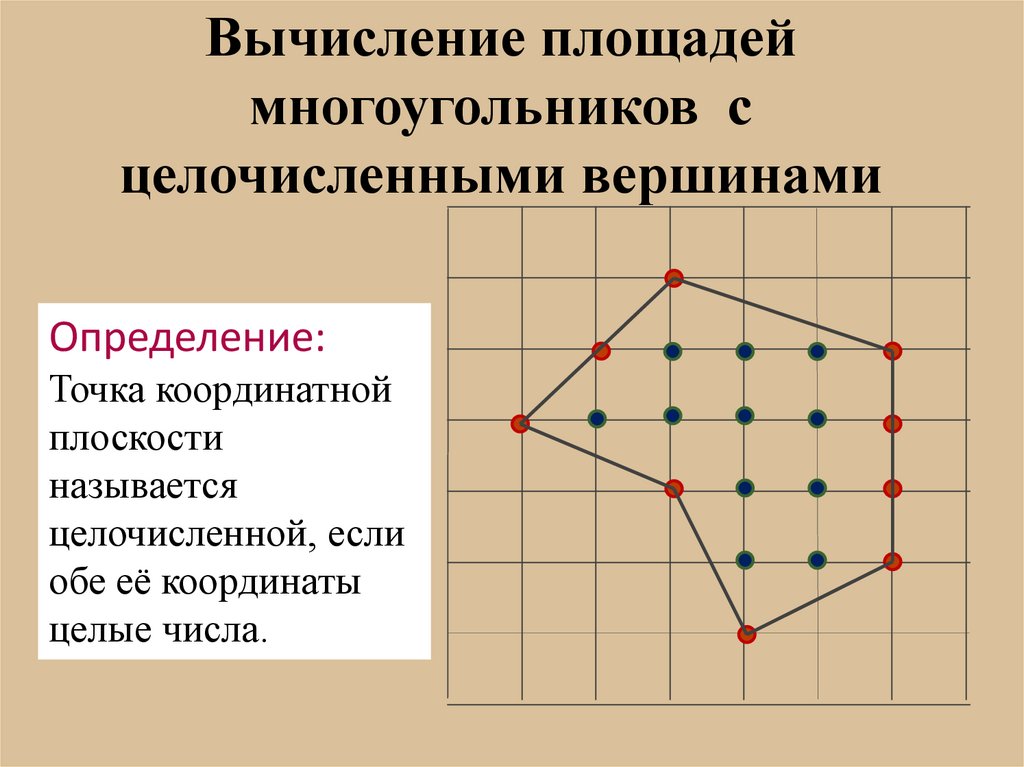
11. Вычисление площадей многоугольников с целочисленными вершинами

Определение:
Точка координатной
плоскости
называется
целочисленной, если
обе её координаты
целые числа.

12.

Площадь многоугольника с
целочисленными вершинами
Г
S В
1
2
(В — количество целочисленных точек внутри
многоугольника,
Г — количество целочисленных точек на границе
многоугольника)
Формула была открыта австрийским
математиком Георгом Пиком в 1899 г.

13.

Алгоритм применения формулы Пика:
Г
S В
1
2
1. Посчитать количество целочисленных точек,
лежащих внутри фигуры (В)
2. Посчитать количество целочисленных точек,
лежащих на границе фигуры (Г)
3. Подставить найденные значения в формулу
и посчитать площадь.