Similar presentations:
Постоянный ток. Закон Ома для однородного участка цепи
1.
Тема 2Постоянный ток
2. Закон Ома для однородного участка цепи
U IRI- ток ]А]=[Кл/c]
Георг Ом
1789 –1854
R- сопротивление, [Ом]=[В/А]
l
R
S
l- длина подводника,
S- площадь сечения
ρ – удельное сопротивление [Ом*м]
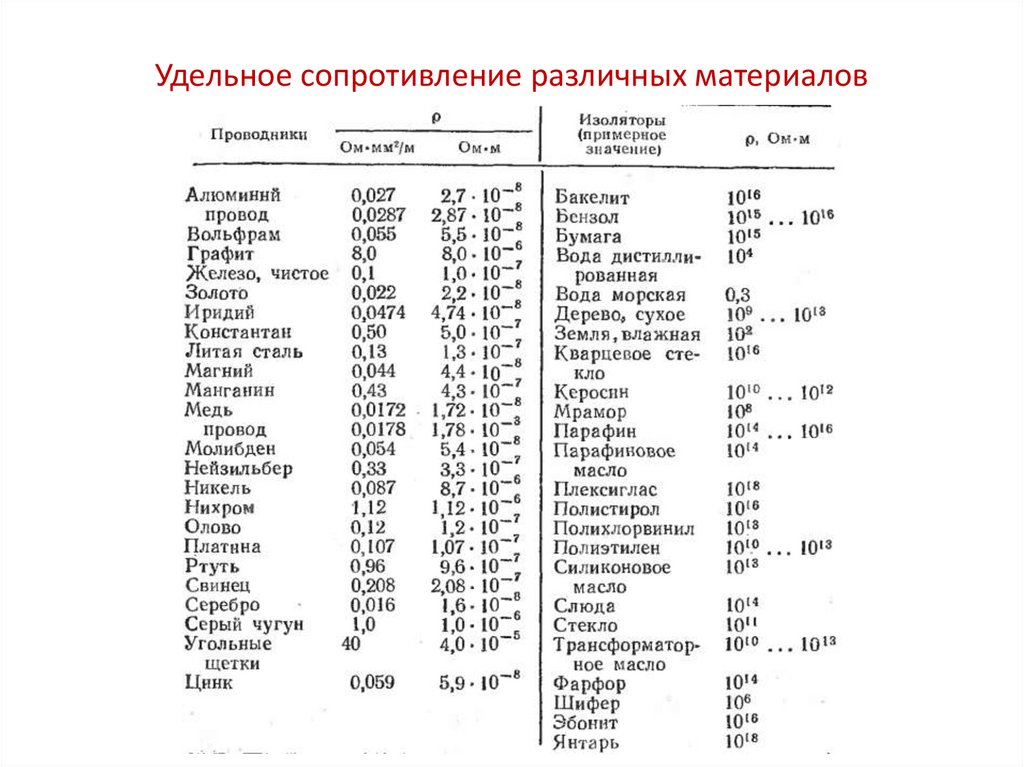
3. Удельное сопротивление различных материалов
4.
• Из закона Ома для участка проводника длинойdl:
U Edl EdS
I
R ρ dl
ρ
dS
dI
1
j
E
dS ρ
• можно записать
j σE
Закона Ома в дифференциальной форме
σ 1 / ρ – удельная электропроводность.
5. Дрейфовая скорость
• Плотность тока можно выразить через зарядэлектрона е, концентрацию зарядов n и
дрейфовую скорость u :
j enu
Для меди:
n
M Cu N A
Cu
8 1022 cm 3
При плотности тока 100A/cm2 :
j
мм
v
1
ne
с
6. Время релаксации объемных зарядов
- пусть объемная плотность заряда в проводящей средеdiv( j )
t
j E
-закон сохранения для заряда в дифференциальной
форме
- закон Ома
div( E )
t
0
0e
t / tr
divE
0
t
0
tr 0
-теорема Гаусса
Для морской воды:
0
tr
6*10 10 c
7. Выводы
Стационарных объёмных зарядов в однородной проводящей среде нет!8. Поверхностная плотность зарядов
Найти поверхностную плотность зарядов на границепроводников (пренебрегая контактной разностью потенциалов),
если через контакт течет ток j
E1
1
j - закон Ома в первой среде
2 0
E2 E0 E E0
2 0
E1 E0 E E0
E2
2
j - закон Ома во второй среде
- поле в первой среде
- поле во второй среде
E2 E1 j 2 j 1
j ( 2 1 ) 0
Поверхностная плотность заряда на границе сред
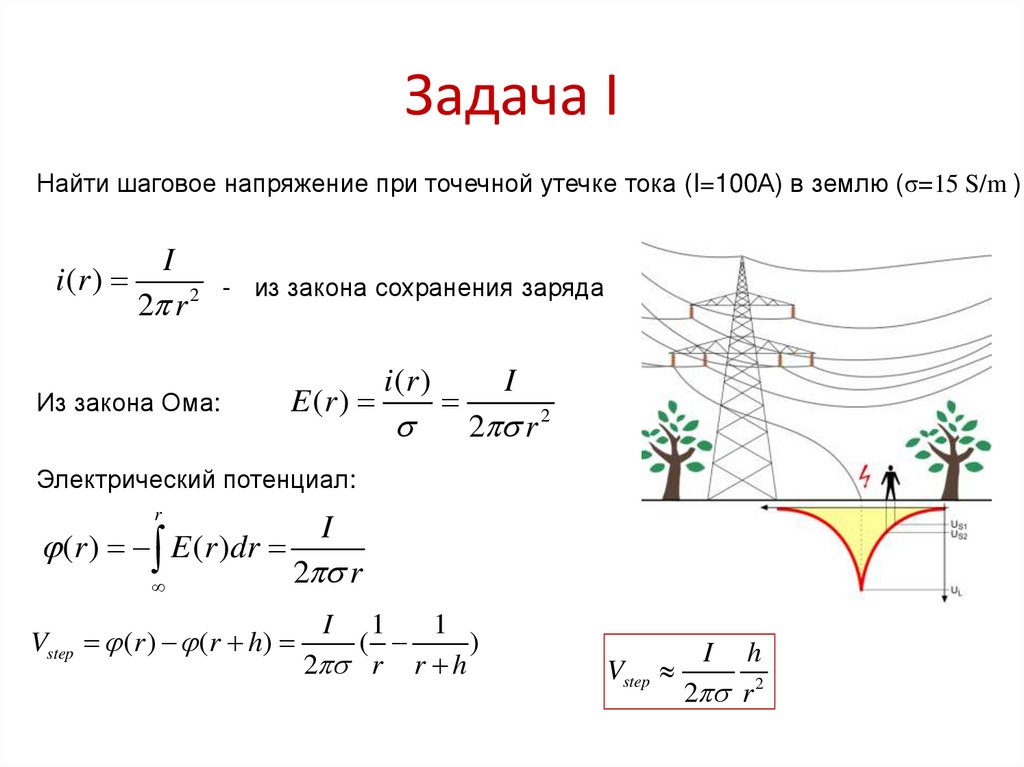
9. Задача I
Найти шаговое напряжение при точечной утечке тока (I=100А) в землю (σ=15 S/m )i (r )
I
2 r 2
- из закона сохранения заряда
Из закона Ома:
E (r )
i (r )
I
2 r 2
Электрический потенциал:
r
(r ) E (r )dr
I
2 r
Vstep (r ) (r h)
I
1
1
(
)
2 r r h
Vstep
I
h
2 r 2
10. Вопросы
Чем будет отличаться случай утечки тока при заданном напряжении?Что будет, если несколько проводов касаются земли?
По какому закону будет растекаться ток при утечке в тонкий пол?
11.
Измерение проводимости?l
1
A
R
l
I
A
12.
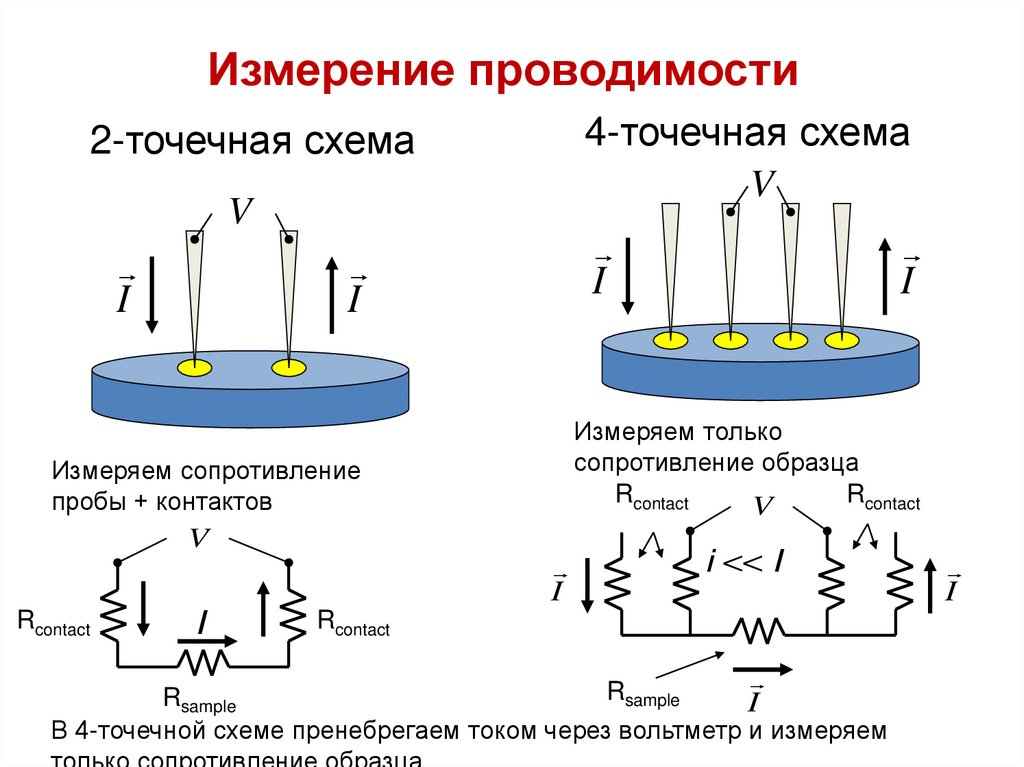
Измерение проводимости4-точечная схема
V
2-точечная схема
V
I
I
I
Измеряем только
сопротивление образца
Rcontact
Rcontact
V
Измеряем сопротивление
пробы + контактов
V
Rcontact
I
I
I
i << I
Rcontact
Rsample
Rsample
I
В 4-точечной схеме пренебрегаем током через вольтметр и измеряем
I
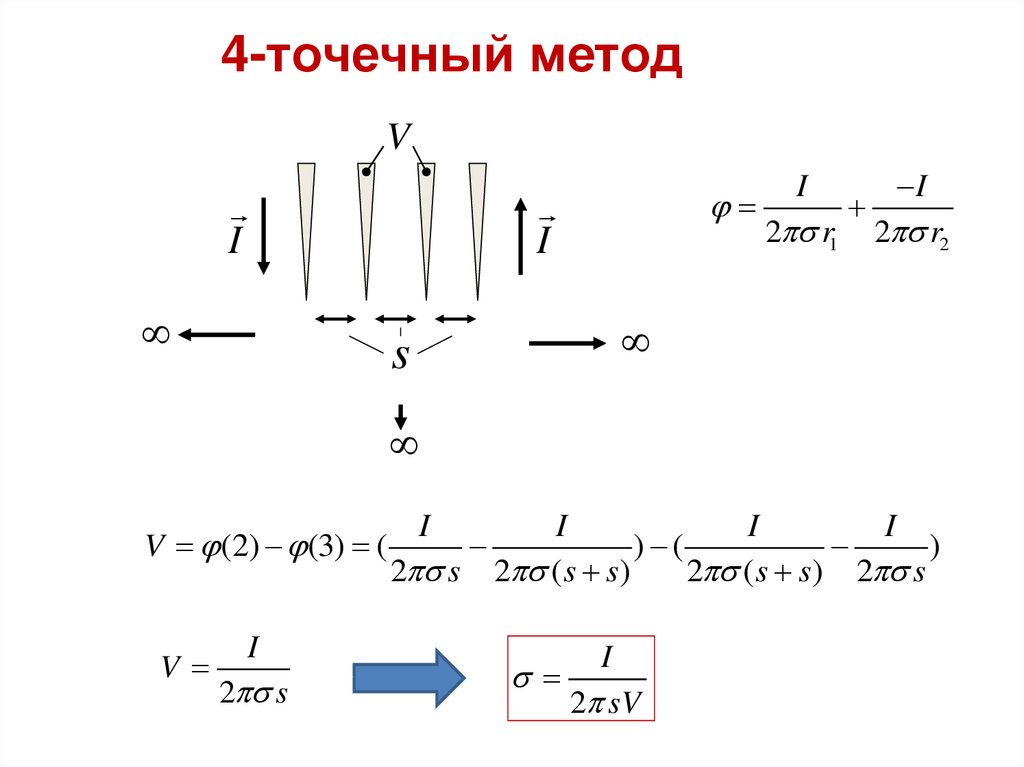
13.
4-точечный методV
I
I
I
2 r1
I
2 r2
s
V (2) (3) (
V
I
2 s
I
2 s
I
I
I
) (
)
2 ( s s)
2 ( s s) 2 s
I
2 sV
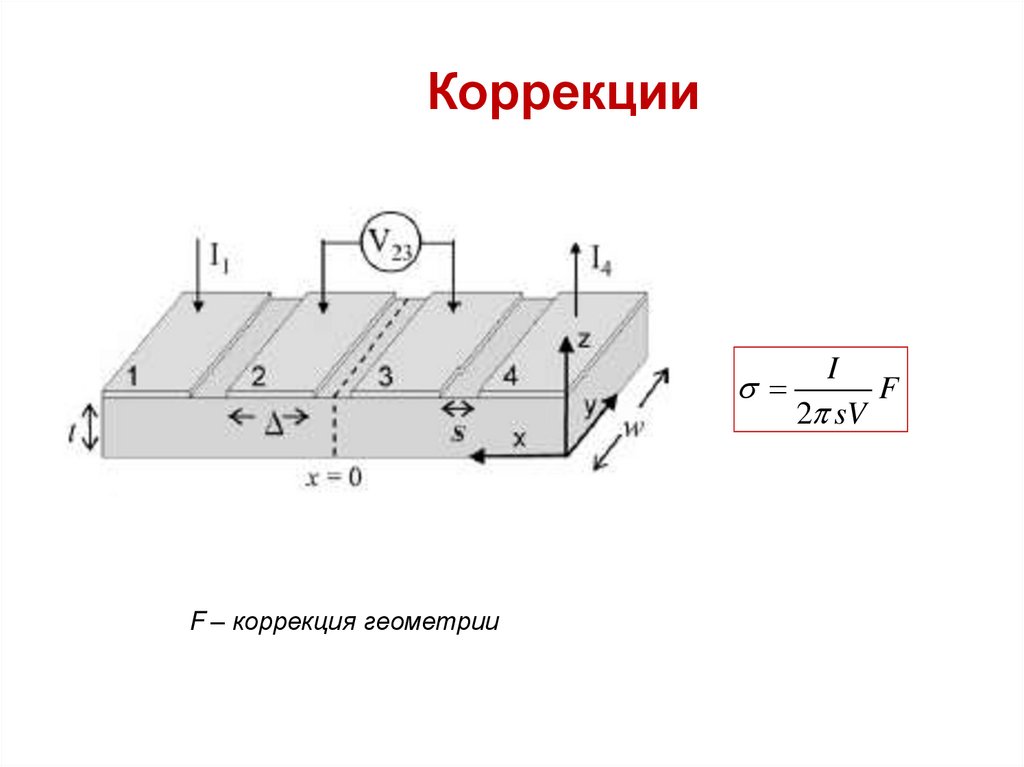
14.
КоррекцииI
F
2 sV
F – коррекция геометрии
15. Классическая задача
Найти сопротивление между соседними точками бесконечной квадратной сеткирезисторов:
Rgrid
R
2
16. Работа и мощность тока. Закон Джоуля
• Рассмотрим произвольный участок цепи, кконцам которого приложено напряжение U. За
время dt
dq Idt.
• силы электрического поля, действующего на
данном участке, совершают работу:
dA Udq UIdt.
• Общая работа:
A IUt
17.
Разделив работу на время, получим выражение длямощности:
dA
P
UI .
dt
Другие формулы для мощности и работы:
P RI ,
2
2
U
P
,
R
A RI t ,
2
2
U t
A
.
R
18.
James Prescott Joule1818-1889
William Thomson, 1st Baron Kelvin
1824-1907
John Dalton; 1766 —1844
19.
При протекании тока, в проводникевыделяется количество теплоты:
dQ RI dt.
2
Если ток изменяется со временем:
2
Q RI dt
2
1
Закон Джоуля в интегральной форме.
20.
• Тепловая мощность тока в элементе проводникаΔl, сечением ΔS, объемом
равна:
ΔV Δl ΔS
2
ΔW I R IΔφ jΔSEΔl j EΔV
Удельная мощность тока:
W
( jE)
V
21.
Согласно законуОма
в дифференциальной форме
получим j σE
Закон Джоуля в дифференциальной форме,
определяет плотность выделенной энергии:
E
j
2
2
22.
• Мощность, выделенная в единице объема2
проводника .
j
• Приведенная формула справедлива для
однородного участка цепи и для
неоднородного.
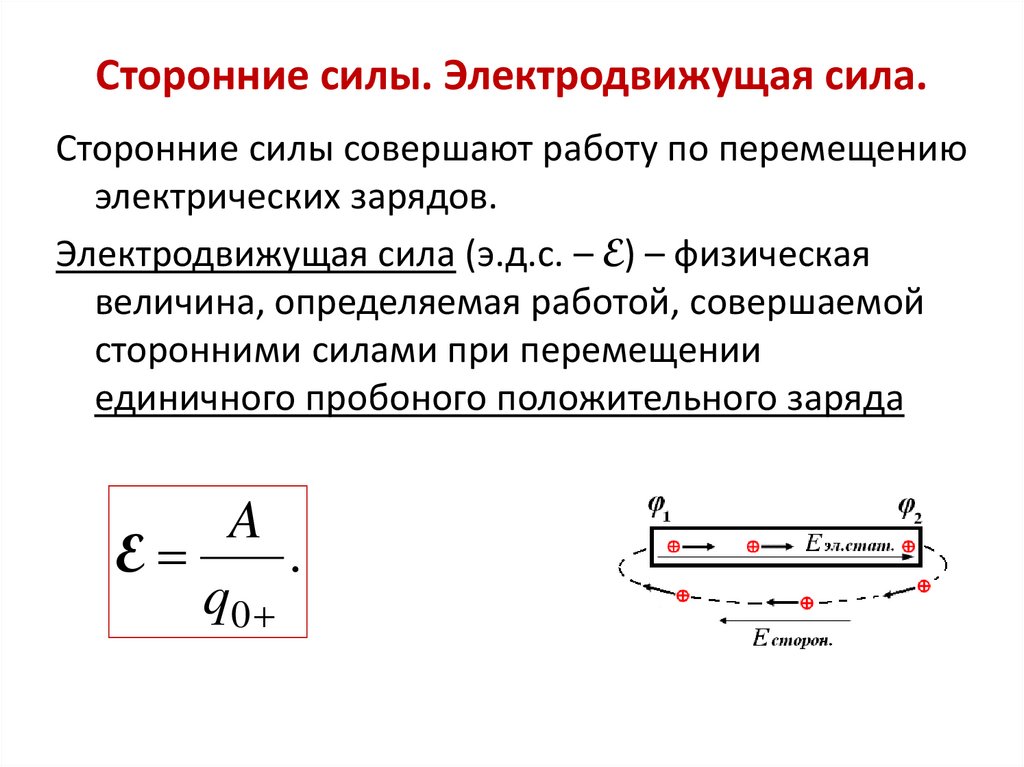
23. Сторонние силы. Электродвижущая сила.
Сторонние силы совершают работу по перемещениюэлектрических зарядов.
Электродвижущая сила (э.д.с. – E) – физическая
величина, определяемая работой, совершаемой
сторонними силами при перемещении
единичного пробоного положительного заряда
A
E
.
q0
24. Напряжение на участке цепи
Напряжение - величина, численно равнаяработе, совершаемой полем
электростатических и сторонних сил при
перемещении единичного положительного
заряда на этом участке цепи
U 1 2 E.
25. Закон Ома для неоднородного участка цепи
• Работа, совершаемая кулоновскими исторонними силами по перемещению
единичного положительного заряда q0+ –
падение напряжения (напряжение).
I
1 2 E
R
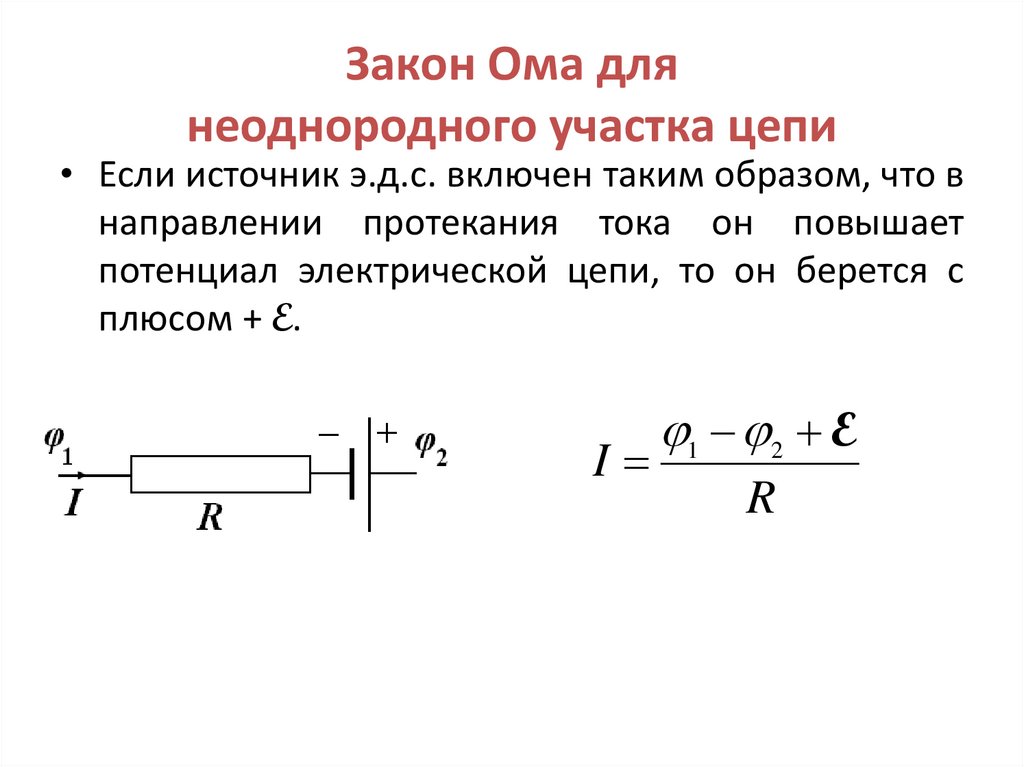
26. Закон Ома для неоднородного участка цепи
• Если источник э.д.с. включен таким образом, что внаправлении протекания тока он повышает
потенциал электрической цепи, то он берется с
плюсом + E.
I
1 2 E
R
27. Закон Ома для замкнутой цепи
• Если цепь замкнутая, то φ1 = φ2.E
I
;
Rполн
Rполн rвнутр.ист.т. Rвнеш.цепи .
28.
КПД источника тока•Рассмотрим элементарную электрическую
цепь, содержащую источник ЭДС с
внутренним сопротивлением r, и внешним
сопротивлением R
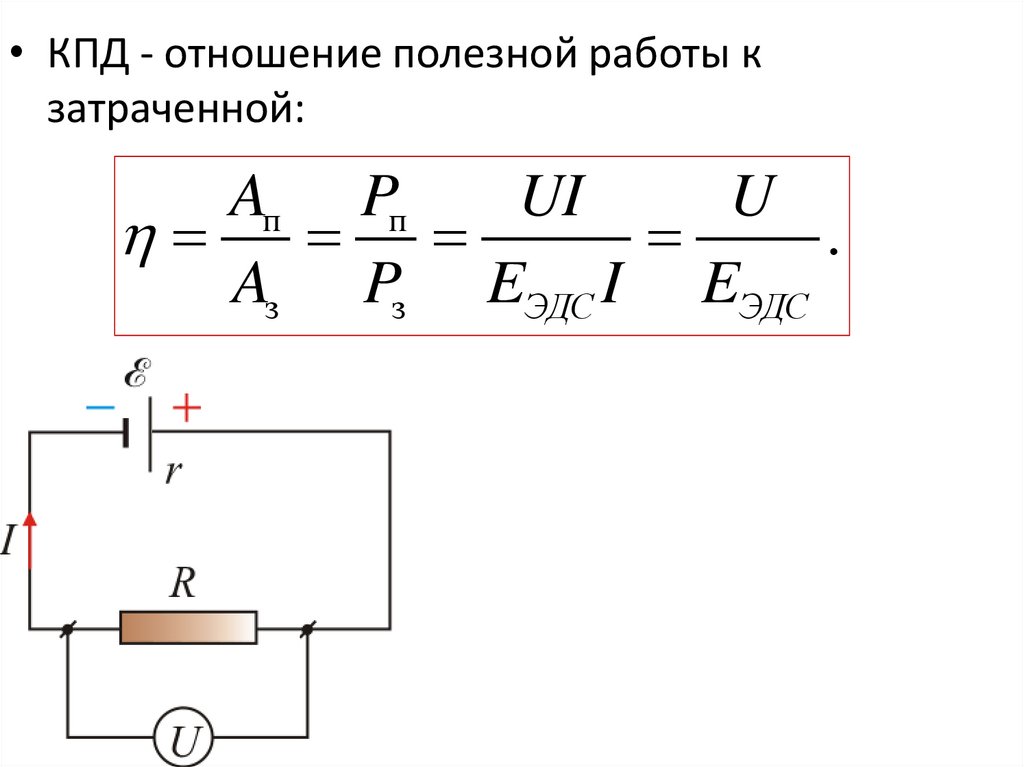
29.
• КПД - отношение полезной работы кзатраченной:
Aп Pп
UI
U
.
Aз Pз EЭДС I EЭДС
30.
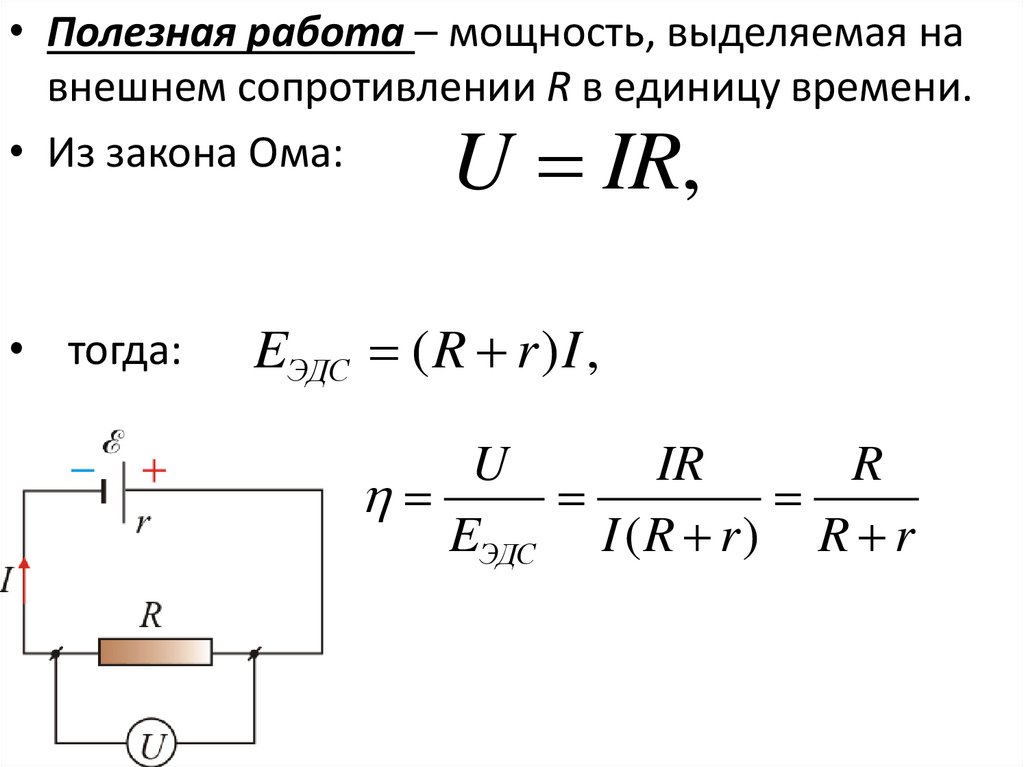
• Полезная работа – мощность, выделяемая навнешнем сопротивлении R в единицу времени.
• Из закона Ома:
U IR,
• тогда:
EЭДС ( R r ) I ,
U
IR
R
EЭДС I ( R r ) R r
31.
• Таким образом, имеем, что при R ,η 1,но при этом ток в цепи мал и полезная
мощность мала.
R
R r
•Условия, при которых полезная мощность
будет максимальна.
dPп
0.
dR
32.
2EЭДС
Pп I R
R
R r
2
EЭДС
dPп
dR
2
R r 2 r R EЭДС
4
R r
2
EЭДС R r 2 R 0
2
R r
dPп
0.
dR
2
R
0
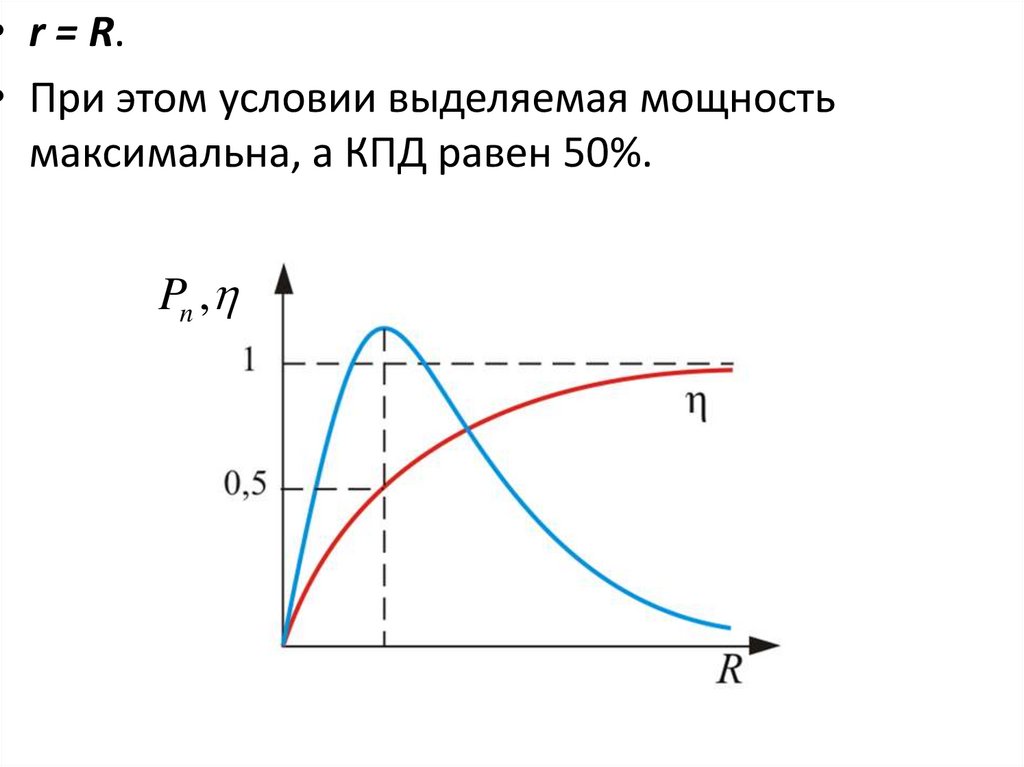
33.
• r = R.• При этом условии выделяемая мощность
максимальна, а КПД равен 50%.
Pn ,
34. Выводы
• Для каждого источника тока существует свояоптимальная полезная нагрузка
• И для каждой нагрузки надо подбирать свой
источник тока
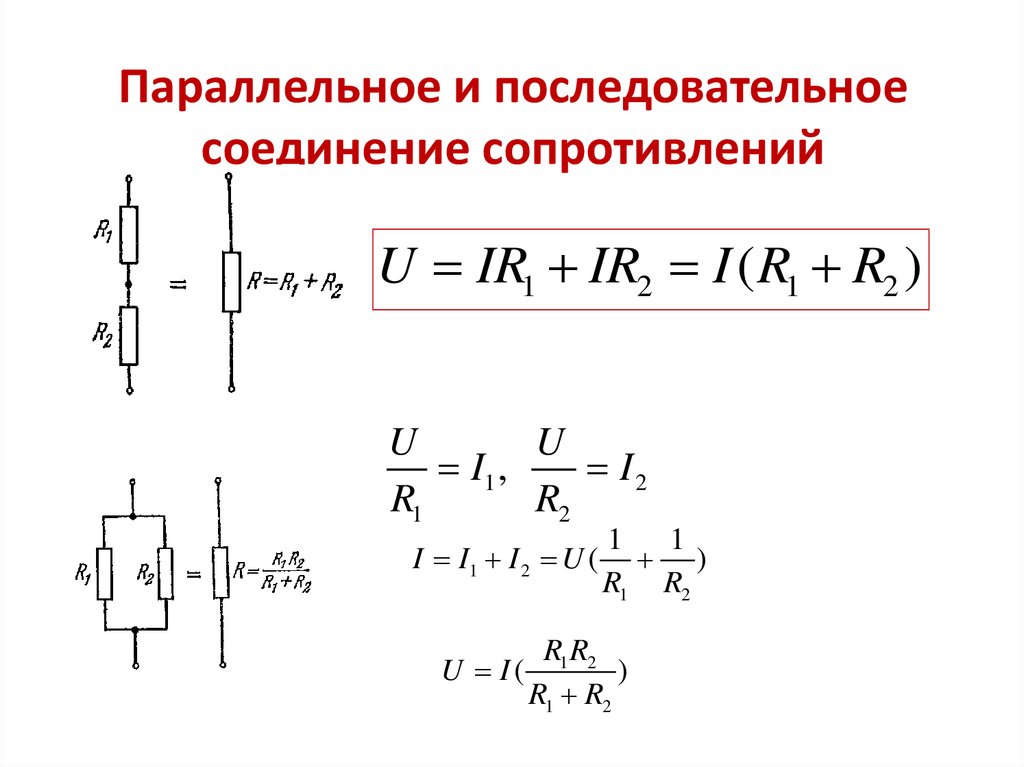
35. Параллельное и последовательное соединение сопротивлений
U IR1 IR2 I ( R1 R2 )U
U
I1 ,
I2
R1
R2
I I1 I 2 U (
1
1
)
R1 R2
R1 R2
U I(
)
R1 R2
36. Правила Кирхгофа для разветвленных цепей с переменным током
37.
Gustav Robert Kirchhoff; 1824- 188738.
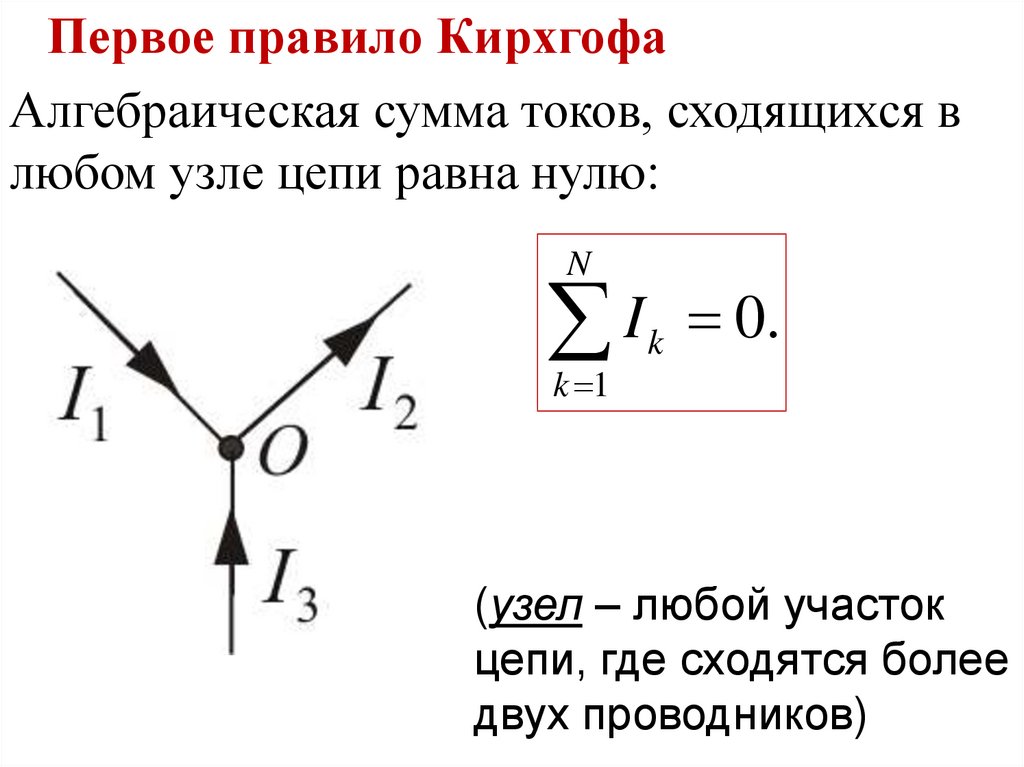
Первое правило КирхгофаАлгебраическая сумма токов, сходящихся в
любом узле цепи равна нулю:
N
I
k 1
k
0.
(узел – любой участок
цепи, где сходятся более
двух проводников)
39.
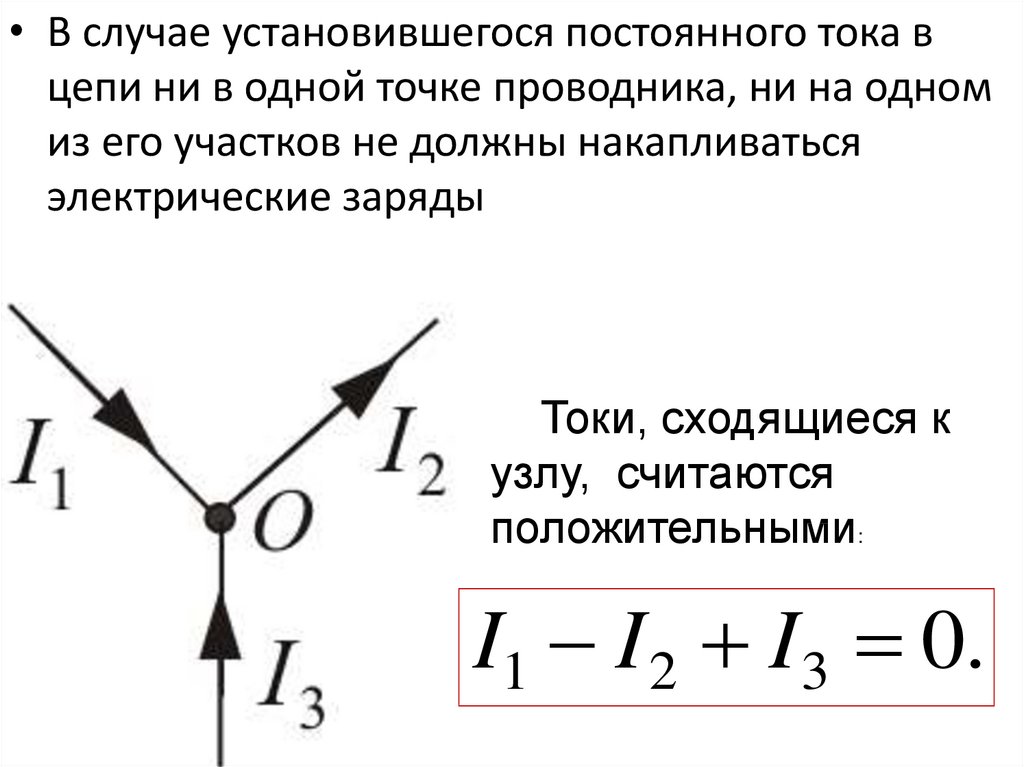
• В случае установившегося постоянного тока вцепи ни в одной точке проводника, ни на одном
из его участков не должны накапливаться
электрические заряды
Токи, сходящиеся к
узлу, считаются
положительными:
I1 I 2 I 3 0.
40.
• Второе правило Кирхгофа(обобщение закона Ома для
разветвленной цепи).
2 3 E1 I1 R1 ;
3 1 E 2 I 2 R2 ;
1 2 E 3 I 3 R3 .
Складывая получим:
I R E .
k k
k
k
k
41.
• В любом замкнутом контуре электрической цепиалгебраическая сумма произведения тока на
сопротивление равна алгебраической сумме
ЭДС, действующих в этом же контуре.
I R E .
k k
k
k
k
• Обход контуров осуществляется по часовой
стрелке, если направление обхода совпадает с
направлением тока, то ток берется со знаком
«плюс».
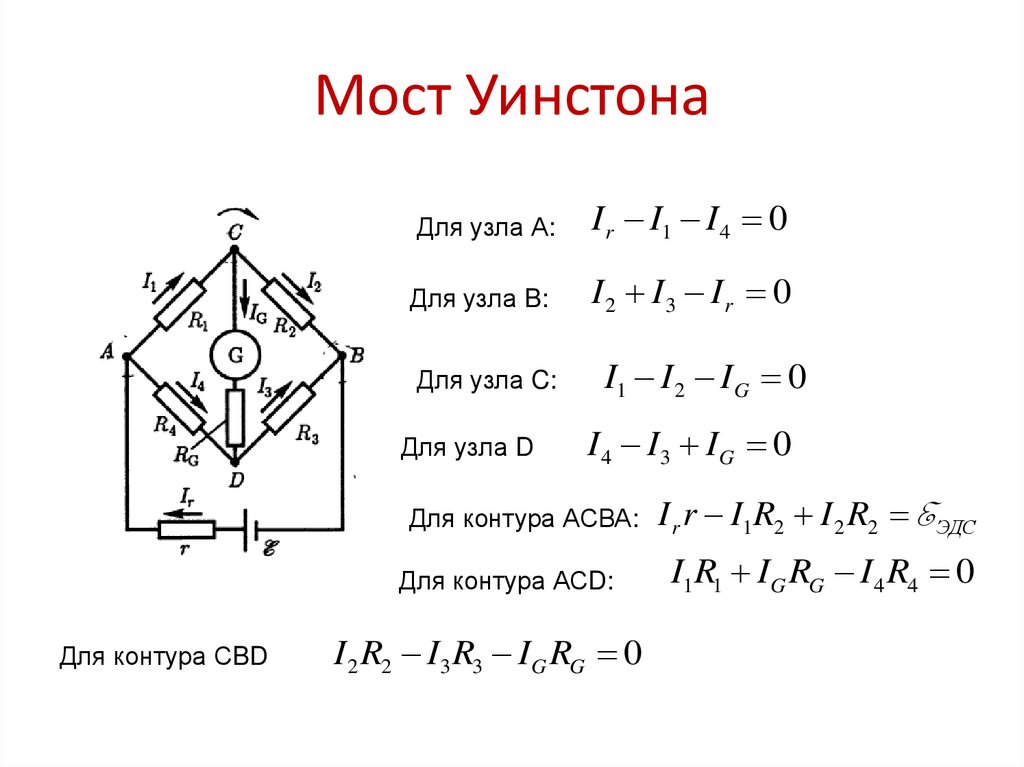
42. Мост Уинстона
Для узла А:I r I1 I 4 0
Для узла B:
I 2 I3 I r 0
Для узла C:
Для узла D
I1 I 2 IG 0
I 4 I3 IG 0
Для контура АСВА:
Для контура АСD:
Для контура СBD
I 2 R2 I3 R3 I G RG 0
I r r I1 R2 I 2 R2 E ЭДС
I1R1 IG RG I 4 R4 0
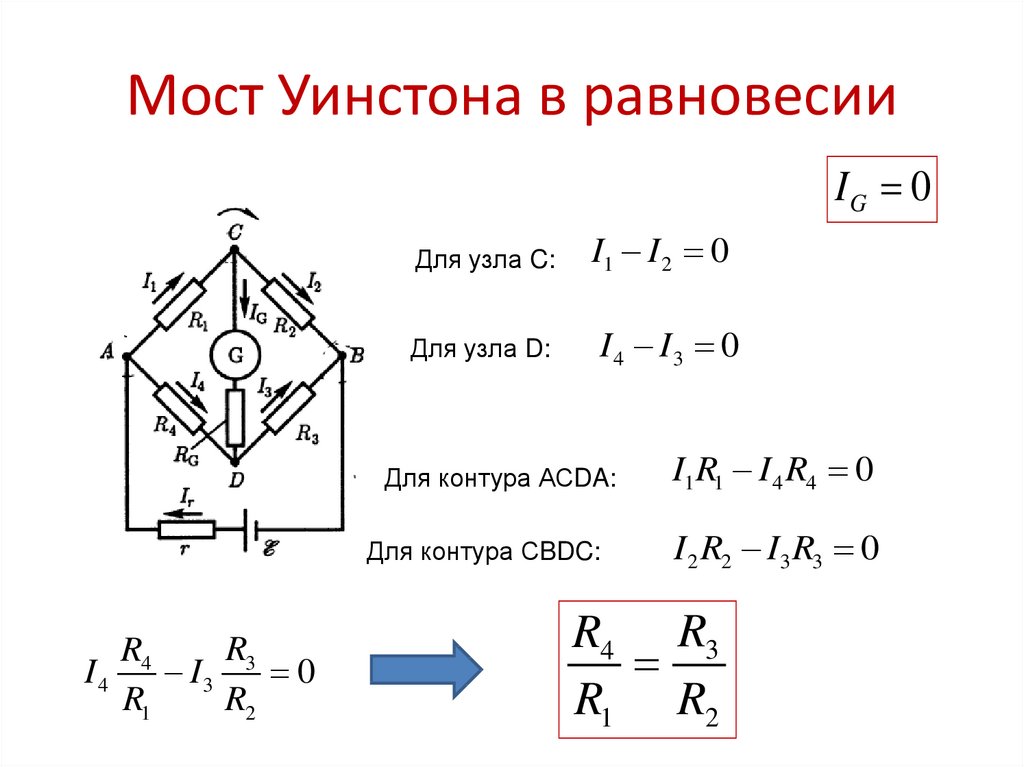
43. Мост Уинстона в равновесии
IG 0Для узла C:
Для узла D:
I1 I 2 0
I 4 I3 0
Для контура АСDA:
Для контура СBDC:
R3
R4
I4
I3
0
R1
R2
I1R1 I 4 R4 0
I 2 R2 I3 R3 0
R4 R3
R1 R2
44. Электрический ток, ионизации и рекомбинации в газах
Процесс ионизации заключается в том, что под действием
высокой температуры или излучения молекулы газа теряют
электроны и тем самым превращаются в положительные ионы.
Ток в газах – это встречный поток ионов и свободных
электронов.
Одновременно с процессом ионизации идёт обратный процесс
рекомбинации.
Рекомбинация – это нейтрализация при встрече разноименных
ионов или воссоединение иона и электрона в нейтральную
молекулу (атом).
45. Обозначения
• n – концентрация ионов• ∆ni – число пар ионов возникающих под действием
ионизатора за 1 сек в единице V
• ∆nr – число пар ионов рекомбинирующих за 1 сек в
единице объема
• ∆nj – число пар ионов уходящих из газоразрядного
промежутка к электродам за 1 сек
• j – плотность тока
• E – напряженность электрического поля
46.
Равновесное состояние, при котором число парионов, возникающих под действием ионизатора за
одну секунду в единице объёма, равно числу пар
рекомбинировавших и покинувших объем ионов.
Δni Δnr Δn j .
47.
Условие равновесия в случае слабого поляΔni Δnr Δn j .
Δn j Δnr .
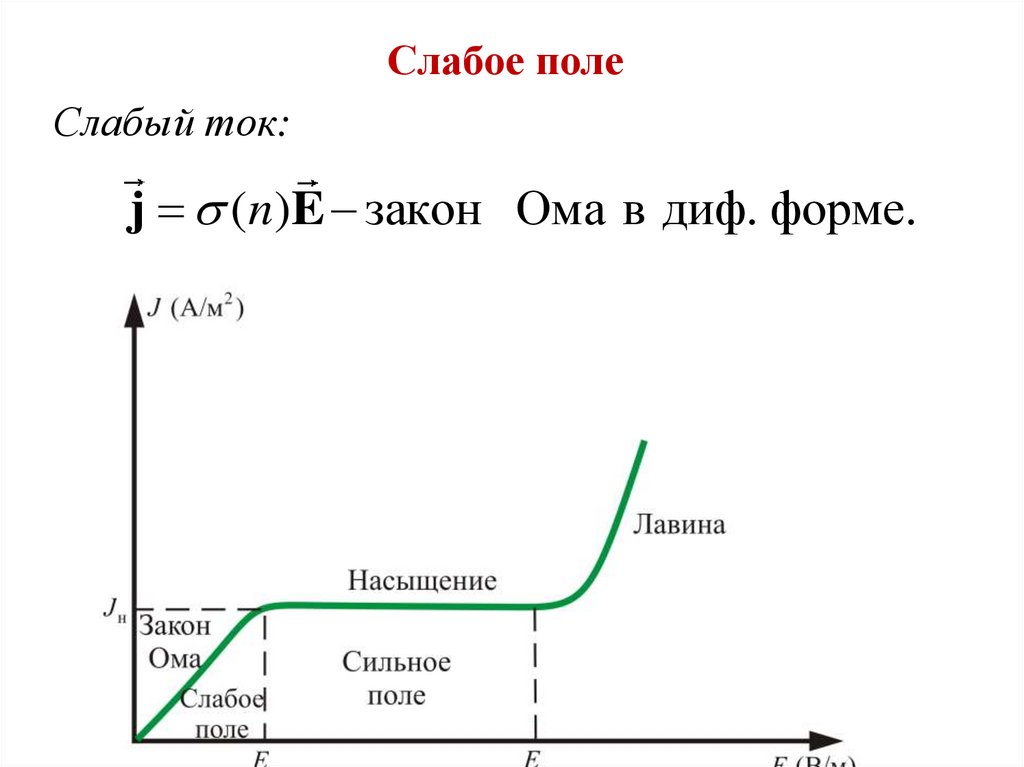
48.
Слабое полеСлабый ток:
j (n)E закон Ома в диф. форме.
49.
Сильное поле∆nr << ∆nj
∆ni = ∆nj
(∆nr→0)
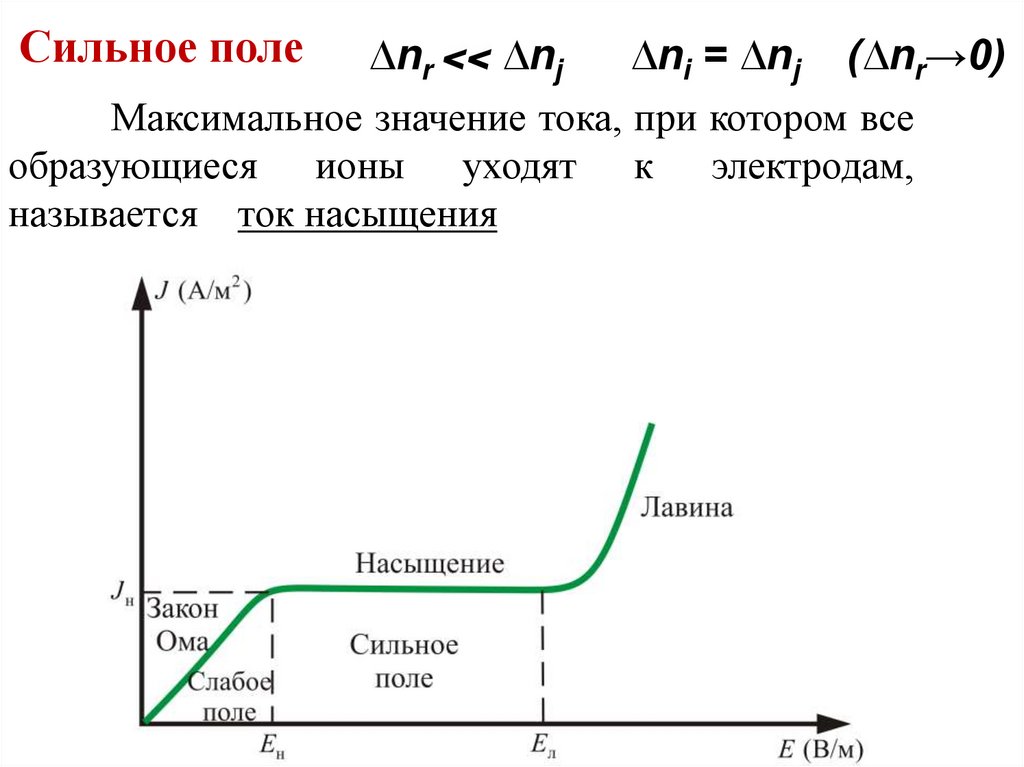
50.
Сильное поле∆nr << ∆nj
∆ni = ∆nj
(∆nr→0)
Максимальное значение тока, при котором все
образующиеся ионы уходят к электродам,
называется ток насыщения
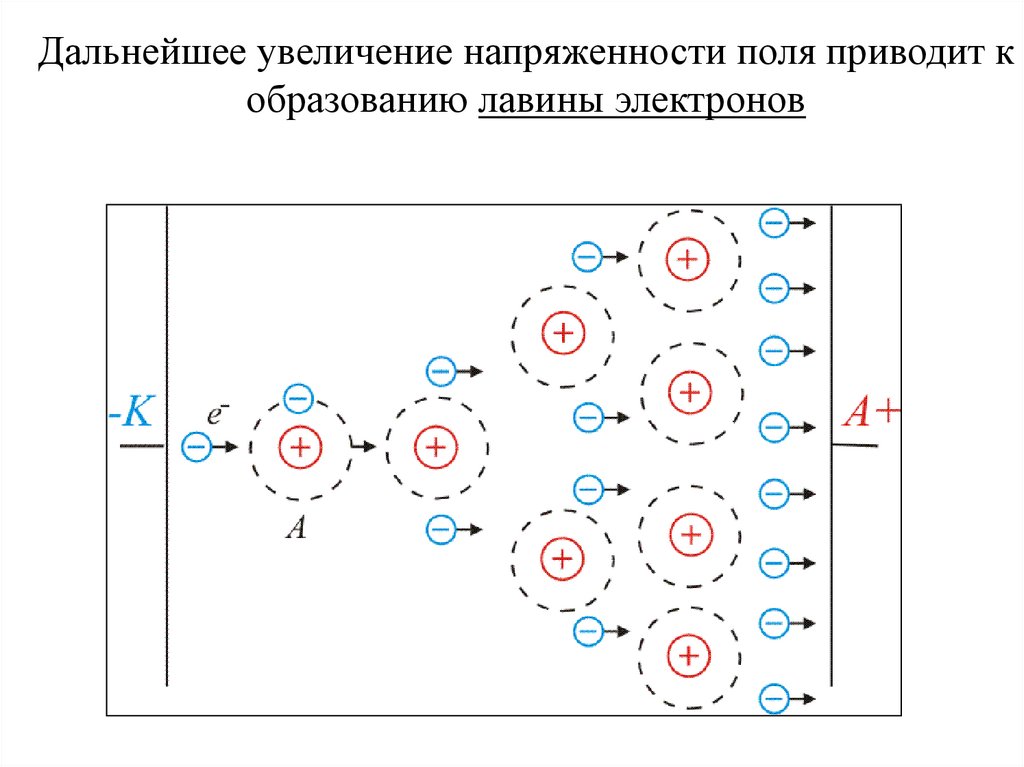
51.
Дальнейшее увеличение напряженности поля приводит кобразованию лавины электронов
52.
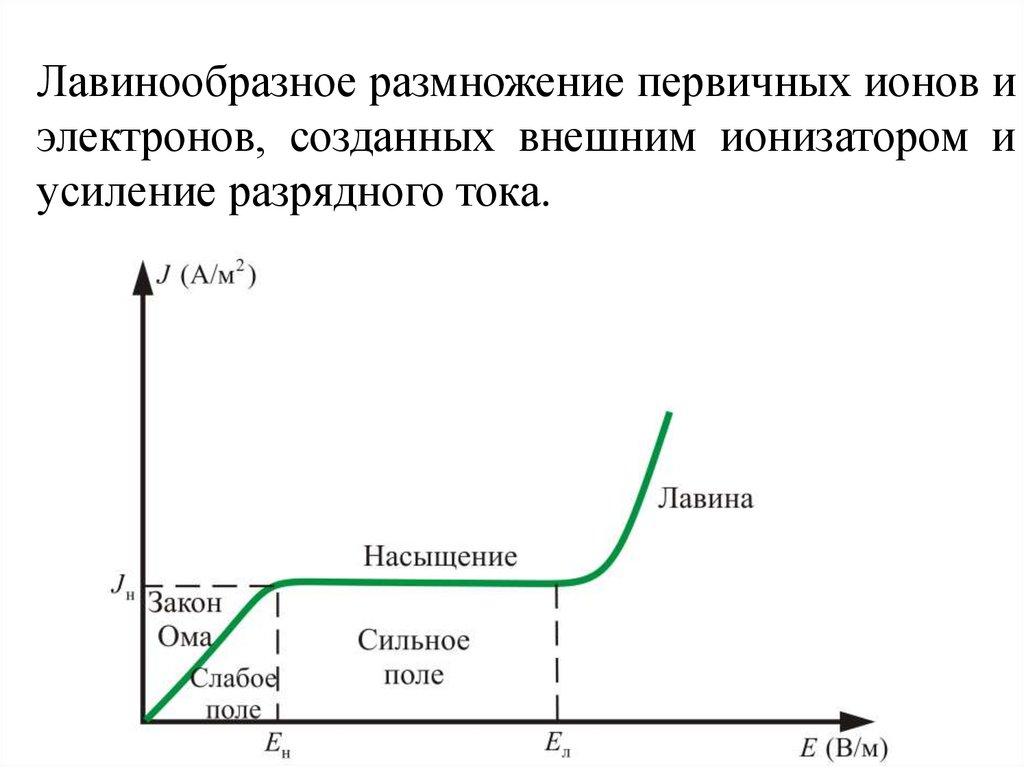
Лавинообразное размножение первичных ионов иэлектронов, созданных внешним ионизатором и
усиление разрядного тока.
53.
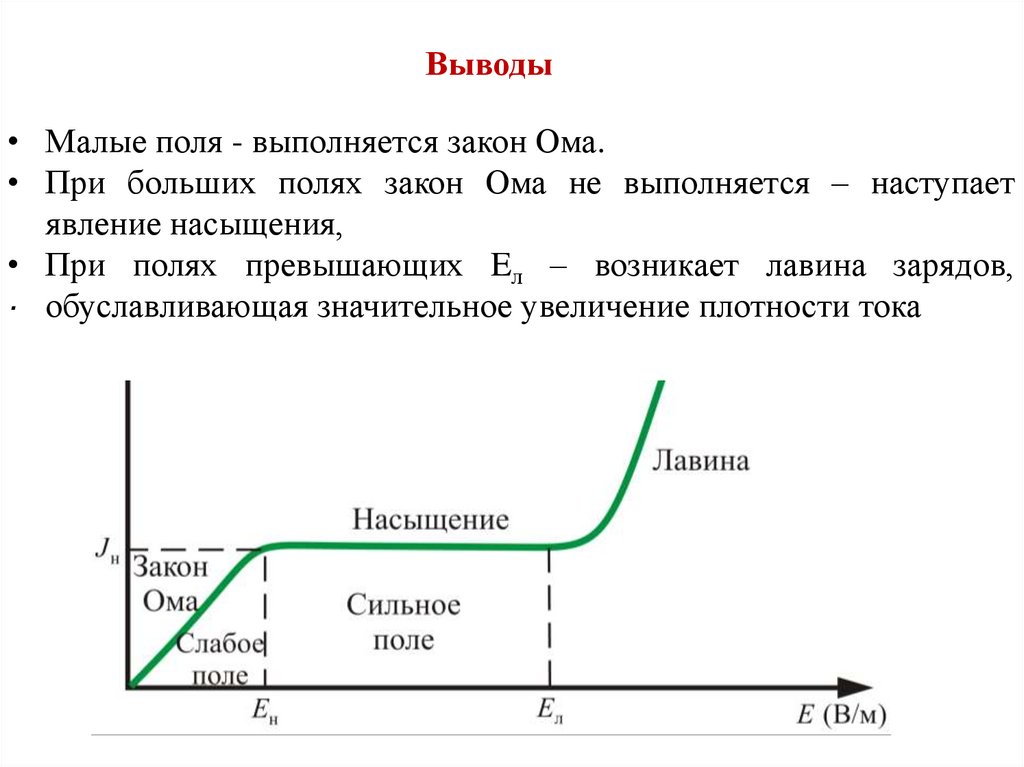
Выводы• Малые поля - выполняется закон Ома.
• При больших полях закон Ома не выполняется – наступает
явление насыщения,
• При полях превышающих Eл – возникает лавина зарядов,
. обуславливающая значительное увеличение плотности тока
54. Типы разрядов
В зависимости от давления газа,конфигурации электродов и параметров
внешней цепи существует четыре типа
самостоятельных разрядов:
• тлеющий разряд;
• искровой разряд;
• дуговой разряд;
• коронный разряд.
55. Тлеющий разряд
• Тлеющий разряд возникает при низкихдавлениях (в вакуумных трубках).
• Можно наблюдать в стеклянной трубке с
впаянными
у
концов
плоскими
металлическими электродами.
56. Тлеющий разряд
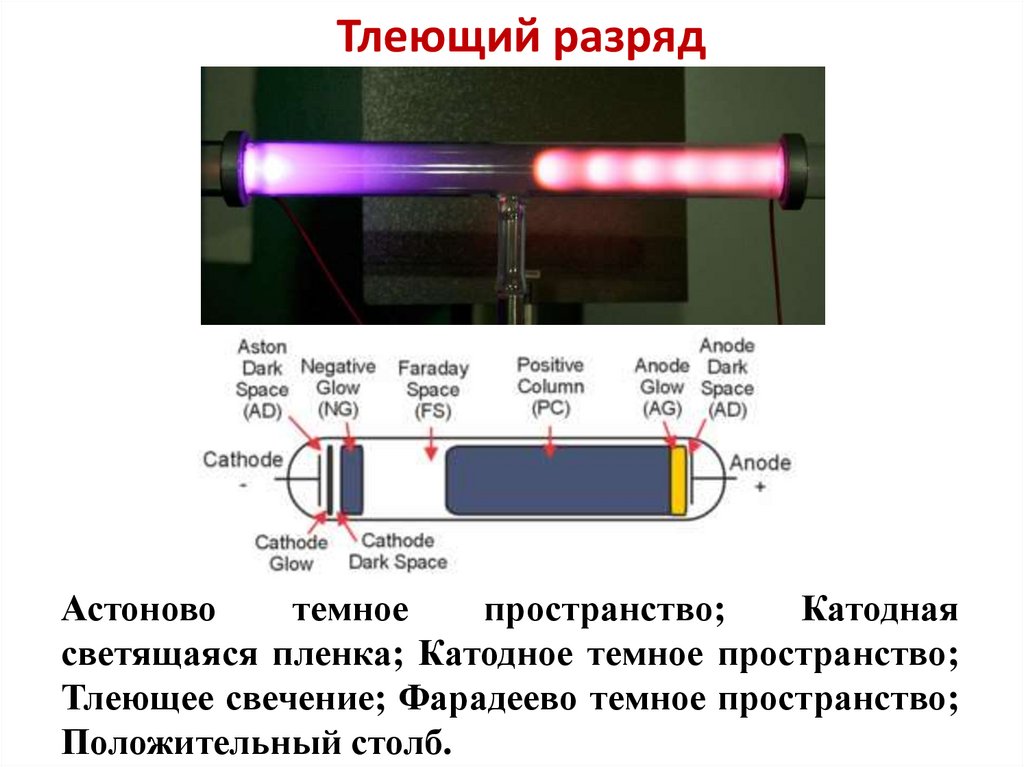
Астоновотемное
пространство;
Катодная
светящаяся пленка; Катодное темное пространство;
Тлеющее свечение; Фарадеево темное пространство;
Положительный столб.
57. Искровой разряд
• Искровой разряд возникает в газе обычно придавлениях порядка атмосферного Рат.
• Он характеризуется прерывистой формой.
• По внешнему виду искровой разряд представляет
собой
пучок
ярких
зигзагообразных
разветвляющихся тонких полос, мгновенно
пронизывающих разрядный промежуток, быстро
гаснущих и постоянно сменяющих друг друга.
• Эти полоски называют искровыми каналами.
58.
• В естественных природных условиях искровой разряднаблюдается в виде молнии.
•продолжительностью 0,2 ÷ 0,3с
• силой тока 104 – 105 А, длиной 20 км
59.
60.
61.
•Диаметр канала молнии• равен примерно 1 см,
•температура в канале молнии
•равна примерно 25 000°С,
•продолжительность разряда
•составляет доли секунды.
62.
63.
64. Дуговой разряд
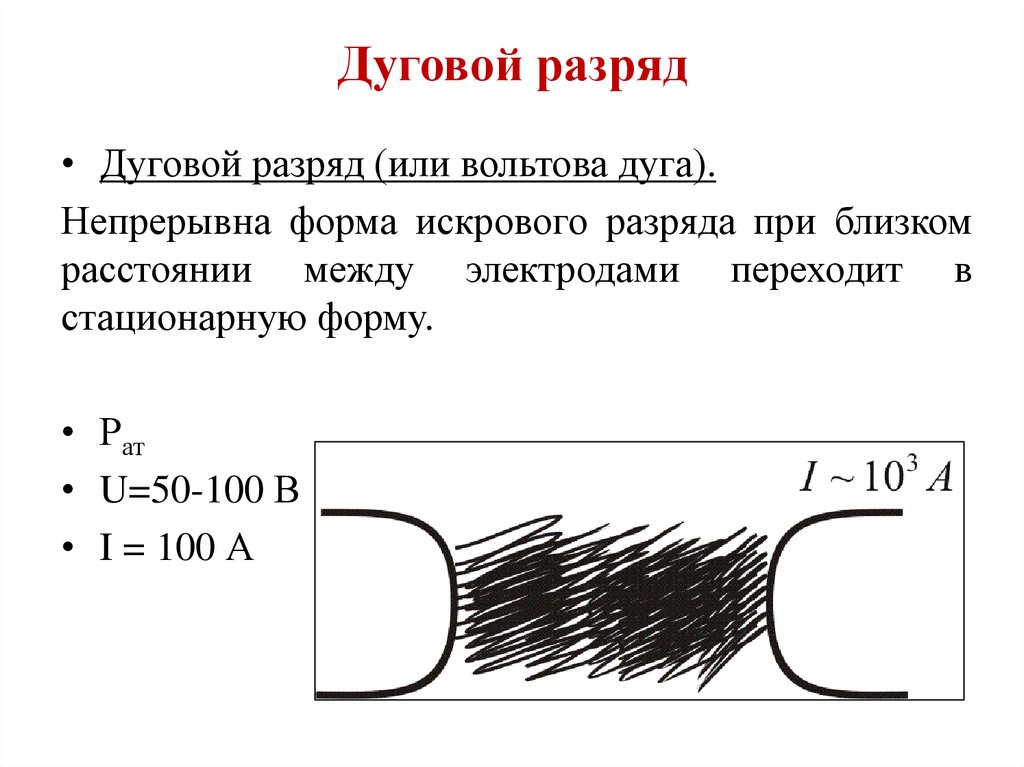
• Дуговой разряд (или вольтова дуга).Непрерывна форма искрового разряда при близком
расстоянии между электродами переходит в
стационарную форму.
• Рат
• U=50-100 В
• I = 100 А
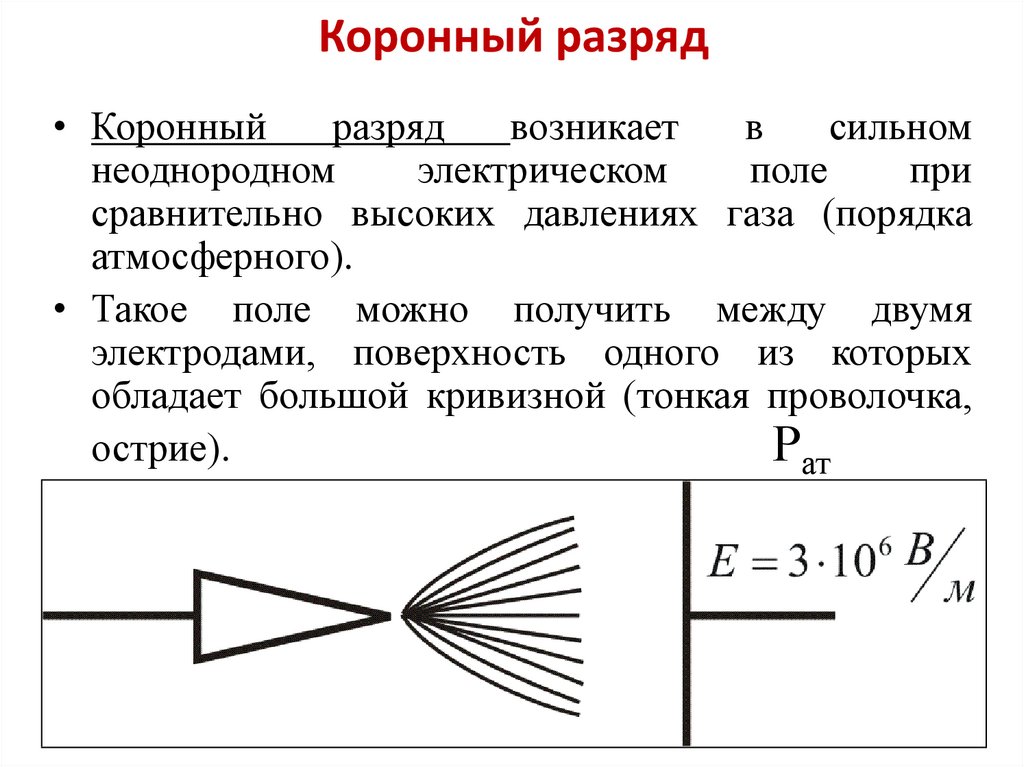
65. Коронный разряд
• Коронныйразряд
возникает
в
сильном
неоднородном
электрическом
поле
при
сравнительно высоких давлениях газа (порядка
атмосферного).
• Такое поле можно получить между двумя
электродами, поверхность одного из которых
обладает большой кривизной (тонкая проволочка,
острие).
Рат
66.
• Когда электрическое поле вблизи электрода сбольшой кривизной достигает примерно 3∙106 В/м,
вокруг него
возникает свечение, имеющее вид
оболочки или короны, откуда и произошло название
заряда.
67. Электростатические аналогии
Перенос заряда – дифференциальный законОма:
j grad
Диффузия– закон Фика:
J Dgrad n
Теплопроводность –закон Фурье:
q χ gradT
68. Электростатические аналогии
Задача: Найти потенциал заряженногошара (заряд Q) радиуса и заряда R:
Определение потенциала:
Теорема Гаусса:
E grad
4 r E
2
Q
0
Из определения потенциала:
Емкость:
Q
Edr
4 R 0
R
C 4 R 0
Q
E
4 r 2 0
69. Электростатические аналогии
Задача: Шар радиуса R в проводящей среде (проводимостьсреды - σ), через него идет полный ток I. Найти
потенциал шара.
Закон Ома:
j E
Закон сохранения заряда :
4 r j I
2
Из определения потенциала:
Сопротивление :
ROм
I
Edr
4 R
R
1
4 R
I
E
4 r 2
70. Электростатические аналогии
Задача: Шар радиуса R помещен в среду теплопроводности χс температурой Т0. Шар разогревается с мощностью W.
Найти установившуюся температуру шара.
Закон Фурье:
q gradT
Закон сохранение энергии:
Из закона Фурье:
W
q
4 r 2
4 r q W
2
1
W
T T0 qdr
R
4 R
Тепловое сопротивление (термин условный):
RHeat
1
4 R
71. Электростатические аналогии
Задача: Пусть в чистой воде медленно растворяется сахарныйшар радиуса R. Концентрация сахара на поверхности шара
сR. Найти полный молярный поток растворения шара
Закон Фика:
j D grad(c)
Закон сохранения вещества:
4 r j J
2
Из закона Фика:
1
J
cR jdr
DR
4 RD
Полный поток растворения :
J 4 RDcR
j
J
4 r 2
72. Электростатические аналогии. Выводы:
• Сходные уравнения в сходной геометрии - сходныерешения.
• Закон сохранения вещества для потоков, закон
сохранения зарядов для токов и теорема Гаусса это
аналогичные законы.
73. Магнитное поле
74. Изобретение Компаса
Han Dynasty (206 BC–220 AD)75.
76.
«О магните, магнитных телах и большом магните – Земле»William Gilbert 1544 -1603
77.
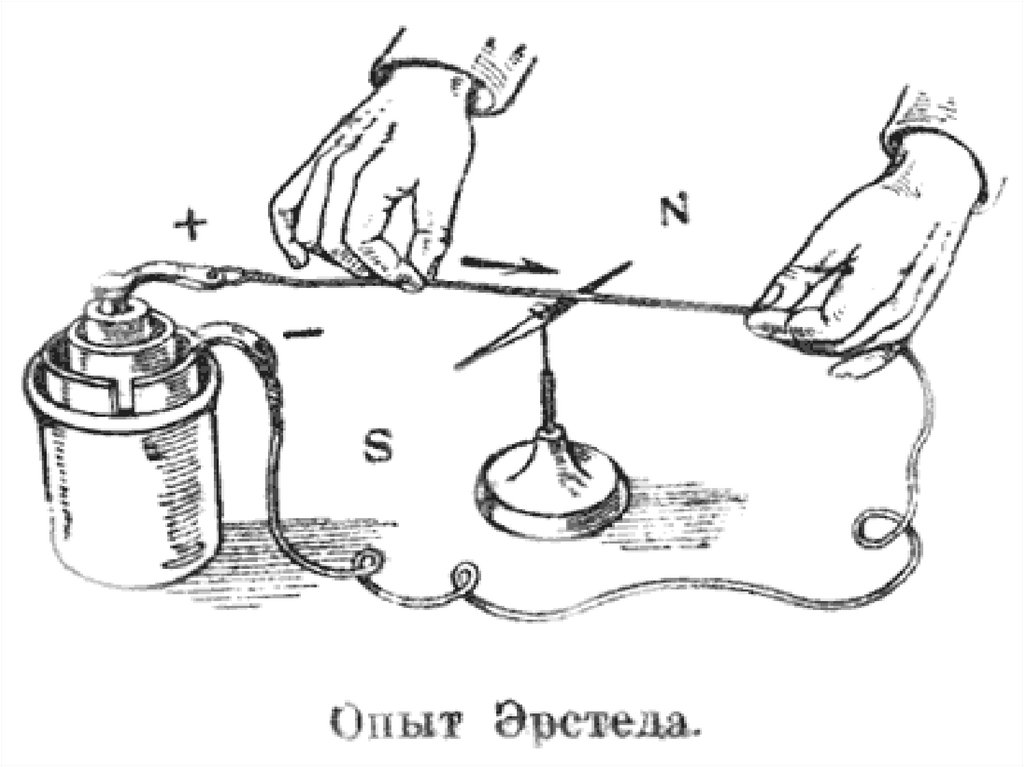
Hans Christian Ørsted,1777-1851André-Marie Ampère; 1775-1836
78.
79. Полная сила, действующая на заряд
F qE q[vB]Полная электромагнитная сила действующая на заряд – сила Лоренца
B
- Индукция магнитного поля [Тл]
Hendrik Antoon Lorentz;
1853-1928
80. Некоторые значения магнитной индукции
-5
Магнитное поле Земли в Европе – 2*10 Тл
-5
Магнитное поле Земли максимальное – 7*10 Тл
Магнитное поле стрелок компаса – 0,01 Тл
Магнитное поле подковообразного магнита – до 0,2 Тл
Магнитное поле солнечных пятен – 0,4 Тл
Магнитное поле ферромагнитного сердечника – до 1 Тл
Магнитное поле в ускорителе – до 10 Тл
Магнитное поле нейтронных звезд - 106 Тл
Магнитное поле звезд типа «Магнетар» - 1011 Тл
81. Свойства магнитного поля, действующего на заряды
F q[vB ]Сила пропорциональна скорости
Сила имеет релятивистскую природу
Не совершает работы
Направление определяется правилом
буравчика
82. Сила Ампера
F q[vB ]- сила, действующая на один заряд
F (n V )q[vB] - сила, действующая на объем проводника
j nqv
-плотность тока
F [ jB ] V
V LS
dF I [dlB]
- сила, действующая на объем проводника
- объем проводника
- Сила Ампера, действующая линейный проводник с током
83. Вопросы
1)Какая «противосила» у силы Лоренца?2)Совершает ли работу сила Ампера?
• За счет каких сил?
• За счет какой энергии?
84. Свойства силы Ампера
dF I [dlB]• Сила пропорциональна электрическому току
• Не зависит от природы и знаков зарядов,
движение которых образует ток
• Может совершать работу
• Направление определяется правилом
буравчика
• Является следствием силы Лоренца
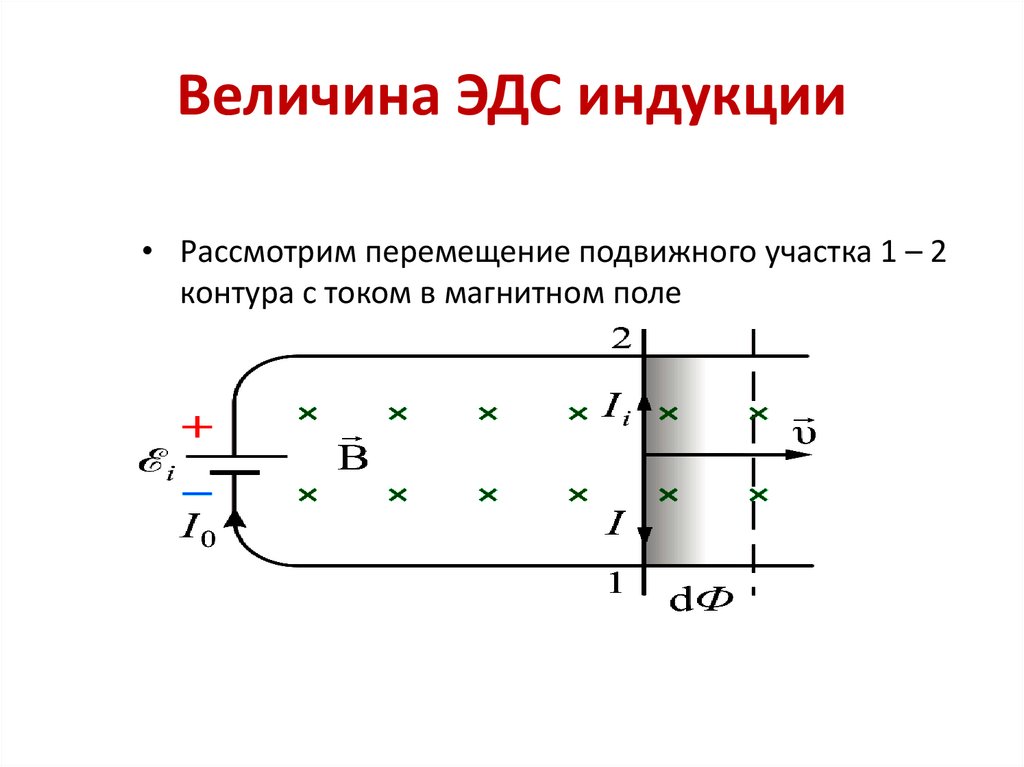
85. Величина ЭДС индукции
• Рассмотрим перемещение подвижного участка 1 – 2контура с током в магнитном поле
86. Величина ЭДС индукции
• Пусть сначала магнитное поле отсутствует.• Батарея с ЭДС равной E0 создает ток I0 .
• За время dt, батарея совершает работу:
dA E0 I 0dt
• – эта работа будет переходить в тепло которое
можно найти по закону Джоуля:
Q dA E0 I 0dt I 02 Rdt,
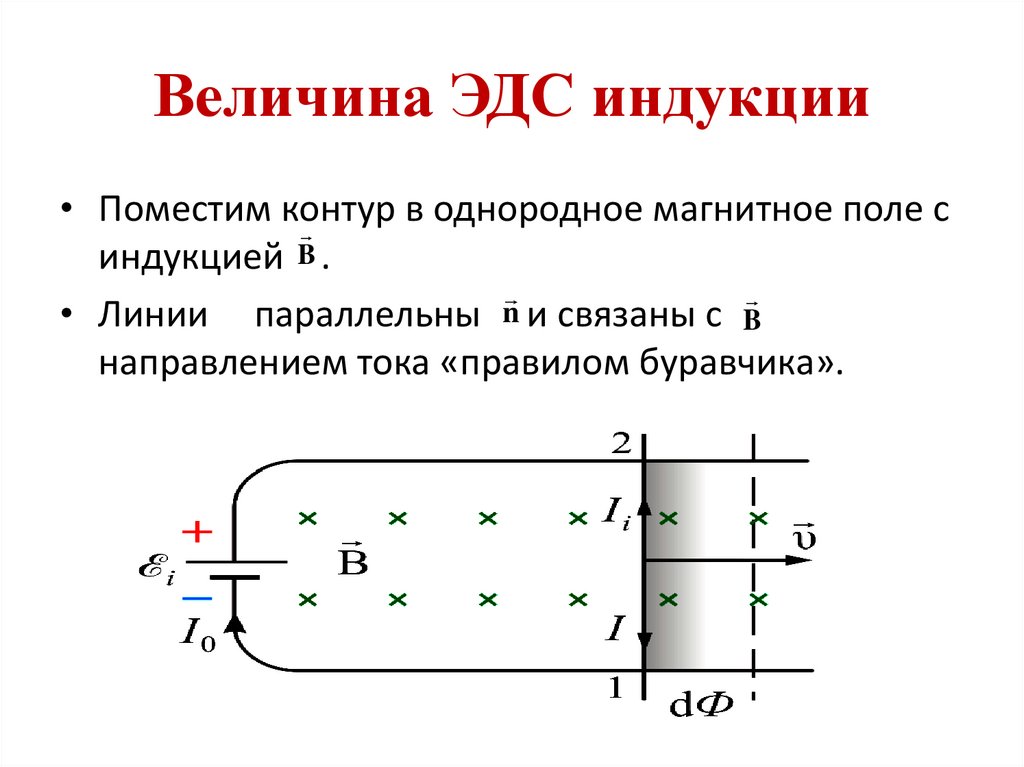
87. Величина ЭДС индукции
• Поместим контурв
однородное
магнитное
поле
с
индукцией B .
n
• Линии параллельны и связаны с B
направлением тока «правилом буравчика».
88. Величина ЭДС индукции
• Каждый элемент контура испытывает механическую силуdF
F0
• Подвижная сторона рамки будет испытывать силу
.
• Под действием этой силы участок 1 – 2 будет
перемещаться со скоростью dx / dt .
• При этом изменится и поток магнитной индукции.
• Тогда в результате электромагнитной индукции, ток в
контуре изменится и станет равным
I I0 Ii .
89. Величина ЭДС индукции
F0,• Изменится и сила
которая теперь станет равна
F– результирующая сила. Эта сила за время dt
произведет работу dA:
• Как и в случае, когда все элементы рамки
неподвижны, источником работы является ЭДС
батареи! .
dA Fdx ILBdx IdФ.
90. Величина ЭДС индукции
• При неподвижном контуре эта работа сводилась тольколишь к выделению тепла.
• При изменении магнитного потока тепло тоже будет
выделяться, но уже в другом количестве, так как ток
изменился.
• Кроме того, совершается механическая работа.
• Общая работа за время dt, равна:
E0 Idt I Rdt IdФ.
2
91. Величина ЭДС индукции
• Отсюда:I
dФ
dt
R
E0
• Полученное выражение это фактически закон Ома для
контура, в котором кроме источника действует ЭДС
индукции , которая равна:
Ei
dФ
.
dt
• ЭДС индукции контура равна скорости изменения потока
магнитной индукции, пронизывающей этот контур.
92. Выводы
• Сила Ампера совершает работу за счет ЭДСисточника тока.
• При этом в проводнике появляется ЭДС
индукции, которая уменьшает ток.
• Можно говорить, что ЭДС индукции
является следствием закона сохранения
энергии
93. Циркуляция вектора напряженности вихревого электрического поля
• Работу вихревого электрического поля по перемещениюзаряда вдоль замкнутого контура L можно подсчитать по
формуле
dA q E' d l .
L
• Работа по перемещению единичного заряда вдоль
замкнутой цепи равна ЭДС, действующей в этой цепи:
• Следовательно:
dA Ei
dФ
E' d l dt .
L
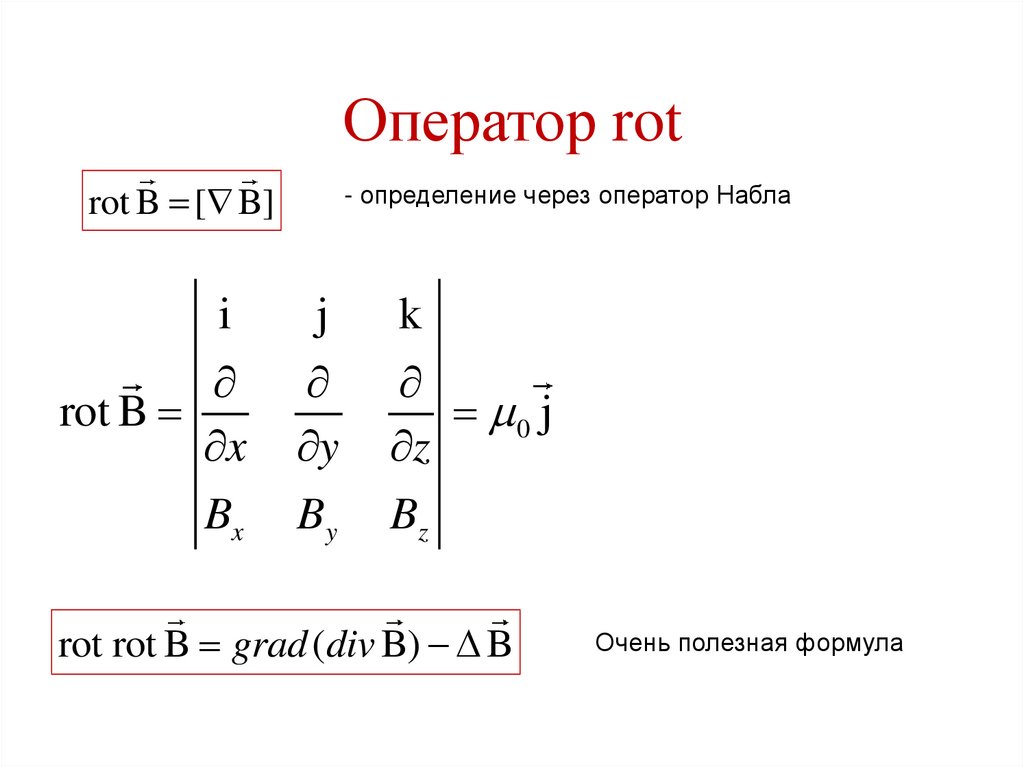
94. Оператор rot
rot B [ B]i
rot B
x
Bx
- определение через оператор Набла
j
y
By
k
0 j
z
Bz
rot rot B grad (div B) B
Очень полезная формула
95. Оператор rot
(rotF )n limS 0
Fdr
L
S
n – единичный вектор нормальный контуру L
S – площадь контура
(NB!) Направление обхода контура
выбирается так чтобы, если смотреть в
направлении n , контур L обходился по
часовой стрелке
96.
Основные уравнения магнитостатики• Основные уравнения магнитостатики для магнитных
полей, созданных постоянными потоками зарядов:
divB 0
Bds
0
S
Bdl
I
0
i
l
i
0 4 10 7 Гн/м
rotB μ 0 j






















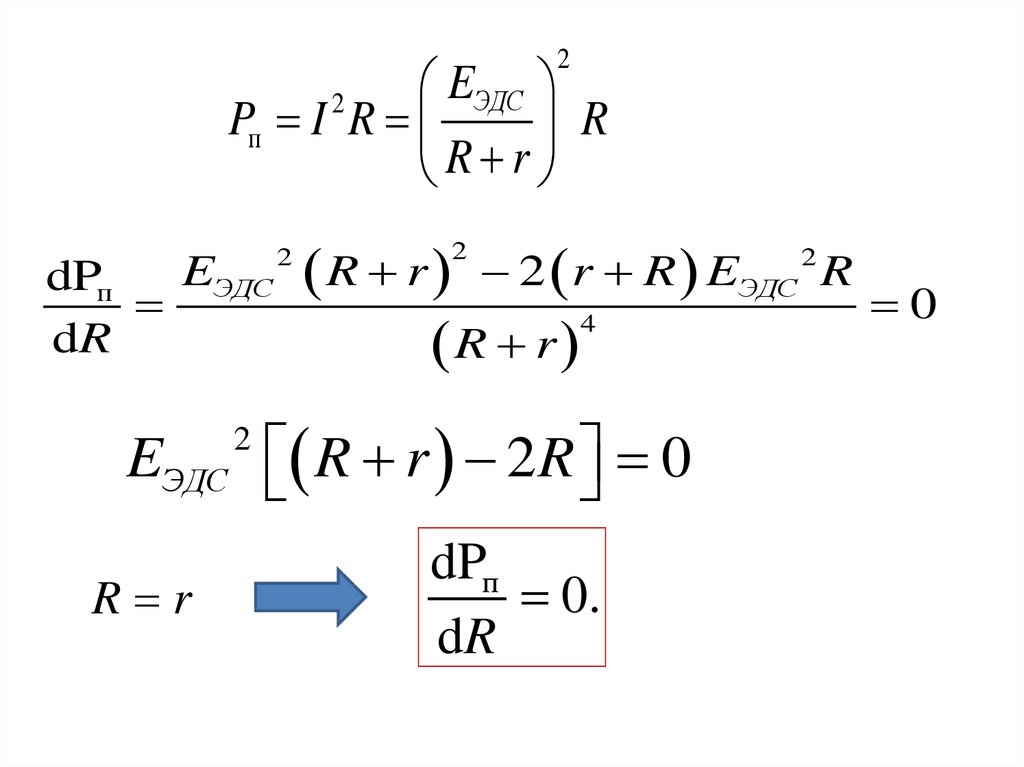













































 physics
physics








