Акустический метод

1. Дисциплина «Промысловая геофизика». Акустический метод Лектор: доц. Лобова Г.А.

1 1
Слайд

2. Физические основы АМ

Акустический каротаж (АК) – это совокупность
методов, основанных на изучении кинематических и
динамических характеристик упругих волн (деформаций) ,
возбуждаемых в скважине импульсным источником.
Горная порода рассматривается , в основном, как
упругое тело. Упругое тело характеризуется тем, что при
снятии приложенных сил, деформации восстанавливаются.
В однородной изотропной среде
распространяются волны двух типов:
- продольная волна – P-волна
- поперечная волна – S-волна
возникают
и
Слайд 2

3. Физические основы АМ

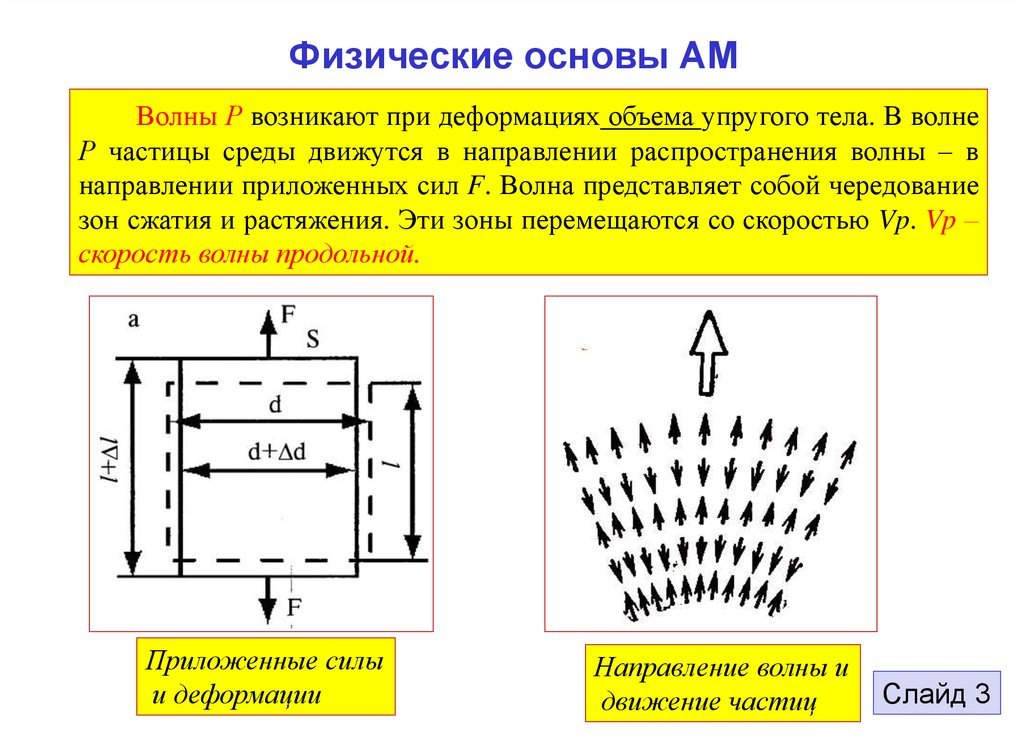
Волны Р возникают при деформациях объема упругого тела. В волне
Р частицы среды движутся в направлении распространения волны – в
направлении приложенных сил F. Волна представляет собой чередование
зон сжатия и растяжения. Эти зоны перемещаются со скоростью Vp. Vp –
скорость волны продольной.
Приложенные силы
и деформации
Направление волны и
3
движение частиц
Слайд 3

4. Физические основы АМ

Упругие константы – физико-механические характеристики
горных пород:
Е – модуль упругости Юнга (модуль линейного растяжения).
Характеризует сопротивление горной породы изменению объема.
μ – коэффициент Пуассона (модуль поперечного сжатия, отношение
поперечного сжатия к продольному растяжению). Характеризует
сопротивление горной породы изменению формы.
E= (F/S)/ (▲l/l )
μ = (▲ d/d)/ (▲l/l )
Слайд 4

5. Физические основы АМ

Волны S возникают при деформациях формы (сдвига) упругого тела.
В волне S частицы среды движутся в направлении перпендикулярном
распространению волны – в направлении приложенных сил F.
Наблюдается чередование полос с противоположным направлением
движения частиц. Эти зоны (полосы) перемещаются со скоростью Vs. Vs
– скорость волны поперечной.
Приложенные силы
и деформации
Направление волны и
5
движение частиц
Слайд 5

6. Физические основы АМ

Упругие константы – физико-механические характеристики
горных пород:
G – модуль сдвига (отношение сдвигового напряжения к сдвиговой
деформации).
k – объемный модуль всестороннего сжатия.
G= (F/S) / tg(γ)
k= (1/3)E/ (1- 2μ )
G = (3/2)k(1-2 μ )/ (1+ μ)
Слайд 6

7. Физические основы АМ

Модуль сдвига G, модуль Юнга E и коэффициент Пуассона σ
связаны между собой.
μ – коэффициент Пуассона можно определить на основе
измерения скоростей Vp и Vs.
G= E/2(1+ μ)
μ = 0,5(V2p-2V2s)/ (V2p-V2s)
Слайд 7

8.

Физические основы АМ
а - продольная волна Р- поступательного движения частиц среды в направлении распространения
упругих колебаний (волны).
б - поперечная волна S - движения частиц среды в направлении перпендикулярном
распространению упругих колебаний (волны).
Слайд 8

9.

Физические основы АМ
Продольные волны распространяются со скоростью Vp,
определяемой упругими и плотностными свойствами среды:
E (1 )
2
Vp
(1 )(1 2 )
E – модуль Юнга;
μ – коэффициент Пуассона;
λ – константа Ламе;
σ – плотность среды.
Константы λ и μ, обусловливающие жесткость среды, при
уплотнении пород растут быстрее плотности σ. Поэтому
увеличение плотности сопровождается обычно возрастанием
акустической скорости.
Слайд 9

10.

Физические основы АМ
Поперечные волны распространяются со скоростью VS,
определяемой упругими и плотностными свойствами среды:
1
Vs
2(1 )
E
2
Vp
Vs
Константы λ и μ, всегда положительны, поэтому скорости
продольных волн всегда больше скоростей поперечных.
Для горных пород в среднем VP / VS = 1,7.
Слайд 10

11.

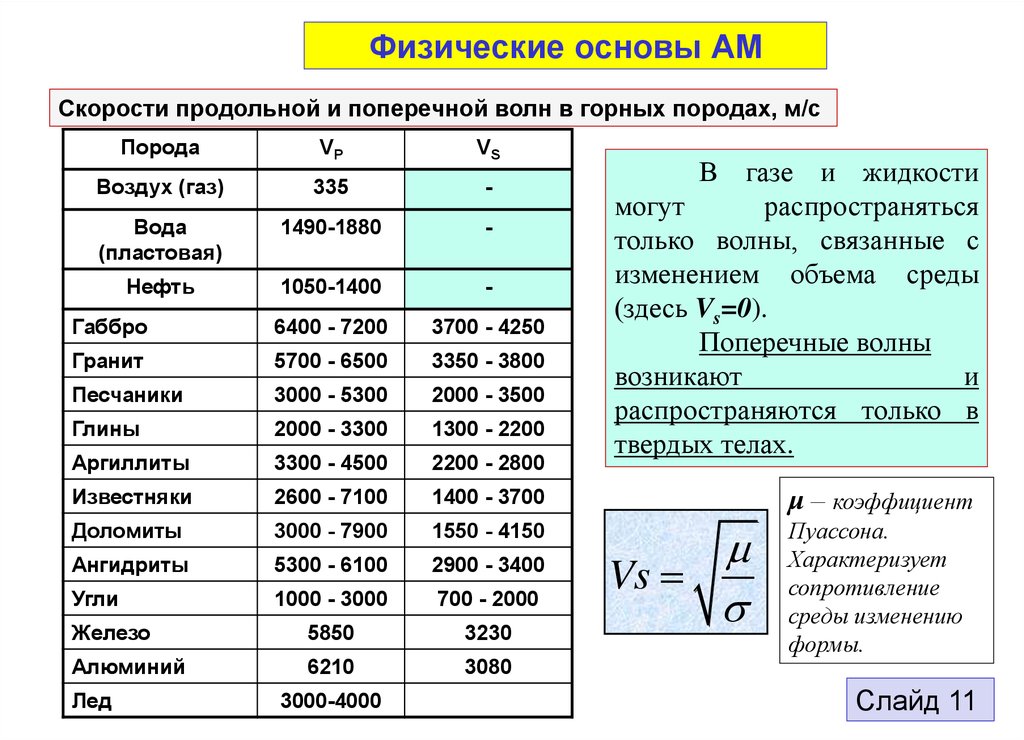
Физические основы АМ
Скорости продольной и поперечной волн в горных породах, м/с
Порода
VP
VS
Воздух (газ)
335
-
Вода
(пластовая)
1490-1880
-
Нефть
1050-1400
-
Габбро
6400 - 7200
3700 - 4250
Гранит
5700 - 6500
3350 - 3800
Песчаники
3000 - 5300
2000 - 3500
Глины
2000 - 3300
1300 - 2200
Аргиллиты
3300 - 4500
2200 - 2800
Известняки
2600 - 7100
1400 - 3700
Доломиты
3000 - 7900
1550 - 4150
Ангидриты
5300 - 6100
2900 - 3400
Угли
1000 - 3000
700 - 2000
Железо
5850
3230
Алюминий
6210
3080
Лед
3000-4000
В газе и жидкости
могут
распространяться
только волны, связанные с
изменением объема среды
(здесь Vs=0).
Поперечные волны
возникают
и
распространяются только в
твердых телах.
μ – коэффициент
Vs
Пуассона.
Характеризует
сопротивление
среды изменению
формы.
Слайд 11

12.

Физические основы АМ
Скорость распространения упругих волн V в пористых
горных
породах
с
поровым
пространством,
заполненным флюидом (формула Уайли, формула среднего
времени):
1 kп 1 kп
,
V Vж
Vм
где: kп – коэффициент пористости породы; Vж –скорость
распространения упругих волн в жидкости (флюиде),
заполняющей поровое пространство; Vм – скорость
распространения упругих волн в минеральном скелете.
Слайд 12

13.

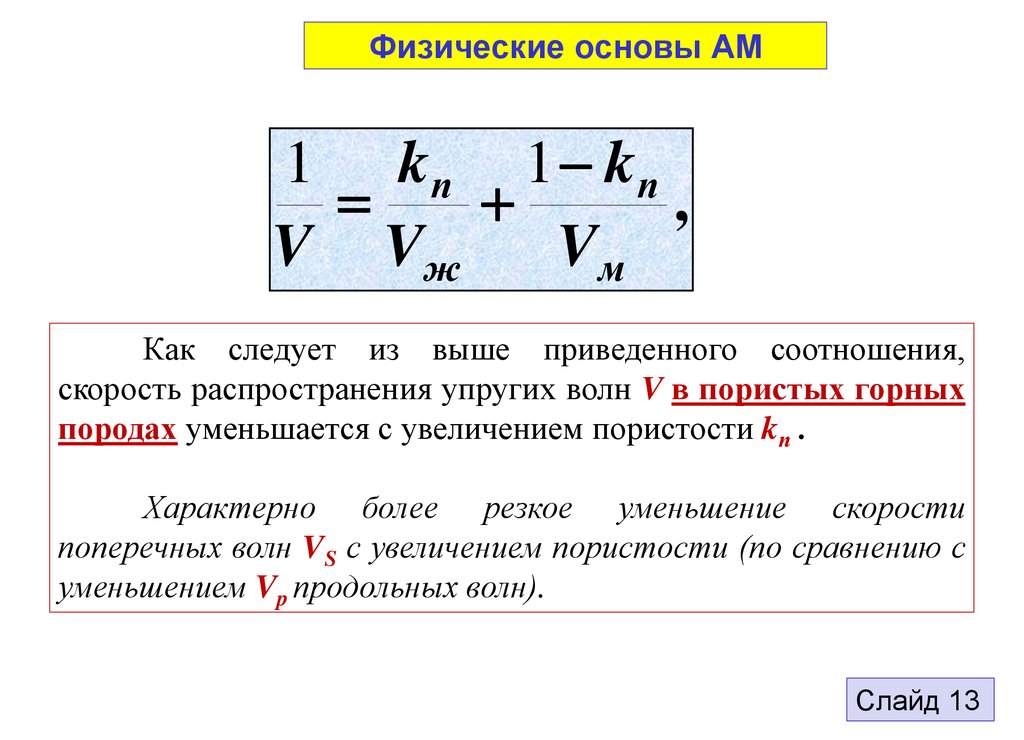
Физические основы АМ
1 kп 1 kп
,
V Vж
Vм
Как следует из выше приведенного соотношения,
скорость распространения упругих волн V в пористых горных
породах уменьшается с увеличением пористости kп .
Характерно более резкое уменьшение скорости
поперечных волн VS с увеличением пористости (по сравнению с
уменьшением Vp продольных волн).
Слайд 13

14.

Физические основы АМ
Величина скорости V в пористых горных породах зависит от
характера флюида, заполняющего поровое пространство
(индексы в, н, г –означают водо- нефте- и газонасыщение):
VP ( в ) VP ( н ) VP ( г ) ,
VS ( в ) VS ( н ) VS ( г ) .
Дифференциация различно насыщенных коллекторов (водо- нефте- и
газонасыщение) по скоростям колеблется от 0 до 20 %.
Слайд 14

15.

Физические основы АМ
Дисперсия скорости – это зависимость
скорости от частоты волны.
Общая тенденция для основных типов пород
(близкая к линейной) – с ростом частоты колебаний
растет скорость акустической волны.
Степень дисперсии зависит от характера флюида,
заполняющего поровое пространство.
Дисперсия при частотах 15 и 35 КГц:
- при заполнении пор газом разница скоростей может
достигать 40%;
- при заполнении пор нефтью разница скоростей
может достигать – 10%;
- при заполнении пор пластовой водой – дисперсия
проявляется слабо.
Слайд 15

16.

РАСПРОСТРАНЕНИЕ ПРОДОЛЬНОЙ ВОЛНЫ ОТ ТОЧЕЧНОГО ИСТОЧНИКА
задний фронт (тыл)
N
передний фронт (фронт)
M
О
Магнитострикционный
импульсный
излучатель
(источник).
Используется
эффект изменения объема и
формы тела при пропускании
переменного тока.
Длительность импульса 1 – 3 периода
(Т) с частотой f=5 КГц– 2 МГц.
Слайд 16

17.

РАСПРОСТРАНЕНИЕ ПРОДОЛЬНОЙ ВОЛНЫ ОТ ТОЧЕЧНОГО ИСТОЧНИКА
задний фронт (тыл)
передний фронт (фронт)
О
Фронт (Ф) – та часть среды,
куда деформации еще не
дошли.
Тыл (Т) – та часть
среды, где деформации
уже прекратились
Колеблющиеся частицы внутри сферического слоя
образуют концентрические зоны сжатия и
растяжения, чередующиеся друг с другом. В
данном примере (а и б) таких зон четыре, причем
у фронта волны (Ф) распространяется зона
сжатия, а у тыла волны (Т) - зона растяжения.
Слайд 17

18.

РАСПРОСТРАНЕНИЕ ПРОДОЛЬНОЙ ВОЛНЫ ОТ ТОЧЕЧНОГО ИСТОЧНИКА.
ИЗОБРАЖЕНИЕ ВОЛНЫ – ПРОФИЛЬ ВОЛНЫ.
сжатие
растяжение
сжатие
растяжение
Профиль волны – up(r) показывает
для фиксированного момента
времени (t=const) внутри области
(δr)
зависимость амплитуды величины смещения частиц среды
(U) от их расстояния до источника
(r).
Расстояние
между
соседними
фазами
одноименными
экстремумами
профиля
(максимумами
или
минимумами)
видимая
(преобладающая) длина волны λв.
r
- расстояние до тыла волны.
расстояние до фронта волны.
T
r
ф
-
Слайд 18

19.

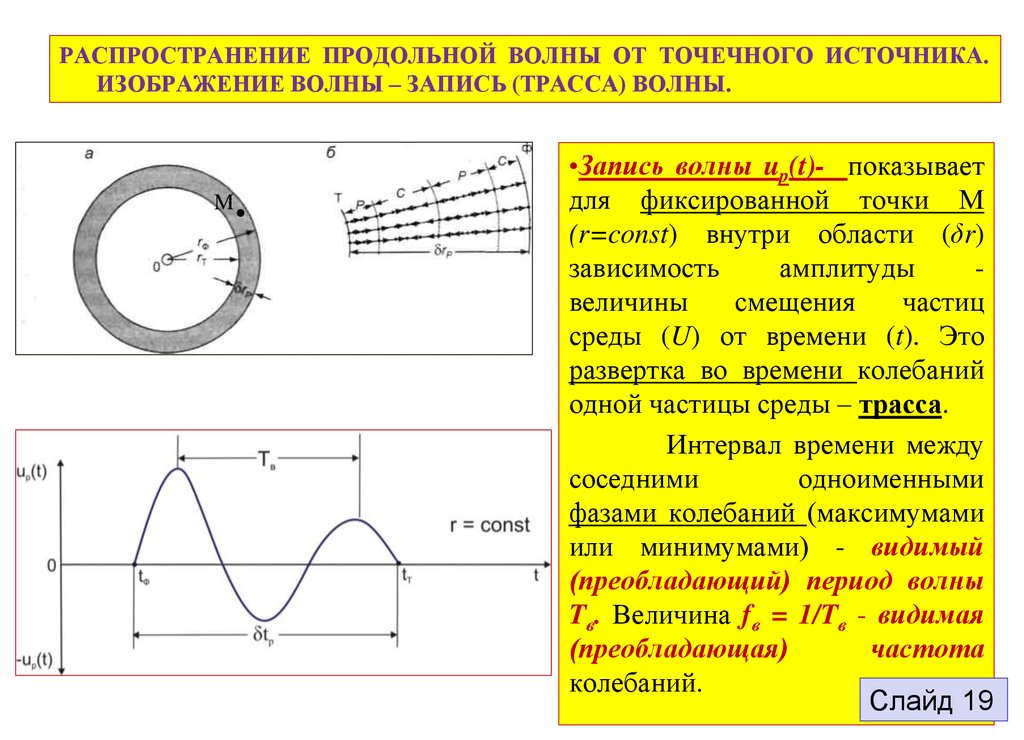
РАСПРОСТРАНЕНИЕ ПРОДОЛЬНОЙ ВОЛНЫ ОТ ТОЧЕЧНОГО ИСТОЧНИКА.
ИЗОБРАЖЕНИЕ ВОЛНЫ – ЗАПИСЬ (ТРАССА) ВОЛНЫ.
M
•Запись волны up(t)- показывает
для фиксированной точки М
(r=const) внутри области (δr)
зависимость
амплитуды
величины
смещения
частиц
среды (U) от времени (t). Это
развертка во времени колебаний
одной частицы среды – трасса.
Интервал времени между
соседними
одноименными
фазами колебаний (максимумами
или минимумами) - видимый
(преобладающий) период волны
Tв. Величина fв = 1/Tв - видимая
(преобладающая)
частота
колебаний.
Слайд 19

20.

РАСПРОСТРАНЕНИЕ ПРОДОЛЬНОЙ ВОЛНЫ ОТ ТОЧЕЧНОГО ИСТОЧНИКА.
ЗАПИСЬ (ТРАССА) ВОЛНЫ.
M
Как и для профиля волны, так и для трассы, характерные точки ее
записи (экстремумы, нули) называют фазами волны. Момент tФ начала
колебаний в точке наблюдения М является временем первого вступления
волны (фронт), а момент tТ - временем прекращения колебаний (тыл).
Интервал времени δtp = tТ - tФ есть длительность колебаний.
Слайд 20

21.

РАСПРОСТРАНЕНИЕ ПРОДОЛЬНОЙ ВОЛНЫ ОТ ТОЧЕЧНОГО ИСТОЧНИКА.
ИЗОБРАЖЕНИЕ ВОЛНЫ – ЗАПИСЬ (ТРАССА) ВОЛНЫ.
ФАЗОВАЯ КОРРЕЛЯЦИЯ ВОЛН
Прослеживание одинаковых колебаний (фаз) одной и
той же волны в различных точках среды (на небольшом
расстоянии), путем сопоставления формы колебаний,
называется фазовой корреляцией.
Линия, соединяющая одинаковые фазы одной и той же
волны на соседних трассах, называется осью синфазности.
Слайд 21

22. ФАЗОВАЯ КОРРЕЛЯЦИЯ ВОЛН

РАСПРОСТРАНЕНИЕ ПРОДОЛЬНОЙ ВОЛНЫ ОТ ТОЧЕЧНОГО ИСТОЧНИКА.
ЗАПИСЬ (ТРАССА) ВОЛНЫ.
ФАЗОВАЯ КОРРЕЛЯЦИЯ ВОЛН
M2
M1
U(t)
M1
U(t)
M2
Изображены трассы, показывающие
смещение частиц среды U(t) за время t в
фиксированных точках М1(r=r1) и М2(r=r2). В
точке М2 амплитуда волны меньше, т.к. точка
М2 дальше расположена от источника.
Штрих-пунктиром
проведены
(прослежены) оси фазовой корреляции – оси
синфазности.
Первое отклонение в момент времени
t1 называется первым вступлением волны.
Слайд 22

23. СПОСОБЫ ИЗОБРАЖЕНИЯ акустических колебаний (записей, трасс): а) способ отклонений; б) способ переменной ширины; в) способ

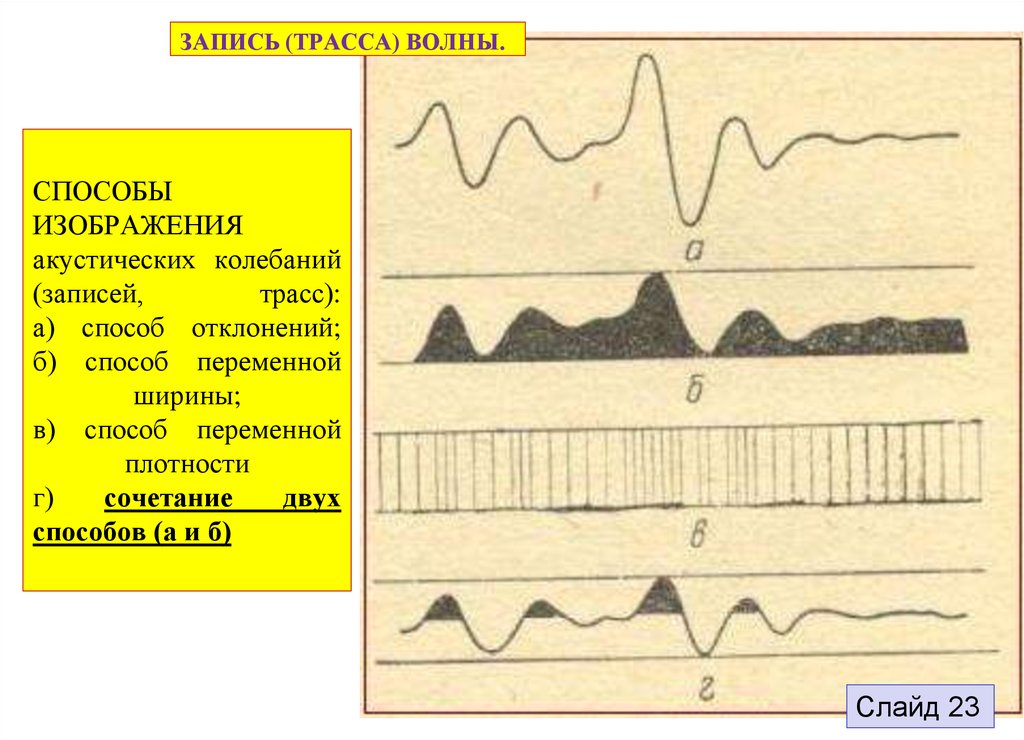
ЗАПИСЬ (ТРАССА) ВОЛНЫ.
СПОСОБЫ
ИЗОБРАЖЕНИЯ
акустических колебаний
(записей,
трасс):
а) способ отклонений;
б) способ переменной
ширины;
в) способ переменной
плотности
г)
сочетание
двух
способов (а и б)
Слайд 23

24. Вид осей синфазности при записи способом отклонения и переменной ширины

ЗАПИСЬ (ТРАССА) ВОЛНЫ.
Вид
осей синфазности
при записи
способом
отклонения и
переменной ширины
Слайд 24

25. Изохроны (поверхности, линии равного времени прихода) сферической волны при точечном источнике в трехмерном пространстве (а) и

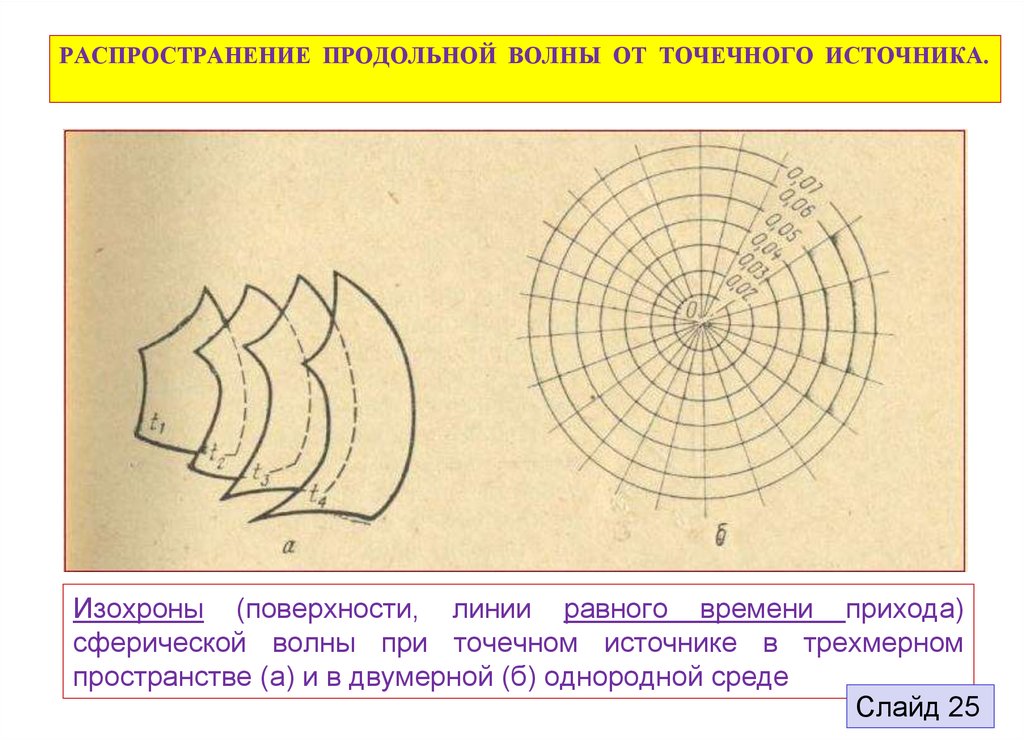
РАСПРОСТРАНЕНИЕ ПРОДОЛЬНОЙ ВОЛНЫ ОТ ТОЧЕЧНОГО ИСТОЧНИКА.
Изохроны (поверхности, линии равного времени прихода)
сферической волны при точечном источнике в трехмерном
пространстве (а) и в двумерной (б) однородной среде
Слайд 25

26.

ЗАТУХАНИЕ УПРУГИХ ВОЛН
За счет поглощения , геометрического расхождения и потерь энергии на
отражение и преломление происходит затухание сферических упругих
волн:
A1 A0 e
x
,
(1)
А0 – начальное значение амплитуды (x
0);
x – расстояние от излучателя до точки наблюдения (регистрации);
α – коэффициент затухания.
Слайд 26

27. ПОНЯТИЕ ПЛОСКОЙ ВОЛНЫ

r
A1 A0 e
x
,
На больших удалениях от
сферического источника (r →∞)
кривизна
фронта
волны
становится незначительной, и его
поверхность
практически
вырождается в плоскость.
В такой плоской волне
амплитуда
колебаний
А
практически не изменяется с
расстоянием (α→0), поскольку
геометрическое
расхождение
несущественно.
Слайд 28

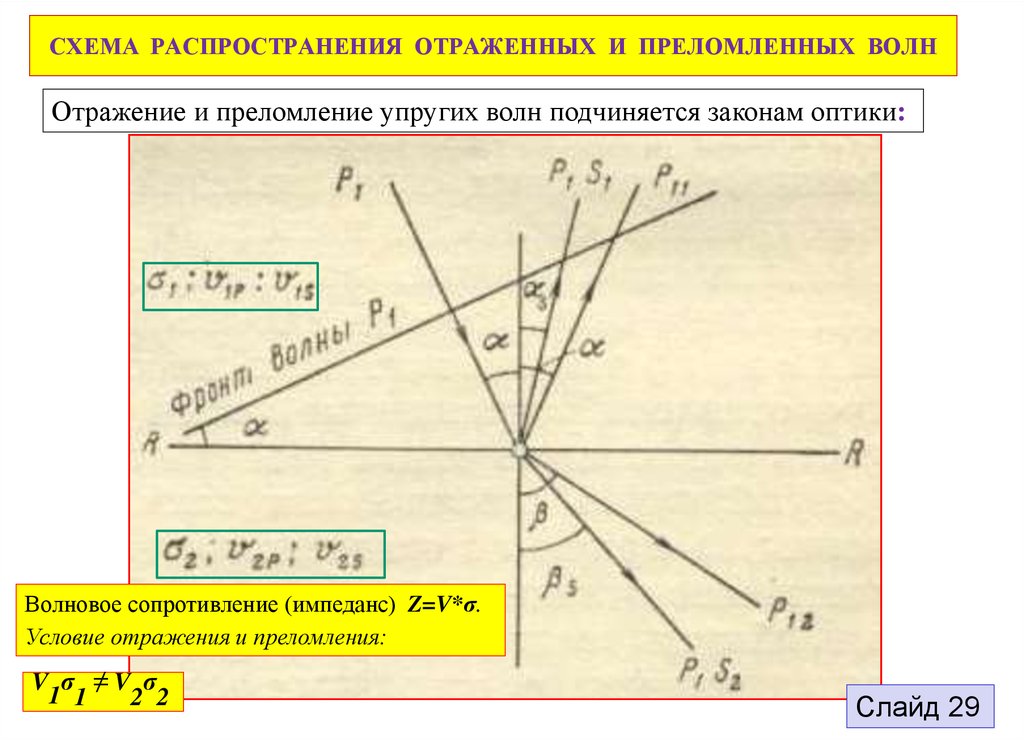
28. СХЕМА РАСПРОСТРАНЕНИЯ ОТРАЖЕННЫХ И ПРЕЛОМЛЕННЫХ ВОЛН

Отражение и преломление упругих волн подчиняется законам оптики:
Волновое сопротивление (импеданс) Z=V*σ.
Условие отражения и преломления:
V σ ≠V σ
1 1
2 2
Слайд 29

29.

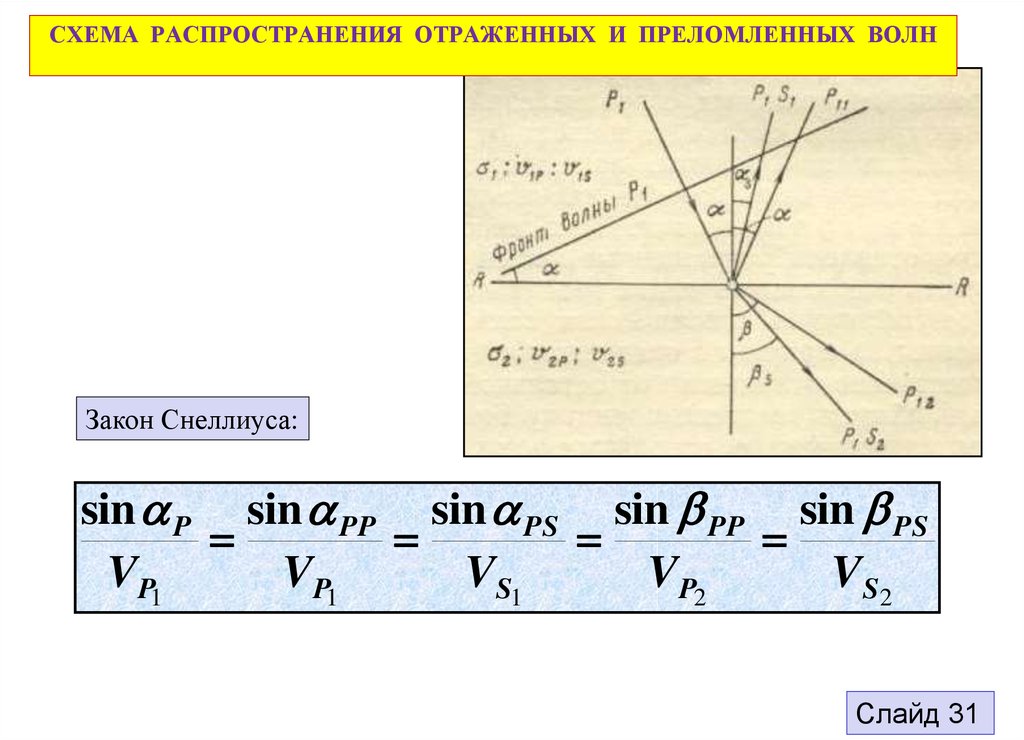
СХЕМА РАСПРОСТРАНЕНИЯ ОТРАЖЕННЫХ И ПРЕЛОМЛЕННЫХ ВОЛН
Любая волна, падающая на
границу раздела σ1, V1p, V1s /
σ2, V2p, V2s, порождает 4-е
волны: 2-е отраженные и 2-е
преломленные:
P1 – падающая продольная волна
P11 , P1 S1 – отраженные волны
P12 , P2 S2 – преломленные волны
P11 , P12 – монотипные волны
P1 S1 , P2 S2 – обменные волны
α – угол падения
α,αs – угол отражения
β, β s - угол преломления
Слайд 30

30.

СХЕМА РАСПРОСТРАНЕНИЯ ОТРАЖЕННЫХ И ПРЕЛОМЛЕННЫХ ВОЛН
Закон Снеллиуса:
sin P sin PP sin PS sin PP sin PS
VP1
VP1
VS1
VP2
VS2
Слайд 31

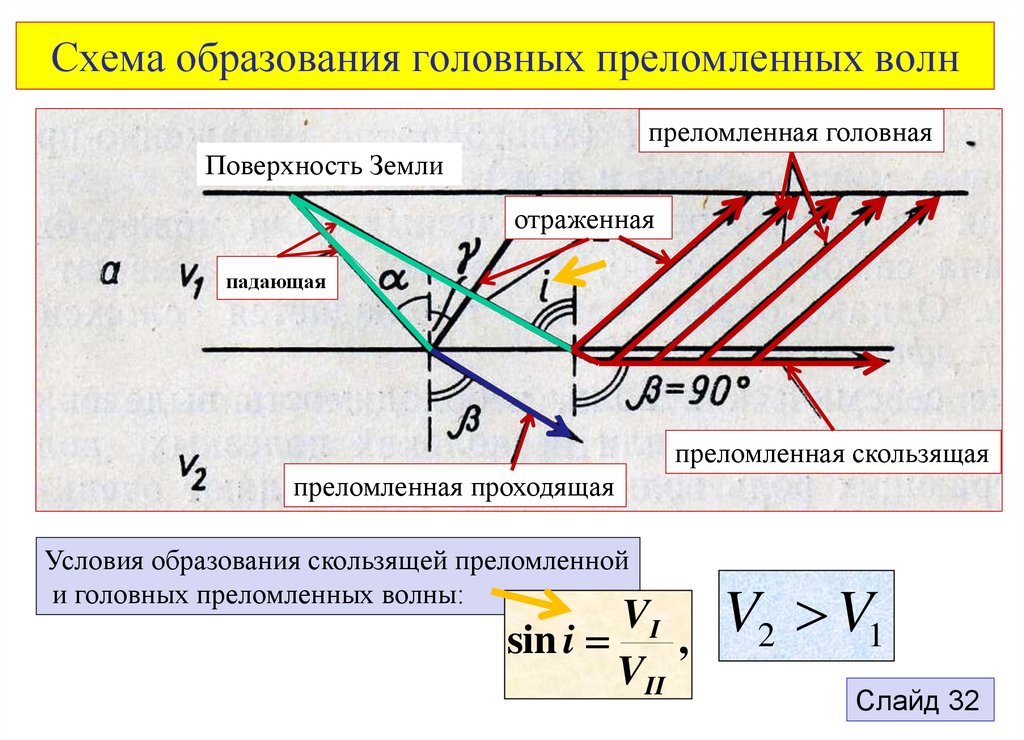
31. Схема образования головных преломленных волн

преломленная головная
Поверхность Земли
отраженная
падающая
преломленная скользящая
преломленная проходящая
Условия образования скользящей преломленной
и головных преломленных волны:
VI
sin i
,
VII
V2 V1
Слайд 32

32. Схема образования головных преломленных волн

Каждая точка фронта скользящей
преломленной волны порождает головную
преломленную волну (принцип Гюйгенса).
i – критический угол (угол полного
внутреннего отражения).
Образование скользящей поперечной
волны аналогично.
VI
sin i
,
VII
V2 V1
Слайд 33