Конические сечения

1. Конические сечения

Ученицы 11 класса
Ивановой Екатерины
Учитель Сидько Светлана
Николаевна

2.

Коническое сечение или коника есть пересечение плоскости с
круговым конусом. Существует три главных типа конических
сечений: эллипс, парабола и гипербола, кроме того существуют вырожденные
сечения: точка, прямая и пара прямых.
Открывателем конических сечений предположительно считается Менехм,ученик
Платона и учитель Александра Македонского.
Аполлоний Пергский – ученый , который изучал конические сечения.

3.

Менехм обнаружил новые кривые, занимаясь проблемой удвоения
куба. Связь с этой проблемой легко понять: для удвоения куба
требуется извлечение кубического корня, а оно недостижимо с
помощью циркуля и линейки; однако если в класс допустимых
кривых (прямые и окружности) добавить конические сечения, то
построение кубических корней выполнить несложно.
Алгебраически это означает, например, что для решения
уравнения
x3 =a мы находим точку пересечения
кривых
y=x2
(парабола) и y=
a/x (гипербола).

4.

Титульный лист одной из реконструкций VIII
книги «Конических сечений»

5.

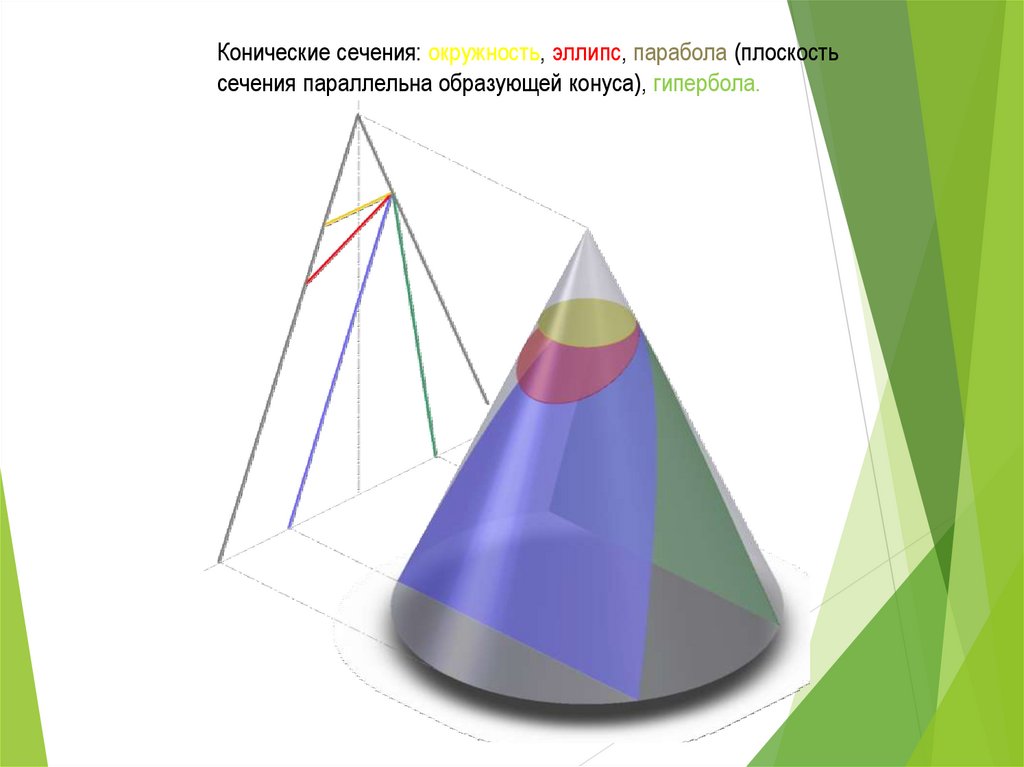
Конические сечения: окружность, эллипс, парабола (плоскость
сечения параллельна образующей конуса), гипербола.

6.

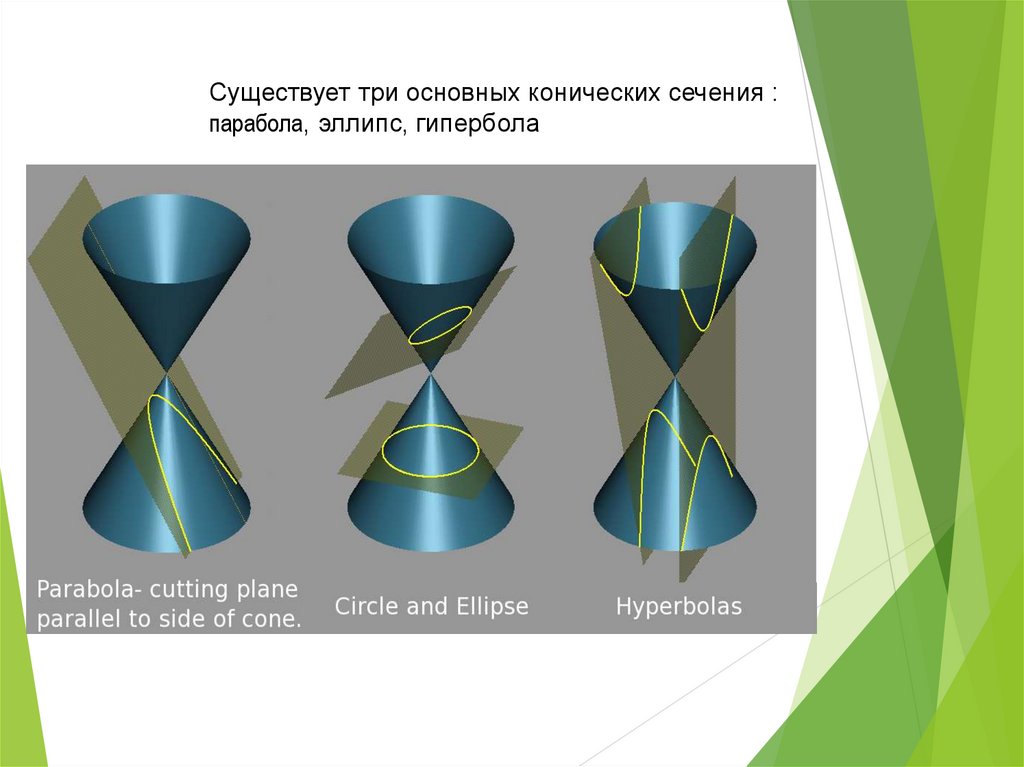
Существует три основных конических сечения :
парабола, эллипс, гипербола

7.

Для данного конуса рассмотрим коническую поверхность,
образованную прямыми, проходящими через вершину конуса и
точки окружности основания конуса.
Сечения конической поверхности плоскостью можно
рассматривать как центральную проекцию окружности
основания конуса на эту плоскость. Поэтому, если плоскость
параллельна плоскости основания и не проходит через
вершину конуса, то в сечении конической поверхности
получается окружность.

8.

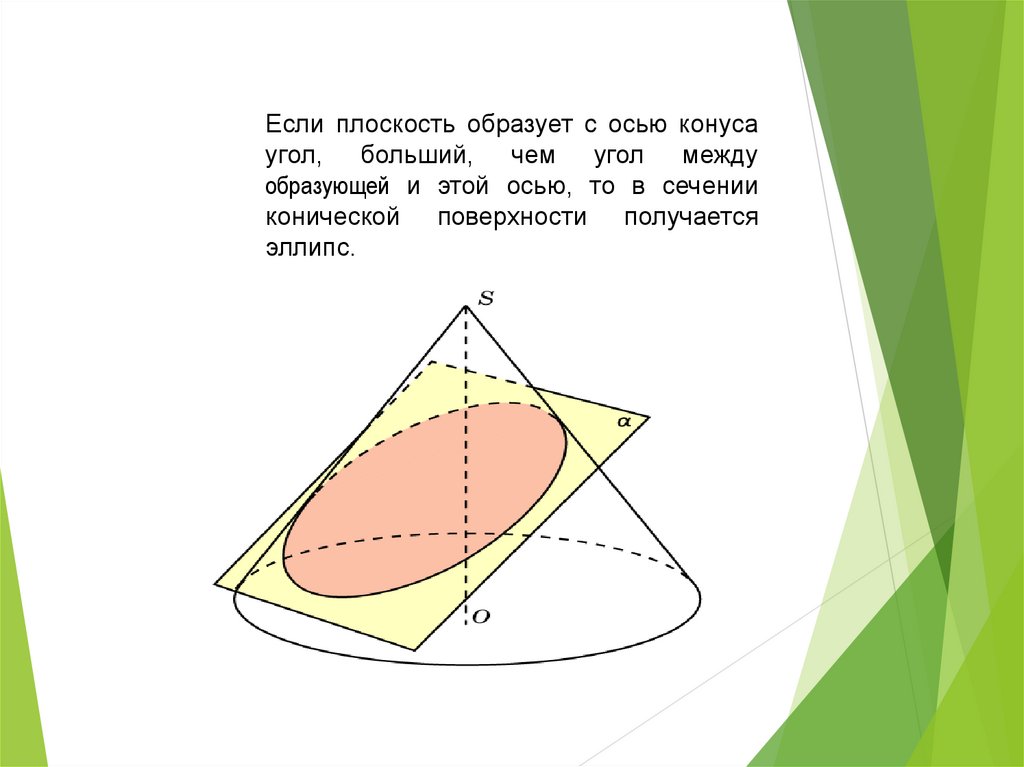
Если плоскость образует с осью конуса
угол, больший, чем угол между
образующей и этой осью, то в сечении
конической поверхности получается
эллипс.

9.

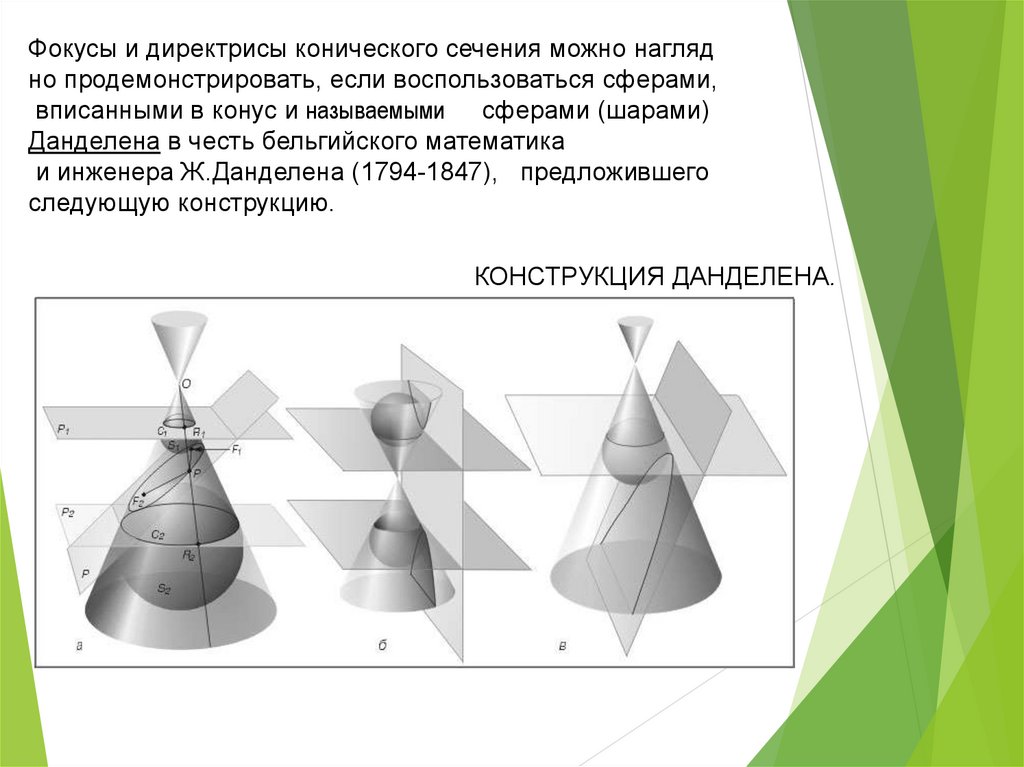
Фокусы и директрисы конического сечения можно нагляд
но продемонстрировать, если воспользоваться сферами,
вписанными в конус и называемыми сферами (шарами)
Данделена в честь бельгийского математика
и инженера Ж.Данделена (1794-1847), предложившего
следующую конструкцию.
КОНСТРУКЦИЯ ДАНДЕЛЕНА.

10.

ВЫРОЖДЕННЫЕ КОНИЧЕСКИЕ СЕЧЕНИЯ. Две пере
секающиеся прямые образуют вырожденную
гиперболу (а). Два вырожденных эллипса (б) возникают,
когда конус пересекается с плоскостью,
параллельной его основанию.

11.

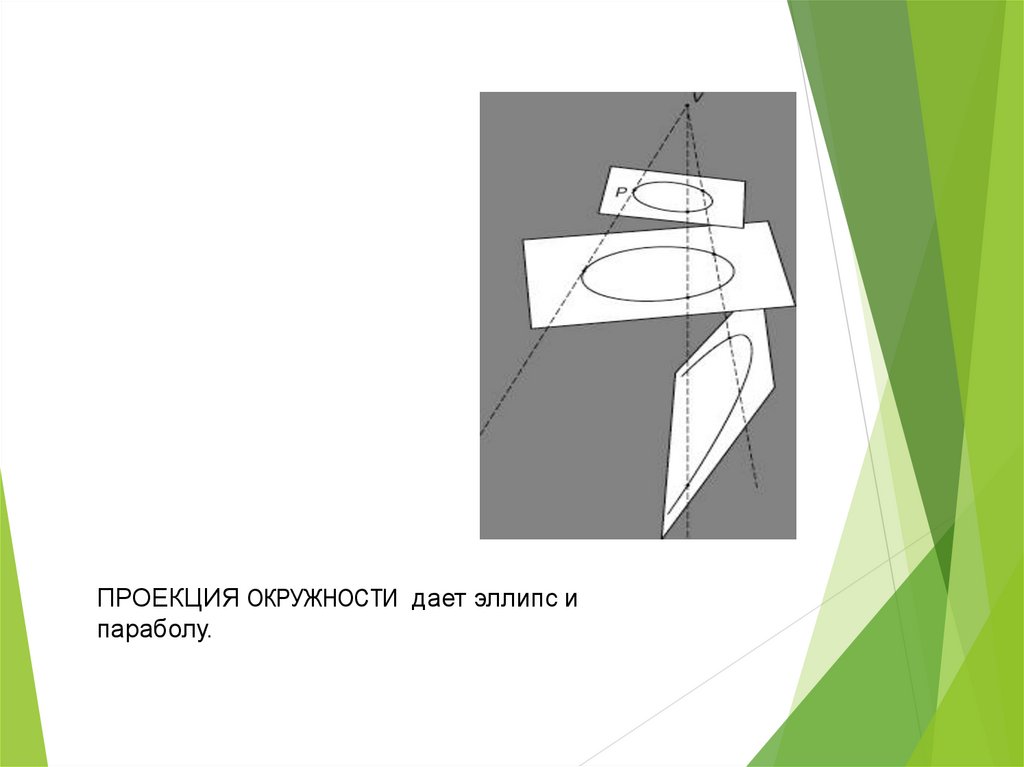
ПРОЕКЦИЯ ОКРУЖНОСТИ дает эллипс и
параболу.

12. Спасибо за внимание!