Пирамидальная сортировка HeapSort. Пирамида Хеопса

1. Пирамидальная сортировка HeapSort

Пирамида Хеопса

2. Пирамидальная сортировка или метод Вильямса – Флойда ( Williams, Floyd, 1964)

Пирамидальная сортировка основана на
алгоритме построения пирамиды.
Определение
Последовательность aL , aL+1 , … , aR
называется пирамидой, если неравенство
ai ≤ min (a2i , a2i+1 )
выполняется для всех i, для которых хотя бы
один из элементов a2i и a2i+1 существует.

3. Пример

2
3
4
5
6
7
8
3 2 6 3 4 5 7
1
2
3
4
5
6
7
- пирамида
- не пирамида
Свойства пирамиды
1. Двустороннее усечение:
Если последовательность aL, aL+1 , ..., аR-1, aR –
пирамида, то aL+1 , ..., aR-1 тоже пирамида.
2. Если a1 , a2 , ..., an – пирамида,
то а1 – минимальный элемент пирамиды.
3. Если a1 , ..., an – произвольная
последовательность, то an/2 , .., an – пирамида.

4. Построение пирамиды

Пусть aL+1 , …, aR - пирамида,
необходимо добавить элемент Х,
чтобы получить новую пирамиду aL , …, aR.
Новый элемент добавляем в начало, расширяя
последовательность влево.
Если aL удовлетворяет условию пирамиды, то
пирамида построена.

5. Построение пирамиды

Иначе найдутся такие a2L или a2L+1 , что не будут
удовлетворять условию пирамиды.
Возьмем минимальный элемент из a2L и a2L+1 ,
обозначим его за aj и обменяем с aL .
В результате получим a’L ≤ a2L и a’L ≤ a2L+1 , что
удовлетворяет условию пирамиды.

6. Построение пирамиды

Теперь элемент Х попал на место aj и для него
необходимо проверить условие пирамиды, и
так до конца массива.
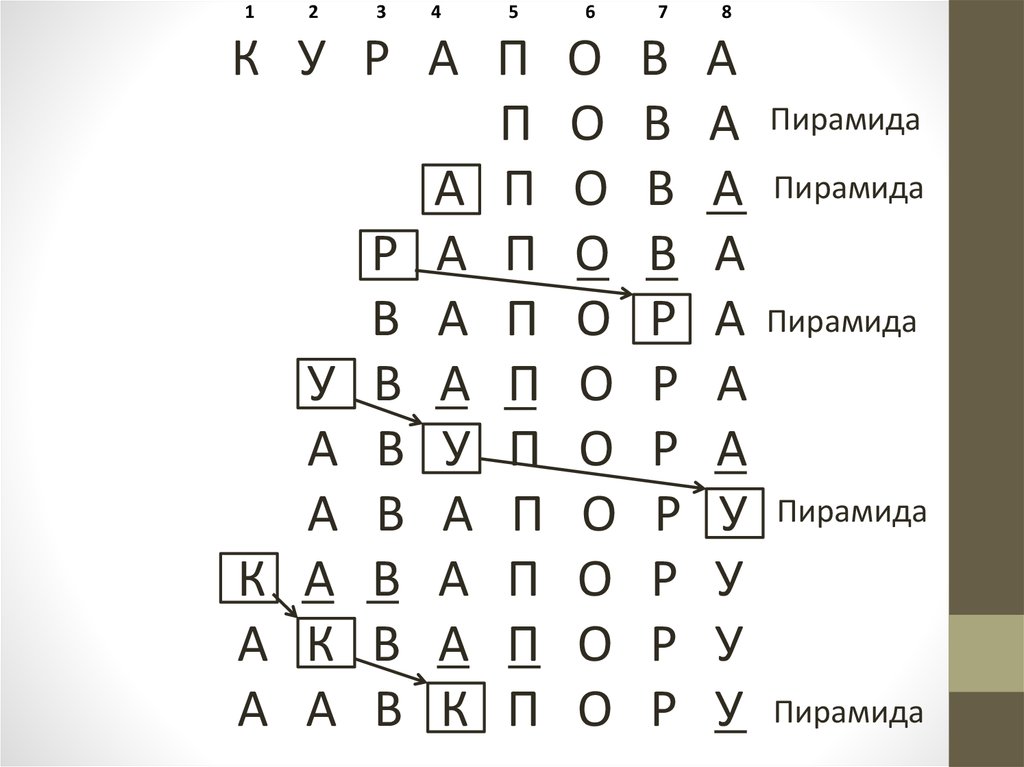
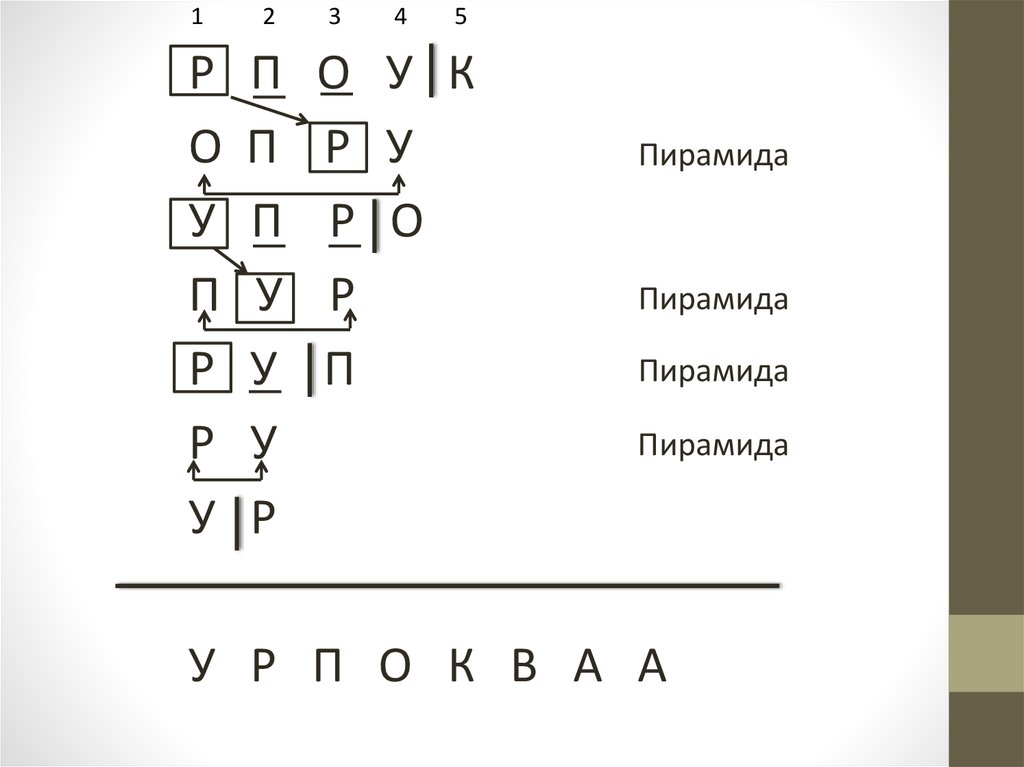
Пример:
1
2
3
4
5
6
7
8
3
6 3
2 3
2 3
2
2
6
4
6
6
6
6
3
3
3
3
4
4
4
6
5
5
5
5
7
7
7
7
Пирамида
Пирамида

7. Построение пирамиды (L ,R) Алгоритм на псевдокоде

aL+1, …, a R – на входе пирамида (L+1,R)
aL – новый элемент
x := aL, i := L
DO
j := 2i
IF ( j>R) OD FI
IF ( j<R и aj+1 aj ) j=j+1 FI
IF ( x aj ) OD FI
ai= aj
i:=j
OD
ai:=x

8.

Трудоемкость алгоритма
построения пирамиды
Определим верхнюю границу трудоемкости
алгоритма. На каждой итерации цикла
выполняется максимум два сравнения и одна
пересылка. Найдем наибольшее количество
итераций ( k ). Наихудший случай, когда в
перестановках участвуют элементы aL , a2L , a4L …
aL … a2L a2L+1 … a4L a4L+1 … am amL+1 … aR
21
mL ≤ R
22
2