Смежные и вертикальные углы

1. Смежные и вертикальные углы

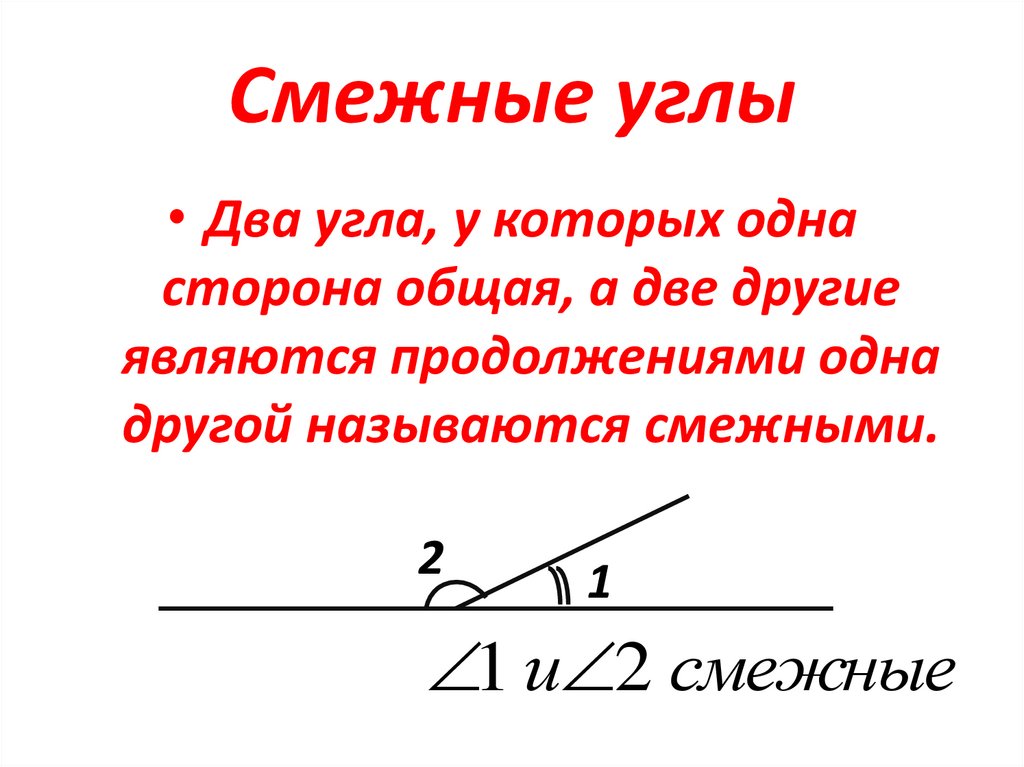
2. Смежные углы

• Два угла, у которых одна
сторона общая, а две другие
являются продолжениями одна
другой называются смежными.
2
1
1 и 2 смежные

3.

Теорема: Сумма смежных углов равна
180
В
Дано:<1 и<2смежные
Доказать:<1+<2=180
1 2
А
О
С Доказательство:
Обозначим углы <АОВ и <ВОС.
Вместе они образуют <АОС=180
Значит <1+<2=180
Вывод: Сумма смежных углов равна
180

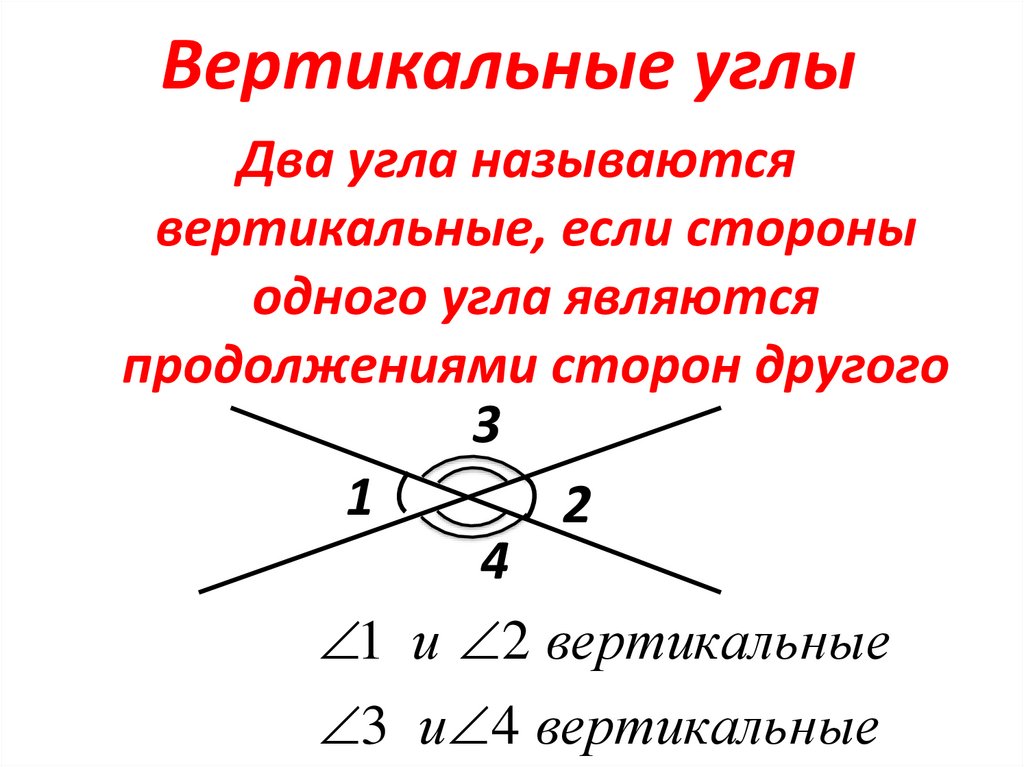
4. Вертикальные углы

Два угла называются
вертикальные, если стороны
одного угла являются
продолжениями сторон другого
3
1
2
4
1 и 2 вертикальные
3 и 4 вертикальные

5.

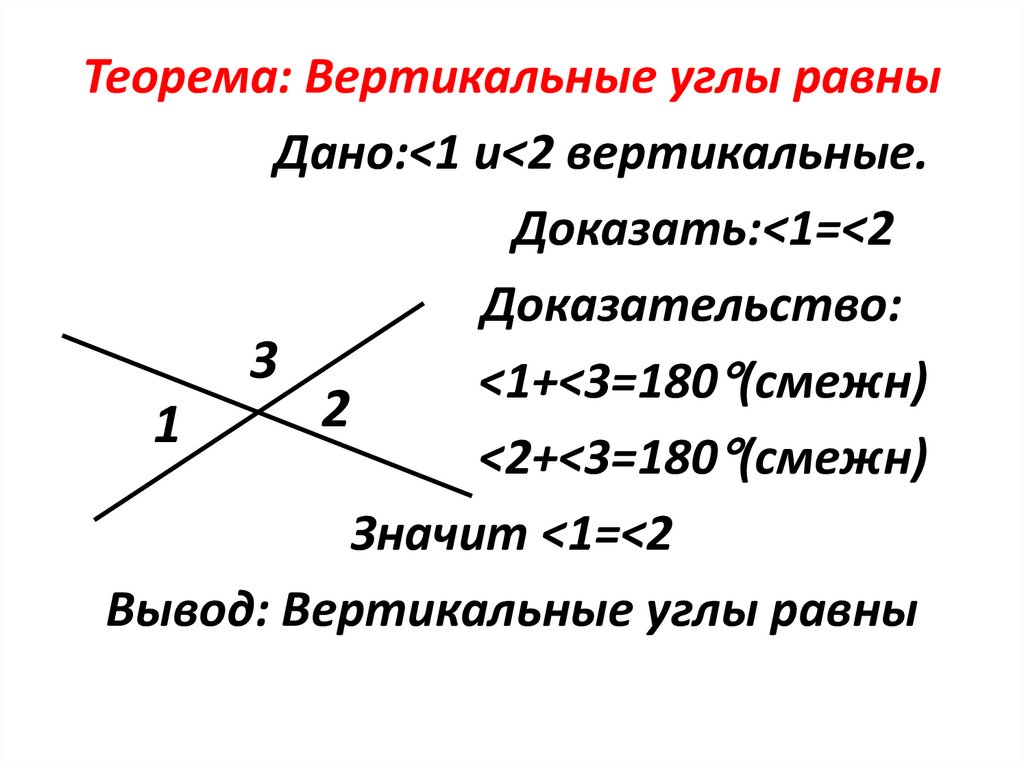
Теорема: Вертикальные углы равны
Дано:<1 и<2 вертикальные.
Доказать:<1=<2
Доказательство:
3
<1+<3=180 (смежн)
2
1
<2+<3=180 (смежн)
Значит <1=<2
Вывод: Вертикальные углы равны

6.

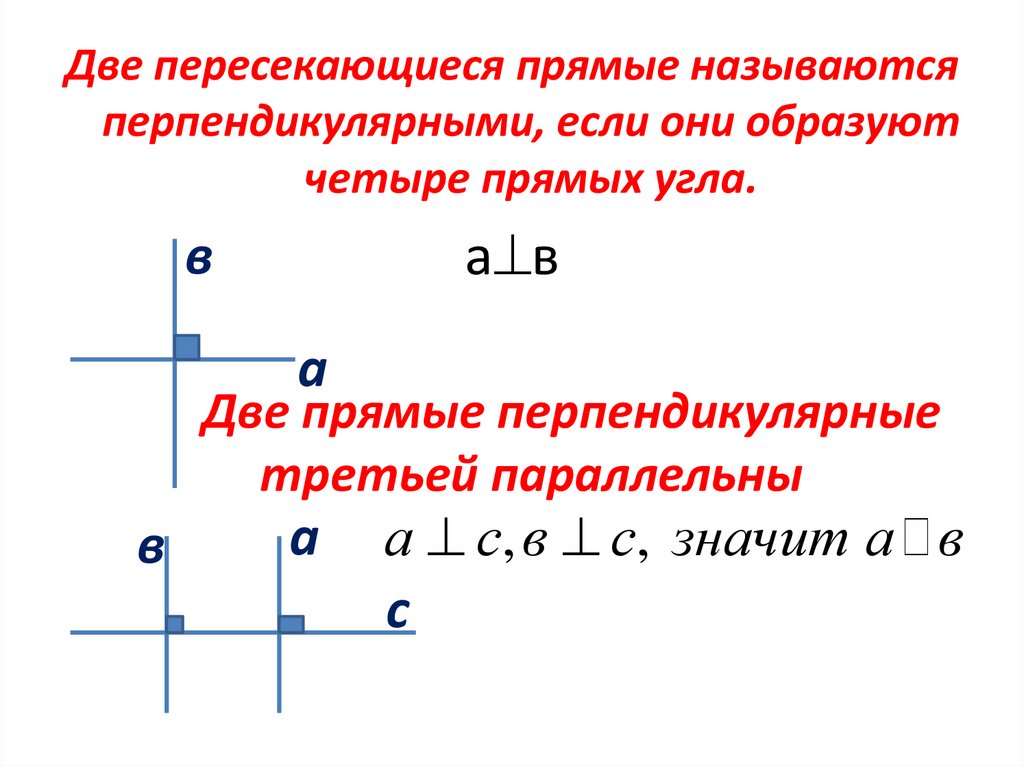
Две пересекающиеся прямые называются
перпендикулярными, если они образуют
четыре прямых угла.
а в
в
а
Две прямые перпендикулярные
третьей параллельны
в
а
а с, в с, значит а в
с

7. Решение задач

1) Один из смежных углов равен 30 . Чему равен
другой угол?
2)Разность смежных углов равна 30 . Чему равны
эти углы?
3)Один из смежных углов в 2 раза больше .
Найдите эти углы
4)Один из смежных углов на 30 больше. Найдите
эти углы.
5) Смежные углы относятся как 1:3. Найдите
эти углы.
6) Один из вертикальных углов 130 . Найдите
остальные три угла.