Similar presentations:
Оптимизация технологических и процессов общественного питания
1. Оптимизация технологических и процессов общественного питания
18 ч. Лекций, 36 ч. практических работ, 126 ч. cамостоятельной работы,экзамен
2. Оптимизация – поиск оптимума
Оптимумом, или оптимальным вариантом называется вариант, который являетсянаилучшим среди допустимых при наличии правила предпочтения одного другому.
Такое правило предпочтения называется критерием оптимальности.
Мера предпочтения – показатель качества (параметр оптимизации).
Основные подходы к оптимизации технологических процессов:
Бессистемно-случайный
Интуитивный
Интуитивно-логический
Научный (как правило, математический)
3. Литература
1. Разработка новых видов пищевых продуктов [Электронный ресурс] : метод. указания квыполнению практ. работы "Изучение методов оптимизации технологических режимов
основных технологических операций на этапе изготовления пищевой продукции" для студентов
направлений подгот. 100800.62 "Товароведение", 260200.62 "Продукты питания животного
происхождения" и специальности 080401.65 "Товароведение и экспертиза товаров в сфере
таможенной деятельности" / Федер. агентство по рыболовству, Мурман. гос. техн. ун-т, Каф.
технологий пищевых пр-в ; сост. Ю. В. Шокина. - Мурманск : Изд-во МГТУ, 2014
2. Глазунов, Ю. Т. Моделирование процессов пищевых производств : учеб. пособие для вузов / Ю.
Т. Глазунов, А. М. Ершов, М. А. Ершов ; Центр. учеб.-метод. каб. Гос. ком. РФ по рыболовству.
- Москва : Колос, 2008. - 358 с. : ил. - (Учебник). - Библиогр.: с. 341-343. - ISBN 978-5-10004018-7 : 293-00.
3. Алексеев, Г. В. Математические методы в пищевой инженерии: Учебное пособие / Г.В.
Алексеев, Б.А. Вороненко, Н.И. Лукин. – СПб. : Издательство «Лань», 2012. – 176 с.: ил.
4. Стефановский Н.В. и др. Процессы и аппараты рыбообрабатывающих производств. - М.; Легкая
и пищевая промышленность, 1984-236 стр.
5. Адлер, Ю. П. Планирование эксперимента при поиске оптимальных условий / Ю.П.Адлер [и
др.]. Изд. 2-е, перераб. и доп. - М.: Наука, 1976. – 280 с.
4. Классификация видов оптимизации
По количеству критериев (однокритериальная и многокритериальная)По наличию дополнительных условий (безусловная и условная)
По используемым математическим и/или вычислительным методам (линейное,
нелинейное программирование; метод крутого восхождения; методы нечёткой логики
и т.д.)
По способу получения целевой(ых) функции(ий) (методы планирования
экспериментов, методы регрессионного анализа, методы корреляционного анализа;
метод искусственных нейронных сетей; методы на основе анализа
дифференциальных уравнений; методы на основе теории подобия и др.)
5. Этапы оптимизации технологического процесса
1. Постановка задачи1.1. Определение параметров, подлежащих оптимизации и установление
ограничений
1.2. Поиск влияющих факторов
1.3. Выбор критерия оптимальности
2. Получение целевой функции (математической модели).
3.
Решение
задачи
оптимизации
математическими
и/или
вычислительными методами
4. Интерпретация результатов и распространение их на реальный объект
5. Оценка оптимальности полученных результатов.
6. Критерий оптимальности
Правильный выбор критерия оптимальности – это залог успеха всего процессаоптимизации.
Высокая субъективность выбора: ответ на вопрос «Что лучше»
Распространённый пример: соотношение «цена/качество»
Дополнительные условия при оптимизации (безопасность продукции и производства,
минимальный уровень качества или минимальная рентабельность и т.д.)
Показатели качества продукции: объективные и субъективные.
Выбор показателей (параметров) для критерия оптимальности
7. Требования к параметрам оптимизации
Простота определенияВысокая воспроизводимость
Очевидное направление оптимизации
Взаимосвязь с общей оценкой привлекательности продукции
(услуг)
8. Примеры параметров оптимизации
Общая рентабельность предприятия; окупаемость капитальных вложенийСебестоимость на единицу продукции или её часть
Показатели пищевой и биологической ценности (энергетическая ценность,
биологическая ценность белка, КЭБ, процент удовлетворения суточной потребности
и т.д.)
Уровень качества по органолептичекой оценке
Эстетические и эргономические показатели
Показатели, коррелирующие с вышеперечисленными
9. Примеры дополнительных условий оптимизации
Показатели безопасности (не выше допустимых норм с учётом запаса)Минимальная рентабельность предприятия/максимум капитальных вложений
Минимально-приемлемое качество по каждому органолептическому показателю
Предельные значения показателей назначения (массовая доля соли, сахара, влаги и
т.д.)
Минимальная или максимальная энергетическая ценность
Максимальные режимные параметры технологического процесса
Естественные пределы изменения параметров
10. Подходы к решению многопараметрических задач
Оптимизацияс
несколькими
целевыми
функциями
(многокритериальная оптимизация)
Замена некоторых параметров оптимизации дополнительными
условиями
Формирование единой целевой функции как линейной или
нелинейной комбинации от всех параметров оптимизации
Использование методов нечёткой логики для формирования условий
оптимальности.
11. Обобщённые параметры оптимизации
Уровень качества по органолептической оценке:Комплексный безразмерный показатель качества:
Аналогично при степенном подходе
12. Нормирование параметров
1. Изв
2. Из
в
3. Обратное преобразование:
4. Из
5. Из
в
в
в
13. Распространённые ошибки при выборе обобщённого параметра оптимизации
1. Отдельные параметры оптимизации не прошли нормирование и могут менятьсясовсем в другом диапазоне, тогда как коэффициенты значимости это не учитывают.
2. Один из параметров оптимизации имеет явный оптимум, который не был учтён, тогда
как остальные должны только возрастать или убывать.
3. Параметры, которые должны возрастать, складываются или умножаются на
параметры, которые должны убывать без учёта этого дополнительным
коэффициентом.
4. Два или более параметра связаны друг с другом (неоправданно увеличивается
значимость)
5. Ошибки выбора коэффициентов значимости
5.1. Коэффициенты значимости не выбираются, а условно принимаются равными
5.2.Сумма коэффициентов значимости маловажных параметров оказывается
неоправданно завышенной
5.3.Ошибки в нормировке максимального значения обобщённого параметра оптимизации
с помощью коэффициентов значимости
6. Обобщённым параметром оптимизации пытаются учесть и неприемлемый результат
по какому-то одному показателю (нейтрализуется другими)
14. Факторы
1. Варьируемые2. Фиксируемые
3. Неуправляемые
3.1. Управляемые пассивно
3.2. Совершенно неуправляемые
4. Не учитываемые
5. Не влияющие (маловлияющие)
15. Интервал варьирования факторов
Естественные границы варьированияНормирование уровней варьирования (-1; 0; +1)
Возможный выход за пределы варьирования.
16. Методы получения целевой функции
Анализ математических моделейИспользование теории подобия
Планирование эксперимента
Интерполяционные модели
Регрессионный и корреляционный анализ
Искусственные нейронные сети
Системы нечёткой логики
17. Моделирование технологических процессов
Натурное (эксперименты на реальном объекте)Физическое (на основе теории подобия)
Аналоговое (аналогичное) моделирование (используя процессы
другой природы)
Универсальное моделирование
(имитационные модели,
отражающие взаимосвязи реального объекта)
Математическое моделирование
18. Основы теории подобия
Подобие – это полная математическая аналогия при наличии пропорциональностимежду сходственными переменными, сохраняющаяся при всех возможных значениях
переменных
Два объекта являются подобными, если соотношение как геометрических, так и
физических величин между объектами одинаково.
Критерии подобия: симплексы (отношение одноимённых величин) и комплексы
(комбинация разноимённых величин)
Абсолютное подобие – у подобных процессов равны все критерии. На практике
встречается крайне редко (имеются несовместимые критерии даже при
геометрическом подобии)
Практическое
подобие
предполагает
подобие
только
определённых,
рассматриваемых свойств объекта. Может быть полным – подобие наблюдается в
пространстве и во времени, неполным (или в пространстве, или во времени),
приближённым (только в пределах допущений)
19. Теоремы подобия
Первая теорема (необходимое условие подобия) - для подобныхявлений существуют равные критерии подобия
Вторая теорема (π-теорема) - число критериев подобия равно
количеству всех размерных факторов за вычетом числа
основных единиц измерения, входящих в размерность факторов
Третья теорема – необходимыми и достаточными условиями
подобия
являются
пропорциональность
сходственных
параметров, входящих в условия однозначности, и равенство
критериев подобия
Получение математических моделей
на
основе
теории
подобия
1.Упрощение дифференциальных уравнений (опускаются знаки дифференцирования и
выделяются критерии подобия)
2.Метод анализа размерностей
20. Основы теории планирования эксперимента
Основная задача планирования эксперимента – минимизацияколичества
опытов
для
получения
максимальной
информации об объекте.
Для анализа линейных и близких к линейным зависимостей
достаточно двух уровней варьирования факторов –
эксперимент вида 2n (n – число факторов)
Уровни варьирования факторов нормируются до -1 … +1
(иногда обозначают «–» и «+»).
Однофакторное планирование – 21: -1 +1.
21. Полный факторный эксперимент 2n
X1X2
+1
+1
-1
+1
+1
-1
-1
-1
Y
Х1
Х2
Х3
+1
-1
+1
-1
+1
-1
+1
-1
+1
+1
-1
-1
+1
+1
-1
-1
+1
+1
+1
+1
-1
-1
-1
-1
Y
22. Дробный факторный эксперимент
Рост числа влияющих факторов приводит к экспоненциальному росту числа опытовПФЭ позволяет получить (без учёта оценки погрешности) линейную модель с
эффектами взаимодействий. Например, по плану 22 можно получить уравнение
y a bX1 cX 2 dX1 X 2
(так как имеется 4 уравнения, то можно определить 4 неизвестных коэффициента,
хотя для регрессии требуется хотя бы одна степень свободы)
Если есть основания полагать, что эффекты взаимодействия отсутствуют, т.е.
факторы влияют на параметр оптимизации линейно и независимо, то один из опытов
в плане «лишний», и его можно опустить. Для эксперимента 22 это редко бывает
актуальным, т.к. 4 опыта вполне можно провести, а «экономия» составляет всего
лишь 1 опыт. Для плана 23 уравнение будет иметь вид
Y a bX 1 cX 2 dX 3 eX 1 X 2 fX 2 X 3 gX 1 X 3 hX 1 X 2 X 3
(т.е. на 8 опытов приходится 8 коэффициентов).
Если же опустить все эффекты взаимодействия, то получится всего лишь 4 опыта. Их
называют «полурепликой» 23-1
23. Полуреплика 23-1
Х1Х2
Х3
+1
-1
+1
-1
+1
-1
-1
+1
+1
+1
-1
-1
Y
Фактически, здесь X3 выбирается как эффект взаимодействия для
ПФЭ 22: Х1Х2.
24. Планы Плакетта-Бермана
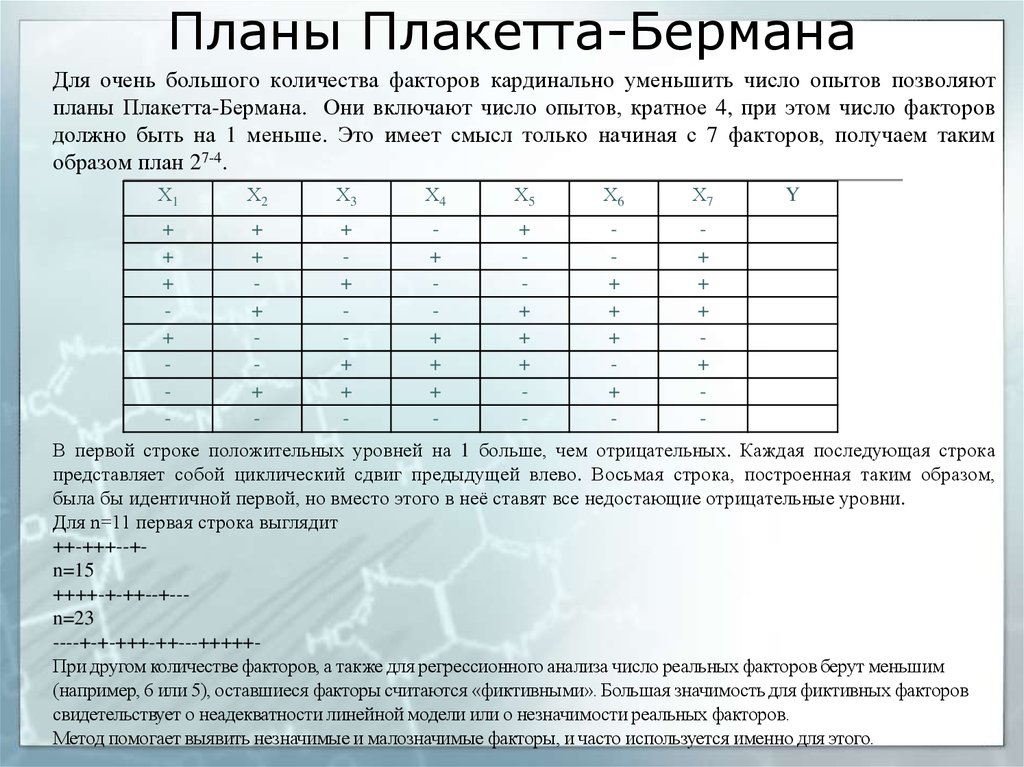
Для очень большого количества факторов кардинально уменьшить число опытов позволяютпланы Плакетта-Бермана. Они включают число опытов, кратное 4, при этом число факторов
должно быть на 1 меньше. Это имеет смысл только начиная с 7 факторов, получаем таким
образом план 27-4.
Х1
Х2
Х3
Х4
Х5
Х6
Х7
+
+
+
+
-
+
+
+
+
-
+
+
+
+
-
+
+
+
+
-
+
+
+
+
-
+
+
+
+
-
+
+
+
+
-
Y
В первой строке положительных уровней на 1 больше, чем отрицательных. Каждая последующая строка
представляет собой циклический сдвиг предыдущей влево. Восьмая строка, построенная таким образом,
была бы идентичной первой, но вместо этого в неё ставят все недостающие отрицательные уровни.
Для n=11 первая строка выглядит
++-+++--+n=15
++++-+-++--+--n=23
----+-+-+++-++---+++++При другом количестве факторов, а также для регрессионного анализа число реальных факторов берут меньшим
(например, 6 или 5), оставшиеся факторы считаются «фиктивными». Большая значимость для фиктивных факторов
свидетельствует о неадекватности линейной модели или о незначимости реальных факторов.
Метод помогает выявить незначимые и малозначимые факторы, и часто используется именно для этого.
25. Композиционные планы
Дробные и полные планы эксперимента с двумя уровнями варьирования позволяют работать слинейными зависимостями, при учёте эффектов взаимодействия допускается некоторая
нелинейность.
Вблизи экстремума даже ПФЭ 2n не позволяет изучить поверхность отклика (график целевой
функции) и, как следствие, не подходит для решения задач оптимизации.
В случае, если имеются основания предполагать наличие экстремума в пределах варьирования
факторов, следует применять композиционные планы, включающие ПФЭ и «звёздные» точки –
точки, находящиеся на осях плана и отстоящих от него на определённую величину – плечо (γ).
Кроме того, в состав многих композиционных планов вводят одну или несколько точек в центре
плана.
Если факторы симметричны относительно центра плана, то такой план называют центральным
композиционным планом (ЦКП).
К ЦКП часто предъявляют требования ортогональности (сумма произведений элементов
матрицы планирования равна нулю). В этом случае плечо звёздных точек можно принять 1, т.е.
звёздные точки будут в середине боковых сторон (граней, гиперграней) квадрата (куба,
гиперкуба).
Для большей адекватности модели чаще всего пользуются рототабельным ЦКП, в котором
звёздные точки можно получить поворотом ПФЭ относительно центра на определённый угол.
26. Геометрическая интерпретация ЦКП для ПФЭ 22
ПФЭЦОКП
ЦРКП
27. Центральный рототабельный план 22
Х1Х2
+1
+1
-1
+1
+1
-1
-1
-1
-1,414 0
+1,414 0
0 -1,414
0 +1,414
0
0
Y
28. Центральный рототабельный план 23
Х1Х2
Х3
+1
+1
+1
-1
+1
+1
+1
-1
+1
-1
-1
+1
+1
+1
-1
-1
+1
-1
+1
-1
-1
-1
-1
-1
-1,732 0
0
+1,732 0
0
0 -1,732 0
0 +1,732 0
0
0 -1,732
0
0 +1,732
0
0
0
Y
29. Особенности практического использования теории планирования эксперимента
Необходимость учёта ошибки опытов – повторныеэксперименты (особенно в центре плана)
Систематическая ошибка, связанная с последовательностью
опытов – переводится в случайную рандомизацией.
Необходимость получить несколько степеней свободы для
регрессионного анализа
Правильное нормирование факторов (с учётом запаса на
«звёздные точки»)
Возможность многократного планирования с последующим
движением методом «крутого восхождения»
30. Рандомизация
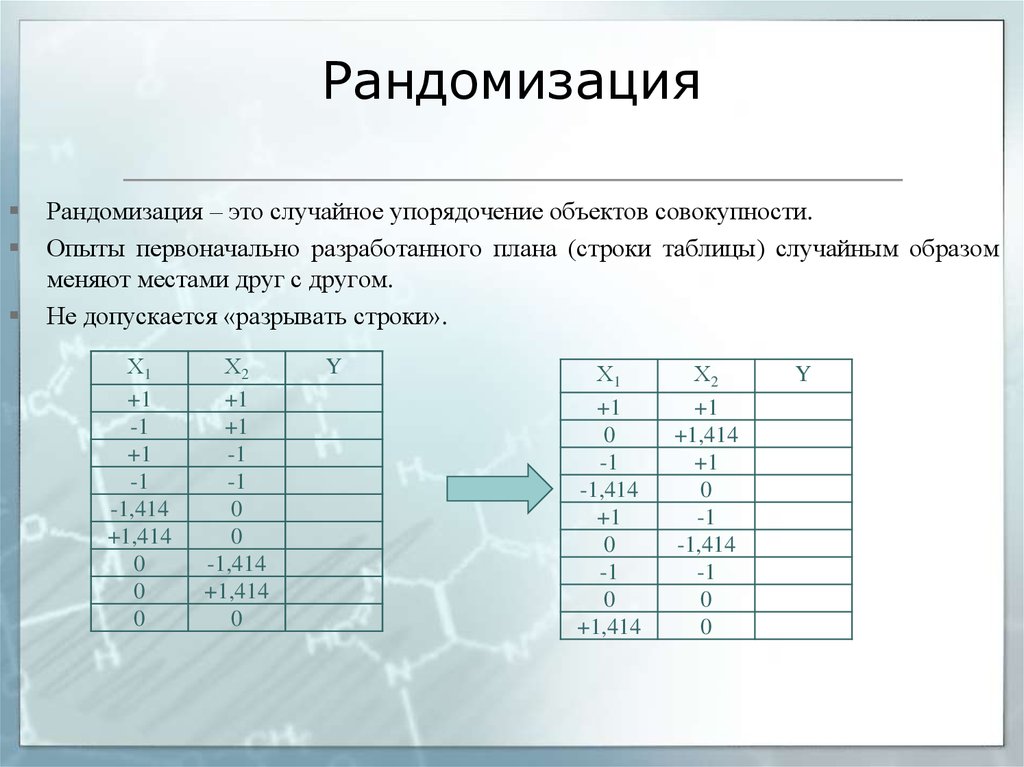
Рандомизация – это случайное упорядочение объектов совокупности.Опыты первоначально разработанного плана (строки таблицы) случайным образом
меняют местами друг с другом.
Не допускается «разрывать строки».
Х1
+1
-1
+1
-1
-1,414
+1,414
0
0
0
Х2
+1
+1
-1
-1
0
0
-1,414
+1,414
0
Y
Х1
+1
0
-1
-1,414
+1
0
-1
0
+1,414
Х2
+1
+1,414
+1
0
-1
-1,414
-1
0
0
Y
31. Предварительная обработка экспериментальных данных
1. Обработка результатов повторяющихся опытов2. Обработка «временных рядов» и последовательных экспериментов
2.1. Сглаживание
2.2. Интерполяция
3. Работа с разнородными выборками
3.1. Дисперсионный анализ
3.2. Корреляционный анализ
32. Сглаживание экспериментальных данных
Графический интуитивный методРегрессионные методы (МНК)
Упрощённые методы сглаживания
1
yi* ( yi 1 yi yi 1 )
3
(кроме первой и последней точек)
33. Интерполяция и интерполяционные модели
Интерполяция – способ получения промежуточных данных по имеющимся точкамВ большинстве случаев методы интерполяции не проходят статистического
обоснования.
Методы интерполяции
Метод ближайшего соседа
Линейная интерполяция
Полиномиальная интерполяция (формулы Ньютона, Лагранжа, сплайн-интерполяция
и т.д.)
Достоинства полиномиальной интерполяции:
Позволяет получить гладкую функцию
Не требует сложных статистических обоснований
Недостатки полиномиальной интерполяции:
Есть риск получить экстремум при отсутствии предпосылок к нему
Неэффективна при значительной случайной ошибке опытов
34. Дисперсионный анализ
Позволяет оценить, влияет ли фактор на параметр оптимизацииИспользует F-распределение (критерий Фишера)
Многофакторный дисперсионный анализ позволяет оценить эффекты взаимодействия
Термины, определения, обозначения
xi,j – единичное измерение в группе (выборке) i, имеющее порядковый номер j
M – математическое ожидание генеральной совокупности, равное среднему
арифметическому. Мi – математическое ожидание i-й выборки (равное среднему
арифметическому выборки).
SS – сумма квадратов отклонений. SSi=(xi,j –Mi) для i-й выборки (внутригрупповая сумма
квадратов отклонений, SSWG)
Выделяют общую сумму квадратов отклонений, SSt, внутригрупповую SSWG и
межгрупповую SSBG (связанную с различием математических ожиданий)
D – дисперсия (иногда обозначается MS). Равна сумме квадратов отклонений, делённому
на число степеней свободы.
F – критерий Фишера. Равен отношению двух дисперсий.
35. Последовательность однофакторного дисперсионного анализа
Выбирается несколько выборок данных (не менее 2), различающихся значениемфактора
В каждой выборке определяют сумму квадратов SSWG
Нулевая гипотеза – все мат.ожидания равны (М=М1=М2=…)
Проверка гипотезы:
SS
D
где J – число групп (выборок) J 1
BG
BG
DW G
SSW G
N J
где N – объём полной выборки (общее число опытов)
F
DBG
DW G
Рассчитанный критерий Фишера сравнивают с табличным, если он больше, то
нулевую гипотезу отвергают с доверительной вероятностью. В противном случае
нельзя исключить, что фактор не влияет на параметр оптимизации, такие факторы
называют незначимыми или малозначимыми. Для более точного результата следует
повторить анализ с большими объемами выборок и количеством групп.
36. Многофакторный дисперсионный анализ
Предполагает наличие нескольких факторов: A, B, С и т.д.Дополнительно вводятся суммы квадратов










































































 industry
industry








