Similar presentations:
Касательная к окружности, ее свойства
1.
Тема урока:Касательная к окружности,
ее свойства.
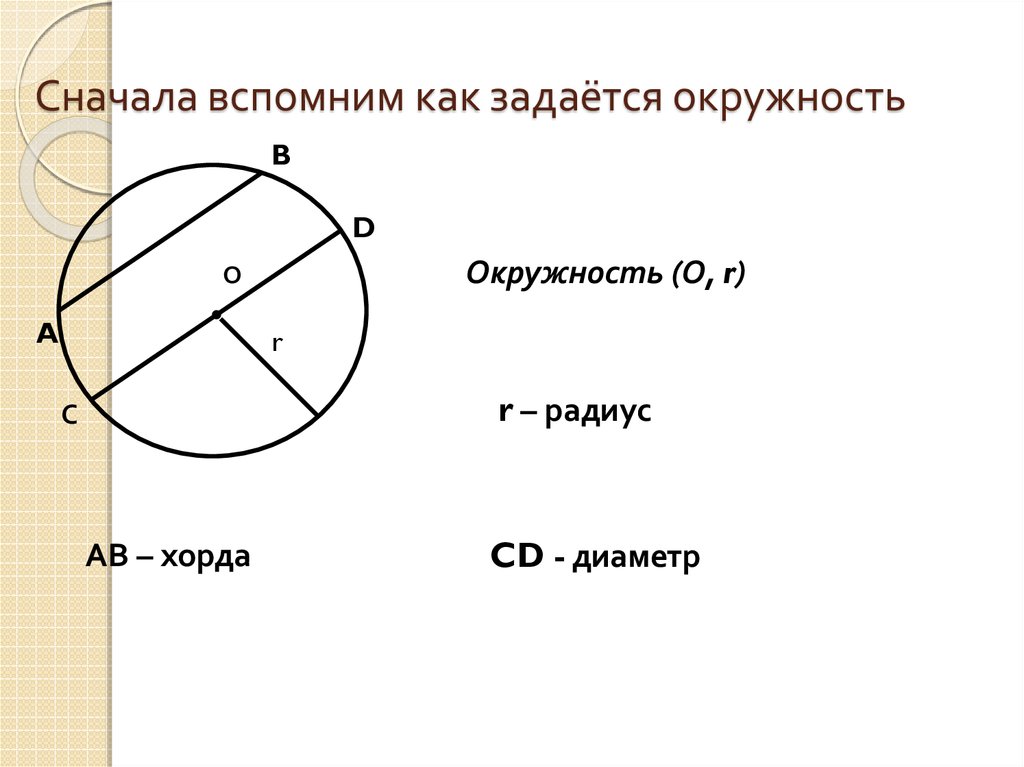
2. Сначала вспомним как задаётся окружность
BD
Окружность (О, r)
О
A
r
r – радиус
С
АВ – хорда
CD - диаметр
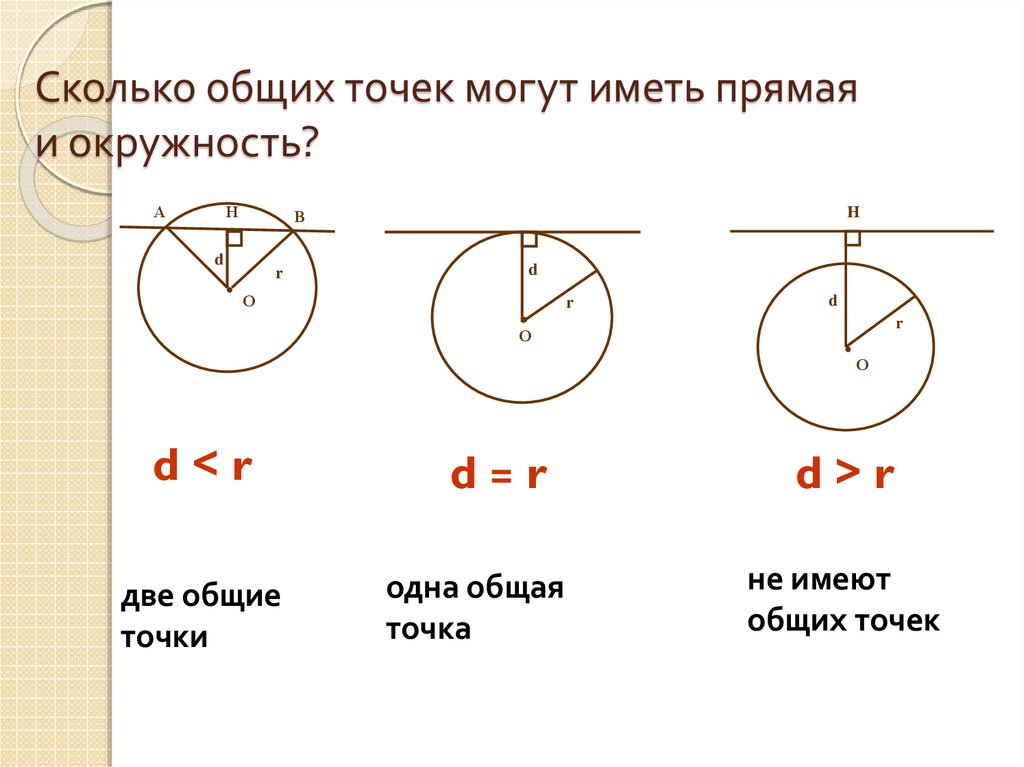
3. Сколько общих точек могут иметь прямая и окружность?
АН
H
В
d
r
d
О
r
d
r
О
О
d<r
две общие
точки
d=r
одна общая
точка
d>r
не имеют
общих точек
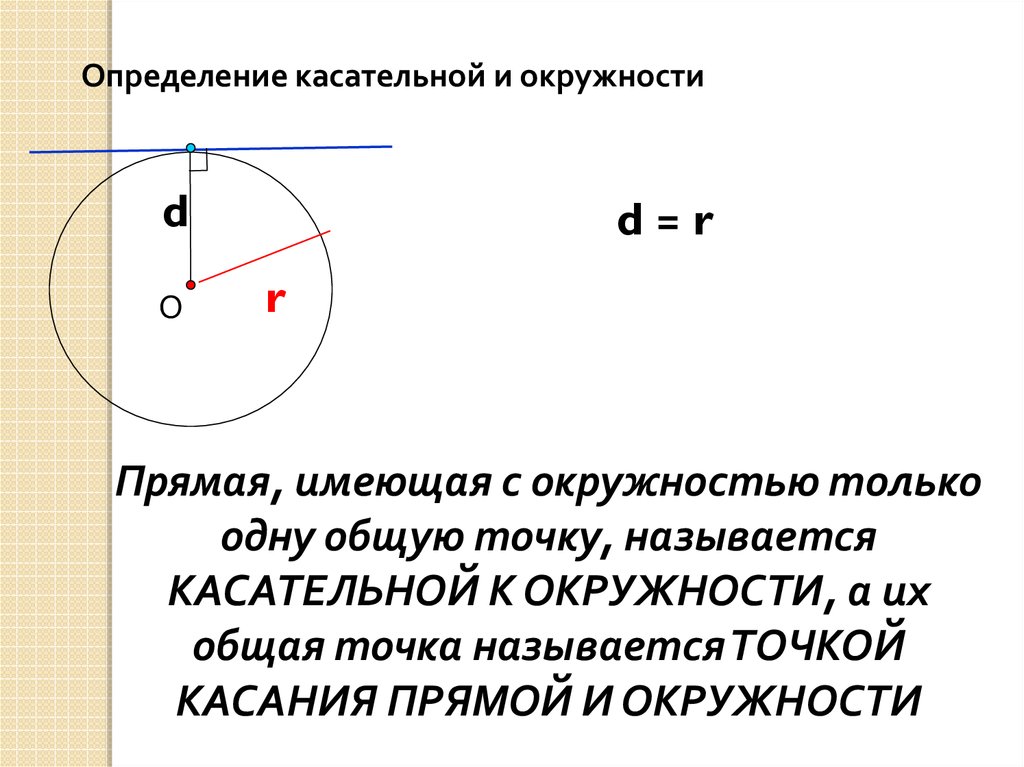
4.
Определение касательной и окружностиd
О
d=r
r
Прямая, имеющая с окружностью только
одну общую точку, называется
КАСАТЕЛЬНОЙ К ОКРУЖНОСТИ, а их
общая точка называется ТОЧКОЙ
КАСАНИЯ ПРЯМОЙ И ОКРУЖНОСТИ
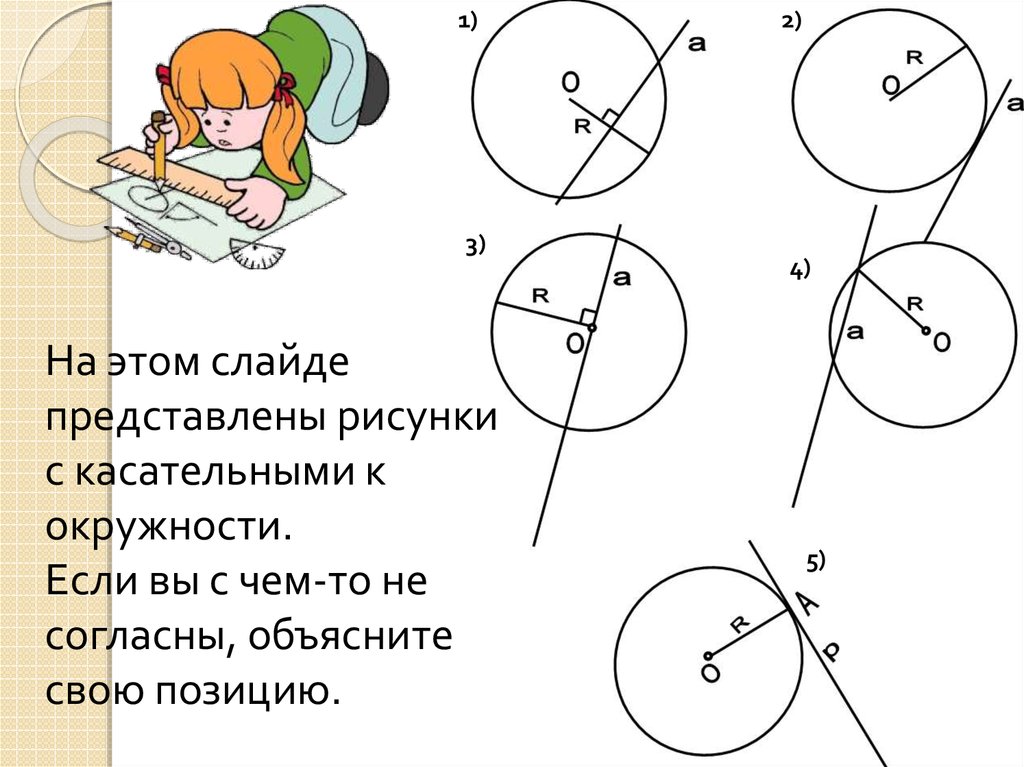
5.
1)3)
На этом слайде
представлены рисунки
с касательными к
окружности.
Если вы с чем-то не
согласны, объясните
свою позицию.
2)
4)
5)
6.
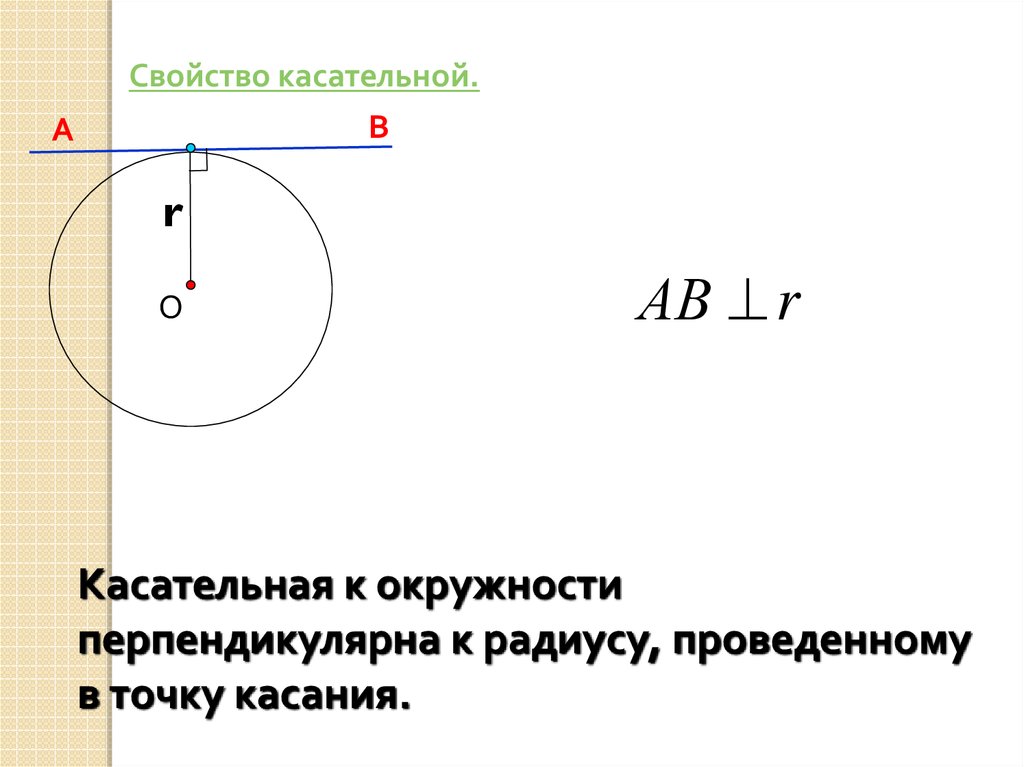
АСвойство касательной.
В
r
О
АВ r
Касательная к окружности
перпендикулярна к радиусу, проведенному
в точку касания.
7.
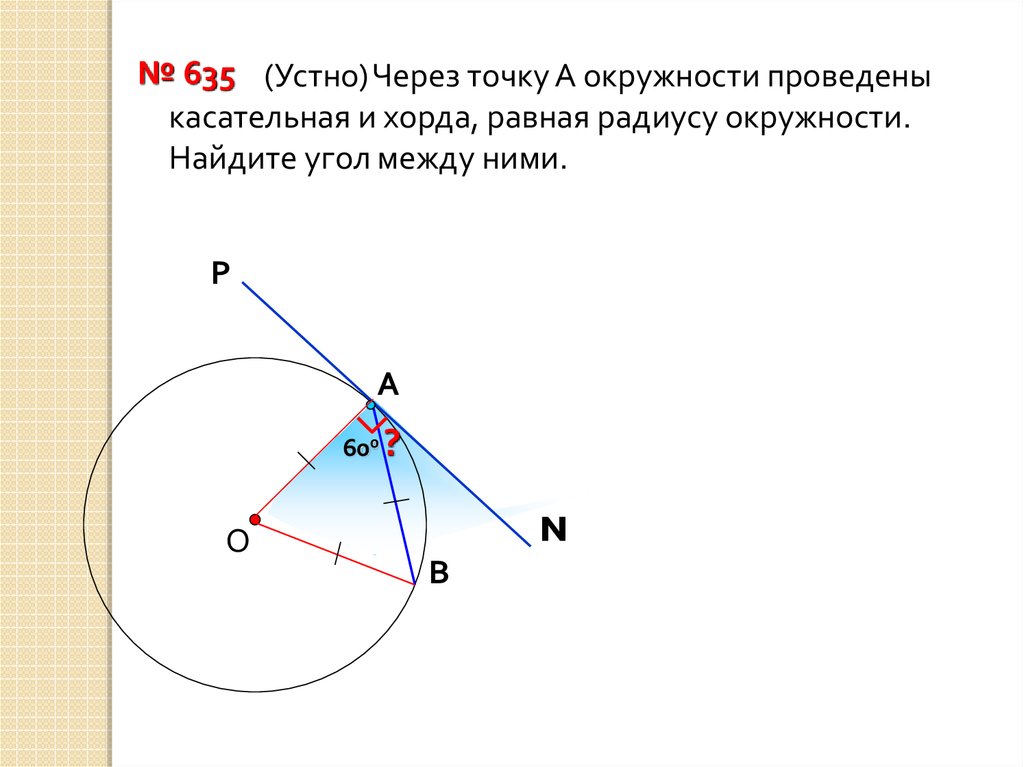
№ 635 (Устно) Через точку А окружности проведеныкасательная и хорда, равная радиусу окружности.
Найдите угол между ними.
Р
А
600 ?
О
N
В
8.
№ 636 (самостоятельно). Через концы хорды АВ, равнойрадиусу окружности, проведены две касательные,
пересекающиеся в точке С. Найдите угол АСВ.
А
600
?
О
600
В
С
9.
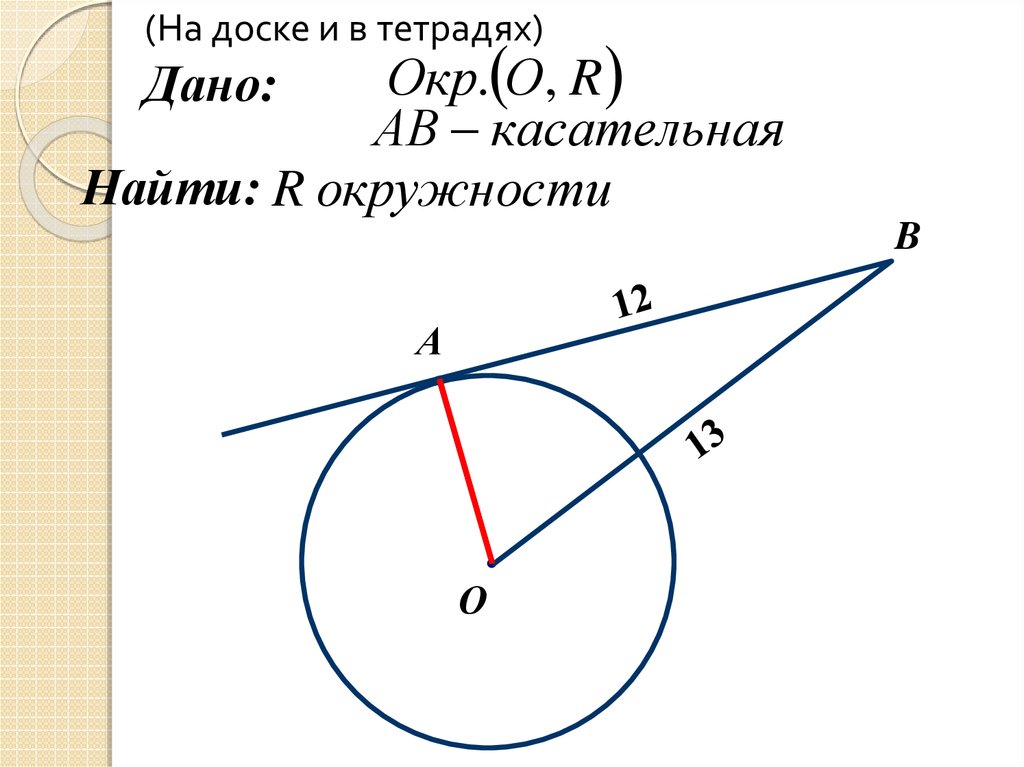
(На доске и в тетрадях)Окр. О , R
АВ касательная
Найти: R окружности
Дано:
B
А
О
10.
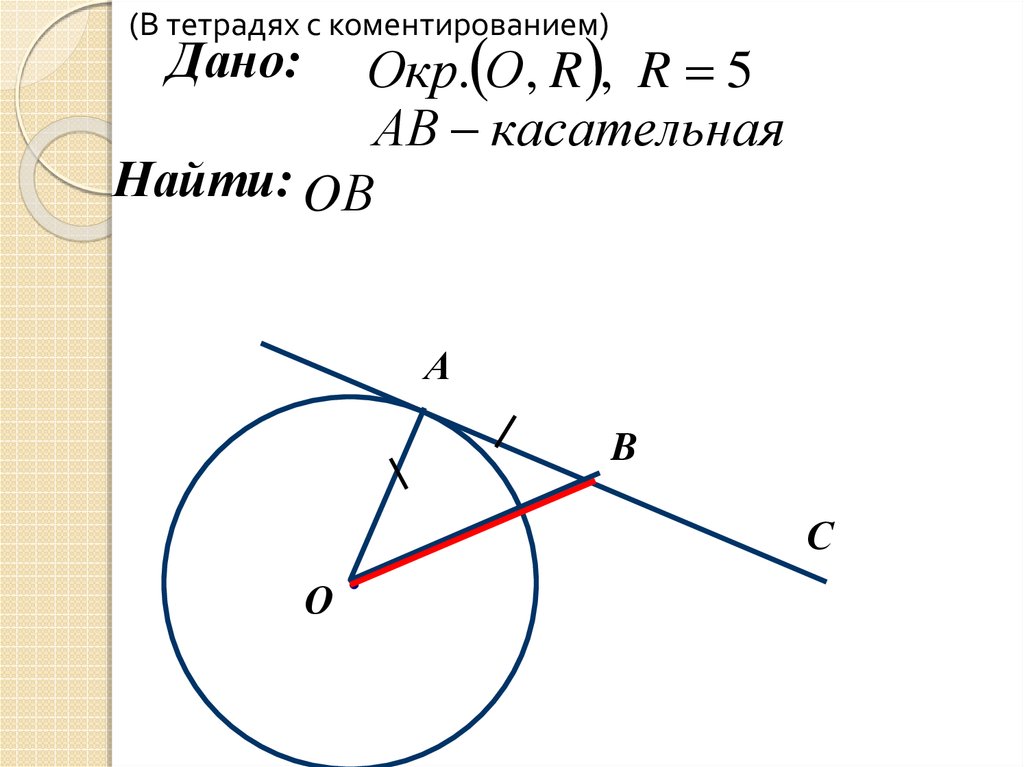
(В тетрадях с коментированием)Окр. О , R , R 5
АВ касательная
Найти: OВ
Дано:
А
B
С
О
11.
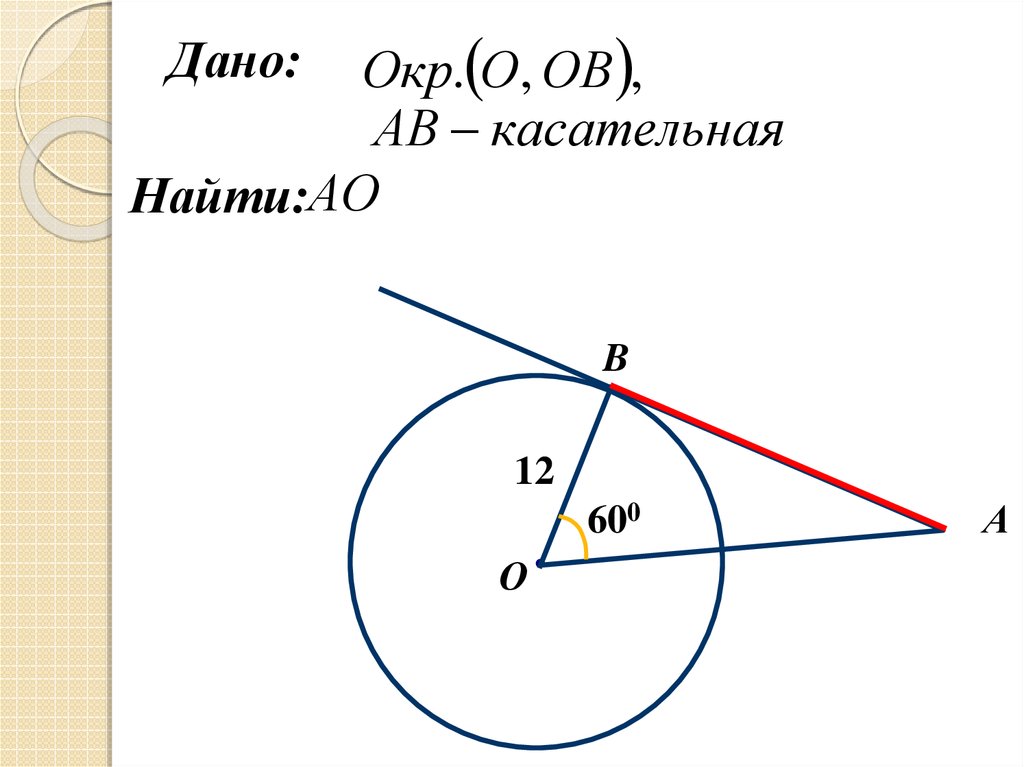
Окр. О , ОВ ,АВ касательная
Найти:АО
Дано:
B
12
600
О
А
12.
отрезки касательных,проведенных из точки А
А
3
B
Теорема: ОТРЕЗКИ КАСАТЕЛЬНЫХ К
4
ОКРУЖНОСТИ, ПРОВЕДЕННЫЕ ИЗ
ОДНОЙ ТОЧКИ, РАВНЫ И
СОСТАВЛЯЮТ РАВНЫЕ УГЛЫ С
2
1
О
ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ЭТУ
ТОЧКУ И ЦЕНТР ОКРУЖНОСТИ
C
ABO ACO
(ОА – общая, ОВ = ОС)
AВ = АС
3 4
13.
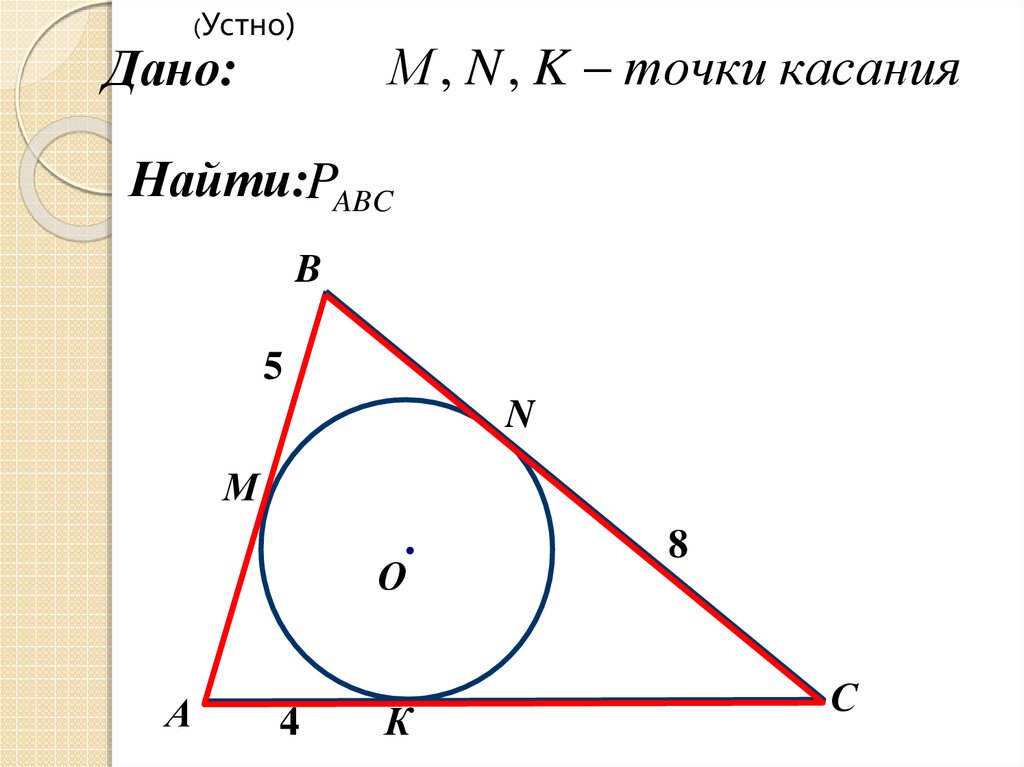
(Устно)М , N , K точки касания
Дано:
Найти:PABC
B
5
N
М
О
А
4
К
8
С
14.
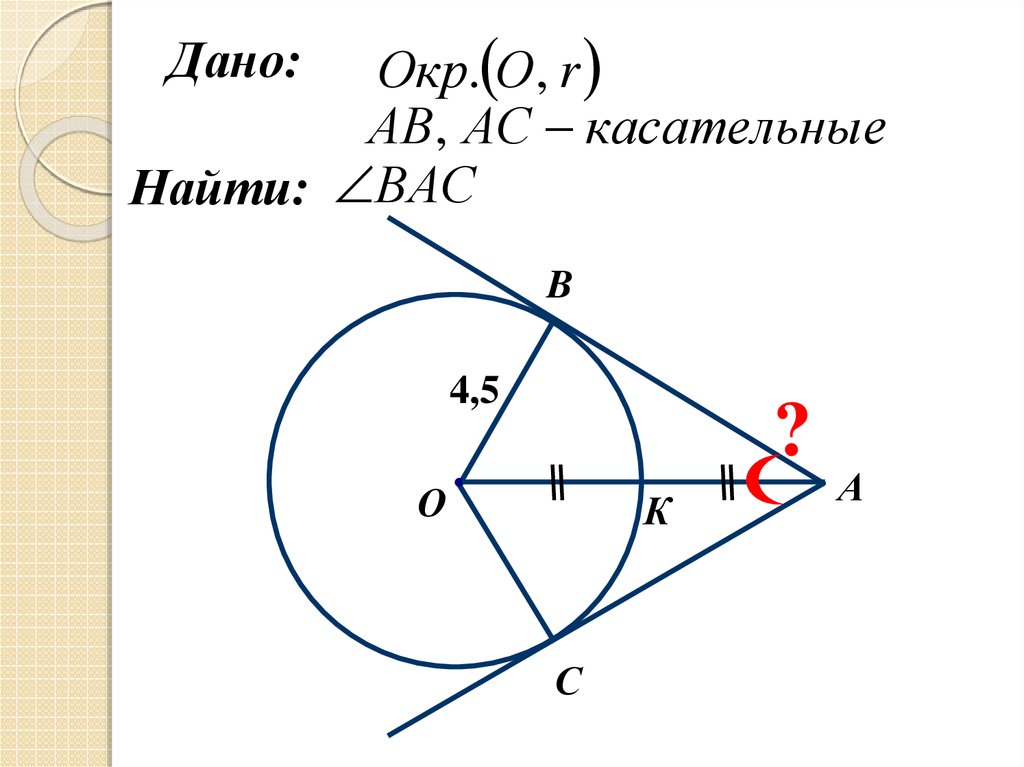
Окр. О , rАВ, АС касательные
Найти: ВАС
Дано:
B
4,5
?
О
К
С
А
15.
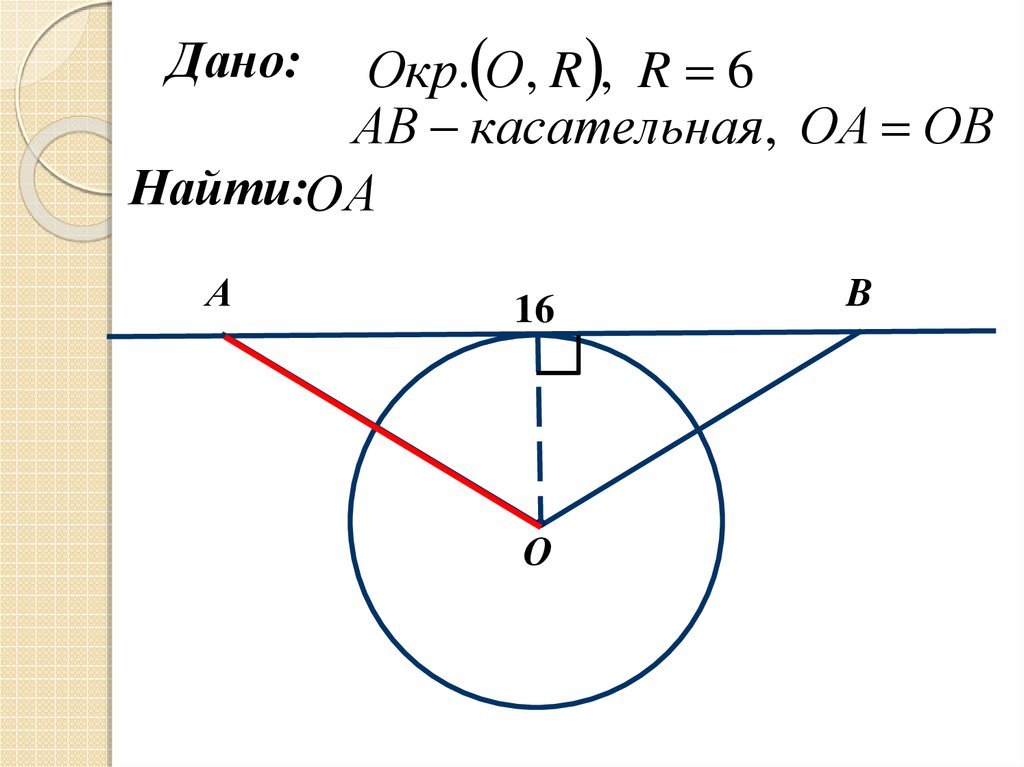
Окр. О , R , R 6АВ касательная, ОА ОВ
Найти:OА
Дано:
А
16
О
B
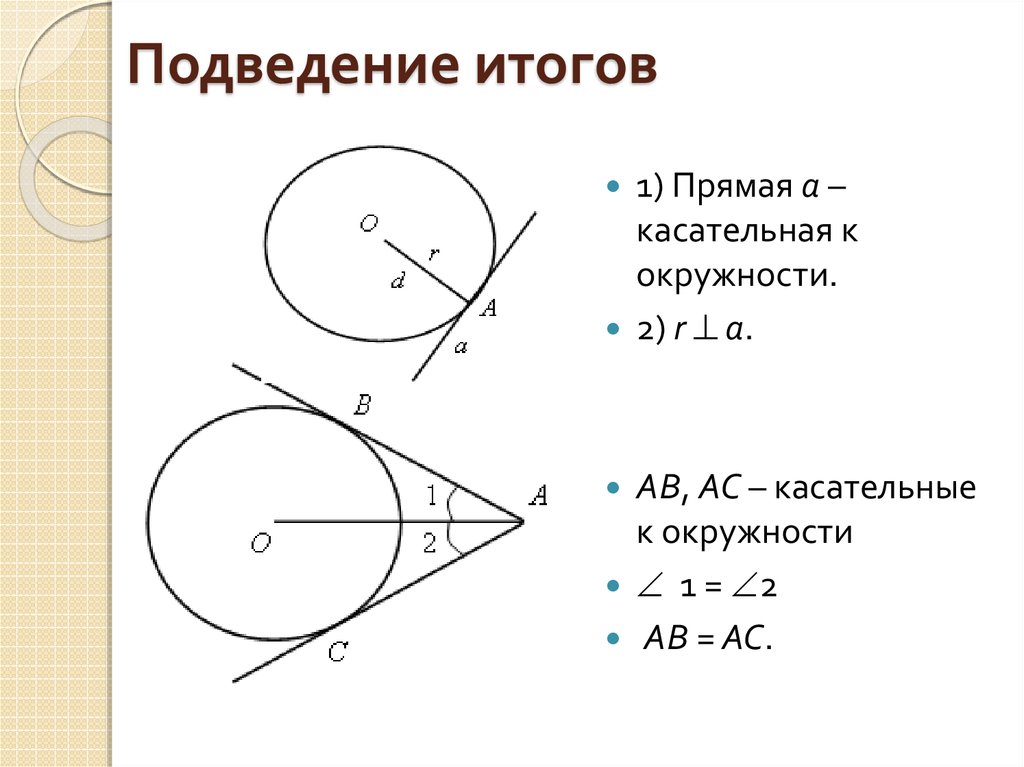
16. Подведение итогов
1) Прямая а –касательная к
окружности.
2) r a.
АВ, АС – касательные
к окружности
1 = 2
АВ = АС.




 mathematics
mathematics








