Центральная симметрия

1.

2.

Определение
Термин «симметрия» (от греч. Symmetria ) соразмерность, пропорциональность, одинаковость
в расположении частей.

3.

Две точки А и В называются симметричными
относительно точки О, если О - середина
отрезка АВ. Точка О считается симметричной
самой себе.
А
В

4. Построение точки, центрально-симметричной данной

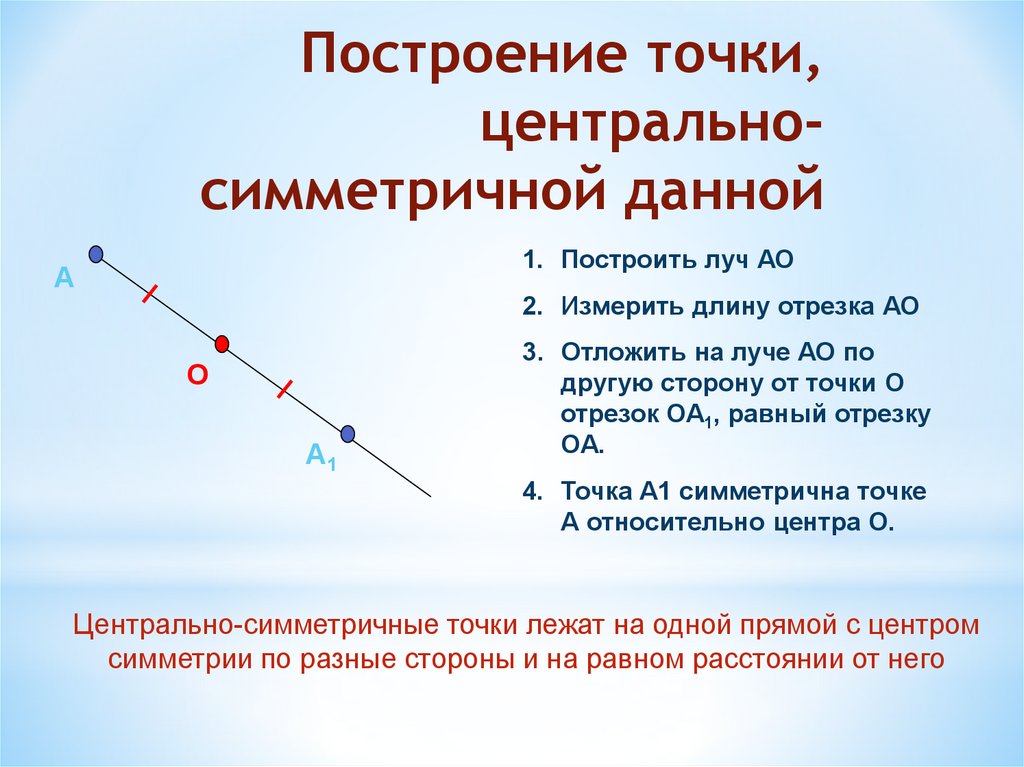
Построение точки,
центральносимметричной данной
1. Построить луч АО
А
2. Измерить длину отрезка АО
О
А1
3. Отложить на луче АО по
другую сторону от точки О
отрезок ОА1, равный отрезку
ОА.
4. Точка А1 симметрична точке
А относительно центра О.
Центрально-симметричные точки лежат на одной прямой с центром
симметрии по разные стороны и на равном расстоянии от него

5. Построение отрезка, центрально-симметричного данному

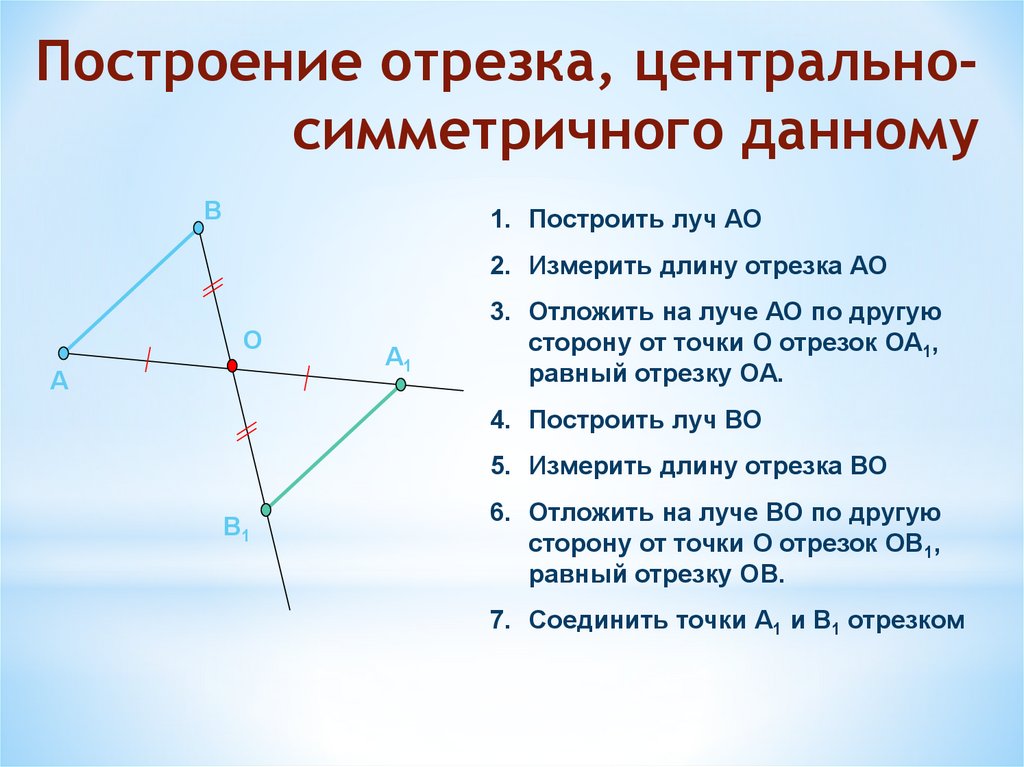
Построение отрезка, центральносимметричного данному
В
1. Построить луч АО
2. Измерить длину отрезка АО
О
А
А1
3. Отложить на луче АО по другую
сторону от точки О отрезок ОА1,
равный отрезку ОА.
4. Построить луч ВО
5. Измерить длину отрезка ВО
В1
6. Отложить на луче ВО по другую
сторону от точки О отрезок ОВ1,
равный отрезку ОВ.
7. Соединить точки А1 и В1 отрезком

6. Построение фигуры, центрально-симметричной данной

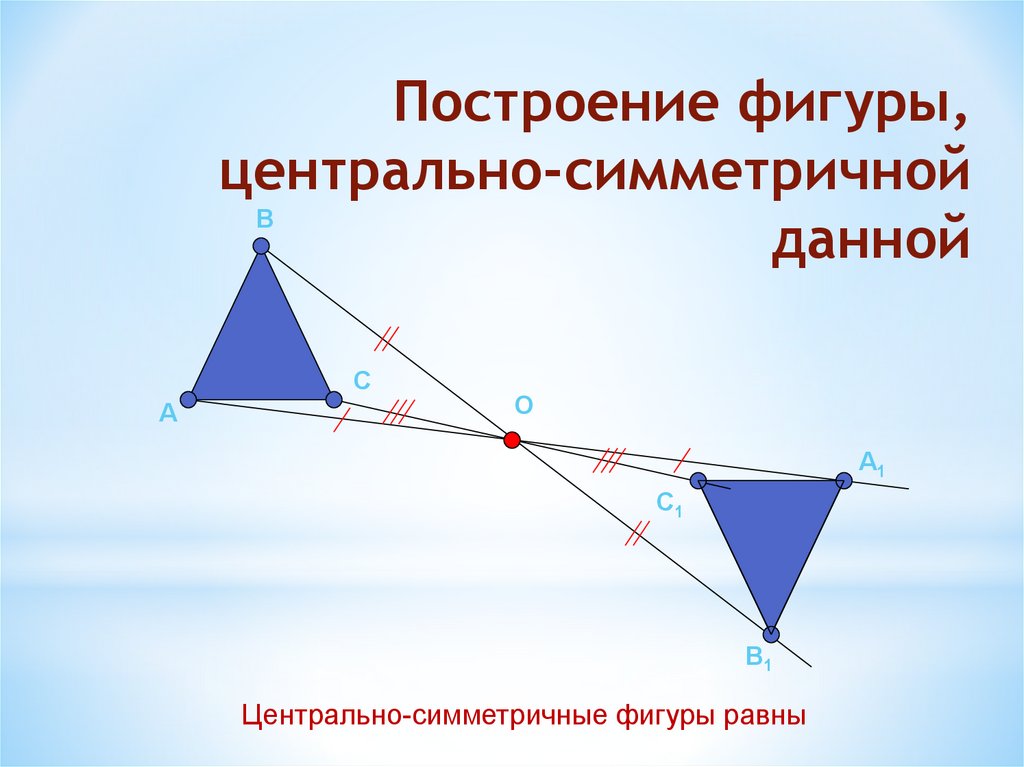
Построение фигуры,
центрально-симметричной
В
данной
С
А
О
А1
С1
В1
Центрально-симметричные фигуры равны

7. Фигуры, имеющие центр симметрии:

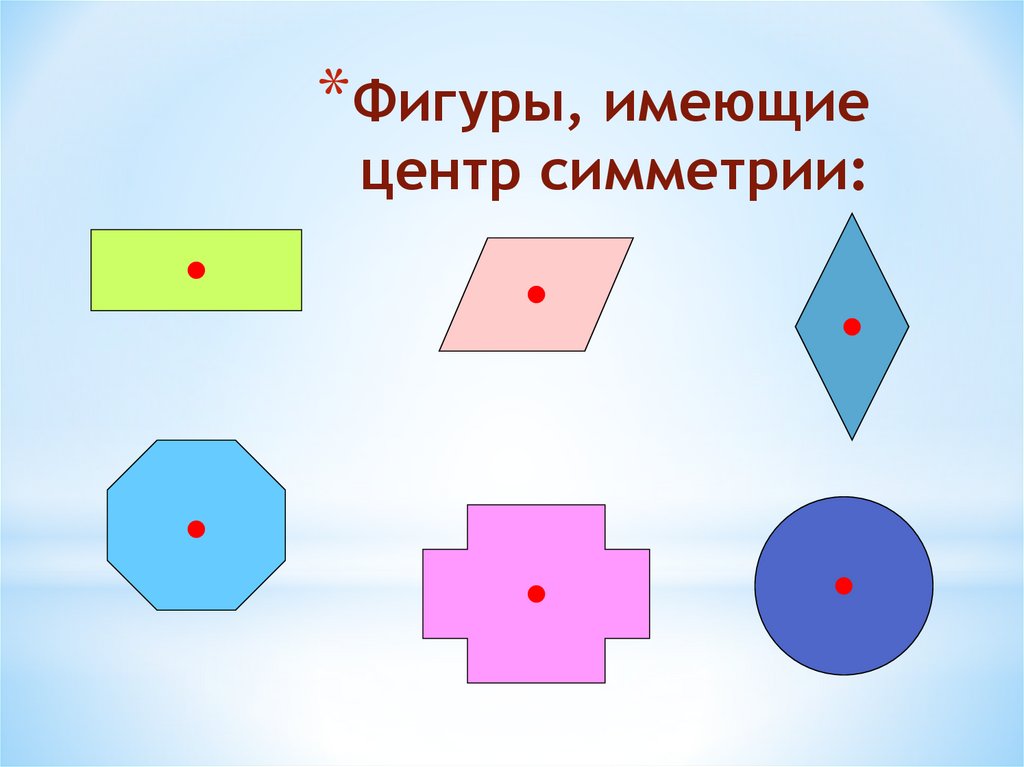
*Фигуры, имеющие
центр симметрии:

8. Центральная симметрия

9.

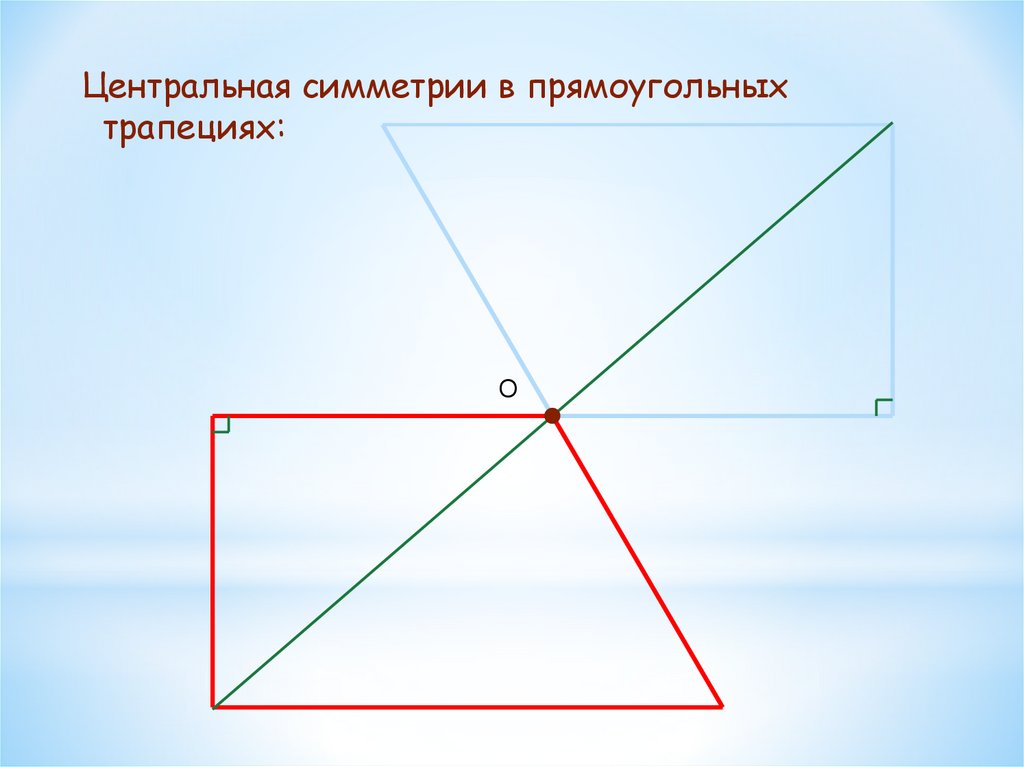
Центральная симметрии в прямоугольных
трапециях:
О

10.

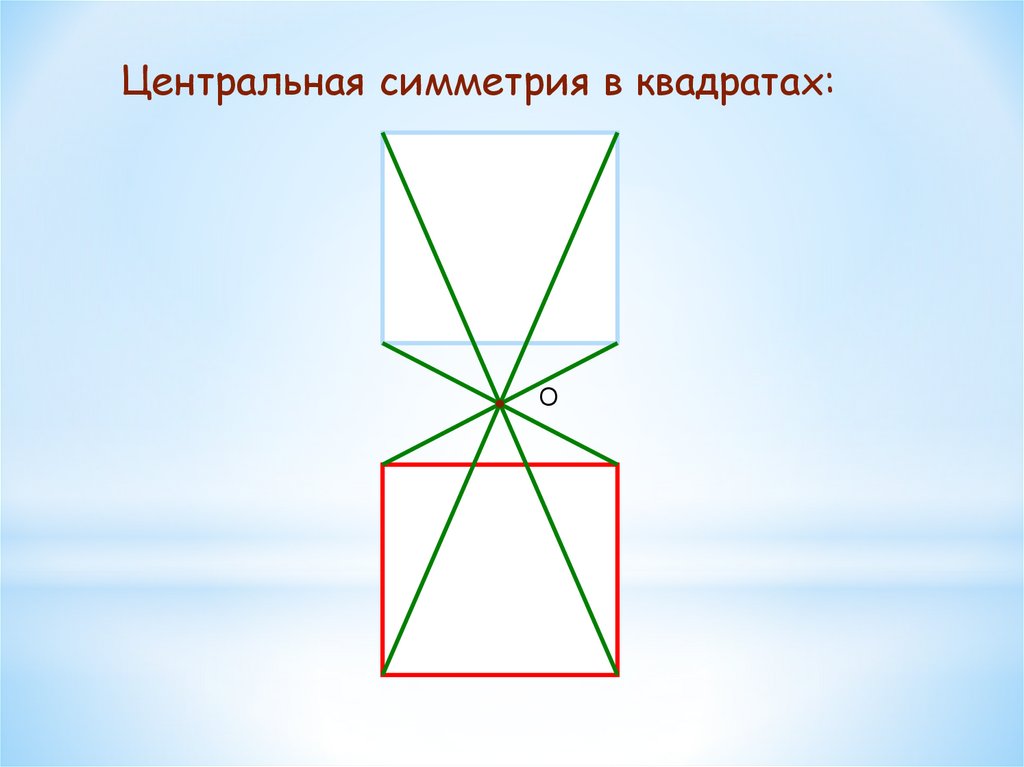
Центральная симметрия в квадратах:
О

11.

Центральная симметрия в
параллелограммах:
О

12.

Центральная симметрия в шестиконечной
звезде:
О

13.

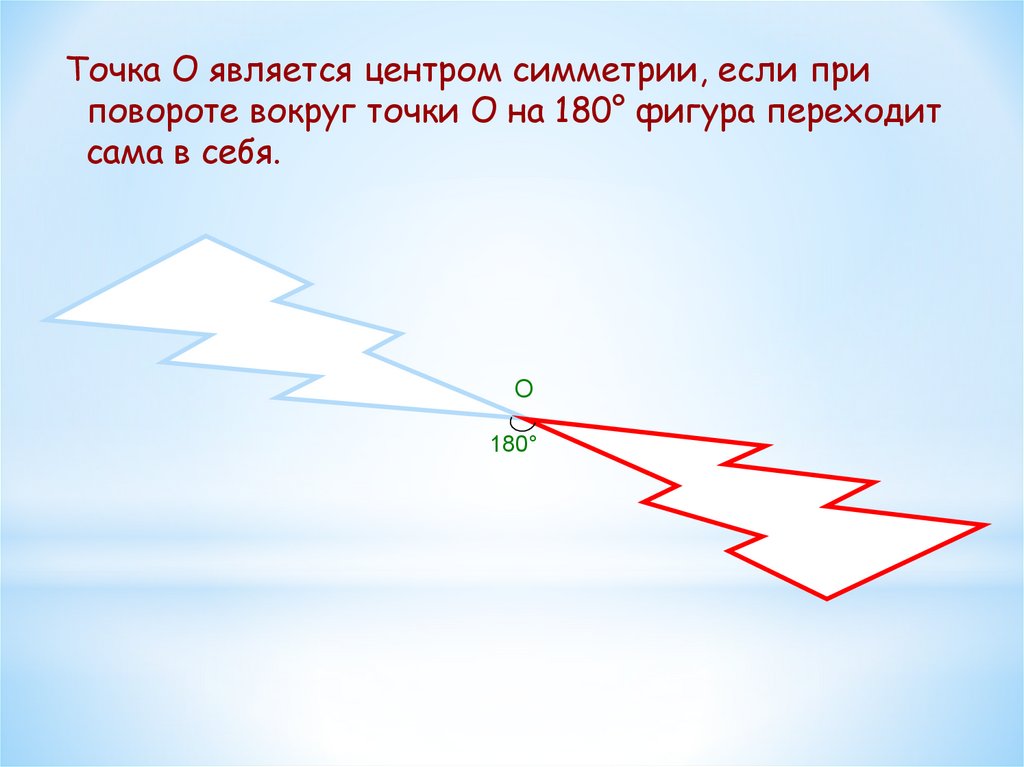
Точка О является центром симметрии, если при
повороте вокруг точки О на 180° фигура переходит
сама в себя.
О
180°

14. Где встречается центральная симметрия?

15. В природе

16. В искусстве, архитектуре и быту

17. В работах учеников