Энтропия. Тепловые двигатели. (Лекция 10)

1.

Лекция № 10
Энтропия. Тепловые двигатели.
План лекции.
10.1. Макро – и микросостояния макроскопической системы. Статистический вес
макросостояния и вероятность макросостояния. Статистический вес различных мак –
росостояний (на примере распределения молекул по половинкам сосуда). Мульти –
пликативность статистического веса.
10.2. Энтропия и ее свойства. Второе начало термодинамики. Третье начало термо –
динамики (теорема Нернста).
10.3. Равенство Клаузиуса. Энтропия как функция макросостояния. Изменение эн –
тропии в квазистатических процессах. Изменение энтропии в неравновесных
(необратимых ) процессах. Неравенство Клаузиуса. Различные формулировки второго
начала термодинамики. Энтропия идеального газа.
10.4. Тепловые двигатели. Цикл Карно. Теорема Карно. КПД необратимых теп –
ловых двигателей.
1

2.

Макро – и микросостояния макроскопической системы. Статистический вес
макросостояния и вероятность макросостояния. Статистический вес различных
макросостояний (на примере распределения молекул по половинкам сосуда).
Мультипликативность статистического веса.
Макросостояние макроскопической системы (тела)
– задается с помощью объема, давления, температуры, внутренней энергии и др.
макроскопических (характеризующих всю систему в целом) параметров.
Микросостояние макроскопической системы (тела)
– определяется заданием состояний всех молекул тела т.е. всех микрообъектов,
из которых состоит данная макроскопическая система.
Всякое макросостояние может быть реализовано различными способами, каждому
из которых соответствует некоторое микросостояние тела.
Число различных микросостояний, соответствующих данному макросостоянию,
называется статистическим весом или термодинамической вероятностью мак –
росостояния.
2

3.

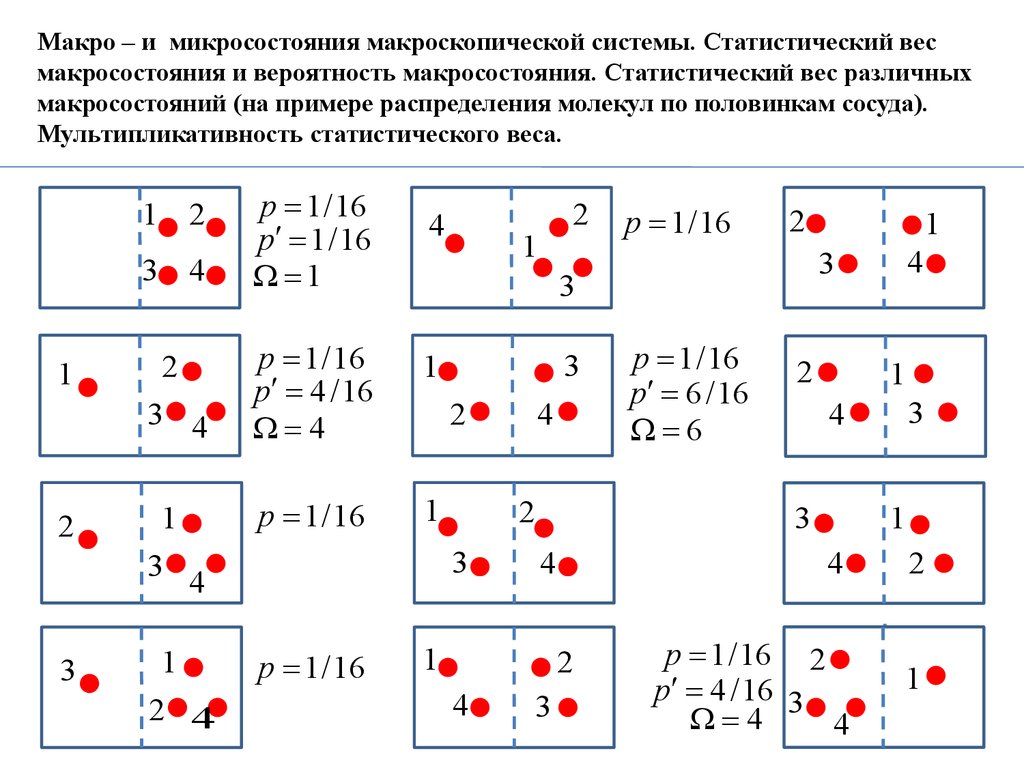
Макро – и микросостояния макроскопической системы. Статистический вес
макросостояния и вероятность макросостояния. Статистический вес различных
макросостояний (на примере распределения молекул по половинкам сосуда).
Мультипликативность статистического веса.
1 2
3 4
1
2
4
1
3 4
1
p 1 / 16
1
2 4
1
3
2
3
p 1 / 16
4
2
4
1
2
p 1 / 16
2
p 1 / 16
p 6 / 16
6
2
4
2
3
4
1
3
4
3
1
4
1
3
3
p 1 / 16
p 4 / 16
4
2
3
3
p 1 / 16
p 1 / 16
1
1
4
2
p 1 / 16 2
p 4 / 16 3
4
4
1
3

4.

Макро – и микросостояния макроскопической системы. Статистический вес
макросостояния и вероятность макросостояния. Статистический вес различных
макросостояний (на примере распределения молекул по половинкам сосуда).
Мультипликативность статистического веса.
Эргодическая гипотеза:
вероятности всех микросостояний одинаковы.
N – полное число всех возможных микросостояний системы,
p – вероятность микросостояния,
– статистический вес макросостояния,
p – вероятность (обычная) макросостояния.
Связь между ними:
Распределение
p
1
,
N
N молекул
p
p ,
N
по половинкам сосуда (
N!
N 2 ; ( n, N n ) C
,
n!( N n)!
N
n
N
p ~
n
,
N n
).
N
n
max , p pmax
2
Система состоит из двух практически не взаимодействующих частей 1 и 2:
1 2
4

5.

Энтропия и ее свойства. Второе начало термодинамики. Третье начало термо –
динамики (теорема Нернста).
Статистический вес мультипликативен:
Аддитивность:
1 2
ln ln 1 ln 2
Энтропия – мера степени молекулярного беспорядка в системе:
S k ln
1) Энтропия изолированной системы при протекании необратимого процесса
возрастает.
2) Энтропия изолированной системы, находящейся в равновесном состоянии,
максимальна.
Закон возрастания энтропии – второе начало термодинамики:
Энтропия изолированной системы может только возрастать:
dS 0
Направление процессов в изолированных макроскопических системах – от состо –
яний с меньшей вероятностью к состояниям с более высокой вероятностью
Теорема Нернста – третье начало термодинамики:
T 0
1,
lim S 0
T 0
5

6.

Равенство Клаузиуса. Энтропия как функция макросостояния. Изменение эн –
тропии в квазистатических процессах. Изменение энтропии в неравновесных
(необратимых ) процессах. Неравенство Клаузиуса. Различные формулировки
второго начала термодинамики. Энтропия идеального газа.
Равенство Клаузиуса:
для любого обратимого цикла
Q
T 0
Q
dS
,
T
V2 ,T2
Q
и для любого обратимого процесса S S 2 S1
.
T
V1 ,T1
S ( V , T ,...) – энтропия.
Q
Q
Необратимые процессы: dS
,
0
T
T
Существует такая функция состояния S ( V ,
Неравенство Клаузиуса (общий случай):
Q
dS
,
T
Q
T 0
T ,...)
, что
Замечание по хронологии:
Нер. Клаузиуса – 1850г.
Теорема Карно – 1824г.
6

7.

Равенство Клаузиуса. Энтропия как функция макросостояния. Изменение эн –
тропии в квазистатических процессах. Изменение энтропии в неравновесных
(необратимых ) процессах. Неравенство Клаузиуса. Различные формулировки
второго начала термодинамики. Энтропия идеального газа.
Различные формулировки второго начала термодинамики.
1) Закон неубывания энтропии (статистическая формулировка):
dS 0
2) Клаузиус: невозможны такие процессы, единственным конечным результатом
которых был бы переход тепла от тела, менее нагретого, к телу, более нагретому.
3) Кельвин: невозможны такие процессы, единственным конечным результатом
которых явилось бы отнятие от некоторого тела определенного количества теп –
ла и превращение этого тепла полностью в работу.
*) невозможен перпетуум мобиле второго рода, т.е. такой периодически действую –
щий двигатель, который получал бы тепло от одного резервуара и превращал это
тепло полностью в работу.
Приведенные формулировки второго начала термодинамики эквивалентны
7

8.

Равенство Клаузиуса. Энтропия как функция макросостояния. Изменение эн –
тропии в квазистатических процессах. Изменение энтропии в неравновесных
(необратимых ) процессах. Неравенство Клаузиуса. Различные формулировки
второго начала термодинамики. Энтропия идеального газа.
Приведенные формулировки второго начала термодинамики эквивалентны
Покажем: для процесса, запрещенного формулировкой Клаузиуса,
C
T10 T20
T10
Q0
C
C
C
T1 T10 T20 T2
T20
T1
T2
Q C T .
Q CdT , C const
T1 T10 Q0 / C , T2 T20 Q0 / C ,
Q CdT
dS
.
T
T
S 0 .
T1
CdT
T1
S1
C ln ,
T
T10
T10
S S1 S 2 C ln
T2 T20 T10 T1
T2
S 2 C ln
,
T20
T1
T
TT
C ln 2 C ln 1 2 .
T10
T20
T10T20
8

9.

Равенство Клаузиуса. Энтропия как функция макросостояния. Изменение эн –
тропии в квазистатических процессах. Изменение энтропии в неравновесных
(необратимых ) процессах. Неравенство Клаузиуса. Различные формулировки
второго начала термодинамики. Энтропия идеального газа.
T1 T2
S C ln
.
T10T20
Обратимость процессов!
T1 T10 Q0 / C , T2 T20 Q0 / C
T1 T10 , T2 T20 ,
Q0 / C 0.
(T20 T10 ) 2
(T20 ) (T10 )
,
S C ln
C ln 1
T10T20
T10T20
T10T20
(T20 T10 ) 2
1
1
T10T20
T10T20
S 0
Такой процесс в замкнутой системе запрещен
законом возрастания энтропии !
9

10.

Равенство Клаузиуса. Энтропия как функция макросостояния. Изменение эн –
тропии в квазистатических процессах. Изменение энтропии в неравновесных
(необратимых ) процессах. Неравенство Клаузиуса. Различные формулировки
второго начала термодинамики. Энтропия идеального газа.
Энтропия идеального газа.
V ,T
S (V , T )
0
Q
,
T
S
V0 ,T0
0
V ,T
Q
Q
,
T V0 ,T0 T
S (V0 , T0 )
V0 ,T0
0
Q
,
T
V ,T
Q
S (V , T ) S (V0 , T0 )
T
V0 ,T0
RT
dV
V
V ,T
T
V
Q
CV dT
R dV
T
T
V
V0 ,T0
T0
V0
Q dU A CV dT pdV . pV RT
Q CV dT R dV
T
T
V
Q CV dT
V ,T
Q
T
V
CV ln R ln
T
T0
V0
V0 ,T0
S (V , T ) S (V0 , T0 ) CV ln
T
V
R ln
T0
V0
10

11.

Равенство Клаузиуса. Энтропия как функция макросостояния. Изменение эн –
тропии в квазистатических процессах. Изменение энтропии в неравновесных
(необратимых ) процессах. Неравенство Клаузиуса. Различные формулировки
второго начала термодинамики. Энтропия идеального газа.
Энтропия идеального газа:
S (V , T ) S (V0 , T0 ) CV ln
T
V
R ln
T0
V0
S (V , T ) CV ln T R ln V S 0
Переход к другим переменным:
pV RT
RT
, ln V ln T ln p ln ( R )
p
S ( p, T ) CV ln T R (ln T ln p ln ( R)) S 0 .
V
S ( p, T ) (CV R) ln T R ln p S 0 ,
C P CV R
S ( p, T ) C P ln T R ln p S 0
S (V , T )
S ( p, V )
– аналогично.
11

12.

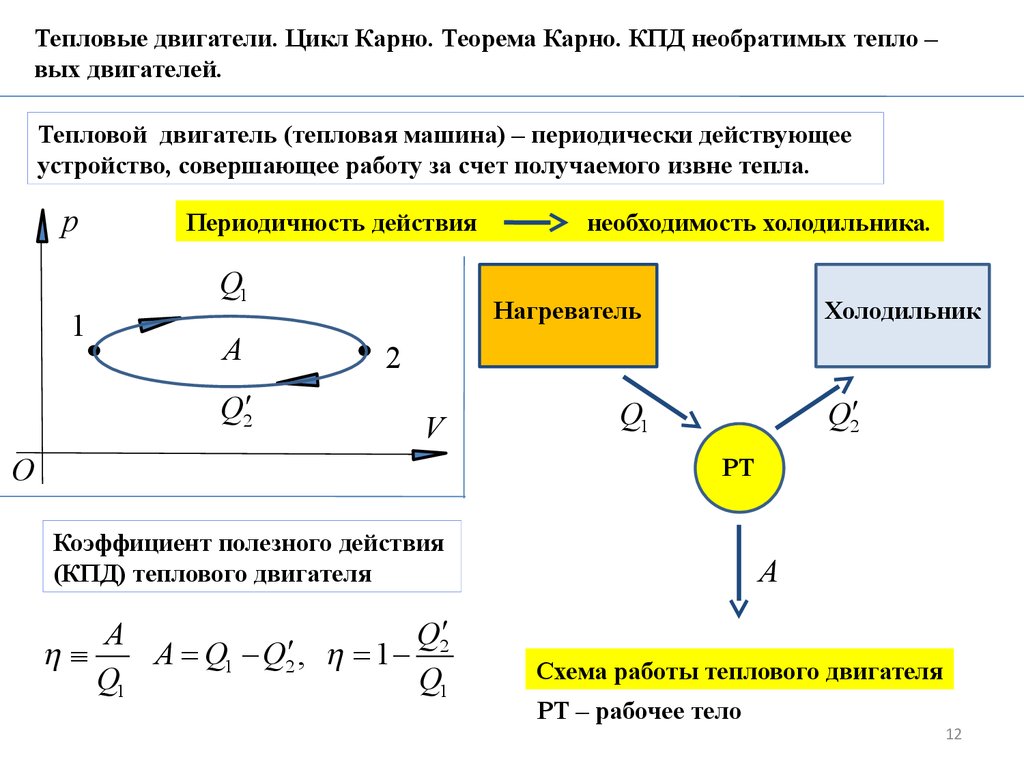
Тепловые двигатели. Цикл Карно. Теорема Карно. КПД необратимых тепло –
вых двигателей.
Тепловой двигатель (тепловая машина) – периодически действующее
устройство, совершающее работу за счет получаемого извне тепла.
p
Периодичность действия
Q1
1
A
Q2
необходимость холодильника.
Нагреватель
Холодильник
2
V
O
Q2
Q1
РТ
Коэффициент полезного действия
(КПД) теплового двигателя
A
Q2
A Q1 Q2 , 1
Q1
Q1
A
Схема работы теплового двигателя
РТ – рабочее тело
12

13.

Тепловые двигатели. Цикл Карно. Теорема Карно. КПД необратимых тепло –
вых двигателей.
Единственный обратимый процесс передачи тепла – изотермический при
температуре термостата (теплового резервуара).
Обратимый цикл – цикл Карно: две изотермы (
( S const ).
Q1
1
2
2
Q1 TdS T1 ( S 2 S1 )
1
\
T2
O
) и две адиабаты
Q TdS ,
T
T1
T const
4
S1
Q1 Q2
T1 T2
4
Q2
3
S2
Q2 T2
.
Q1 T1
S
Q2 TdS T2 ( S1 S 2 ),
3
Q2 Q2 T2 ( S 2 S1 )
Q1 Q2
Q2
T2
1
1
Q1
Q1
T1
13

14.

Тепловые двигатели. Цикл Карно. Теорема Карно. КПД необратимых тепло –
вых двигателей.
T2
1
T1
Теорема Карно:
КПД всех обратимых тепловых двигателей не зависит от рода
рабочего вещества и определяется только температурами на –
гревателя и холодильника: при данных температурах нагрева –
теля и холодильника КПД всех обратимых тепловых двигателей
одинаковы.
«Внесём» необратимость в цикл Карно.
Неравенство Клаузиуса для необратимых процессов:
Q
dS
T
Q Q1
S12
,
T
T1
1
Q Q2
Q2
S 34
,
T
T2
T2
3
4
2
Q
dS
,
T
Q
T 0
Q
S 23
0,
T
2
3
Q
S 41
0,
T
4
1
14

15.

Тепловые двигатели. Цикл Карно. Теорема Карно. КПД необратимых тепло –
вых двигателей.
Q1
Q2
S12 , S 23 0 , S34 , S 41 0
T1
T2
Q1 Q2
Q1 Q2
S12 S 23 S34 S 41
0
T1 T2
T1 T2
Q2 T2
Q1 T1
Q2
T2
1
1 .
Q1
T1
H O
( Теорема Карно):
КПД необратимой тепловой машины всегда меньше, чем КПД обратимой,
работающей в тех же условиях, т.е. при тех же температурах нагревателя и
холодильника.
T2
H 1
T1
Задание: найти более короткое доказательство (теоремы Карно).
15

16.

Тепловые двигатели. Цикл Карно. Теорема Карно. КПД необратимых тепло –
вых двигателей.
p
1
2
4
3
V
O
Цикл Карно для идеального газа (тепловая машина).
1
2
2, 3
3, 4
4 – изотермы;
1 – адиабаты.
16

17.

Тепловые двигатели. Цикл Карно. Теорема Карно. КПД необратимых тепло –
вых двигателей.
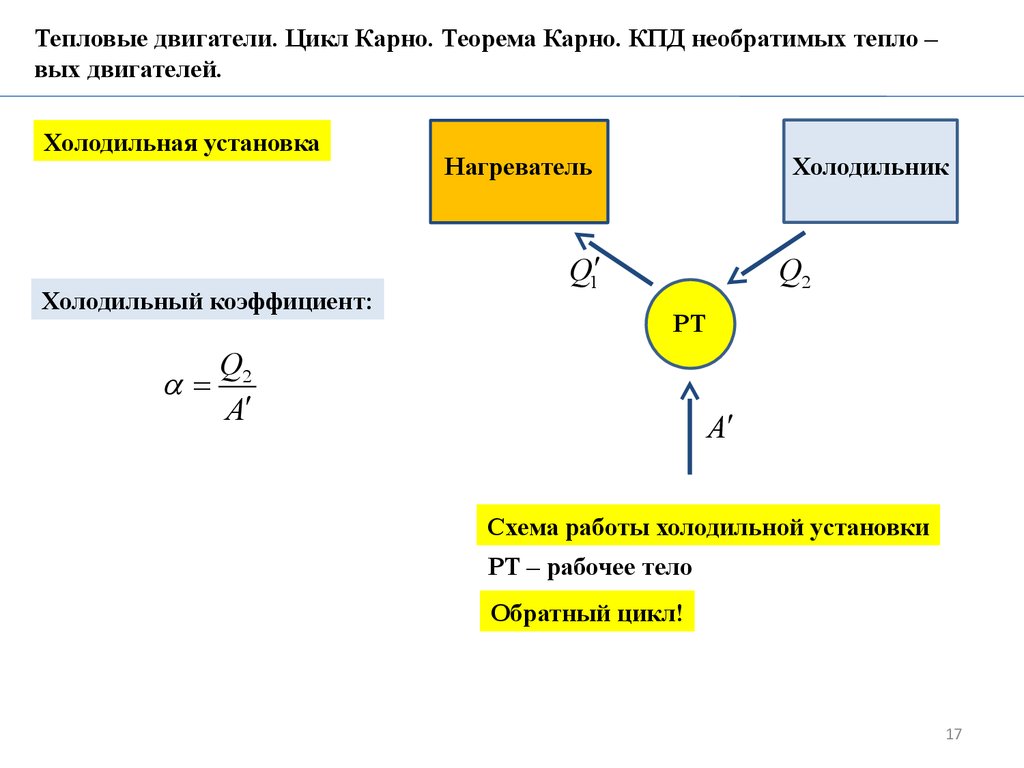
Холодильная установка
Холодильный коэффициент:
Холодильник
Нагреватель
Q1
Q2
РТ
Q2
A
A
Схема работы холодильной установки
РТ – рабочее тело
Обратный цикл!
17