Анализ сложности и эффективности алгоритмов. (Лекция 4)

1. Лекция № 4

Тема: Анализ сложности и
эффективности алгоритмов
1

2.

• Под трудоёмкостью алгоритма для данного
конкретного входа – (N), будем понимать
количество
«элементарных»
операций
совершаемых
алгоритмом
для
решения
конкретной проблемы в данной формальной
системе.
• Оценка
функции
трудоемкости
алгоритма
называется сложностью алгоритма и позволяет
определить предпочтения в использовании того
или иного алгоритма для больших значений
размерности исходных данных.
2

3. Основные понятия

• В самом широком смысле понятие
эффективности связано со всеми
вычислительными ресурсами,
необходимыми для работы алгоритма.
• В узком смысле под "самым
эффективным" алгоритмом понимается
самый быстрый.
• Ограничения по времени является
доминирующим фактором,
определяющим пригодность
конкретного алгоритма для практики.
3

4. Критерии эффективности алгоритма:

• Временная эффективность (или
временная сложность) программы по
соответствующему алгоритму,
определяется временем, необходимым
для ее выполнения.
• Пространственная характеристика
(емкость) измеряется количеством
памяти, требуемой для выполнения
программы соответствующего
алгоритма.
4

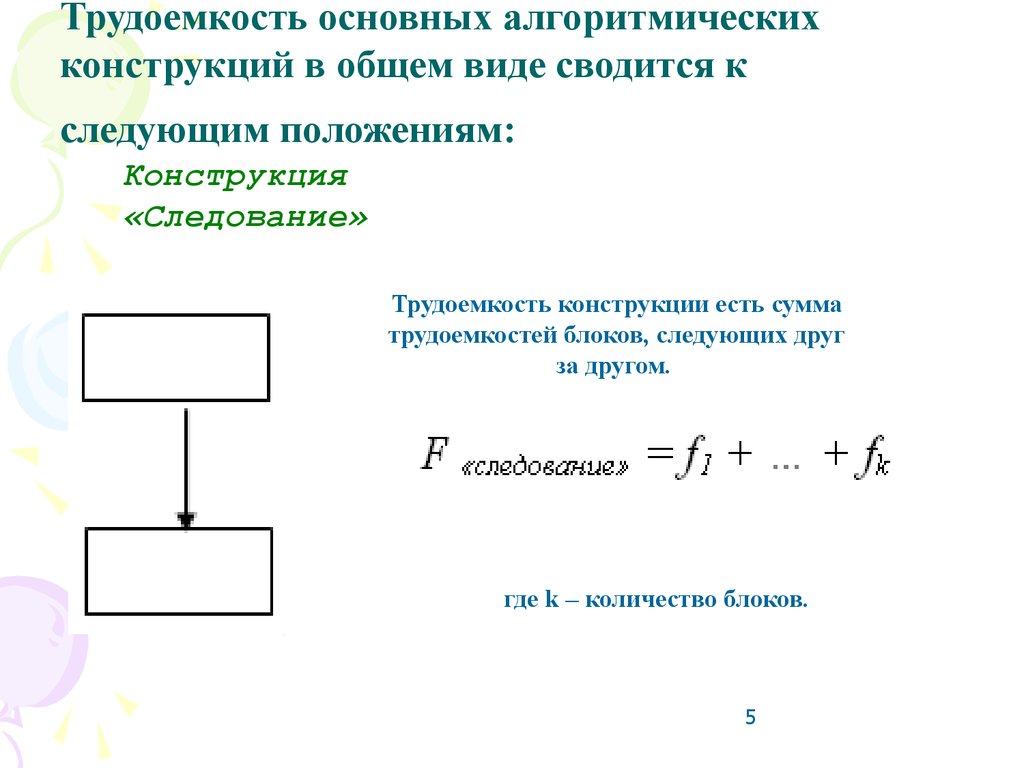
5. Трудоемкость основных алгоритмических конструкций в общем виде сводится к следующим положениям:

Конструкция
«Следование»
Трудоемкость конструкции есть сумма
трудоемкостей блоков, следующих друг
за другом.
где k – количество блоков.
5

6.

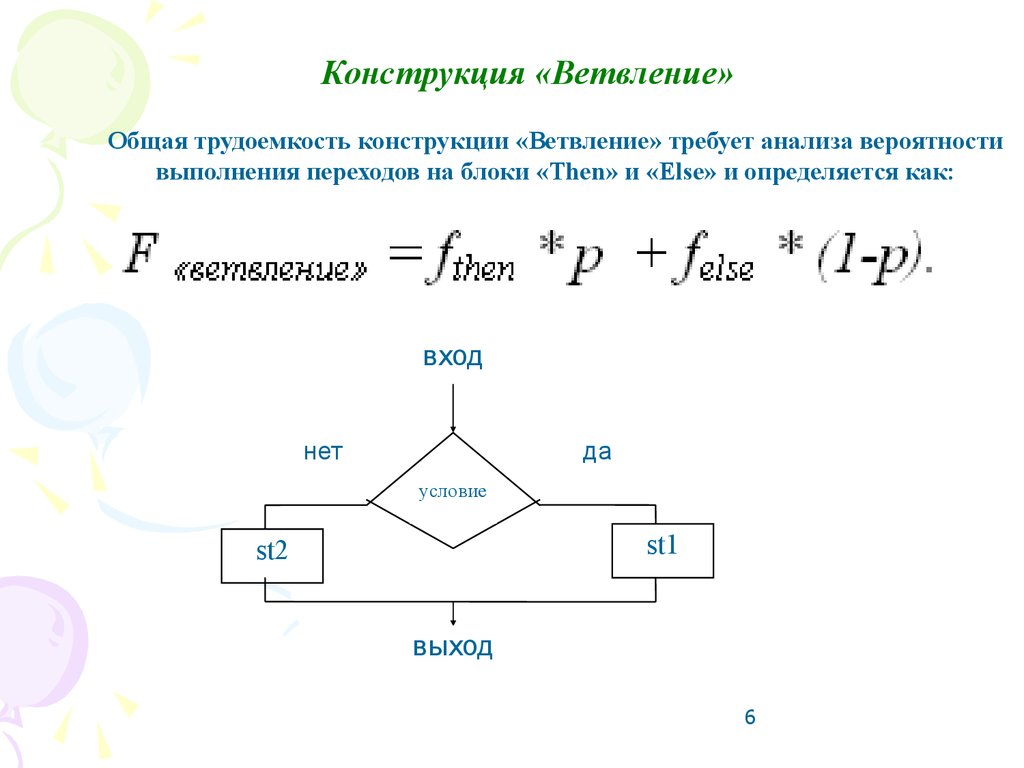
Конструкция «Ветвление»
Общая трудоемкость конструкции «Ветвление» требует анализа вероятности
выполнения переходов на блоки «Then» и «Else» и определяется как:
вход
да
нет
условие
st1
st2
выход
6

7.

Конструкция «Цикл»
После сведения конструкции к элементарным операциям
ее трудоемкость определяется как:
7

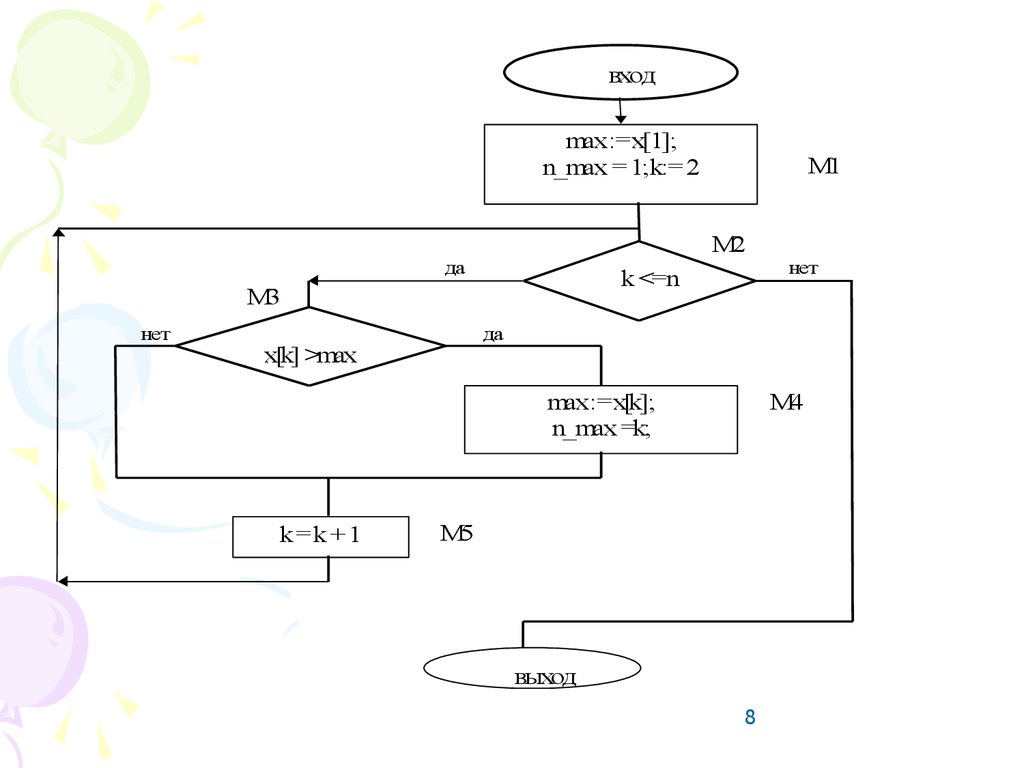
8.

вход
max:=x[1];
n_max = 1;k:= 2
M2
да
k <=n
M3
нет
M1
да
x[k] >mах
max:=x[k];
n_max =k;
k =k + 1
нет
M4
M5
выход
8

9.

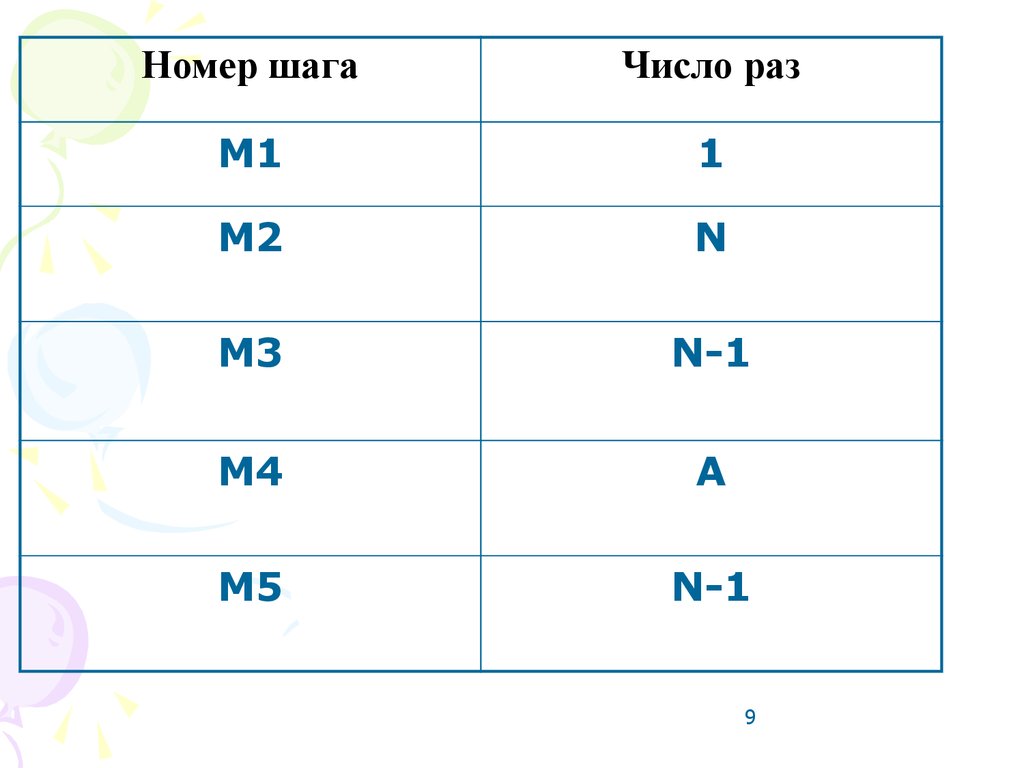
Номер шага
Число раз
М1
1
М2
N
М3
N-1
М4
A
М5
N-1
9

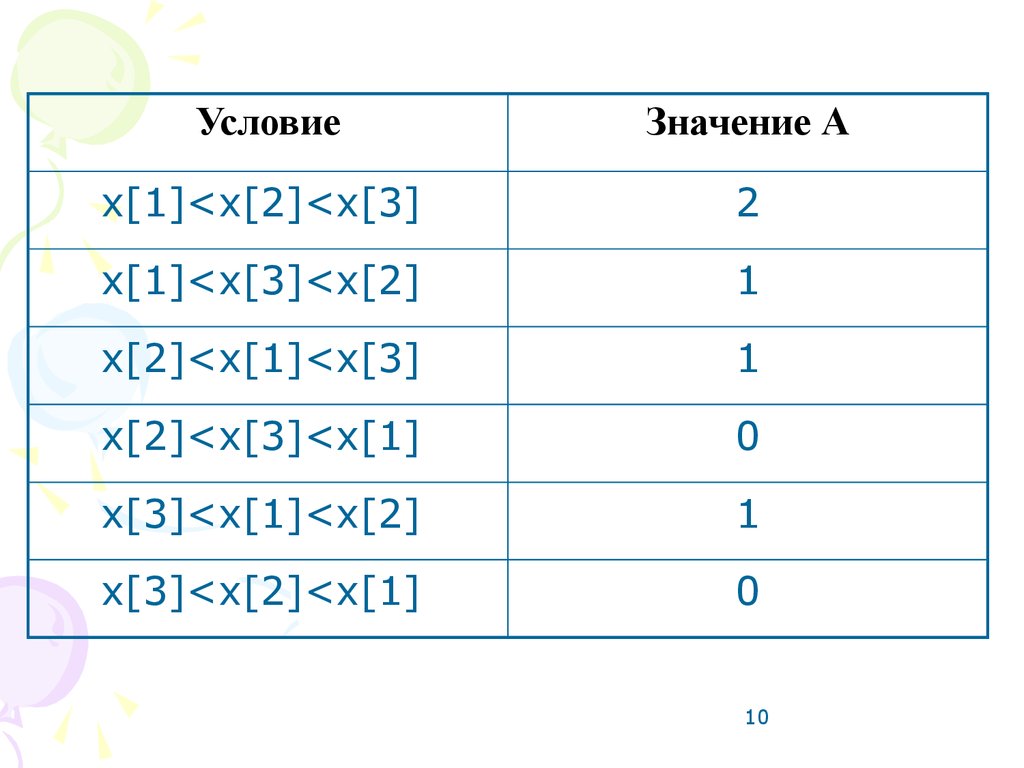
10.

Условие
Значение А
x[1]<x[2]<x[3]
2
x[1]<x[3]<x[2]
1
x[2]<x[1]<x[3]
1
x[2]<x[3]<x[1]
0
x[3]<x[1]<x[2]
1
x[3]<x[2]<x[1]
0
10

11.

Amin=0, при mах=x[1]
Amax=n-1, при x[1]<x[2]< ...<x[n]
Aср=(0+1+0+1+1+2)/6=5/6
11

12.

Временная сложность алгоритма:
Vmin=М1+М2+М3+М4+М5=1+N+
(N-1)+0+(N-1)=3N-1
Vmax=М1+М2+М3+М4+М5=1+N
+(N-1)+(N-1)+(N-1)=4N-2
Vср=М1+М2+М3+М4+М5=1+N+
(N-1)+5/6+(N-1)=3N-0,16
12

13. Два класса алгоритмов:

• Экспоненциальные алгоритмы алгоритмы "неэффективные"
просто варианты полного перебора
• Полиномиальные алгоритмы –
алгоритмы "эффективные", или
"хорошие" алгоритмы, когда
удается более глубоко проникнуть
в суть решаемой задачи
13

14.

Время работы алгоритма удобно
выражать в виде функции от одной
переменной, характеризующей
“размер” индивидуальной задачи,
т.е. объем входных данных,
требуемых для описания задачи
• Экспоненциальный алгоритм
называется алгоритм, у которого
временная сложность равна Pn
• Полиномиальным алгоритмом
называется алгоритм, у которого
временная сложность равна np
14

15. Сравнение нескольких полиномиальных и экспоненциальных функций временной сложности

Функция
временной
сложности
Размер п
10
20
30
40
50
60
n
0,00001 сек
0,00002 сек
0,00003 сек
0,00004 сек
0,00005 сек
0,00006 сек
n2
0,0001 сек
0,0004 сек
0,0009 сек
0,0016 сек
0,0025 сек
0,0036 сек
n3
0,001 сек
0,008 сек
0,027 сек
0,064 cек
0,125 сек
0,216 сек
n5
0,1 сек
3,2 сек
24,3 сек
1,7 мин
5,2 мин
13,0 мин
2n
0,001 сек
1,0 сек
17,9 мин
12,7 дней
35,7 лет
366 столетий
3n
0,059 сек
58 мин
6,5 лет
3855 столетий
2х108 столетий
1,3х1013
столетий
15