Математическое моделирование авиационных двигателей

1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ АВИАЦИОННЫХ ДВИГАТЕЛЕЙ

ПНИПУ
Кафедра: Авиационные двигатели.
Курс лекций.
Автор: доктор технических наук, профессор
Августинович Валерий Георгиевич
2018

2.

УРОВНИ ГОТОВНОСТИ И РИСКА ПРОЕКТА
№
п/
п
9
8
7
6
5
4
3
2
1
0
Уровень готовности
В реальной системе в
эксплуатации
Сертифицирована
Демонстрация в прототипе
системы в полете
Демонстрация в системе в
рабочих условиях
В узле в рабочих условиях (стенд.
ГГ)
В узле в лабораторных условиях
Экспериментально
подтверждена концепция
Сформулирована концепция
технологии
Базовые принципы проверены на
математических моделях и
опубликованы
Не сформулирована концепция—
базовые принципы
Уровень риска
%%
10
20
30
40
50
60
70
80
90
100

3. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КАМЕРЫ СГОРАНИЯ: (закон Гесса)

Закон Гесса. Связь между количеством топлива и параметрами в начале и в
конце процесса подвода тепла в камере сгорания устанавливается в
соответствии с законом Гесса:
Тепловой эффект реакции является функцией состояния системы, т.е.
зависит только от ее начального и конечного состояний и не зависит от
промежуточных стадий (т.е. пути перехода от начального к конечному
состоянию).
первый закон термодинамики
dQ du pdυ
может быть выражен в виде dQ du pdυ υdp (т.к. dp = 0) и,
учитывая, что di du d pυ , получим dQ = di (т.е. закон Гесса, т.к.
энтальпия есть функция состояния системы).

4. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КАМЕРЫ СГОРАНИЯ: (уравнение баланса энергии на фронте пламени)

Уравнение баланса энергии для этого процесса имеет вид
QpÒBC
T2*
c T dT QpÏ Ñ
25 p
T3*
c T dT .
25 p

5. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КАМЕРЫ СГОРАНИЯ: (теоретически необходимое кол-во окислителя для полного окисления горючего)

Валентности основных химических элементов
для возможных видов горючего и окислителя
H
He
Li
Be
B
C
N
O
F
Ne
Na
Mg
Al
S
–1
0
–1
–2
–3
–4
0
+2
+1
0
–1
–2
–3
+2
Общая формула для определения L0 для любого сочетания
горючего и окислителя ( полное замещение валентностей )
L0
i
,
i
ãî ð
î êèñë
где i – количество грамм-атомов, – валентность

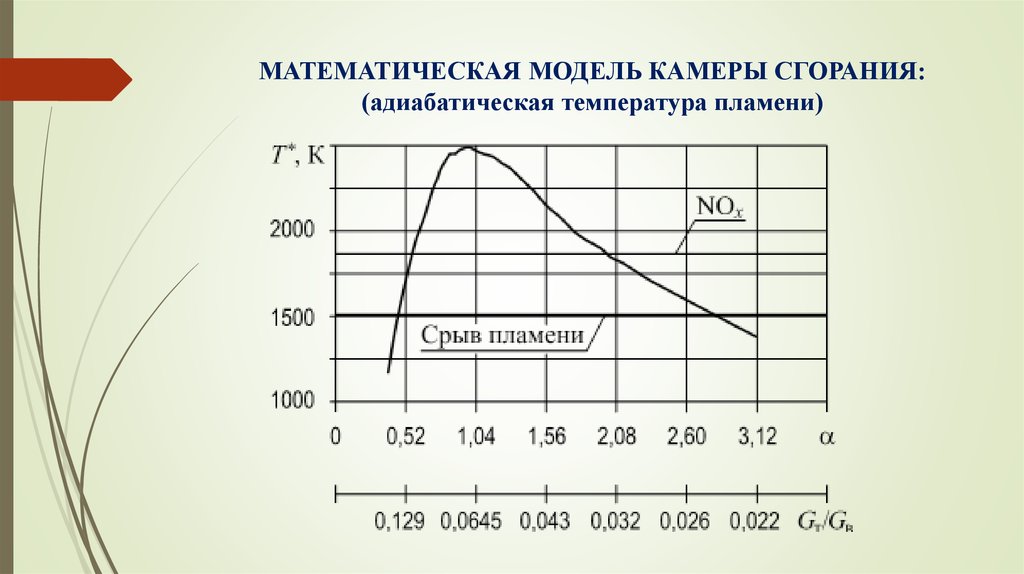
6. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КАМЕРЫ СГОРАНИЯ: (условия устойчивого горения)

Условия
устойчивого
г о р е н и я . Пламя может
распространяться только в смесях, состав которых находится в
определенных
концентрационных
пределах.
Параметром,
характеризующим концентрационный состав смеси, является
G
коэффициент избытка воздуха â , где L0 – теоретически
Gò L0
необходимое количество воздуха для полного окисления 1 кг топлива.
Смесь, имеющая =1, называется стехиометрической,
1 – бедной, а <1 – богатой. Соответственно,
состав продуктов сгорания и тепловой эффект
реакции, равный разности теплот образования
продуктов сгорания и исходного химического
вещества, зависит от параметра . Следовательно, и
температура пламени (продуктов сгорания) является
функцией

7. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КАМЕРЫ СГОРАНИЯ: (адиабатическая температура пламени)

8. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КАМЕРЫ СГОРАНИЯ: (подготовка топливо-воздушной смеси)

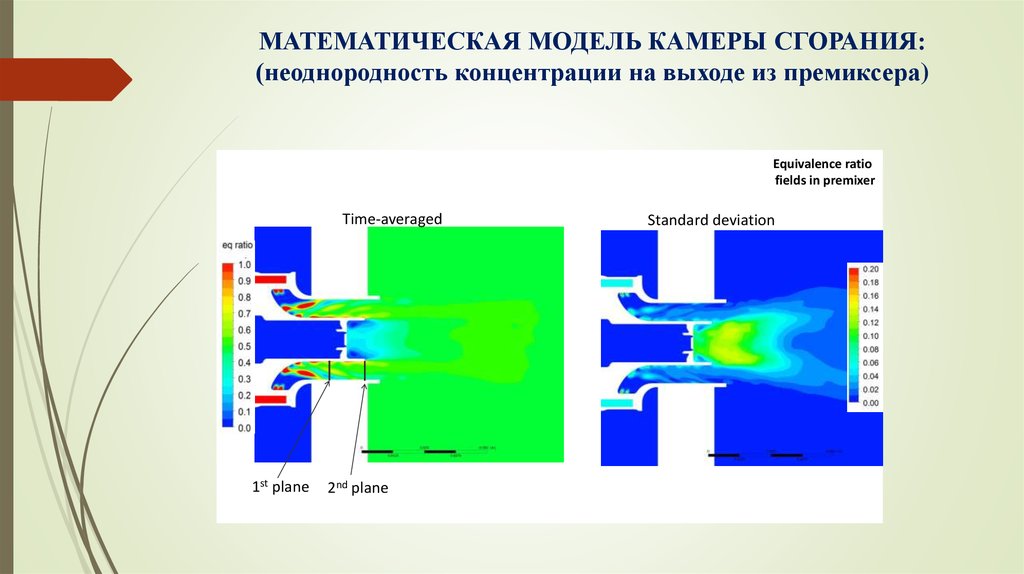
9. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КАМЕРЫ СГОРАНИЯ: (неоднородность концентрации на выходе из премиксера)

Equivalence ratio
fields in premixer
Time-averaged
1st plane
2nd plane
Standard deviation

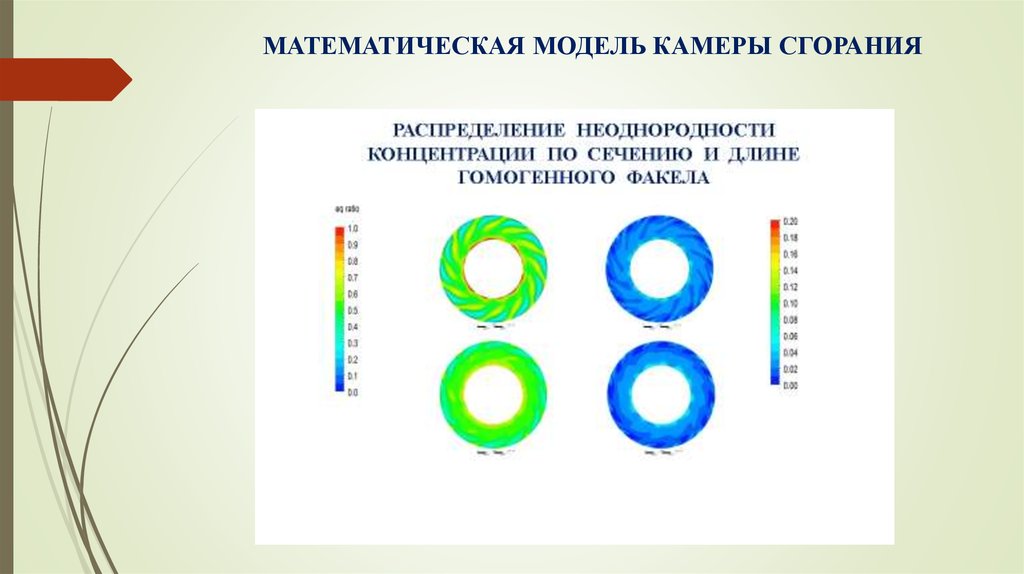
10. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КАМЕРЫ СГОРАНИЯ

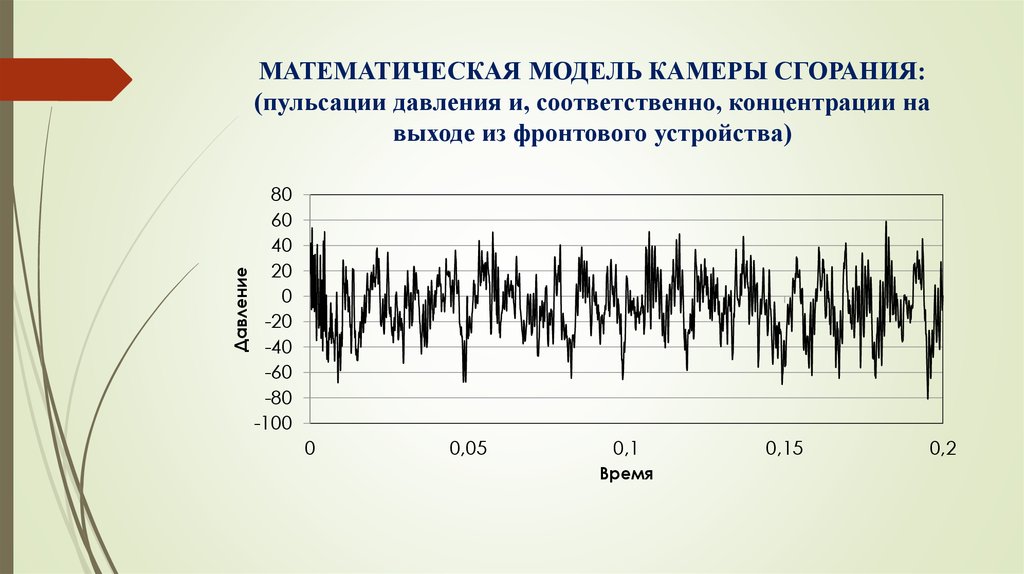
11. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КАМЕРЫ СГОРАНИЯ: (пульсации давления и, соответственно, концентрации на выходе из фронтового устройства)

Давление
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КАМЕРЫ СГОРАНИЯ:
(пульсации давления и, соответственно, концентрации на
выходе из фронтового устройства)
80
60
40
20
0
-20
-40
-60
-80
-100
0
0,05
0,1
Время
0,15
0,2

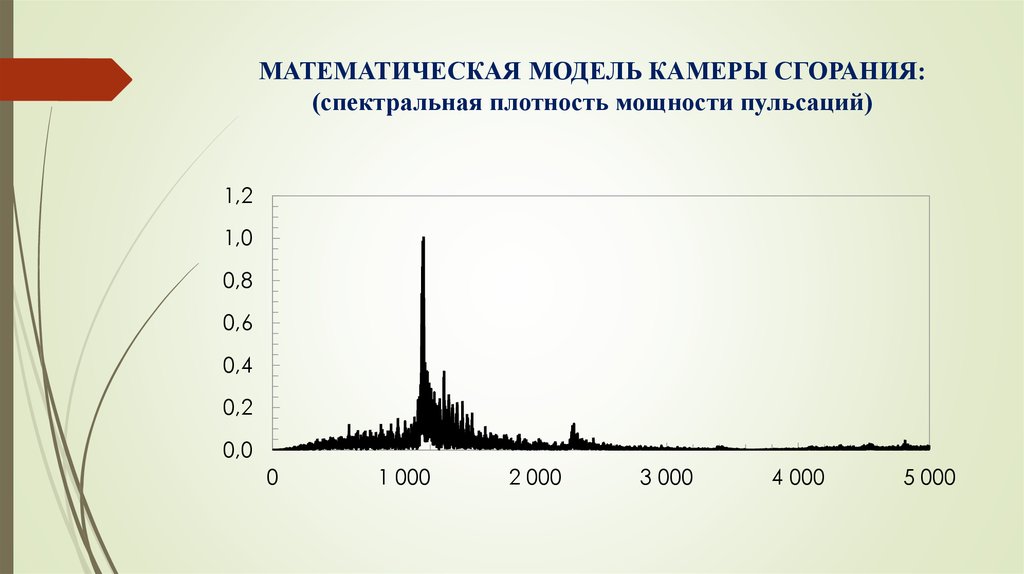
12. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КАМЕРЫ СГОРАНИЯ: (спектральная плотность мощности пульсаций)

1,2
1,0
0,8
0,6
0,4
0,2
0,0
0
1 000
2 000
3 000
4 000
5 000

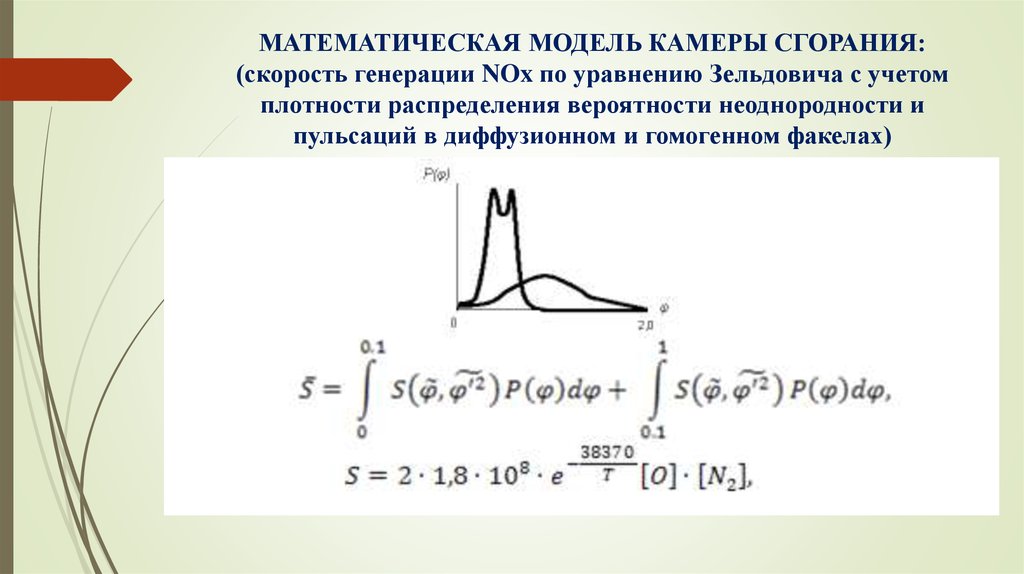
13. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КАМЕРЫ СГОРАНИЯ: (скорость генерации NOx по уравнению Зельдовича с учетом плотности распределения

вероятности неоднородности и
пульсаций в диффузионном и гомогенном факелах)

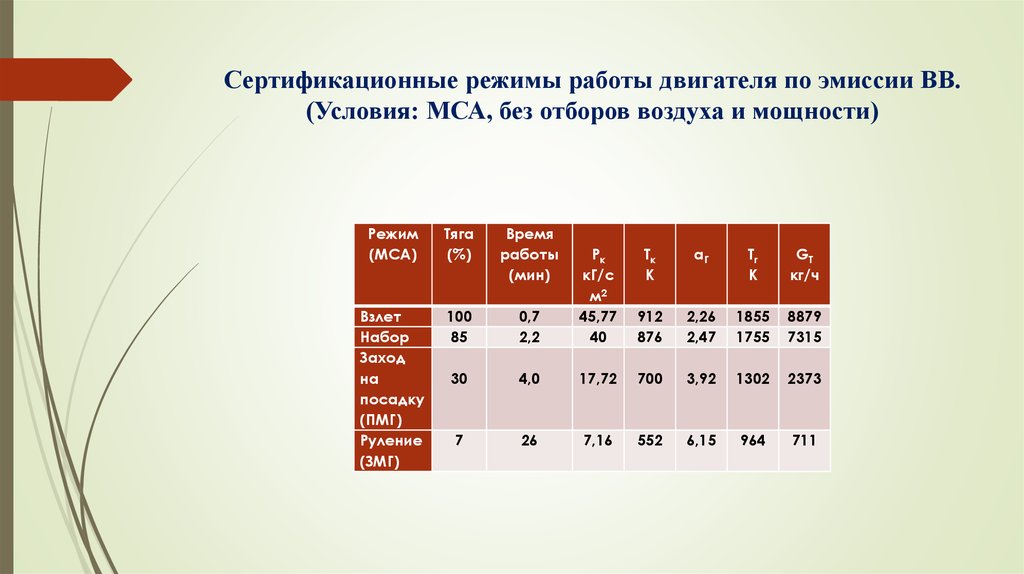
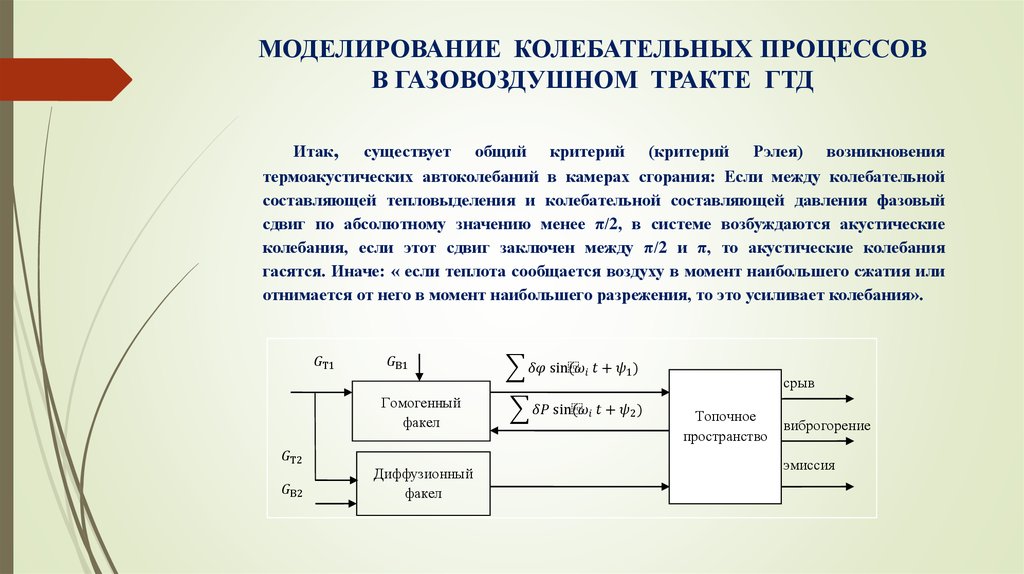
14. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КАМЕРЫ СГОРАНИЯ:

Далее необходимо произвести осреднение скорости генерации окислов азота
по длине топочного пространства (L) камеры сгорания, для чего принимается
экспоненциальная зависимость, представленная ниже: