Similar presentations:
Теория радиоактивных методов
1. ТЕОРИЯ РАДИОАКТИВНЫХ МЕТОДОВ
1. Гамма-каротажинтегральный (ГК)
2. Гамма-каротаж
спектрометрический (ГК-С)
1
2. Радиоактивность осадочных горных пород. Радионуклиды.
Гамма-излучение калия (40К)монохроматично - 1,46 МэВ.
Энергетические спектры
элементов урановых (238U,
235U) и ториевого (232Th)
рядов имеют несколько
линий, наиболее
интенсивные— 242, 355, 609,
1120, 1765 кэВ и 238, 338,
583, 911, 969, 1587, 2620 кэВ
соответственно.
2
3.
Радиоактивность горных породАктивность а одного кубического метра вещества
называют удельной объемной активностью.
Величину am=a/d (δ — плотность вещества)
называют удельной массовой активностью.
Для практических целей используют удельную
объемную концентрацию Qj, определяющую
содержание j-го естественного радиоактивного
элемента (ЕРЭ) в граммах в 1 сантиметре
кубическом,
и относительную величину — удельную
массовую концентрацию
qj = Qj / δ.
18.01.2019
3
4.
Решение прямой задачи интегрального ГКРешение прямой задачи заключается в
нахождении зависимости показаний
прибора от содержания ЕРЭ в пласте,
вмещающих породах и промежуточных
зонах — скважине, цементе, колонне.
При приближенном аналитическом
решении многократное рассеяние
квантов учитывают, вводя фактор
накопления В.
Поток излучения в любой точке считают
созданным отдельными элементарными
объемами, детектор точечным, а
источники равномерно распределенными
в областях кусочно-однородной среды.
18.01.2019
4
5.
Решение прямой задачи интегрального ГКПлотность потока излучения кусочно-однородного
пространства
1
Фj
4
dV
i a j B j exp i ij li r r 2 .
V
1
где аj — удельная объемная активность j-го ЕРЭ;
Bj – фактор накопления j-го ЕРЭ;
ij — коэффициент ослабления излучения j-го ЕРЭ в i-й среде,
расположенной между точками r и r1;
Δli — длина части отрезка, соединяющего точки r и r1 в среде i.
18.01.2019
5
6.
Решение прямой задачи интегрального ГКПлотность потока излучения для однородной среды
с точечным детектором в начале координат
j r
Bja j e
Bja j
2
Фj
4
r
dr
.
2
4 0 r
j
18.01.2019
6
7.
Решение прямой задачи интегрального ГКB j a j e j r
Bja j
2
Фj
4 r dr
.
2
4 0 r
j
qj = Qj / δ
Так как
a j pj N j / dV . N j / dV N AQ j / A j ..
Получаем
Ф j B j pj N Aq j / Aj mj ,
где: λpj – параметр распада (вероятность распада за единицу
времени) j-го ЕРЭ; Nj /dV - число ядер j-го ЕРЭ в единице
объема; NA - число Авогадро; Aj - атомная масса j-го ЕРЭ;
Qj - объемная концентрация j-го ЕРЭ ; mj = j /d - массовый
коэффициент ослабления излучения j-го ЕРЭ.
7
8.
Решение прямой задачи интегрального ГКПоказания скважинного прибора в однородной
среде, содержащей j-й ЕРЭ,
I j c jФ j c j B j pj N Aq j / Aj mj ,
где сj – аппаратурная постоянная.
Введя коэффициент концентрационной чувствительности (Сj),
характеризующий отклик прибора на излучение единицы
удельной массовой концентрации j-го ЕРЭ,
C j c j B j pj N A / A j mj ,
получим выражение в более компактной форме:
I j = Cj q j .
8
9.
Решение прямой задачи интегрального ГК. Урановыйэквивалент.
Показания скважинного прибора в
однородной
среде, содержащей j-й ЕРЭ,
Ij = CU qj eUj .
где CU – коэффициент концентрационной чувствительности по
урану.
qj – удельные массовые концентрации урана (U), тория (Th) и
калия (K).
eUj – урановые эквиваленты единичной концентрации урана (U),
тория (Th) и калия (K).
Суммарное показание гамма-каротажа
Iγ= CU ∑qj eUj
9
10.
Суммарная удельная массовая концентрациярадионуклидов
Суммарная удельная массовая концентрация смеси
радионуклидов в единицах уранового эквивалента
∑qj eUj = Iγ / CU,
где - Iγ = ∑ Ij скорость счета, зарегистрированная с
помощью интегральной аппаратуры гамма-каротажа.
Коэффициент СU, позволяющий перейти от импульсов в
единицу времени к суммарной концентрации радионуклидов в
1 грамме породы, определяют экспериментально с помощью
образцового источника -излучения.
10
11.
Решение прямой задачи интегрального ГКДля кусочно-однородной
среды, содержащей пласт бесконечной
мощности, плотность потока излучения
равна сумме плотностей потоков,
обусловленных пластом, скважиной,
колонной и цементом
Ф = Фпл + Фс + Фк + Фц.
В сферической системе координат
Δlc = Rc / cosθ;
Δlк = Δк / cosθ;
Δlц = Δц / cosθ;
Δlпл = r - ( Rc+Δк+Δц ) / cosθ
18.01.2019
11
12.
Решение прямой задачи интегрального ГКФ = Фпл + Фс + Фк + Фц
Поток излучения пласта Фплj, содержащего j-и
ЕРЭ
Фплj
Bплjaплj
плj
Где
G ( )
Bплj плj N A qплj
A j плj
/2
G ( )
sin
exp(
/
cos
)
d
0
Δ = Δц цj + Δк кj + Rc cj
18.01.2019
G ( ),
B j a j e j r
Bja j
2
Фj
4 r dr
.
2
4 0 r
j
12
13.
Решение прямой задачи ГК. Геометрический фактор.Плотность Фплj пропорциональна коэффициенту G(Δ), который
зависит от геометрии системы, коэффициентов цj , кj , cj и
характеризует вклад данной области в регистрируемый сигнал.
По существу G(Δ) – аналог геометрического фактора. Для
кусочно-однородной среды, содержащей К областей с j-м ЕРЭ
K
G
1
ij
i 1
18.01.2019
13
14.
Решение прямой задачи ГК. Геометрический фактор.Введя геометрические факторы колонны Gjk , цемента Gjц ,
скважины Gjс , пласта Gjпл=G(Δ), и переходя к показаниям
прибора, для среды, содержащей смесь ЕРЭ, запишем:
I CU qiппeU j G jпп q jceU j G jc q jк eU j G jк q jц eU j G jц .
j
j
j
j
Геометрические факторы областей мало зависят от типа ЕРЭ.
Поэтому уравнение при однородной промежуточной зоне
I GплСU q jппeU j 1 Gпл СU q jппeU j ,
j
q
j
j
суммарная
массовая
удельная
концентрация
ЕРЭ
в
eU
jnn
j
скважине, цементе и колонне.
Iγ= CU ∑qj eUj
18.01.2019
14
15.
Решение прямой задачи ГК. Пласт конечной мощностиПласт конечной мощности, пересеченный необсаженной
скважиной, вызывает приращение плотности потока
ΔФ = Фпл - Фвм,
где Фвм — плотность потока излучения во вмещающих породах.
Если параметры В, ж и G против пласта и вмещающих пород
практически равны, то ΔФ равно плотности потока при массовой
активности Δа = апл - авм, где авм — удельная объемная активность
вмещающих пород.
Подставив в вышеприведенные формулы Δа, получим выражение
для ΔФпл, позволяющее рассчитать диаграммы ГК против пласта с
заданными параметрами, для случая для υτя=0.
18.01.2019
15
16.
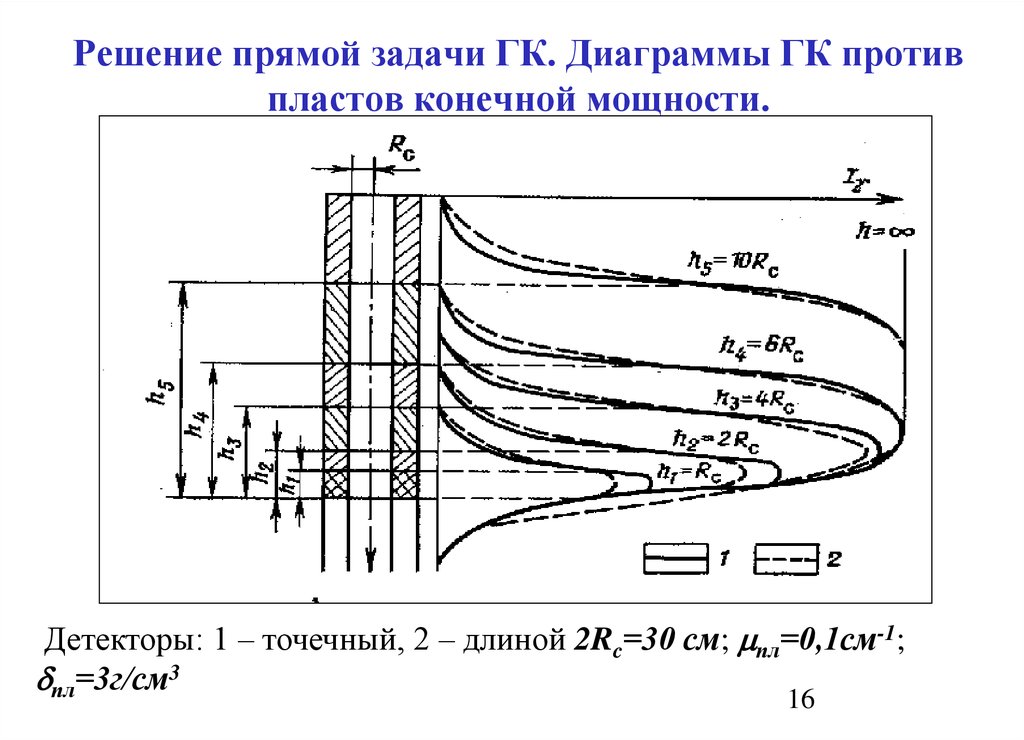
Решение прямой задачи ГК. Диаграммы ГК противпластов конечной мощности.
Детекторы: 1 – точечный, 2 – длиной 2Rc=30 см; пл=0,1см-1;
dпл=3г/см3
16
17.
Спектрометрический гамма-каротаж. СГКПервичный спектр естественного гамма-излучения
пород дает представления о распределении его
интенсивности по энергиям. Этот спектр содержит
характерные максимумы, соответствующие энергиям
определенных ЕРЭ.
Аппаратурный спектр гамма-излучения породы
отмечает
максимумы
первичного
спектра,
соответствующие энергиям 0,6 и 1,8 МэВ для радия
(урана); 0,9; 1,6 и 2,6 МэВ для тория; 1,46 МэВ для
калия.
Дифференциальный
спектр
характеризует
интенсивность I естественного гамма-излучения в
заданном диапазоне энергии Е, причем каждый
18.01.2019
17
диапазон исследуется отдельным каналом.
18.
Спектрометрический гамма-каротаж. СГКДля определения удельных массовых концентраций qu, qTh, qK
по интенсивностям I 1, I 2, I 3, зарегистрированным первым,
вторым и третьим каналами, решают систему уравнений:
I 1 au1qu aTh1qTh ak1qK ;
I 2 aU 2 qU aTh 2 qTh aK 2 qK ;
I 3 aU 3qU aTh 3qTh aK 3qK .
aU , aTh , aK в уравнениях, для конкретного
Коэффициенты
радиометра, определяют путем эталонирования прибора.
18.01.2019
18
19.
Спектрометрический гамма-каротаж. ЗадачиС помощью СГК решают задачи:
1. Детальное литологическое расчленение разрезов,
представленных терригенными, карбонатными, вулканогеннообломочными, магматическими породами.
2. Выделение в плотных карбонатных породах зон
трещиноватости по интервалам повышенного содержания урана
при низком содержании тория и калия. И показаниям других
методов ГИС на отсутствие глинистого материала.
3. Определение минерального состава глинистых пород по
отношению Th/K.
4. Оценка ресурсов органогенного углерода в битуминозных
глинистых нефтематеринских толщах.
5. Контроль перемещения ВНК, разделение продуктивного
коллектора на участки заводненные и не охваченные разработкой.
18.01.2019
19


















 industry
industry








