Исследование операций в логистике

1.

2.

• Матвейчук Наталья Михайловна,
к.ф.-м.н., доцент кафедры ЭИ,
• ауд. 804-5(кафедра), 801а-5
• (44)700-91-83, (29)740-11-63
• [email protected]

3. ТЕМЫ:

1. Задачи нелинейного и целочисленного
линейного программирования
2. Модели управления запасами
3. Динамическое программирование
4. Оптимизационные задачи на графах
5. Марковские процессы
6. Системы массового обслуживания
7. Теория игр
8. Многокритериальная оптимизация
3

4.

Теория игр
Джон Нэш – 1994 (экономика)
Элвин Рот и Ллойд Шепли – 2012 (экономика)
Теория графов
Эдсгер Дейкстра – медаль Филдса – 1972
Ричард М. Карп – медаль Филдса – 1985
СМО
Агнер К. Эрланг (1878-1929) его именем названа единица
интенсивности нагрузки в телекоммуникационных системах
(эрланг)
• Динамическое программирование
• Ричард Беллман - Премии Норберта Винера по прикладной
математике (1970), Диксона (1970), фон Неймана (1976),
Медаль почёта IEEE (1979)
4

5.

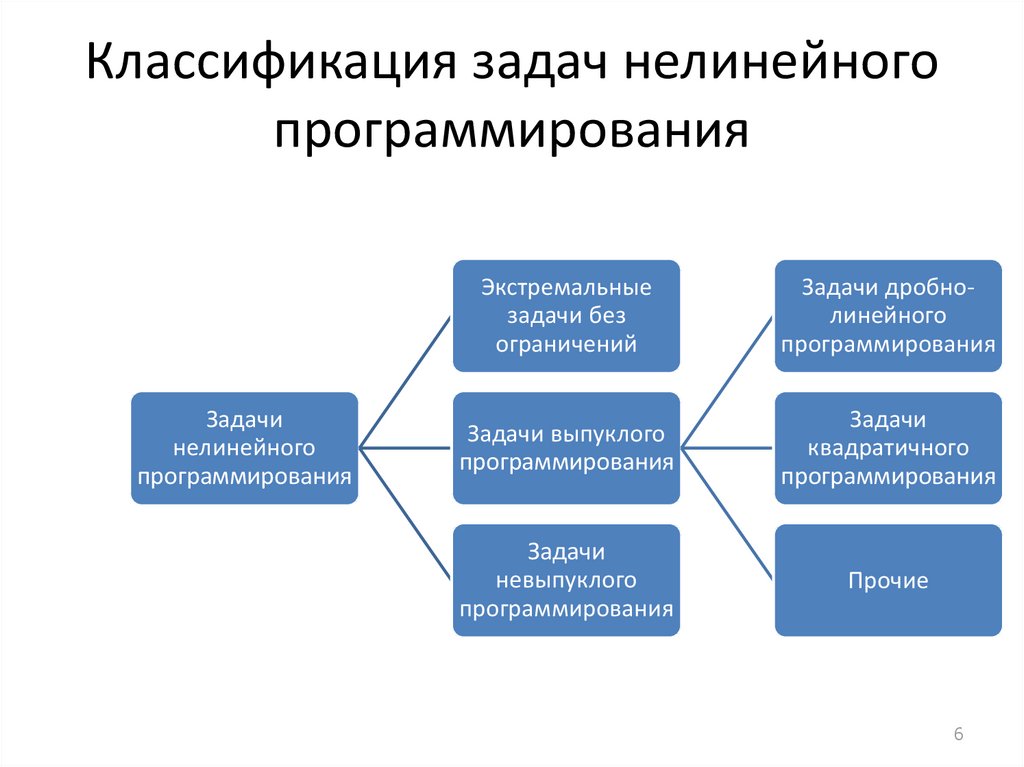
6. Классификация задач нелинейного программирования

Задачи
нелинейного
программирования
Экстремальные
задачи без
ограничений
Задачи дробнолинейного
программирования
Задачи выпуклого
программирования
Задачи
квадратичного
программирования
Задачи
невыпуклого
программирования
Прочие
6

7. Экстремальная задача без ограничений: случай одной переменной

П о в т о р е н и е
Экстремальная задача без ограничений:
случай одной переменной
Постановка задачи: y = f(x) max (min)
Необходимое условие экстремума в точке x0: f’(x0) = 0 (x0 –
стационарная точка)
Достаточные условия экстремума в точке x0 (функция f(x)
должна быть непрерывна вместе со своими
производными первого и второго порядка в этой точке):
- если f”(x0) > 0, то x0 – точка локального минимума,
- если f”(x0) < 0, то x0 – точка локального максимума,
- если f”(x0) = 0, то в точке x0 экстремума нет.
7

8. Экстремальная задача без ограничений: случай двух переменных

П о в т о р е н и е
Экстремальная задача без ограничений:
случай двух переменных
Постановка задачи:
z = f(x, y) max (min)
Необходимое условие экстремума в точке (x0, y0):
((x0 , y0) – стационарная точка)
df ( x 0, y 0)
0
dx
df ( x 0, y 0)
0
dy
Функция f(x, y) должна быть непрерывна
вместе со своими частными производными
первого и второго порядка в этой точке
8

9. Экстремальная задача без ограничений: случай двух переменных

П о в т о р е н и е
Экстремальная задача без ограничений:
случай двух переменных
Достаточные условия экстремума в точке (x0, y0):
обозначим частные производные второго порядка
2 f ( x 0, y 0 )
A
2
x
2 f ( x 0, y 0 )
B
x y
2 f ( x 0, y 0 )
C
2
y
Вычислим D = АС – В2:
• если D > 0, то в точке (x0, y0) функция f(х, у) имеет
локальный максимум при А<0 и локальный минимум при А>0;
• если D < 0, то в точке (x0, y0) функция f(х, у) экстремума
не имеет;
• если D = 0, то требуются дополнительные исследования.
9

10. Экстремальная задача без ограничений: общий случай

Постановка задачи:
y f X f ( x1, x2 , ..., xn ) max(min)
Необходимое условие экстремума в точке
X 0 x10 , x20 , ..., xn0
(Х0 – стационарная точка):
f
f
0
0
f X
X , ...
X 0
xn
x1
0
Функция f(x1,…,xn) непрерывна и имеет в
точке Х0 частные производные, по крайней
мере, второго порядка
10

11. Экстремальная задача без ограничений: общий случай

Достаточные условия экстремума в точке Х0:
• Если матрица вторых частных производных функции f(Х)
(матрица Гессе Н) в стационарной точке Х0 положительно
определена, то Х0 – точка локального минимума функции
f(Х)
• Если матрица вторых частных производных функции f(Х)
(матрица Гессе Н) в стационарной точке Х0 отрицательно
определена, то Х0 – точка локального максимума функции
f(Х)
11

12. Матрица Гессе:

H X
2 f
X , i 1, n, j 1, n
xi x j
2 f
2
x
1
2 f
H x2 x1
....
2
f
x x
n 1
f
x1 x2
2
f
2
x2
2
.....
f
xn x2
2
f
....
x1 xn
2
f
...
x2 xn
....
.....
2
f
.....
2
xn x0 ,.. x0
2
1
n
12

13.

• Матрица Гессе является матрицей квадратичной формы
относительно приращений x1, x2,…, xn.
• Матрица положительно (отрицательно) определена (полу),
если все ее собственные значения положительны
(отрицательны) (могут быть равны нулю).
• Если отрицательно (положительно) полуопределена, то
точка нестрогого экстремума (и необходимые условия). Если
отрицательно (положительно) определена – точка строгого
экстремума (и достаточные условия).
13

14. Критерий Сильвестра

(устанавливает определенность квадратичной формы):
квадратичная форма положительно
определена тогда и только тогда, когда все
главные миноры ее матрицы
положительны, и
отрицательно определена, тогда и только
когда главные миноры переменных
знаков, начиная с «-».
14

15. Порядок решения:

• найти частные производные первого порядка и
приравнять к нулю;
• решить полученную систему, найти стационарные
точки;
• в каждой стационарной точке определить матрицу
Гессе;
• для каждой матрицы Гессе (для каждой стационарной
точки) проверить критерий Сильвестра (установить
определенность матрицы Гессе);
• применить достаточное условие экстремума в
стационарной точке.
15

16. Пример. Квадратичная функция

max f X 8 x 4 x1 x2 5 x
2
1
2
2
f
16 x1 4 x2
x1
16 x1 4 x2
f X
10 x2 4 x1
f
10 x2 4 x1
x2
f X 0
16 x1 4 x2 0
10 x2 4 x1 0
x1 0
x2 0
16

17. Пример. Квадратичная функция

max f X 8 x 4 x1 x2 5 x
2
1
2
2
f
f
f
f
16
4
10
2
2
x1
x1 x2 x2 x1
x2
Матрица Гессе:
16 4
H X
4 10
a11 16 0
( 16)( 10) ( 4)( 4) 160 16 144 0
Точка (0, 0) – точка максимума
17

18.

Найти значения переменных x1 ,..., xn , доставляющих
максимум (минимум) целевой функции
f ( x1 ,..., xn ) max(min)
При этом переменные должны удовлетворять
ограничениям (часто без условий неотрицательности):
gi ( x1 , x2 ,
, xn ) „…
bi
x1 …0; x2 …0;
(i 1, m)
; xn …0
Хотя бы одна из функций f, gi нелинейная.
Отличия от ЗЛП:
1. ОДЗ не обязательно выпуклая.
2. Экстремум не обязан находится на границе ОДЗ.
18

19.

x2
x2
Геометрически задача НП состоит в отыскании точки или
множества точек из допустимого множества, где
достигается поверхность наибольшего (наименьшего)
уровня.
Решение (глобальный максимум или минимум)
существует, если допустимое множество не пустое и
ограниченное. Решение может принадлежать либо границе
(а), либо внутренней части допустимого множества (б).
X*
а)
б)
X*
x1
x1
19

20. Пример:

• Найти экстремумы функции L(x1,x2)=x1+2x2 при
ограничениях x12 + x22 ≤ 25, x1 ≥ 0, x2 ≥ 0.
Максимум достигается в точке А касания окружности
x12 + x22 = 25 и линии уровня x1 + 2x2 = C
А(√5,2√5)
20

21.

Пример:
F ( x1 1)2 ( x2 4)2 min,max
(1)
3 x1 2 x2 7
(2)
10 x1 x2 8
18 x 4 x 12 (3)
1
2
x1 , x2 0
X2
h
3
2
Минимум достигается в центре
окружности:
x*1 1, x*2 4,
f (min) 0
1
X1
Максимум достигается в точке
пересечения ограничений 2 и 3:
18 x1 4(10 x1 8) 12
10 x1 8 x2
x**1 2, x**2 12,
f (max) 65
21

22.

Пример:
F ( x1 3) ( x2 4) min,max
2
2
(1)
3 x1 2 x2 7
(2)
10 x1 x2 8
18 x 4 x 12 (3)
1
2
x1 , x2 0
X2
h
3
Tmin
2
1
X1
( x1 3) 2 ( x2 4) 2 h
2( x1 3) 2( x2 4) x2' 0
x2'
2( x1 3) x1 3
2( x2 4) 4 x2
x1 3 10(4 x2 )
10 x1 x2 8
123 * 422
x
; x2
101
101
324
f (min)
101
*
1
18 x1 4(10 x1 8) 12
10 x1 8 x2
x**1 2, x**2 12,
f (max) 65
22

23.

Общая задача НП очень сложна и до сих пор не имеет
полного решения. Она становится легче, если ограничимся
случаем, когда область ограничений выпукла, а целевая
функция выпукла или вогнута.
Важно: выпуклость и вогнутость функции
определяется только на выпуклом множестве М (ОДЗ)
Выпуклое множество
Невыпуклое множество
Выпуклое множество содержит отрезок, соединяющий две
любые точки этого множества
Пересечение любого числа выпуклых множеств
является выпуклым множеством
23

24.

• Функция f(x) является выпуклой, если для любых х1, х2 и
положительных α, β, в сумме равных 1, имеет место
f ( x1 x2 ) … f (x1 ) f (x2 ).
Функция f(x) является строго выпуклой, если для любых х1, х2
и положительных α, β, в сумме равных 1, при х1≠х2 имеет место
f ( x1 x2 ) f (x1 ) f (x2 ).
Функция f(x) является вогнутой, если для любых х1, х2
и положительных α, β, в сумме равных 1, имеет место
П о в т о р е н и е
f ( x1 x2 ) „ f (x1 ) f (x2 ).
Функция f(x) является строго вогнутой, если для любых х1, х2 и
положительных α, β, в сумме равных 1, при х1 ≠ х2 имеет место
f ( x1 x2 ) f (x1 ) f (x2 ).
Линейные функции одновременно являются и выпуклыми и
вогнутыми, но не являются ни строго выпуклыми, ни строго
вогнутыми
24

25. ПРИЗНАК СТРОГОЙ ВЫПУКЛОСТИ

Дважды дифференцируемая функция f(X) = f(x1, …, хn )
является выпуклой в том и только том случае, когда
f (X )
xi x j 0
i 1 j 1 xi x j
n
n
2
для любых Х и хi, хj, не обращающихся в 0 одновременно.
То есть если в каждой точке ОДЗ второй дифференциал d2f(Х)
есть положительно (полу)определенная квадратичная форма от
дифференциалов независимых переменных, то f (не)строго
выпукла.
Получаем, что для определения выпуклости (вогнутости) можно
воспользоваться критерием Сильвестра.
25

26.

Задача выпуклого программирования
f ( x1 ,..., xn ) min
gi ( x1 , x2 ,
, xn ) bi
i 1, m
f ( x1 ,..., xn ) max
gi ( x1 , x2 ,
, xn ) bi
i 1, m
f(x1,x2, …,хn) – выпуклая на М
f(x1,x2, …,хn) – вогнутая на М
gi(x1,x2, …,хn) - выпуклые на
выпуклом множестве М
gi(x1,x2, …,хn) - выпуклые на
выпуклом множестве М
Задача ЛП является частным случаем задачи выпуклого
программирования
26

27. Свойства выпуклых функций:

1) Если f(X) – выпукла, то функция - f(X) – вогнута.
2) Линии уровня выпуклой или вогнутой функции выпуклы.
3) Если функции fi(X) –выпуклы, i = 1, …, m, то при любых
действительных числах i ≥ 0 функция i fi(X) также является
выпуклой.
4) Если f(X) –выпукла, то для любого числа область решений неравенства
f(X) < является либо выпуклым множеством, либо пустым.
5) Если gi(X) –выпуклые при всех неотрицательных значениях переменных,
то область решений системы неравенств gi(X) ≤ bi , i = 1, ..., m, является
либо выпуклым множеством либо пустым.
6) Выпуклая (вогнутая) функция, определённая на выпуклом множестве,
непрерывна в каждой внутренней точке этого множества.
27

28.

Теорема Вейерштрасса:
если функция f непрерывна на компакте (ограниченном
и замкнутом множестве), то она достигает
минимума и максимума на внутренней
(стационарной) или граничной точке множества.
(Любой локальный экстремум выпуклой функции является глобальным)
Множество точек, на котором достигается глобальный максимум,
выпукло.
28

29.

Если целевая функция f является строго выпуклой
(строго вогнутой) и если область решений системы
ограничений не пуста и ограничена, то задача ВП
всегда имеет единственное решение,
потому что
Всякая дифференцируемая строго выпуклая
(вогнутая) функция имеет не более одной
стационарной точки, которая является точкой
локального и глобального минимума
(максимума).
29

30.

Свойства строго выпуклых функций:
- строго выпуклая функция f имеет не
больше одного локального минимума на М
и ни одного локального максимума.
Глобальный максимум – на границе (если
М – выпуклый компакт).
- если f дифференцируема, строго
выпукла на выпуклой области М и имеет
стационарную точку х0 в М, то х0 является
точкой глобального минимума, притом
единственной.
30

31.

Решение любой задачи математического
программирования (в том числе нелинейного)
можно свести к решению задачи нелинейного
программирования без ограничений.
Для этого необходимо на основе исходной ЗМП
построить функцию Лагранжа.
Два случая:
• задача содержит только ограничения-равенства;
• задача содержит ограничения-неравенства.
31

32.

Задача
нелинейного
программирования
ограничениями-равенствами:
с
f ( x1,..., xn ) max
gi ( x1,..., xn ) bi
(i 1,m)
(m < n)
Метод неопределенных множителей Лагранжа
Введем вектор-строку из m
=( 1,…, m)- множители Лагранжа
новых
переменных
Составим функцию Лагранжа:
m
L f ( x1,..., xn ) i [bi gi ( x1,..., xn )]
i 1
32

33.

Принцип Лагранжа
(необходимое условие экстремума)
Если
- точка экстремума функции
( x10 , x20 ,..., xn0 )
f ( x1 ,...xn )
причем все gi непрерывно дифференцируемы в
окрестности этой точки, и векторы gi ( x10 , x20 ,..., xn0 )
x j
(частные!!!)
линейно
независимы,
тогда
существуют такие множители Лагранжа, не
равные одновременно нулю ( 0 ,..., 0 )
1
что ( x10 , x20 ,..., xn0 , 10 ,..., m0 )
m
-
стационарная точка функции
Лагранжа
L( x ,.., x , ,.., )
1
n
1
m
Условие линейной независимости выполняется, если ОДЗ регулярно по
Слейтеру (имеет хотя бы одну внутреннюю точку)
33

34. Применим необходимое условие экстремума функции

L( x1 ,.., xn , 1 ,.., m )
L
x 0
1
...
L
0
xn
L 0
1
.......
L
0
m
m g ( x ,..., x )
L f ( x1,..., xn )
n
i i 1
0
x j
x j
x j
i
1
L
bi gi ( x1,..., xn ) 0 (i 1,m)
i
( j 1,n)
34

35.

Решив полученную систему
вектор ( x 0 , x 0 ,..., x 0 , 0 ,..., 0 )
1
2
n
1
m
уравнений,
найдем
Из стационарных точек, взятых без координат 1,…, m,
выберем точки, в которых функция f(x) имеет условные
локальные экстремумы. Этот выбор осуществляется, с
применением достаточных условий локального
экстремума.
Если функция f(x) является строго выпуклой (вогнутой),
то она имеет (всегда!) единственный локальный
экстремум – достаточное условие экстремума.
Тогда если получена единственная стационарная точка
функции Лагранжа, то это точка экстремума.
Считаем, что функции f(x1,…,xn)и gi(x1,…,xn) непрерывны и
имеют частные производные, по крайней мере, второго
порядка.
35

36.

Задача
По плану производства продукции предприятию необходимо
изготовить 180 изделий. Они могут быть изготовлены двумя
способами.
При производстве x1 штук первым способом затраты на них
4 x1 x12 рублей.
При производстве
8 x2 x22 рублей.
x2
штук вторым способом затраты на них
Определить: сколько изделий каждым способом нужно
изготовить, чтобы затраты на производство были минимальными.
F 4 x1 x12 8x2 x22 min
x1 x2 180
L 4 x1 x12 8x2 x22 (180 x1 x2 )
x1* 91, x2* 89
L
4 2 x1 0
x
1
L
8 2 x2 0
x2
L
180 x1 x2 0
F 17278 – затраты.
36

37.

Интерпретация множителей Лагранжа
Помимо того, что метод Лагранжа дает решение задачи на
максимум, он позволяет также проанализировать, насколько
оптимальное решение целевой функции чувствительно к изменению
констант ограничений b:
Действительно, пусть bi – переменные и величины xj и i будут
функциями от них. Тогда L(b) f ( x(b)) (b)(b g ( x(b)))
есть тоже функция от b. Дифференцирование по b дает:
T
T
L f x
g x
x
f
g
(b g ( x))T
(b g ( x))T
b x b
x b
b
b x
x
b
Из-за условий первого порядка первые два члена этого выражения
равны 0. Значение функции Лагранжа в точке ( õ10 , õ20 ,..., xn0 , 10 ,..., m0 )
суть оптимальное значение целевой функции.
Следовательно,
L( x0 , 0 ) f 0
b
b
0
37

38.

Экономическая интерпретация множителей
Лагранжа, соответствующих оптимальному
решению, аналогична интерпретации двойственных
оценок ограничений ЗЛП
–
Они показывают величину изменения целевой функции
в расчёте на единицу изменения свободного члена
ограничения, которому соответствует множитель
Лагранжа, в очень малой окрестности оптимума
–
Если ограничение можно рассматривать в качестве баланса
ресурса и максимизируется прибыль, то множитель Лагранжа
в точке оптимума равен оптимальной цене
–
Если найдётся рынок, где ресурс дешевле, то его покупка увеличит
прибыль
–
Если найдётся рынок, где ресурс дороже, то для увеличения
прибыли его следует продать
В отличие от случая ЗЛП, множители Лагранжа (кроме
частных случаев) не обладают свойством устойчивости
Они меняют свои значения даже при сколь угодно малом
изменении свободных членов ограничений
38

39.

Задача
нелинейного
программирования
ограничениями-неравенствами:
с
f ( x1,..., xn ) max
gi ( x1,..., xn ) bi
(i 1,m)
(m < n)
Чтобы применить метод неопределенных множителей
Лагранжа, ограничения-неравенства преобразуем к виду
равенств путем введения дополнительных неотрицательных
переменных s=(s1,…,sm) и запишем ограничения в виде
gi ( x1,..., xn ) si2 bi
(i 1,m)
Введем вектор множителей Лагранжа =( 1,…, m)
Составим функцию Лагранжа:
m
L( x, , s) f ( x1,..., xn ) i[bi gi ( x1,..., xn ) si2]
i 1
39

40.

Необходимым
условием
оптимальности
является неотрицательность вектора ( 10 ,..., m0 )
Действительно, как было показано,
f 0
0
b
Но при увеличении b допустимое множество расширяется,
и, следовательно, максимум целевой функции не может
уменьшиться . Поэтому 0≥0.
Аналогично в задаче минимизации 0≤0.
Если же ограничения заданы в виде равенств, то на знак 0
никаких условий не накладывается.
40

41. Применим необходимое условие экстремума функции

L( x1 ,.., xn , 1 ,.., m , s1 ,.., sm )
m g ( x ,..., x )
L f ( x1,..., xn )
n
i i 1
0
x j
x j
x j
i
1
L
2 i si 0 (i 1,m)
si
L
2
b
g
(
x
,...,
x
)
s
i
i 1
n
i 0 (i 1, m)
i
( j 1,n)
Из двух последних выражений имеем
1. Если i>0, то si=0 и bi – gi(x1, …, xn)=0.
2. Если bi – gi(x1, …, xn)>0, то si>0 и i=0.
Следовательно, можем записать
i (bi gi ( x1,..., xn )) 0 (i 1,m)
41

42.

С учетом неотрицательности вектора
и условия gi ( x1,..., xn ) bi
( 10 ,..., m0 )
(i 1,m)
Получаем условие дополняющей нежесткости
m
i (bi gi ( x1,..., xn )) 0
i 1
42

43.

Условия Куна-Таккера
(необходимые условия экстремума в задаче
с ограничениями-неравенствами):
m g ( x ,..., x )
L f ( x1,..., xn )
i 1
n
0
i
x j
x j
x j
i
1
i (bi g i ( x1,..., xn )) 0 (i 1, m)
g i ( x1,..., xn ) bi (i 1, m)
0 (i 1, m)
i
( j 1,n)
43

44.

Задача нелинейного программирования с ограниченияминеравенствами и ограничениями на знак переменных:
f ( x1,..., xn ) max
gi ( x1,..., xn ) bi
(i 1,m)
(m < n)
x j 0 ( j 1,n)
Перепишем задачу в виде
f ( x1,..., xn ) max
gi ( x1,..., xn ) bi
(i 1,m)
x j 0 ( j 1,n)
Аналогично
предыдущему
ограничения-неравенства
преобразуем к виду равенств путем введения дополнительных
неотрицательных переменных s=(s1,…,sm) и t=(t1,…,tn).
44

45.

Перепишем задачу в виде
f ( x1,..., xn ) max
gi ( x1,..., xn ) si2 bi
(i 1,m)
(m < n)
x j t 2j 0 ( j 1,n)
Введем множители Лагранжа =( 1,…, m) и =( 1,…, n)
Составим функцию Лагранжа:
m
L( x, s,t, , ) f ( x1,..., xn ) i [bi gi ( x1,..., xn ) si2 ]
i 1
n
j [ x j t 2j ]
j 1
45

46.

Запишем
условия
Куна-Таккера
:
gi ( x1,..., xn )
L f ( x1,..., xn )
i
j 0 ( j 1, n)
x j
x j
x j
i
1
i (bi g i ( x1,..., xn )) 0 (i 1, m)
g i ( x1,..., xn ) bi (i 1, m)
i 0 (i 1, m)
0 ( j 1, n)
j
x 0 ( j 1, n)
• Исключив из этих
j
уравнений , получим
x 0 ( j 1, n)
j j
46
m

47. Условия Куна-Таккера:

- Условия первого порядка:
f ( X ) m gi ( X )
i
0 ( j 1,n)
x j i 1
x j
gi ( X ) bi (i 1,m)
- Условия дополняющей нежесткости:
f ( X ) m gi ( X )
i
) x j 0
(
x j
j 1 x j
i 1
n
x j 0 ( j 1,n)
m
i (bi gi ( X )) 0
i 1
i 0 (i 1,m)
В случае задачи минимизации знаки неравенств в первой и последнем из этих
условий заменяются на противоположные
Точка, удовлетворяющая условиям Куна-Таккера – точка Куна-Таккера
47

48.

Теорема Куна-Таккера
любой из существующих оптимумов функции f
соответствует точке Куна-Таккера функции Лагранжа
Если функция f строго выпукла, точек Куна-Таккера не более
одной.
Тогда если точка Куна-Таккера имеется, то в ней находится
оптимум (условия Куна-Таккера являются необходимыми и
достаточными).
Для невыпуклой задачи условия Куна-Таккера могут не иметь
решения
Достаточность условий Куна-Таккера:
• Проверить матрицу Гессе:
• Если положительно определённая в стационарной
точке, то – минимум. Если отрицательно определённая
в стационарной точке, то – максимум.
48

49.

По теореме Куна-Таккера, решение задачи выпуклого
программирования находится среди седловых точек
функции Лагранжа целевой функции.
По дифференциальному варианту теоремы КунаТаккера, в седловой точке выполняются условия КунаТаккера.
49