Выигрышные стратегии

1. ВЫИГРЫШНЫЕ СТРАТЕГИИ

2. ЗАДАНИЕ

Два игрока, Петя и Ваня, играют в следующую игру. Перед
игроками лежат две кучи камней. Игроки ходят по очереди, первый
ход делает Петя. За один ход игрок может добавить в одну из куч
(по своему выбору) один камень или увеличить количество камней
в куче в два раза. Например, пусть в одной куче 10 камней, а в
другой 7 камней; такую позицию в игре будем обозначать (10, 7).
Тогда за один ход можно получить любую из четырёх позиций: (11,
7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого
игрока есть неограниченное количество камней.

3.

Игра завершается в тот момент, когда суммарное количество
камней в кучах становится не менее 73. Победителем считается
игрок, сделавший последний ход, т.е. первым получивший такую
позицию, что в кучах всего будет 73 камня или больше.
Будем говорить, что игрок имеет выигрышную стратегию, если он
может выиграть при любых ходах противника. Описать стратегию
игрока – значит описать, какой ход он должен сделать в любой
ситуации, которая ему может встретиться при различной игре
противника. Например, при начальных позициях (6, 34), (7, 33), (9,
32) выигрышная стратегия есть у Пети. Чтобы выиграть, ему
достаточно удвоить количество камней во второй куче.

4.

Задание 1. Для каждой из начальных позиций (6, 33), (8, 32) укажите, кто
из игроков имеет выигрышную стратегию. В каждом случае опишите
выигрышную стратегию; объясните, почему эта стратегия ведёт к
выигрышу, и укажите, какое наибольшее количество ходов может
потребоваться победителю для выигрыша при этой стратегии.
Задание 2. Для каждой из начальных позиций (6, 32), (7, 32), (8, 31)
укажите, кто из игроков имеет выигрышную стратегию. В каждом случае
опишите выигрышную стратегию; объясните, почему эта стратегия ведёт
к выигрышу, и укажите, какое наибольшее количество ходов может
потребоваться победителю для выигрыша при этой стратегии.
Задание 3. Для начальной позиции (7, 31) укажите, кто из игроков имеет
выигрышную стратегию. Опишите выигрышную стратегию; объясните,
почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее
количество ходов может потребоваться победителю для выигрыша при
этой стратегии. Постройте дерево всех партий, возможных при
указанной Вами выигрышной стратегии. Представьте дерево в виде
рисунка или таблицы.

5. ОБЩИЕ ЗАМЕЧАНИЯ

1. У нас есть две кучки камней и два игрока: первый (Петя) и
второй (Ваня).
2. Игроки ходят по очереди.
3. За ход в любую из кучек можно либо добавить один камень,
либо увеличить количество камней в кучке в два раза.
4. Как только суммарно в кучке стало 73 или более камня, игра
заканчивается.
5. Тот, кто ходил последним, выиграл.

6. РЕШЕНИЕ №1

Первый игрок очевидно в один ход выиграть не может, так как что бы он не делал, суммарно 73 не
будет. Самое "большое" действие, которое он может сделать, — это увеличить в 2 раза количество
камней во второй кучке, сделав их 66. Но (6, 66) — это 72 камня, а не 73.
Первый может сделать потенциально четыре действия: прибавить 1 к первой кучке, увеличить в 2 раза
количество камней в первой кучке, прибавить 1 ко второй кучке, увеличить в 2 раза количество камней
во второй кучке. Посмотрим, к чему это приведёт:
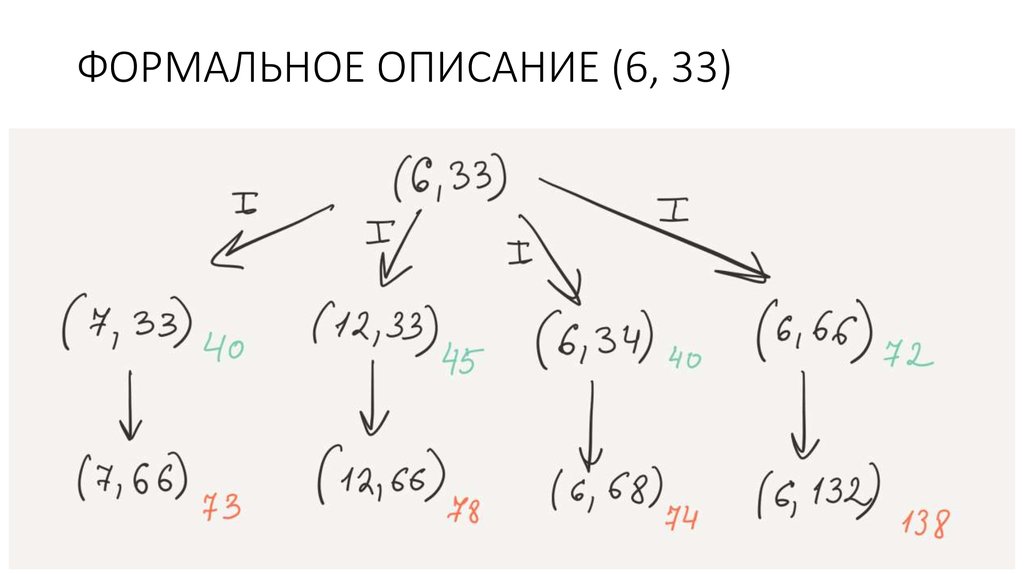
(6,33) -> (7,33). В этом случае второй игрок может увеличить в 2 раза количество камней во второй кучке.
Получим (7, 66). Суммарно — 73. Значит, второй выигрывает.
(6,33) -> (12, 33). В этом случае второй игрок может увеличить в 2 раза количество камней во второй
кучке. Получим (12, 66). Суммарно — 78. Значит, второй выигрывает.
(6,33) -> (6,34). В этом случае второй игрок может увеличить в 2 раза количество камней во второй кучке.
Получим (6, 68). Суммарно — 74. Значит, второй выигрывает.
(6,33) -> (6,66). В этом случае второй игрок может увеличить в 2 раза количество камней во второй кучке.
Получим (6, 132). Суммарно — 138. Значит, второй выигрывает.
Итого: как бы себя не вёл первый игрок, второй выиграет и в один ход.
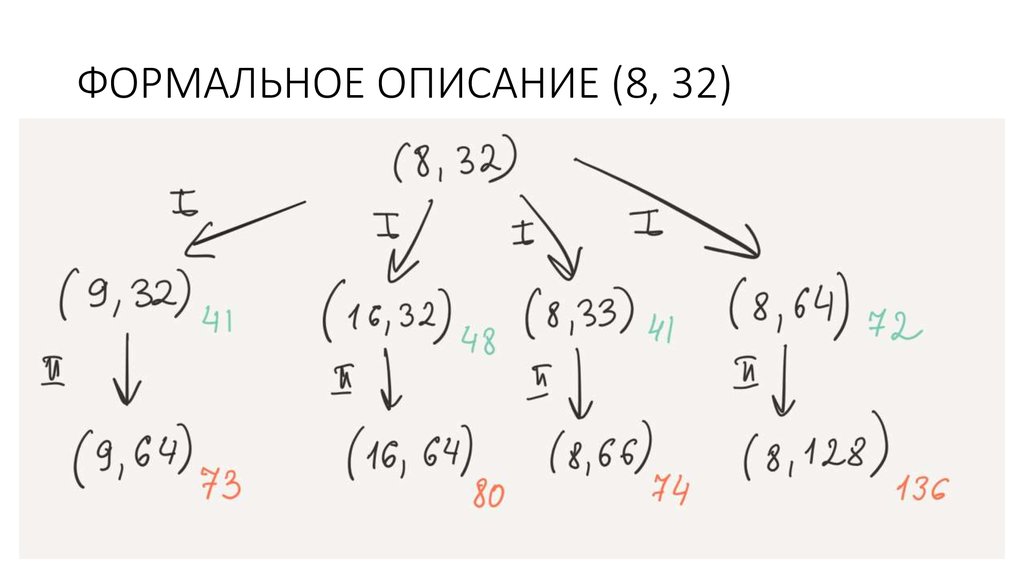
Аналогично решается и с (8,32).

7. ФОРМАЛЬНОЕ ОПИСАНИЕ (6, 33)

8. ФОРМАЛЬНОЕ ОПИСАНИЕ (8, 32)

9. РЕШЕНИЕ №2

Рассмотрим начальную позицию (6,32). Заметим, что она близка к (6,33)
из Задания 1. В Задании 1 мы выяснили, что в позиции (6, 33)
выигрывает второй, причём в один ход. Можно это условие
переформулировать: в позиции (6,33) выигрывает в один ход тот,
кто не ходит (то есть, ходит вторым). Или, иными словами, тот, кто ходит,
проигрывает в один ход.
В позиции (6,32) выигрывает первый в два хода. Докажем это. Первым
своим ходом Петя добавляет +1 ко второй кучке. Таким образом,
получается позиция (6,33). Как мы выяснили ранее, в позиции (6,33) тот,
кто ходит, проигрывает. В нашем случае будет ход Вани. Поэтому Ваня
проиграет в один ход. При этом Пете придётся сделать в сумме два хода:
первый (добавить 1 камень во вторую кучку) + второй ход в
соответствии с Деревом партий в Задании 1, действуя по стратегии Вани.

10.

Аналогично в позиции (7, 32). Петя своим первым ходом добавляет
+1 камень в первую кучку, получая позицию (8, 32). В этой позиции
согласно тем же рассуждениям, тот, кто ходит, проигрывает. Будет
ход Вани, поэтому Ваня проиграет. Выигрышная стратегия Пети
заключается в следующем: Петя добавляет +1 камень в первую
кучку, а затем следует стратегии Вани из Задания 1.
Аналогично в позиции (8, 31). Петя своим первым ходом добавляет
+1 камень во вторую кучку, получая позицию (8, 32). В этой
позиции согласно тем же рассуждениям, тот, кто ходит,
проигрывает. Будет ход Вани, поэтому Ваня проиграет.
Выигрышная стратегия Пети заключается в следующем: Петя
добавляет +1 камень во вторую кучку, а затем следует стратегии
Вани из Задания 1.

11.

Заметим, что из ситуации (7, 31) очень легко попасть либо в
ситуации (8, 31) и (7, 32), в которых, согласно предыдущему
Заданию, тот, кто ходит, выигрывает, либо в ситуации (14, 31) и (7,
62), в которых тот, кто ходит, может выиграть в один ход, увеличив
в два раза количество камней во второй кучке. Таким образом,
получается, что у Вани должна быть выигрышная стратегия. При
этом он может выиграть как в 2 хода (первые два случая), так и в
один ход (вторые два случая).
Дерево решений построить самостоятельно.