Эпохи вычислительной техники

1. Эпохи вычислительной техники

кафедра ЮНЕСКО по НИТ
1

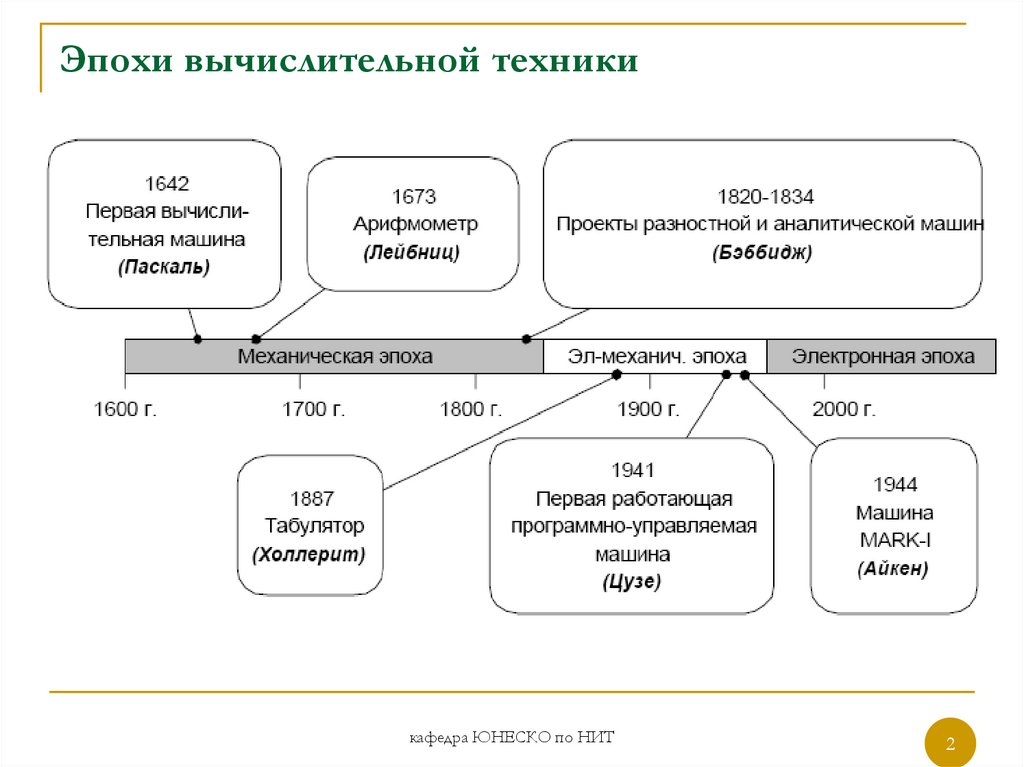
2. Эпохи вычислительной техники

кафедра ЮНЕСКО по НИТ
22

3. Домеханическая эпоха

Информатика
кафедра ЮНЕСКО по НИТ
3

4. Абак

MCMXCVI + CCLXIV = ?
Уже
древние
римляне
располагали
простейшим
приспособлением для ускорения счета, основанным на
позиционной системе счисления, который назывался абак.
кафедра ЮНЕСКО по НИТ
44

5. Абак

Абак
представляет
собой
дощечку,
разделенную
вертикальными перегородками на несколько отделений,
соответствующим
отдельным
разрядам
числа
в
позиционной системе счисления.
В отделениях помещались камешки (по латыни «камешек» —
«calculus», отсюда слова «калькуляция», «калькулятор»).
Число их в отделении равно значению разряда и может
меняться (в десятичной системе счисления) от 0 до 9.
Сложение чисел производится путем поразрядного
добавления камешков, при переполнении отделения оно
очищается и делается перенос единицы в следующий
разряд.
Впервые появился в Древнем Вавилоне ок. 3 тыс. до н. э.
кафедра ЮНЕСКО по НИТ
55

6. Абак (продолжение)

Древнеримский абак
кафедра ЮНЕСКО по НИТ
66

7. Абак (продолжение)

Реконструкция римского абака
кафедра ЮНЕСКО по НИТ
77

8. Счеты

Арабские купцы разнесли абак по
всему миру.
Китайцы нанизали камешки на спицы,
вставили их в деревянную раму и
повернули все на 90 градусов.
В таком виде абак в XVI веке попал в
Россию и стал называться русскими
счетами.
Русские счеты
кафедра ЮНЕСКО по НИТ
88

9. Логарифмическая линейка

Логарифмическая линейка появилась в первой трети XVII
века, вскоре после того, как в 1614 году шотландский
барон Джон Непер (Nepier, John; 1550-1617) опубликовал
свою первую книгу «Magnifici logarithmorum cannonis
discriptio».
кафедра ЮНЕСКО по НИТ
99

10. Логарифмическая линейка

Эту логарифмическую линейку двести выпускников университета Джона
Пердью (Вест-Лафайет, штат Индиана) подарили своей alma mater (2004 г.)
кафедра ЮНЕСКО по НИТ
10

11. Логарифмическая линейка (продолжение)

Принцип действия логарифмической линейки основан на
основном правиле логарифмов:
log(a•b) = log(a) + log(b),
что позволяет заменить операцию умножения сложением, а
операцию деления — вычитанием. Сложение (вычитание)
производится путем простого перемещения двух реек
Принцип действия
логарифмической линейки
a=2, b=3, a•b=6
кафедра ЮНЕСКО по НИТ
11
11

12. Цифровые и аналоговые вычисления

Цифровые (дискретные) и аналоговые вычисления — это
две постоянно сосуществующие и конкурирующие ветви
математики. Математика древнего мира была в
подавляющей
степени
связана
с
аналоговыми
построениями. Строго говоря, циркуль и линейка — это
тоже древнейшая аналоговая вычислительная машина.
С изобретением символических алгоритмов арифметики
роль аналоговых вычислений стала ослабевать, так как
цифровые методы способны обеспечить более высокую
точность вычислений. Обычная логарифмическая
линейка, например, дает результат с точностью до 1 — 0.1
% (2—3 знаков после запятой), причем ошибка быстро
накапливается с увеличением сложности вычислений.
кафедра ЮНЕСКО по НИТ
12
12

13. Цифровые и аналоговые вычисления (продолжение)

Однако не всегда и не везде нужна астрономическая
точность, поэтому, параллельно с цифровой,
развивалась и аналоговая вычислительная техника.
В XIX и XX веках для аналоговых вычислений
использовались самые различные физические процессы:
механические,
гидравлические,
после
изобретения радиоламп и транзисторов —
электронные.
Еще в 1960-х годах популярность аналоговых электронных
вычислительных машин была сравнима с цифровыми, их
изучение было обязательным на всех технических
факультетах.
кафедра ЮНЕСКО по НИТ
13
13

14. Цифровые и аналоговые вычисления (продолжение)

В 1930 г. профессор Массачусетского технологического
института (МТИ) Ванневар Буш (Boosh, Vannevar; 18901974) построил «дифференциальный анализатор» —
большую механическую аналоговую машину, способную
решать сложные дифференциальные уравнения.
Он представлял собой сложнейшую систему реек,
шестеренок, валиков размером с целую комнату.
Обязанности оператора на этой машине выполнял
молодой аспирант Клод Шеннон — будущий автор теории
информации.
С тех пор МТИ стал крупнейшим центром исследований в
области вычислительной техники и информатики.
кафедра ЮНЕСКО по НИТ
14
14

15. Цифровые и аналоговые вычисления (продолжение)

После
изобретения
микропроцессоров (1970-е годы),
когда цифровые ЭВМ резко
уменьшились в габаритах и
подешевели, аналоговые ЭВМ
сильно сдали в конкурентной
борьбе с ними.
Стало проще перевести аналоговый
сигнал в цифровую форму,
выполнить
требуемые
вычисления, а на выходе обратно
преобразовать
результат
в
физическую величину.
По такому пути пошли звукозапись,
и телевидение.
кафедра ЮНЕСКО по НИТ
Большая аналоговая
вычислительная машина
(1960-е годы)
15
15

16. Цифровые и аналоговые вычисления (продолжение)

Считается
спорным
утверждение,
что
аналоговые
вычисления вытеснены навсегда.
Некоторые объекты, например, графические образы,
являются исключительно трудными для символьной
обработки.
Даже самые мощные цифровые процессоры, вооруженные
современными
алгоритмами,
пасуют
перед
распознаванием рукописного текста, а малограмотный
человек легко решает эту задачу.
кафедра ЮНЕСКО по НИТ
16
16

17. Цифровые и аналоговые вычисления (продолжение)

Установлено, что в человеческом мозгу одно полушарие
(левое) подобно цифровой вычислительной машине
оперирует со знаками и абстрактными понятиями. Правое
же полушарие отвечает за образное, неструктурированное,
аналоговое мышление. Только совместная работа обоих
полушарий делает мозг таким, как он есть —
недоступным для конкуренции со стороны компьютеров в
обозримом будущем.
Поэтому построение цифро-аналоговых вычислительных
машин, представляется весьма перспективными для XXI
века.
кафедра ЮНЕСКО по НИТ
17
17