Similar presentations:
מדדי פיזור לשילוב
1.
תיאור התפלגות-מדדי פיזוראו
על מה שמדדי הנטייה למרכז לא מספרים
לנו!.....
•טווח/תחום )(R-range
•טווח/תחום בין רבעוני()IQR-inter-quartile range
•שונות ()variance
•סטיית תקן ()standard deviation
2.
הצגת הבעיה:• מדדי הנטייה למרכז (שכיח ,חציון ,ממוצע) מתארים
את הערך ה"טיפוסי" בקבוצה ,אך אינם מתארים
את המידה שבה יש חריגות מאותו ערך טיפוסי!
3.
דוגמא:• לפניכם תיאור של שתי התפלגויות (א,ב) .חישבו בהן את
המדדים :שכיח ,חציון ,וממוצע .
3
•
ב
א
4 ,3 ,3 ,2
3 ,3 ,3 ,3
2
שכיחות
3
3
2
1
1
4
3
2
1
4
3
2
1
שכיחות
4
4
4.
האם הקבוצות זהות בהרכבן?ב
א
4 ,3 ,3 ,2
3 ,3 ,3 ,3
2
שכיחות
3
3
2
1
1
4
3
2
1
4
3
2
1
שכיחות
4
4
5.
הגדרה כללית של מדדי פיזור:• מדדים סטטיסטיים המשקפים את מידת פיזורם
של הערכים (=התצפיות) בהתפלגות .למשל:
ציונים בכיתה
• מדד פיזור קובע את מידת ההומוגניות או
ההטרוגניות של ההתפלגות:
הומוגניות – עד כמה קיים דמיון בין הנתונים ,עד
כמה הם מקובצים סביב הממוצע.
הטרוגניות – עד כמה קיימים הבדלים ושוני בין
הנתונים ,עד כמה הם מפוזרים על פני הטווח.
6.
מדדי פיזור• מדדי הפיזור מתארים את המידה שבה האיברים בקבוצה שונים
אלה מאלה.
• במסגרת הקורס נכיר ארבעה סוגים מרכזיים של מדדי פיזור:
– טווח/תחום )(range
– תחום בין-רבעוני ()inter-quartile range
– שונות ()variance
– סטיית תקן ()standard deviation
הערה :קיימים מדדים נוספים עליהם לא נדבר בקורס זה :אחוז שגיאה -זהו אחוז המקרים בהם
איבר שונה מן השכיח של הקבוצה שלו .ניתן לחישוב עבור כל סולמות המדידה-אך אינו שימושי
במיוחד!
7.
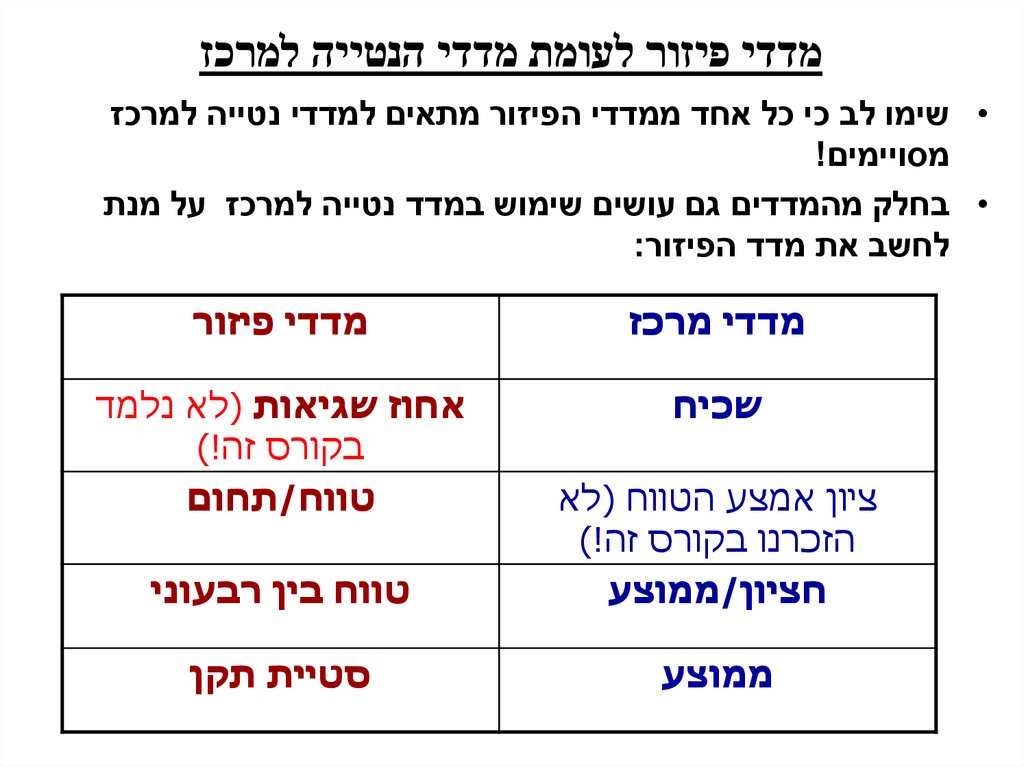
מדדי פיזור לעומת מדדי הנטייה למרכז• שימו לב כי כל אחד ממדדי הפיזור מתאים למדדי נטייה למרכז
מסויימים!
• בחלק מהמדדים גם עושים שימוש במדד נטייה למרכז על מנת
לחשב את מדד הפיזור:
מדדי מרכז
מדדי פיזור
שכיח
אחוז שגיאות (לא נלמד
בקורס זה!)
טווח/תחום
ציון אמצע הטווח (לא
הזכרנו בקורס זה!)
חציון/ממוצע
טווח בין רבעוני
ממוצע
סטיית תקן
8.
טווח/תחום )(R-range9.
טווח/תחום ()Range• הטווח נותן אמדן גס למידת הפיזור של המשתנים.
המדד מציין את הטווח שעליו מתפרסים הערכים
בקבוצה (=התצפיות בהתפלגות).
• הטווח הוא ההפרש בין הערך הגבוה ביותר
בקבוצה (=התצפית הגדולה ביותר) לבין הערך
הנמוך ביותר (התצפית הנמוכה ביותר)
R Max Min
• דוגמא :בסדרת המספרים הבאה:
– הטווח הוא104 – 1 = 103 :
104 ,55 ,12 ,7 ,1
10.
מאפייני הטווח/תחום•
•
הטווח משמש לחישוב מהיר ונוח לערכי ההתפלגות.
הטווח לוקח בחשבון רק את שני הערכים הקיצוניים-כלומר מתבסס
על קצוות ההתפלגות ,תוך התעלמות ממרכז ההתפלגות-פיזור
הערכים בסדרה הסטטיסטית.
הטווח ,בדומה למדד המרכזי אמצע הטווח ,אינו "מתחשב" בפיזור
הנתונים וכן במספרם
הטווח מושפע מערכים קיצוניים!
דוגמא :בסדרה 100 ,50 ,50 ,50 ,50 ,50 ,50 ,50 ,1הטווח (100-
)1=99אינו משקף את העובדה שכלל אין פיזור במרבית ההתפלגות!
ביטוי של החסרון של הטווח :קיומם של ערכים חריגים,קיצוניים-יוצא
שהם קובעים את מידת הפיזור!
ניתן לחישוב עבור משתני רווח ומנה .עבור משתנה סדר ניתן רק
לציין את הערכים שבינייהם ממוקמות כל התצפיות בקבוצה
•
הטווח אינו משמש לחישובים סטטיסטיים מתקדמים!
•
•
•
•
•
(דוגמא :באוסף חולצות בגדלים ,XXL ,XL ,L ,M ,S ,S :ניתן רק לומר שהגדלים הקיימים הם
בין Sלבין )XXL
11.
)variance( שונות12.
• השונות משקפת את המידה שבה האיברים בקבוצהשונים מן הממוצע (סטיות מן הממוצע).
• למשל ,בקבוצה [ ]9 ,7 ,5 ,3 ,1הממוצע הוא .5
–
–
–
–
–
1שונה מ 5-ב4-
3שונה מ 5-ב2-
5שונה מ 5-ב0-
7שונה מ 5-ב-2-
9שונה מ 5-ב-4-
• השונות לוקחת בחשבון סטיות אלו מן הממוצע כדי לתת
אמדן למידת הפיזור של האיברים בקבוצה.
• סיכום כלשהו של הסטיות מן הממוצע מהווה אמדן
למידת הפיזור של המשתנה!
• אך החיים לא כ"כ פשוטים!....
13.
מה]9 ,קורה כאשר מסכמים את הסטיות?בקבוצה [7 ,5 ,3 ,1
הממוצע הוא .5
=5
ממוצע
1שונה מ 5-ב4-
3שונה מ 5-ב2-
5שונה מ 5-ב0-
7שונה מ 5-ב-2-
9שונה מ 5-ב-4-
-2
-1
1
2
1
2
3
4
5
6
7
8
9
בשל אופן חישוב הממוצע ,סכום רגיל של הסטיות
מן הממוצע יהיה תמיד ! 0
14.
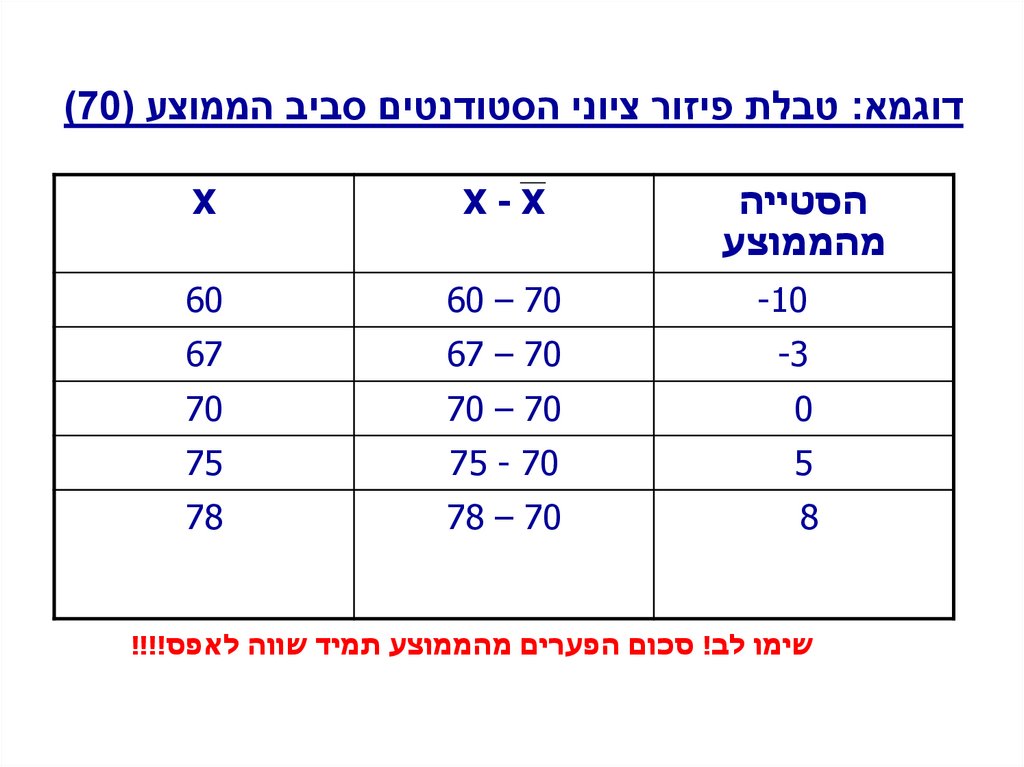
דוגמא :טבלת פיזור ציוני הסטודנטים סביב הממוצע ()70X-X
X
הסטייה
מהממוצע
-10
60 – 70
60
-3
67 – 70
67
0
70 – 70
70
5
75 - 70
75
8
78 – 70
78
שימו לב! סכום הפערים מהממוצע תמיד שווה לאפס!!!!
15.
פתרון לחישוב השונות (התמודדות עם הבעיה שסכוםרגיל של הסטיות מן הממוצע יהיה תמיד :) 0
• על מנת לסכם את הסטיות ,ניתן לחשב את סכום ריבועי הסטיות
מן הממוצע .הסיבה :ריבוע של מס' שלילי הינו מספר חיובי! למשל
(-5)2=25 :וגם (5)2=25
• בדוגמא :
[]9 ,7 ,5 ,3 ,1
(9 5) (7 5) (5 5) (3 5) (1 5) (4) (2) (0) ( 2) ( 4) 16 4 0 4 16 40
2
2
2
2
2
2
2
2
2
2
• כדי לקבל אמדן לסטייה הממוצעת ,ניתן לחלק את הסכום שקיבלנו
( )40במספר האיברים בקבוצה (40/5=8 : )5
16.
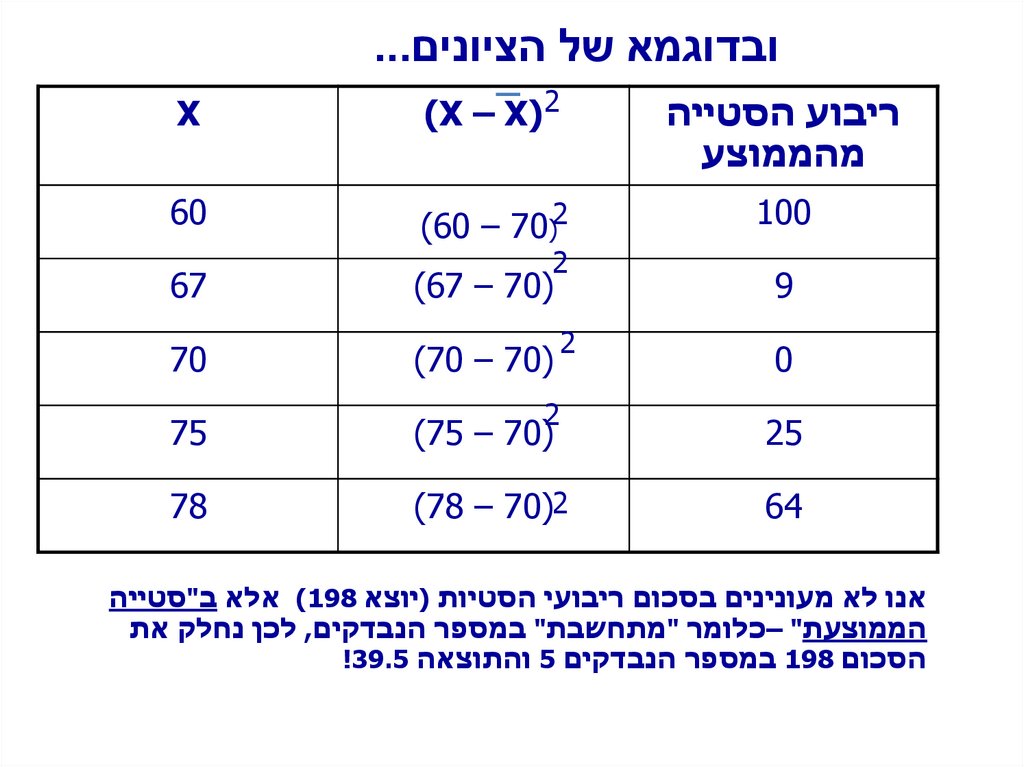
ובדוגמא של הציונים...ריבוע הסטייה
מהממוצע
(X – X)2
X
100
)60 – 70(2
60
9
()67 – 70
67
)(70 – 70
70
25
2
()75 – 70
75
64
)78 – 70(2
78
0
2
2
אנו לא מעונינים בסכום ריבועי הסטיות (יוצא )198אלא ב"סטייה
הממוצעת" –כלומר "מתחשבת" במספר הנבדקים ,לכן נחלק את
הסכום 198במספר הנבדקים 5והתוצאה !39.5
17.
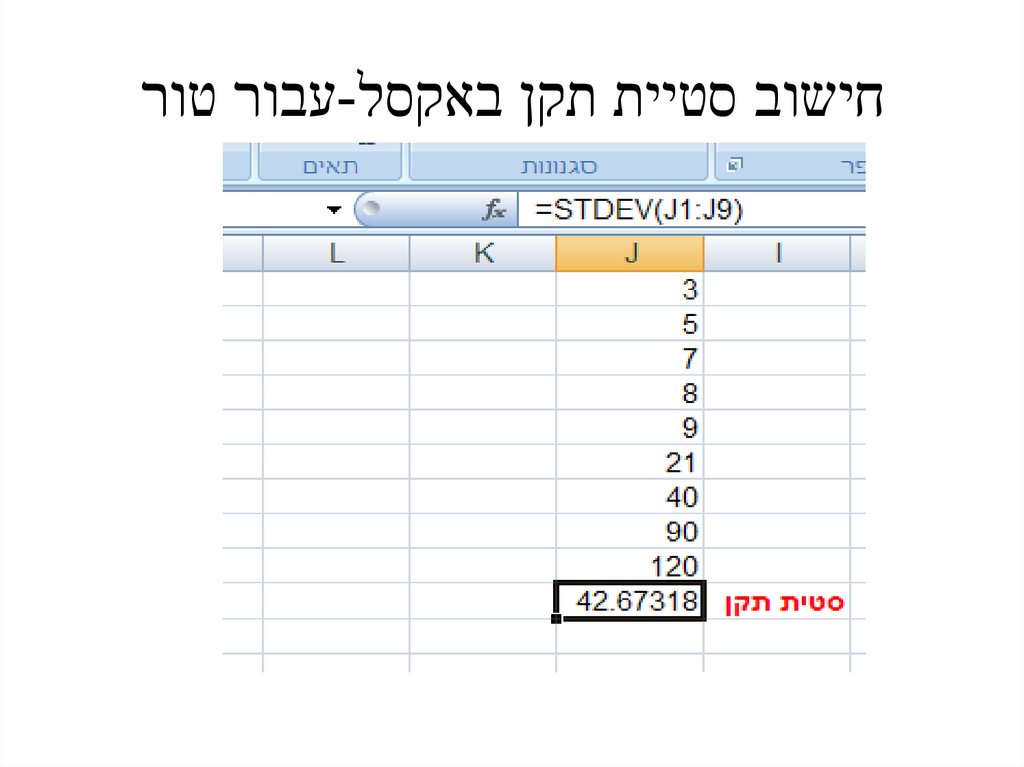
חישוב שונות באקסל18.
הרחבה למתעניינים-לא תתבקשו לבצע ידנית בבחינה!נוסחא לחישוב השונות
• השונות ( )s2היא אם כך:
סכום ()S
הסטיות המרובעות ( (2ממוצע) – ( xiתצפית))
חלקי מספר התצפיות בקבוצה ()n
2
)
i
(x
i
n
s
2
19.
המעבר משונות לסטיית תקן-הצגת הבעיה• השונות -משמשת מדד פיזור בחישובים
סטטיסטיים מתקדמים .אך יש כאן שתי
בעיות:
א .הערך של השונות גדול יחסית מהפערים בין
הנתונים ,בגלל החישוב של ריבועי הפערים.
ב .יחידות המדידה הן בריבוע ולכן לא ניתן להשוותם
לממוצע! (לדוגמא :מדדנו גובה במטרים,הממוצע
יהיה במטרים,אך השונות תהיה במטרים בריבוע!)
• פתרון כדי לקרב את הערך של המדד עד
כמה שאפשר לסדרי הגודל של הפערים וגם
ע"מ לחזור ליחידות המדידה המקוריות" -נוציא
שורש" ריבועי מהערך המספרי של השונות-
זאת סטיית התקן !
20.
-סטית התקןstandard
STDEV=deviation
21.
• השונות מהווה את הסטייה הריבועית הממוצעת מן הממוצע.• על מנת לקבל אמדן לסטייה הממוצעת (שימו לב-ולא הסטייה
הריבועית הממוצעת!) ,מחשבים את שורש השונות .זו סטיית
התקן:
תצפית בודדת
2
סטיית התקן
)
ממוצע
i
(x
i
n
s s
2
גודל המדגם
• סטית התקן מהווה אמדן למידה שבה הערכים בקבוצה שונים
מממוצע הקבוצה!
• כלומר :זהו מדד המשקף את ממוצע הפערים של
הסטיות מהממוצע
22.
שלבים בחישוב סטיית תקן(מבוצע ע"י המחשב-לא לדאוג!)
א .חישוב הממוצע
ב .חישוב הפער בין כל ציון לבין הממוצע
והעלאתו בריבוע
ג .חישוב סכום הריבועים
ד .חלוקה למספר הנבדקים
ה .הוצאת שורש ריבועי
23.
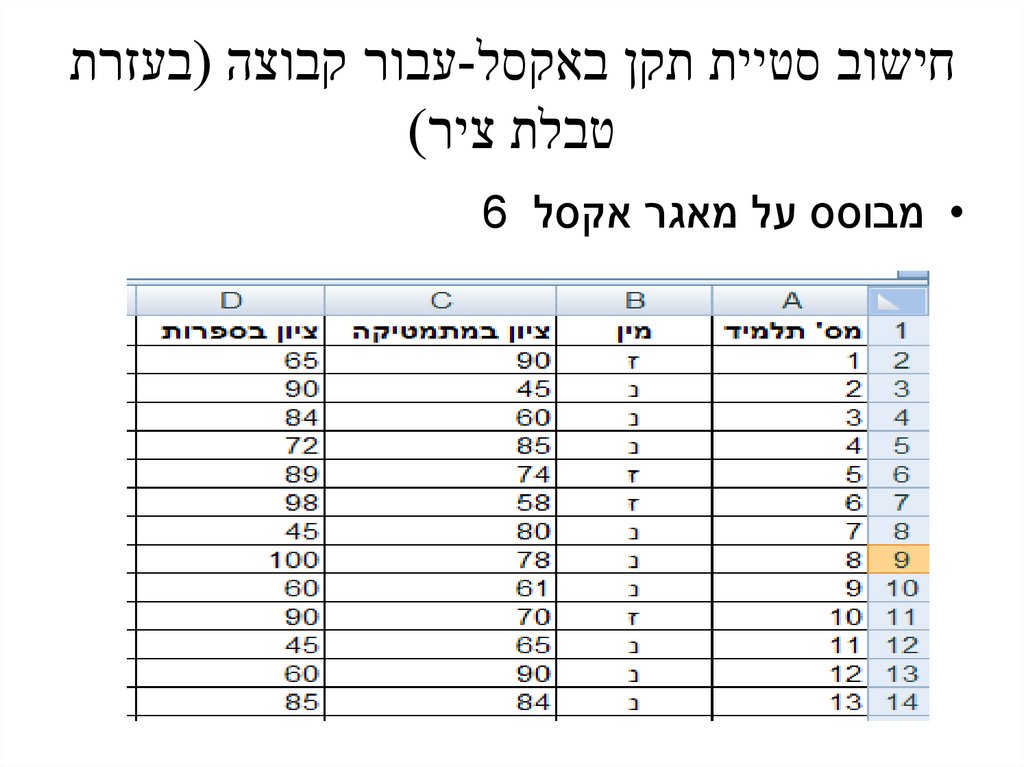
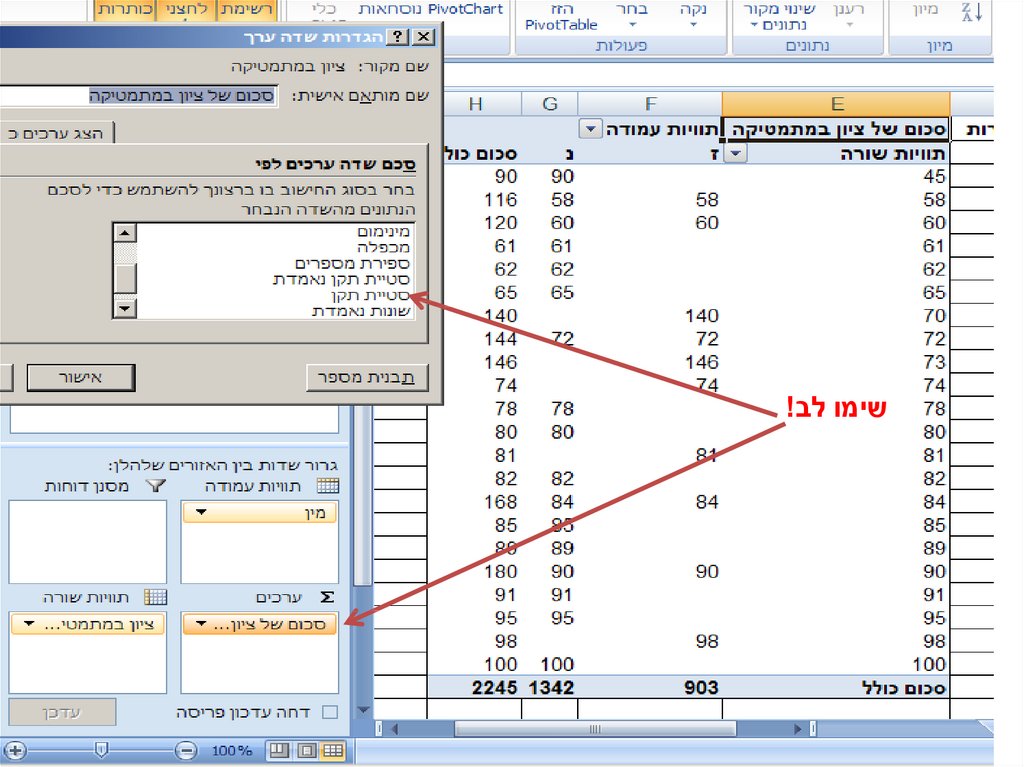
חישוב סטיית תקן באקסל-עבור טור24.
חישוב סטיית תקן באקסל-עבור קבוצה (בעזרתטבלת ציר)
• מבוסס על מאגר אקסל 6
25.
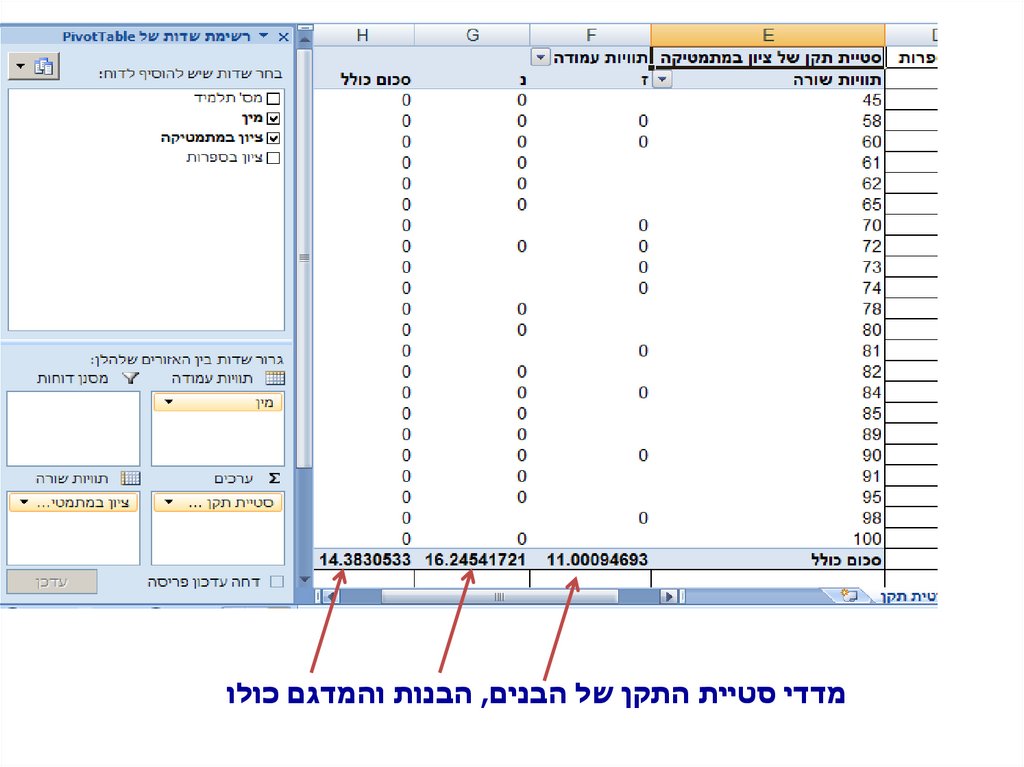
שימו לב!26.
מדדי סטיית התקן של הבנים ,הבנות והמדגם כולו27.
מאפיינים כלליים של השונות וסטיית התקן•
•
•
•
•
•
ניתנים לחישוב עבור משתני רווח ומנה בלבד!
משמשים להסקה סטטיסטית.
כמו כל מדדי הפיזור ,הם מהווים אמדן למידת
ההטרוגניות/הומוגניות של הקבוצה.
נלקחים בחשבון כל האיברים בקבוצה.
ערכים קיצוניים (שלהם סטייה גבוהה מן הממוצע) מקבלים משקל
יתר (בגלל ההעלאה של הסטיות בריבוע)!
המשמעות של כך ,היא שגם מספר מצומצם של ערכים
קיצוניים יכולים להוביל לכך שתתקבלנה שונות וסטיית תקן
גבוהות ,ועל כן ,כביכול ,עדות להטרוגניות גבוהה! אז זהירות
בהסקת מסקנות מרחיקות לכת!
28.
המשמעויות והמאפיינים של סטית התקן29.
א .גודל סטיית התקןסטיית תקן גדולה -הטרוגניות של הנתונים – פיזור גדול!
סטיית תקן קטנה -הומוגניות של הנתונים -פיזור קטן!
ב .סטיית התקן נמדדת ביחידות המדידה של המשתנה.
דוגמא:
המשתנה "משקל" נמדד בק"ג,
סטיית התקן אף היא נמדדת בק"ג.
30.
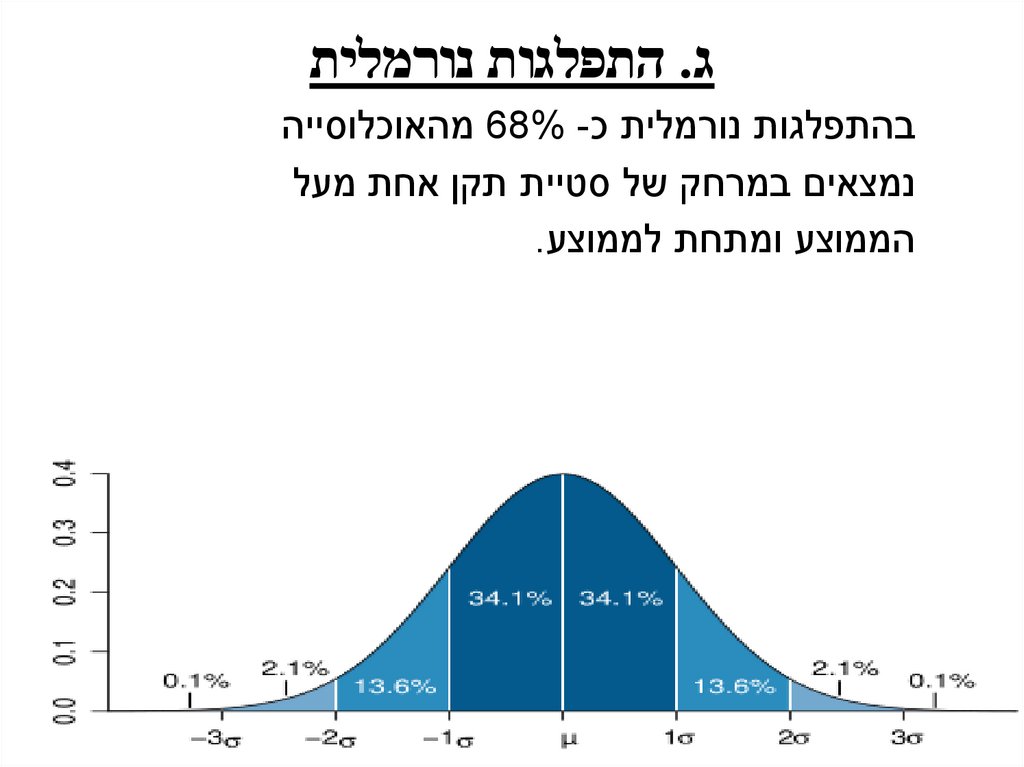
ג .התפלגות נורמליתבהתפלגות נורמלית כ 68% -מהאוכלוסייה
נמצאים במרחק של סטיית תקן אחת מעל
הממוצע ומתחת לממוצע.
31.
ד .ישנה זיקה בין "טווח" לגודל של סטיית התקן: .1בהתפלגות נורמלית סטיית התקן שווה לשישית מטווח הנתונים.
דוגמא:
אם בהתפלגות נורמלית ,הטווח שווה ל ,60 -אז
סטיית התקן שווה בערך ל 1/6( 10 -של .)10 = 60
.2בהתפלגות שאינה נורמלית ,סטיית התקן שווה :בין שליש מהגודל של
טווח הערכים לרבע ממנו.
דוגמא:
אם הטווח שווה ל ,22 -אז
סטיית התקן יכולה לקבל ערכים בין 5.5ל 1/3( 7 -מהטווח שווה ל ,7 -רבע ממנו שווה ל-
.)5.5
שימו לב! מדובר בהערכה של הגודל של סטיית התקן ,את הערך המדויק מקבלים תמיד על ידי
חישוב!
32.
.3כאשר כל הנתונים שווים זה לזהסטיית התקן הנה מינימלית -שווה לאפס .במצב זה
המשתנה "קבוע" (כולם בני 15או בגובה .)169
.4כאשר קיימים שני נתונים במדגם ,סטיית התקן הנה
המקסימלית ,ואינה יכולה לעלות על מחצית טווח
הערכים.
דוגמא :סטיית התקן של שני ציונים 68ו2 = 72 -
הסבר :הטווח שווה ל ,)72 – 68( 4סטיית התקן שווה ל 2
( 1/2מ)4 -
33.
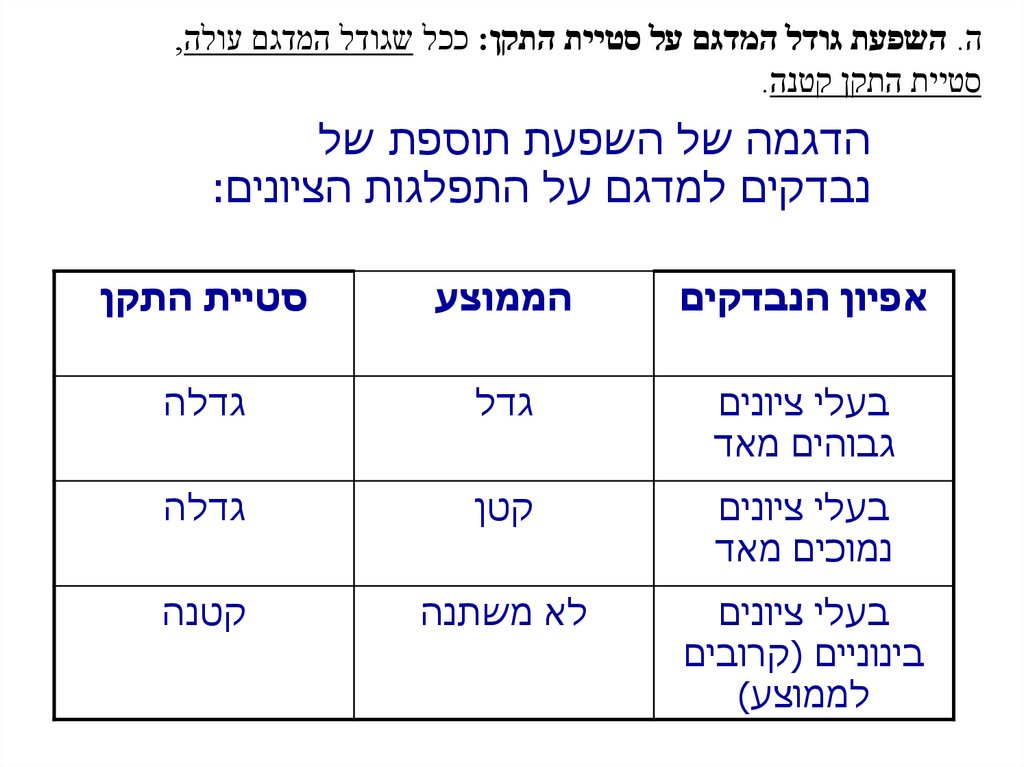
ה .השפעת גודל המדגם על סטיית התקן :ככל שגודל המדגם עולה,סטיית התקן קטנה.
הדגמה של השפעת תוספת של
נבדקים למדגם על התפלגות הציונים:
אפיון הנבדקים
הממוצע
סטיית התקן
בעלי ציונים
גבוהים מאד
גדל
גדלה
בעלי ציונים
נמוכים מאד
קטן
גדלה
בעלי ציונים
בינוניים (קרובים
לממוצע)
לא משתנה
קטנה
34.
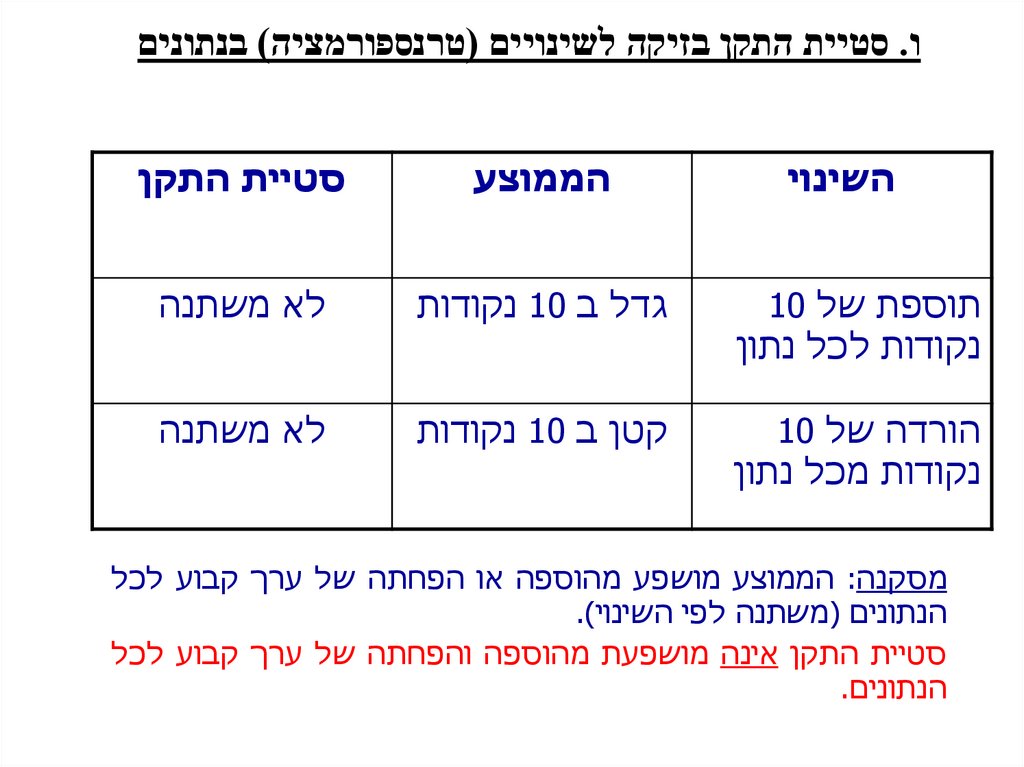
ו .סטיית התקן בזיקה לשינויים (טרנספורמציה) בנתוניםהממוצע
סטיית התקן
השינוי
תוספת של 10
נקודות לכל נתון
גדל ב 10נקודות
לא משתנה
הורדה של 10
נקודות מכל נתון
קטן ב 10נקודות
לא משתנה
מסקנה :הממוצע מושפע מהוספה או הפחתה של ערך קבוע לכל
הנתונים (משתנה לפי השינוי).
סטיית התקן אינה מושפעת מהוספה והפחתה של ערך קבוע לכל
הנתונים.
35.
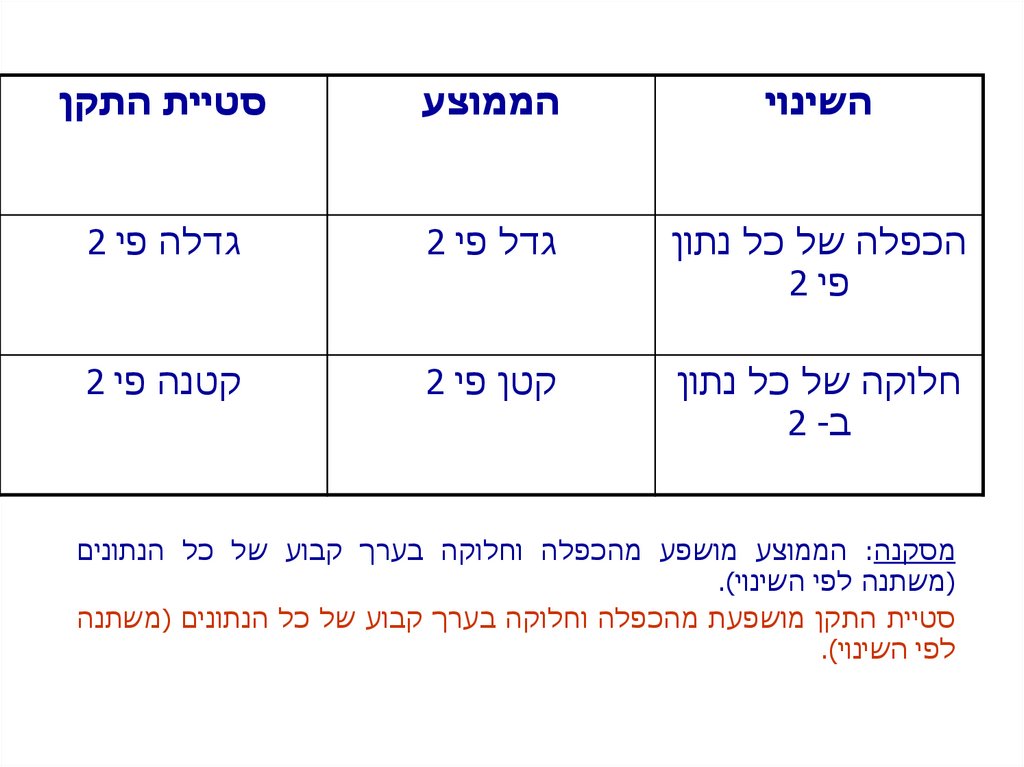
השינויהממוצע
סטיית התקן
הכפלה של כל נתון
פי 2
גדל פי 2
גדלה פי 2
חלוקה של כל נתון
ב2 -
קטן פי 2
קטנה פי 2
מסקנה :הממוצע מושפע מהכפלה וחלוקה בערך קבוע של כל הנתונים
(משתנה לפי השינוי).
סטיית התקן מושפעת מהכפלה וחלוקה בערך קבוע של כל הנתונים (משתנה
לפי השינוי).
36.
רבעוני-תחום בין/טווח) Inter-Quartile Range=IQR(
37.
•מדד זה מתאר את מידת הפיזור של האיברים במרכז ההתפלגות.
•
מבוסס על חלוקת קבוצת האיברים בהתפלגות לרבעונים:
– הרבעון הראשון ( )Q1הוא הערך ש 25%-מן האיברים בקבוצה נמוכים
ממנו
– הרבעון השני ( )Q2הוא הערך ש 50%-מן האיברים בקבוצה נמוכים
ממנו ( זה למעשה חציון!)
– הרבעון השלישי ( )Q3הוא הערך ש 75%-מן האיברים בקבוצה נמוכים
ממנו
הגדרה :טווח בין-רבעוני הוא ההפרש שבין הרבעון השלישי לרבעון הראשון:
IQR = Q3 - Q1 = upper quartile - lower quartile
= 75th percentile - 25th percentile.
עקרון אופן החישוב:
א .מחלקים את קבוצת הנתונים לשני חצאים
ב .מוצאים את החציון בכל "חצי"-זה יתן את 1Qו-
! 3Q
38.
39.
טווח בין רבעוני מייצג את 50%האמצעייםבהתפלגות ,שנמצאים משני הצדדים של
החציון:
מרכז הקבוצה מכיל את שני הרבעונים האמצעיים
בהתפלגות:
אם מחלקים סדרת איברים לשני חצאים ,על סמך
החציון ,אזי הרבעון הראשון ()1Qהוא החציון של
חלקה הראשון של ההתפלגות ,והחציון השלישי
()3Qהוא החציון של חלקה השני.
40.
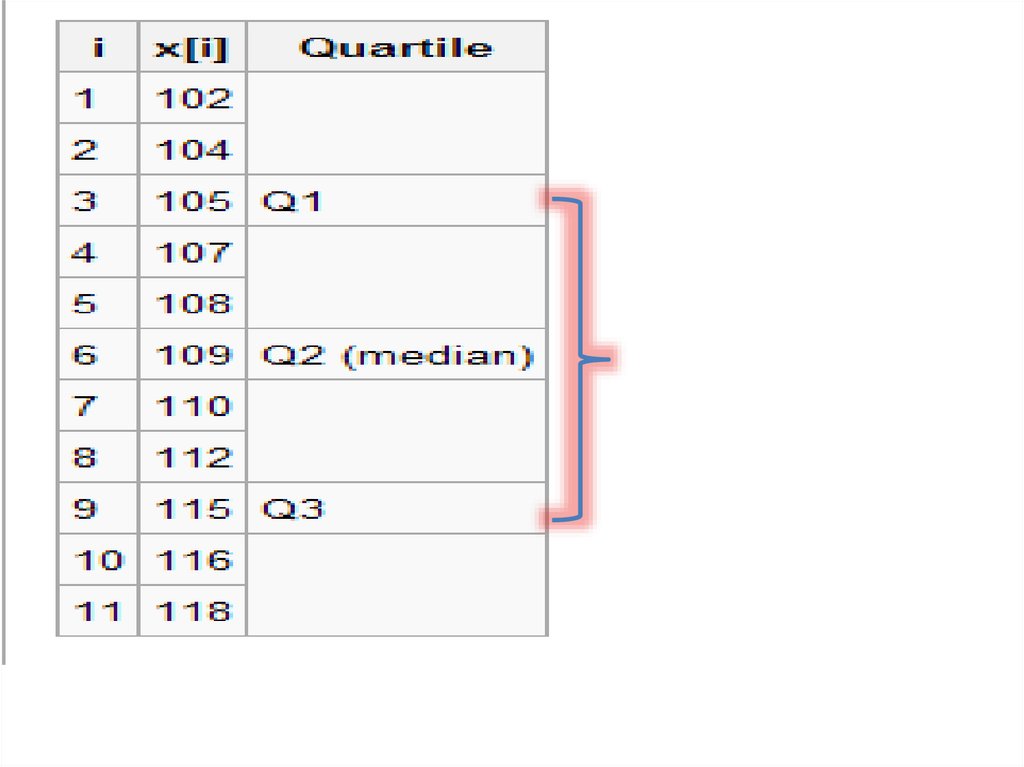
דוגמאת חישוב רבעונים-מס' אי זוגי של איברים• בקבוצה הבאה תשעה איברים:
א .נחלק את הסדרה לשני חלקים ,מסביב לחציון
ב .כעת נמצא את החציון של כל אחד מן החלקים
3, 5, 7, 8, 9, 21, 40, 90, 120
M
Q3
Q3=(40+90)/2=65
IQR=65-6=59
Q1
Q1=(5+7)/2=6
41.
חישוב IQRבאקסל:תחביר
)QUARTILE(array,quart
-Arrayטווח התאים של ערכים מספריים שעבורם מבוקש ערך הרביעון.
-Quartציון של איזה רבעון רוצים.
QUARTILEמחזירה
כאשר ערכו של quart
ערך מזערי
0
הרביעון הראשון (המאיון ה)25-
1
ערך חציון (המאיון ה)50-
2
הרביעון השלישי (המאיון ה)75-
3
ערך מרבי
4
Interquartile Range (IQR) =Q3-Q1 :
)=QUARTILE(G:G,3)-QUARTILE(G:G,1
דוגמא:
Q(0.75)=Q3:
)=QUARTILE(G:G,3
Q(0.25)=Q1:
)=QUARTILE(G:G,1
42.
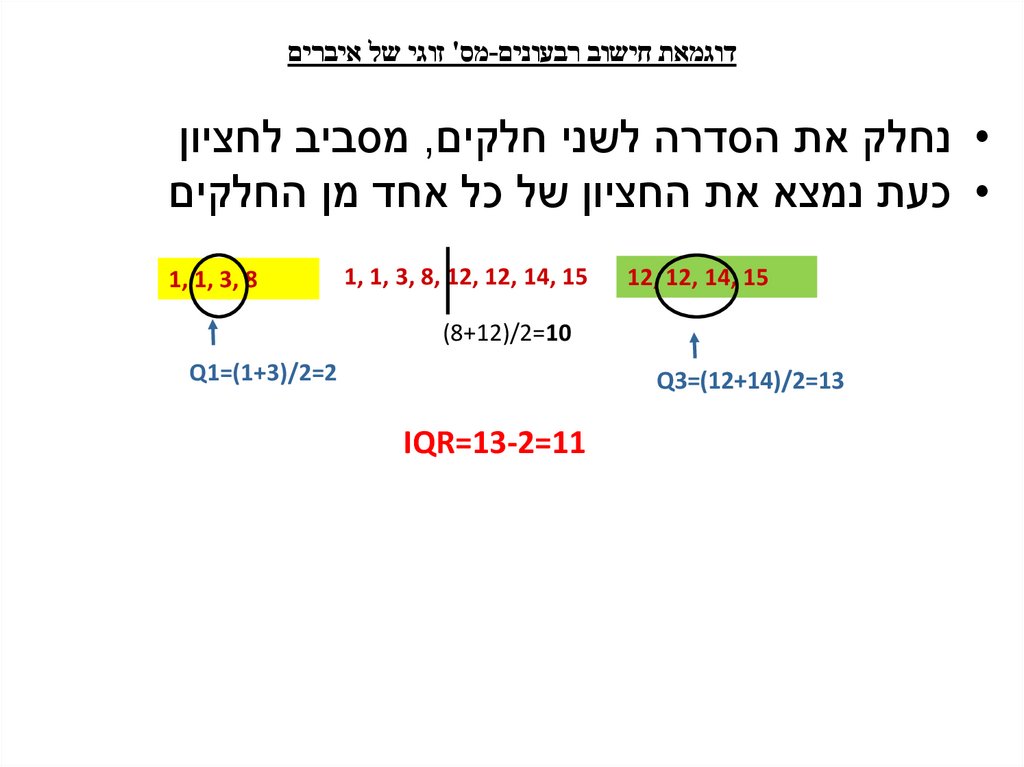
דוגמאת חישוב רבעונים-מס' זוגי של איברים• נחלק את הסדרה לשני חלקים ,מסביב לחציון
• כעת נמצא את החציון של כל אחד מן החלקים
12, 12, 14, 15
1, 1, 3, 8, 12, 12, 14, 15
1, 1, 3, 8
(8+12)/2=10
Q1=(1+3)/2=2
Q3=(12+14)/2=13
IQR=13-2=11
43.
הרחבה למתעניינים-לא תתבקשו לבצע בבחינה!חישוב רבעונים – נוסחאות כלליות
• נוסחא כללית ל n-אי-זוגי:
– הרבעון הראשון הוא האיבר הנמצא במקום ה-
– הרבעון השלישי נמצא במקום הn 3 -
( (n 1)
)
4
n 3
4
• נוסחא כללית ל n-זוגי:
– הרבעון הראשון הוא האיבר הנמצא במקום ה-
– הרבעון השלישי נמצא במקום ה-
n 2
)
4
( (n 1)
n 2
4
44.
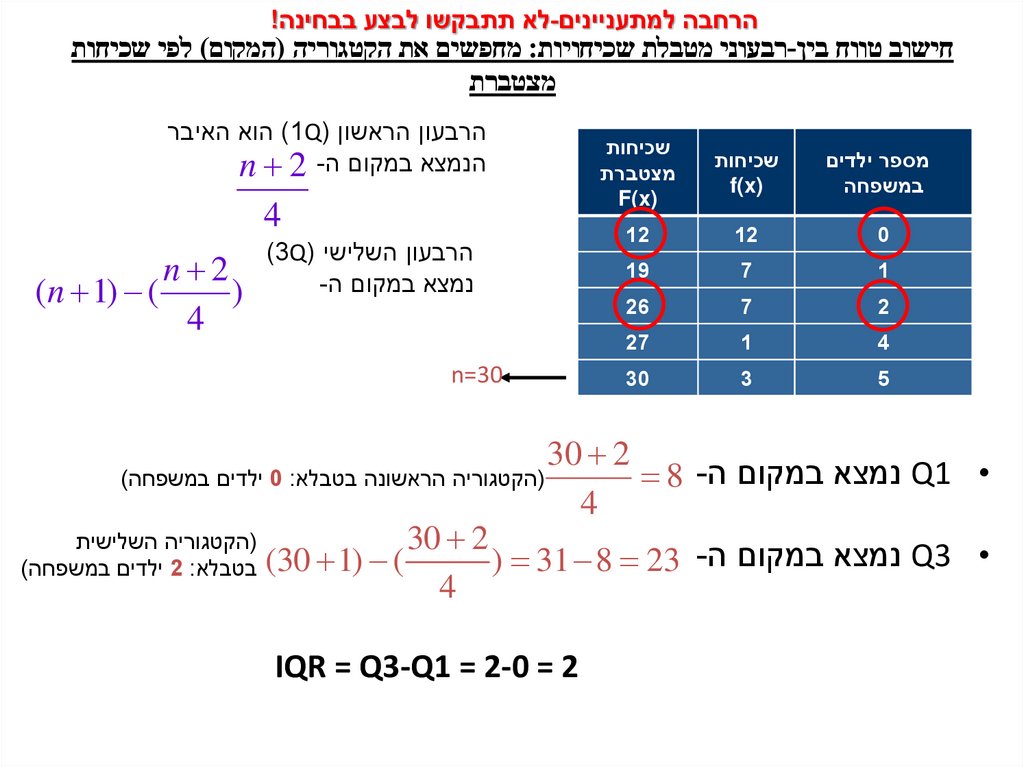
הרחבה למתעניינים-לא תתבקשו לבצע בבחינה!חישוב טווח בין-רבעוני מטבלת שכיחויות :מחפשים את הקטגוריה (המקום) לפי שכיחות
מצטברת
מספר ילדים
במשפחה
שכיחות
)f(x
שכיחות
מצטברת
)F(x
0
12
12
1
7
19
2
7
26
4
1
27
5
3
30
הרבעון הראשון ( )1Qהוא האיבר
הנמצא במקום הn 2 -
4
הרבעון השלישי ()3Q
נמצא במקום ה-
n 2
( (n 1)
)
4
n=30
30 2
(הקטגוריה הראשונה בטבלא 0 :ילדים במשפחה)
• Q1נמצא במקום ה 8 -
4
(הקטגוריה השלישית
30 2
• Q3נמצא במקום ה) 31 8 23 -
( (30 1) בטבלא 2 :ילדים במשפחה)
4
IQR = Q3-Q1 = 2-0 = 2
45.
המגבלות/חסרונות של IQR• התחום הבין-רבעוני אינו נותן את התמונה המלאה
של ההתפלגות,כי הוא מתעלם מהקצוות ומתמקד
רק במרכז ההתפלגות! (שימו לב! בניגוד ל"טווח"-
העוסק דווקא בקצוות ההתפלגות!) .לדוגמא,
בסדרה :
100 ,50 ,50 ,50 ,50 ,50 ,50 ,50 ,1
הטווח הבין-רבעוני ( )0אינו משקף את העובדה
שקצות ההתפלגות רחוקות מאוד ממרכזה!
• לא משמש להסקה סטטיסטית!
46.
שימושים של הטווח הבין-רבעוני•
•
•
•
נוח לשימוש בהתפלגויות א-סימטריות!
לא מושפע מערכים קיצוניים!
ניתן לחישוב עבור משתני רווח ומנה.
עבור משתנה בסולם סודרי -ניתן רק לציין את
הערכים שביניהם ממוקמות התצפיות שבמרכז
ההתפלגות.
• דוגמא :תוצאות לגבי משתנה רציף שנמצא בסקר
47.
דוגמאות מהספרות:48.
http://ijedict.dec.uwi.edu/images/articleimages/EDICT-2006-242-image001.gif49.
http://www.irrodl.org/index.php/irrodl/article/viewFile/674/1260/579050.
סיכום :זיקה בין מדדי הנטייה למרכזלבין מדדי הפיזור
51.
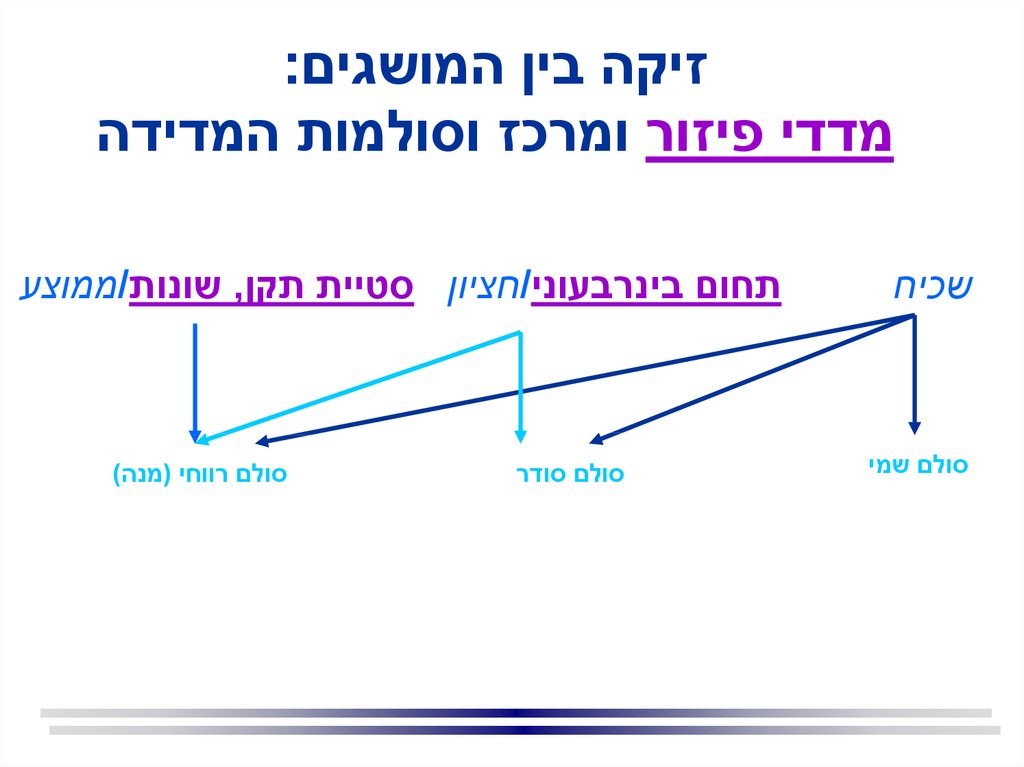
זיקה בין המושגים:מדדי פיזור ומרכז וסולמות המדידה
שכיח
סולם שמי
תחום בינרבעוני/חציון סטיית תקן ,שונות/ממוצע
סולם סודר
סולם רווחי (מנה)
52.
!לא תתבקשו לדעת בבחינה-הרחבה למתעניינים:הדגמת מאמר בחינוך
http://users.ipfw.edu/isiorho/TEACHI
NG%20GEOLOGY%20COURSES%20O
NLINE.htm



































 mathematics
mathematics





