Системы счисления

1.

Система счисления
• Система счисления - это совокупность правил
для обозначения и наименования чисел.
• Системы счисления делятся на позиционные и
непозиционные.
• Знаки, используемые при записи чисел,
называются цифрами.

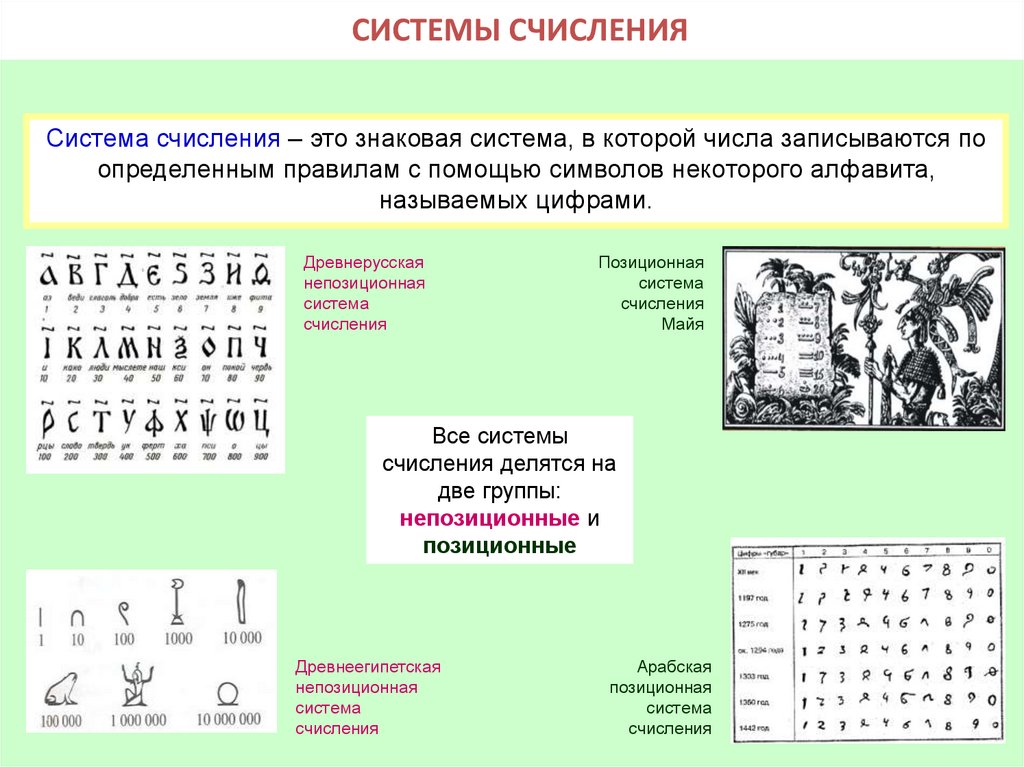
2. СИСТЕМЫ СЧИСЛЕНИЯ

Система счисления – это знаковая система, в которой числа записываются по
определенным правилам с помощью символов некоторого алфавита,
называемых цифрами.
Древнерусская
непозиционная
система
счисления
Позиционная
система
счисления
Майя
Все системы
счисления делятся на
две группы:
непозиционные и
позиционные
Древнеегипетская
непозиционная
система
счисления
Арабская
позиционная
система
счисления

3.

• Счет появился тогда, когда человеку
потребовалось информировать своих
сородичей о количестве обнаруженных
им предметов. В разных местах придумывались разные способы передачи
численной информации: от зарубок по
числу предметов до хитроумных знаков цифр. Во многих местах люди стали
использовать для счета пальцы. Одна из
таких систем счета и стала общеупотребительной – десятичная

4. продолжение

До сих пор существуют в Полинезии племена с 20-чной системой счисления (с учетом пальцев
на ногах).
Сегодня мы настолько сроднились с 10-чной системой счисления, что не представляем себе
иных способов счета, пока не вспомним о времени. Нас не смущает, что в минуте 60 секунд, а
не 10 или 100. И в часе 60 минут, но более удивительно, что в сутках 24 часа, а в году 365 дней.
Таким образом, время (часы и минуты) мы считаем в 60-чной системе, сутки - в 24-чной,
недели в 7-чной,месяцы совсем хитро - каждый по своему, года в 12-чной, если в месяцах, или
в 365-чной, если в днях. Другими словами, все дело в привычке. Конечно, когда идет дождь,
можно раскрыть зонтик и не думать, почему он пошел, но разобраться в причинах тоже
полезно. Сейчас мы постараемся понять принцип счета. Только давай сразу договоримся, что
мы будем обсуждать не все способы счета (системы счисления), а ограничимся только
позиционными. Два примера непозиционных систем счисления я приведу после определения
позиционных систем.

5. Как изображали числа?

• Числа
изображали
засечками
на
деревянных дощечках клиньями на
глиняных табличках; узелками на веревках;
иероглифами; буквами; цифрами.

6. Непозиционные системы счисления

Непозиционной называется такая система
счисления, у которой количественный
эквивалент («вес») цифры не зависит от ее
местоположения записи числа.
• Единичная система счисления
• Древнеегипетская
• Римская
• Греческая
• Алфавитная

7. ЕДИНИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ

Находки археологов на стоянках
первобытных людей свидетельствуют о
том, что первоначально количество
предметов отображали равным
количеством каких-либо значков (бирок):
зарубок, черточек, точек.
Позже значки стали группировать по три
или по пять.
Такая система записи чисел называется
единичной (унарной), так как любое число в
ней образуется путем повторения одного
знака, символизирующего единицу.
Отголоски единичной системы счисления
встречаются и сегодня (счетные палочки
для обучения счету; полоски, нашитые на
рукаве, означают на каком курсе учится
курсант военного училища).
Отображение количества предметов узелками

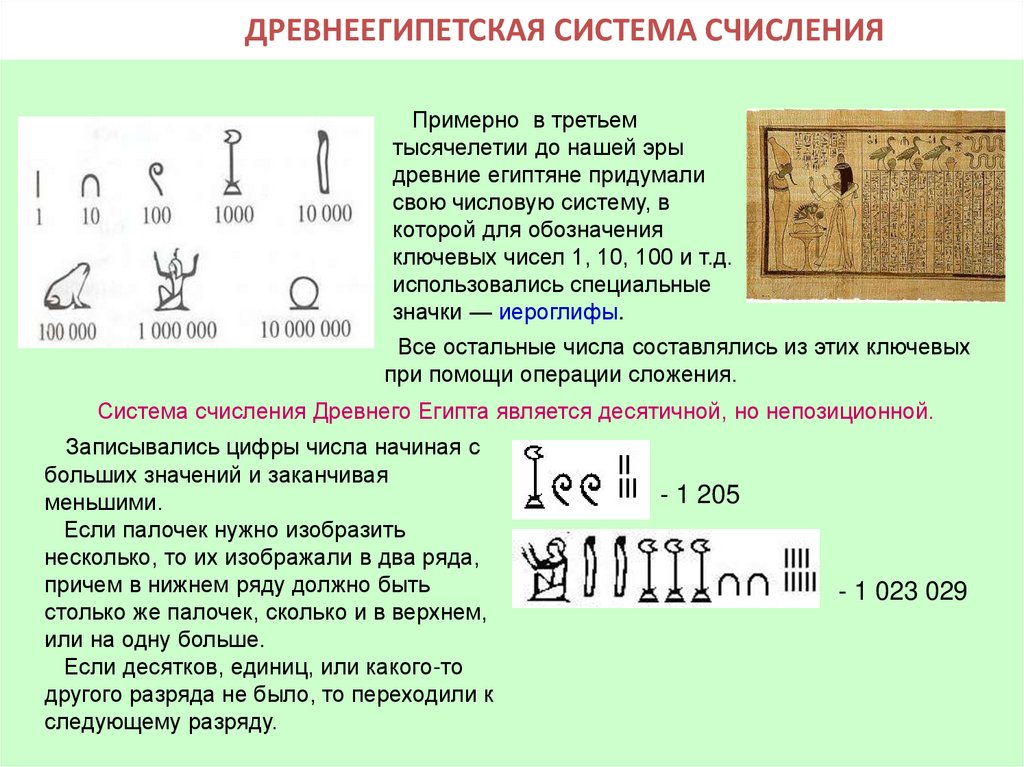
8. ДРЕВНЕЕГИПЕТСКАЯ СИСТЕМА СЧИСЛЕНИЯ

Примерно в третьем
тысячелетии до нашей эры
древние египтяне придумали
свою числовую систему, в
которой для обозначения
ключевых чисел 1, 10, 100 и т.д.
использовались специальные
значки — иероглифы.
Все остальные числа составлялись из этих ключевых
при помощи операции сложения.
Система счисления Древнего Египта является десятичной, но непозиционной.
Записывались цифры числа начиная с
больших значений и заканчивая
меньшими.
Если палочек нужно изобразить
несколько, то их изображали в два ряда,
причем в нижнем ряду должно быть
столько же палочек, сколько и в верхнем,
или на одну больше.
Если десятков, единиц, или какого-то
другого разряда не было, то переходили к
следующему разряду.
- 1 205
- 1 023 029

9. РИМСКАЯ СИСТЕМА СЧИСЛЕНИЯ

В основе римской
системы счисления
лежали знаки I (один
палец) для числа 1,
V (раскрытая
ладонь) для числа 5,
Х (две сложенные
ладони) для 10.
Календарь на каменной плите, найденный в Риме
Для обозначения чисел 100, 500 и 1000
применяются первые буквы соответствующих
латинских слов (Centum - сто, Demimille половина тысячи, Mille - тысяча).
Число обозначается набором стоящих подряд цифр.
Значение числа определяется как сумма или разность цифр в числе.
Если меньшая цифра стоит слева от большей, то она вычитается, если справа, то
прибавляется.
Например, число 1794 будет записано так: MDCCXCIV.

10. ГРЕЧЕСКАЯ АЛФАВИТНАЯ СИСТЕМА СЧИСЛЕНИЯ

В алфавитной системе
счисления Древней Греции числа
1, 2, …, 9 обозначались первыми
девятью буквами греческого
алфавита (α, β, γ, …).
Для обозначения чисел 10, 20, …, 90
применялись следующие 9 букв (ι, κ, λ,…).
Для обозначения чисел 100, 200, …, 900 –
последние 9 букв (ρ, σ, τ,…).
Чтобы не путать числа с буквами, над ними
ставили черточку.
Например, число 141 обозначалось ρμα.
Для обозначения тысяч греки использовали те
же буквы, но при их записи слева внизу ставили
косую черточку.
Число 10 000 греки называли мириадой.
Таким способом греки могли записать числа до
108. Это число называлось мириада мириад.
Это самое больше число которое называли и
записывали греки.

11. СЛАВЯНСКАЯ АЛФАВИТНАЯ СИСТЕМА СЧИСЛЕНИЯ

У славянских народов
числовые значения букв
установились в порядке
славянского алфавита,
который использовал
сначала глаголицу, а затем
кириллицу.
Древнерусская алфавитная система счисления,
использующая кириллицу
Над буквами, обозначающими числа,
ставился специальный знак «~» - титло.
Самая высшая из величин называлась
«колода» (1050). Считалось, что «боле сего
несть человеческому уму разумевати».
В России славянская нумерация
сохранилась до конца XVII века. При Петре I
возобладала так называемая арабская
нумерация, которой мы пользуемся и сейчас.
Славянская нумерация сохранилась только
в богослужебных книгах.

12. НЕДОСТАТКИ НЕПОЗИЦИОННЫХ СИСТЕМ СЧИСЛЕНИЯ

1. Существует постоянная
потребность введения новых
знаков для записи больших чисел
2. Невозможно представлять
дробные и отрицательные числа.
3. Сложно выполнять
арифметические операции, так как
не существует алгоритмов их
выполнения.

13.

В позиционных системах счисления величина, обозначаемая цифрой в записи числа,
зависит от ее позиции.
Количество используемых цифр называется основанием позиционной системы счисления.
Система счисления, применяемая в современной математике, является позиционной десятичной системой.
Основание ее равно 10, т.е. запись любых чисел производится с помощью десяти цифр 0 1 2 3 4 5 6 7 8 9.
Пример:
333
сотни десятки единицы
Для записи чисел в позиционной системе счисления с основанием p нужно
иметь алфавит из р цифр. Обычно для этого при р<10 используют р первых
арабских цифр, при р>10 к десяти арабским цифрам добавляют латинские буквы.
Примеры алфавитов нескольких систем
основание название алфавит
р=2 двоичная 0 1
р=3 троичная 0 1 2
р=8 восьмеричная 0 1 2 3 4 5 6 7
р=16 шестнадцатеричная 0 1 2 3 4 5 6 7 8 9 A B C D E F
Достоинства позиционных систем счисления
Простота выполнения арифметических операций.
Ограниченное количество символов (цифр) для записи любых чисел

14. КОМПЬЮТЕРНЫЙ ПРАКТИКУМ

Римская система счисления

15. Таблица позиционной системы

Название
Цифры
Основание
Двоичная
0,1
2
Восьмеричная
0,1,2,3,4,5,6,7
8
Десятичная
0,1,2,3,4,5,6,7,8,9
10
Шестнадцатеричная
0,1,2,3,4,5,6,7,8,9,
A(10),B(11),C(12),
D(13),E(14),F(15)
16

16. Развернутая форма записи числа

• А = ± (а + , а +.. . + а +а 2q2+.. . ) развернутая форма записи числа.
• Здесь:
• А-само число,
• q - основание системы счисления, а - цифры данной системы
счисления (а; an { и др.), n - число разрядов целой части числа,
• m - число разрядов дробной части числа.
• Пример
• Записать в развернутом виде число А10= 4718,63
• А10 = 4*103+7* 10 2 +1 * 10+8*10°+6*10 +З*10-2

17. Задания

• 1. Какие числа записаны с помощью римских цифр:
MMIV,LXV,CMLXIIV
• 2. Переведите числа в римскую систему счисления:
132, 2008, 356, 32
• 3.Запишите число в развернутом виде:
2638; 345,178; 112; 368
• 4. Запишите числа в свернутом виде:
А(16) = А*16(1)+1*16(0)+7*16(-1)+5*16(-2)=
А(10) = 9*10(1)+1*10(0)+5*10(-1)+3*10(-2)=