Similar presentations:
Les équations différentielles relatives aux oscillateurs mecaniques le pendule simple
1. Diapositive 1
LES ÉQUATIONS DIFFÉRENTIELLES RELATIVES AUX OSCILLATEURSMECANIQUES
LE PENDULE SIMPLE
2. Diapositive 2
QUELQUES REMARQUES PRELIMINAIRESUn mouvement harmonique simple existe lorsqu’une force de rappel est appliquée
au système.
Cette force est proportionnelle et de sens opposé au déplacement repéré
par rapport à une position d’équilibre
Dans un mouvement harmonique simple, l’énergie cinétique et l’énergie potentielle
changent constamment.
Leur somme, l’énergie mécanique, demeure constante
Lors d’oscillations simples, l’amplitude est constante et la période est
indépendante de l’amplitude
3. Diapositive 3
Il peut se produire un phénomène de résonance dans le cas où le systèmeest entraîné par une force périodique dont la fréquence est proche de la fréquence
propre d’oscillation du système
Les systèmes soumis à des forces élastique (proportionnelles à la déformation)
décrivent un mouvement sinusoïdal Ils constituent des oscillateurs harmoniques
Dans le cas d’oscillations mécaniques
le système subit un déplacement linéaire ou angulaire
Oscillations non mécaniques
(phénomènes électriques)
Oscillations harmoniques simples
(oscillations sans perte d’énergie)
Oscillations harmoniques amorties
(existence de frottements, diminution de l’énergie)
4. Diapositive 4
TERMINOLOGIEMouvement périodique
Mouvement ou évènement qui se répète à des intervalles réguliers
x (t ) x (t T )
T
période du mouvement
unité : seconde (s)
1
f
T
f
fréquence
unité : s-1 ou hertz (HZ)
1 Hz = 1 oscillation par seconde
Oscillations
mouvement de va et vient entre deux positions extrêmes sur une trajectoire donnée
autour d’une position d’équilibre stable (d’une valeur d’équilibre ou valeur centrale)
5. Diapositive 5
DEFINITIONon appelle pendule tout système pouvant osciller dans un plan vertical
autour d’un point fixe
un pendule simple est constitué d’un objet ponctuel suspendu à un point fixe
par un fil de longueur l invariable et de masse négligeable
O
position d’équilibre
stable
Système : bille de masse m
Référentiel : géocentrique
Supposé galiléen
Repère : attaché à la bille
Forces extérieures appliquées
à la bille :
T
T
l
T
m
P mg
P
tension du fil
poids
Principe d’inertie
appl
F
ext P R 0
6. Diapositive 6
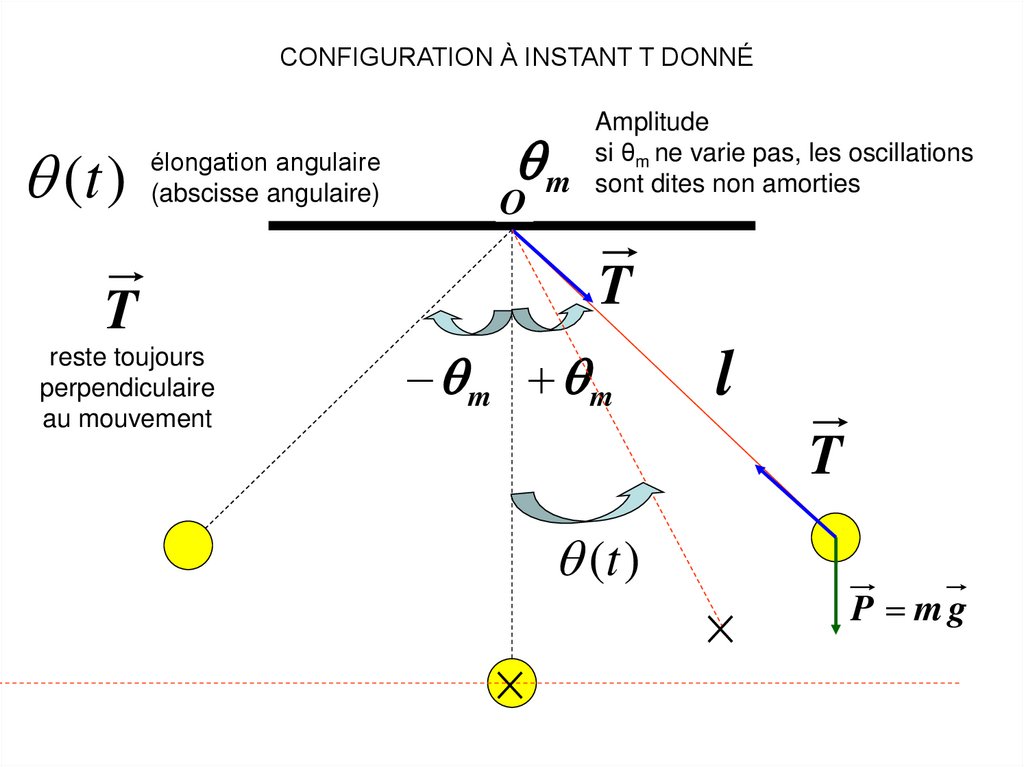
CONFIGURATION À INSTANT T DONNÉ(t )
élongation angulaire
(abscisse angulaire)
T
reste toujours
perpendiculaire
au mouvement
m
O
Amplitude
si θm ne varie pas, les oscillations
sont dites non amorties
T
m m
l
T
(t )
P mg
7. Diapositive 7
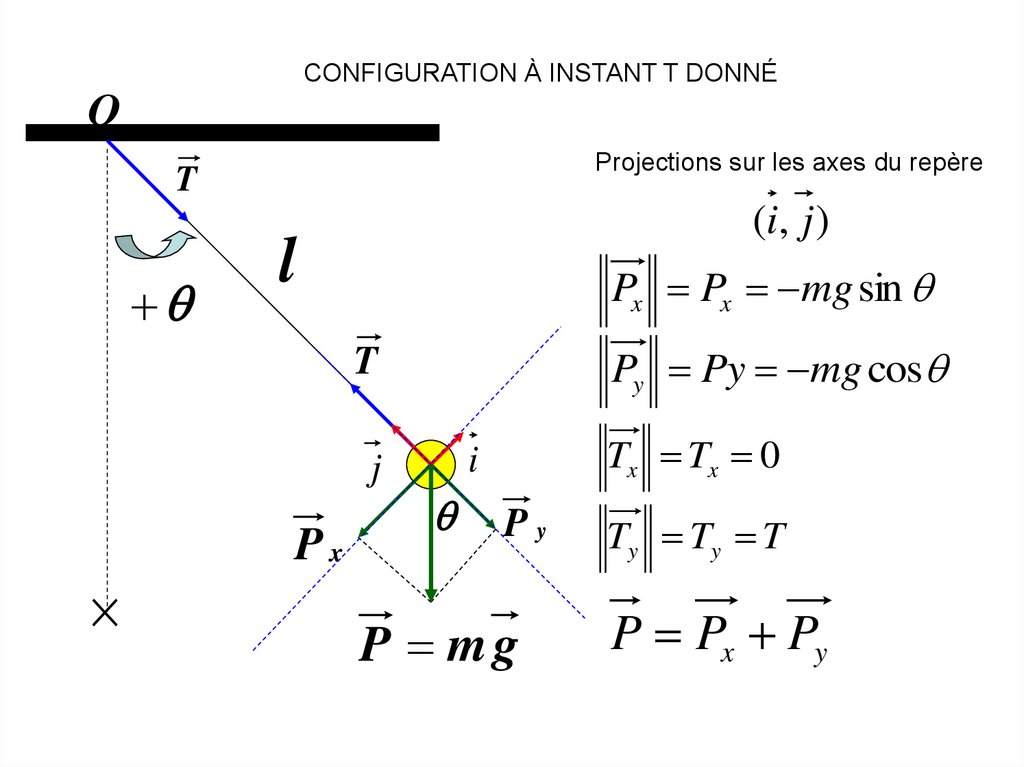
CONFIGURATION À INSTANT T DONNÉO
Projections sur les axes du repère
T
(i, j )
l
Px Px mg sin
Py Py mg cos
T
j
Px
Tx Tx 0
i
Py
P mg
Ty Ty T
P Px Py
8. Diapositive 8
POSITION D’ÉQUILIBRE STATIQUE À UN INSTANT DONNÉP T 0
projection sur les deux axes perpendiculaires
i
j
Oy, axe radial
Ox, tangente au mouvement
Py mg cos
Px mg sin
Ty mg cos 0
Tx 0
Ty mg cos
F
appl
ext
P T ( Px Py ) (Tx Ty ) Px
Px Force de rappel vers la position d’équilibre
9. Diapositive 9
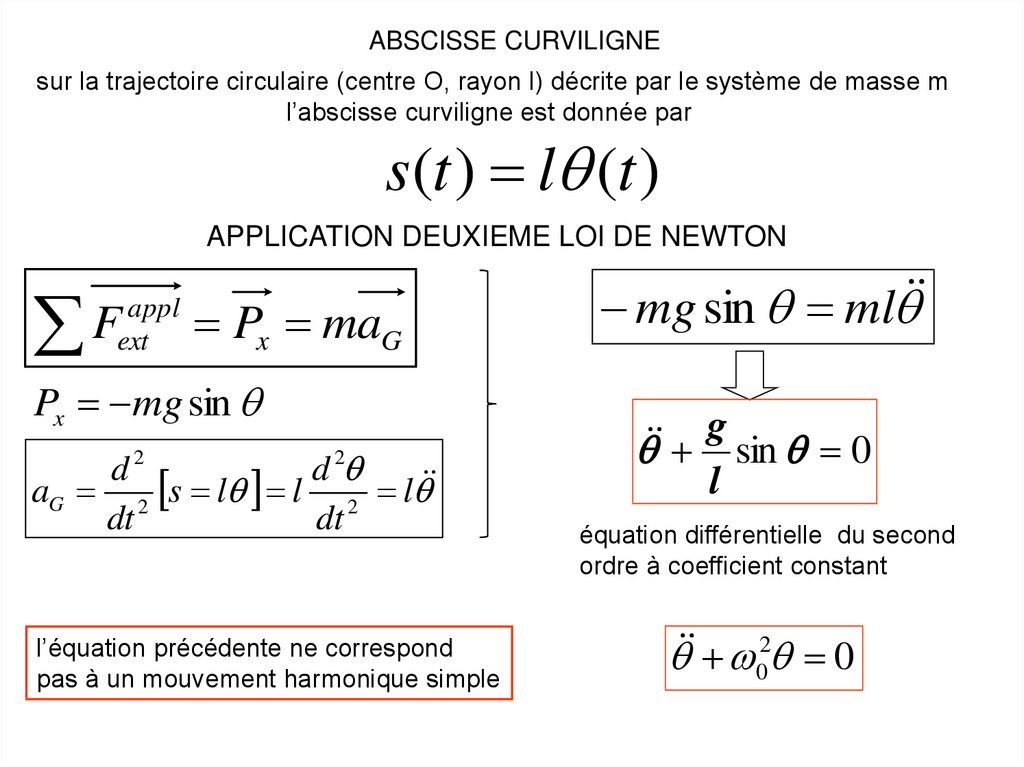
ABSCISSE CURVILIGNEsur la trajectoire circulaire (centre O, rayon l) décrite par le système de masse m
l’abscisse curviligne est donnée par
s(t ) l (t )
APPLICATION DEUXIEME LOI DE NEWTON
F
appl
ext
Px maG
Px mg sin
d2
d 2
aG 2 s l l 2 l
dt
dt
l’équation précédente ne correspond
pas à un mouvement harmonique simple
mg sin ml
g
sin 0
l
équation différentielle du second
ordre à coefficient constant
02 0
10. Diapositive 10
HYPOTHESE DES PETITES OSCILLATIONSISOCHRONISME
en radians
petit sin
équation du mouvement dans ces conditions
g
sin 0
l
g
0
l
02 0
on retrouve l’écriture générale du mouvement harmonique simple
g
l
2
0
g
0
l
M cos( 0t 0 )
g
T 2
l
Si l'angle θ devient trop grand, la vitesse de la boule est très grande au passage à l'équilibre
et les frottements fluides dus à l'air ne sont plus négligeables. La période varie au cours du
temps.
11. Diapositive 11
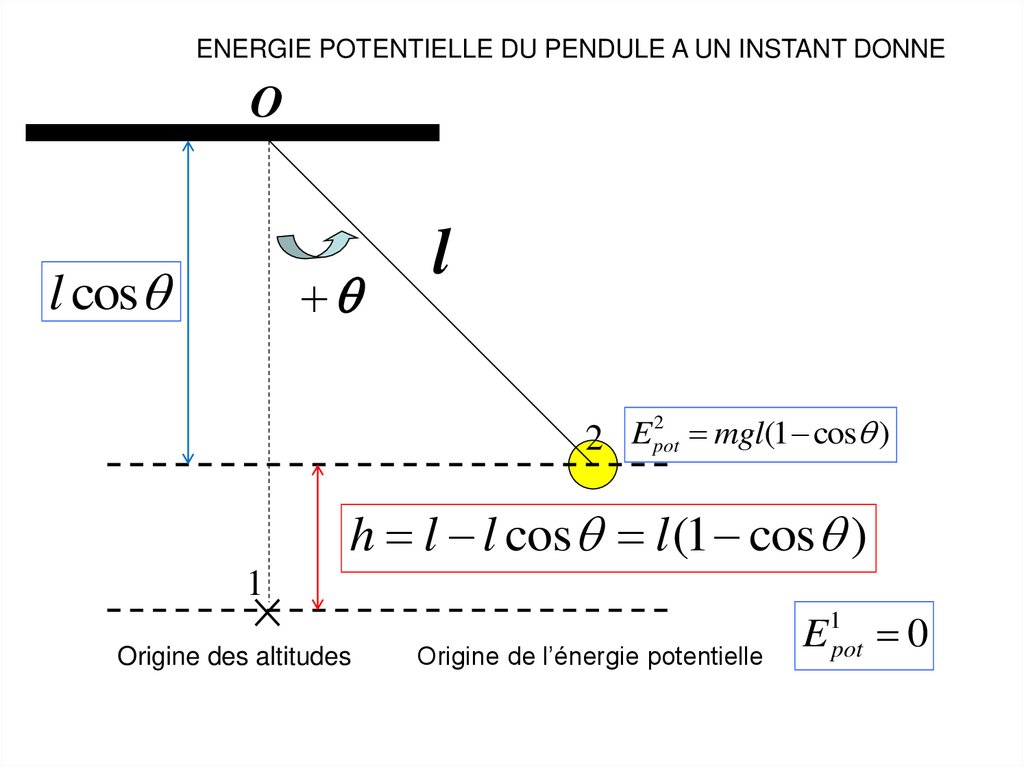
ENERGIE POTENTIELLE DU PENDULE A UN INSTANT DONNEO
l cos
l
2
E
2 pot mgl(1 cos )
h l l cos l (1 cos )
1
Origine des altitudes
Origine de l’énergie potentielle
E1pot 0
12. Diapositive 12
ENERGIE CINETIQUE DU PENDULE A UN INSTANT DONNERappel de l’abscisse curviligne :
s(t ) l (t )
VITESSE
ds d
d
v
[l ] l l
dt dt
dt
Ecin
1 2 1
2
mv m(l )
2
2
13. Diapositive 13
ENERGIE MECANIQUE DU PENDULE A UN INSTANT DONNEEmécanique Ecinétique E potentielle
E mécanique
1 2 2
ml mgl (1 cos )
2
REMARQUES
Le système est isolé, pas de frottements, il y a conservation de l’énergie mécanique
dans le cas d’un oscillateur non amorti (pendule simple)
le travail de la tension est nul : la force est perpendiculaire au déplacement
14. Diapositive 14
VARIATION DE L’ÉNERGIE MÉCANIQUE EN FONCTION DU TEMPSL’énergie mécanique est constante donc :
d
[ Eméc ] 0
dt
d 1
[ ml 2 2 mgl (1 cos )] 0
dt 2
ml 2 mgl sin 0
g
sin 0
l
On aboutit à l’équation
différentielle obtenue en
utilisant les lois de Newton
15. Diapositive 15
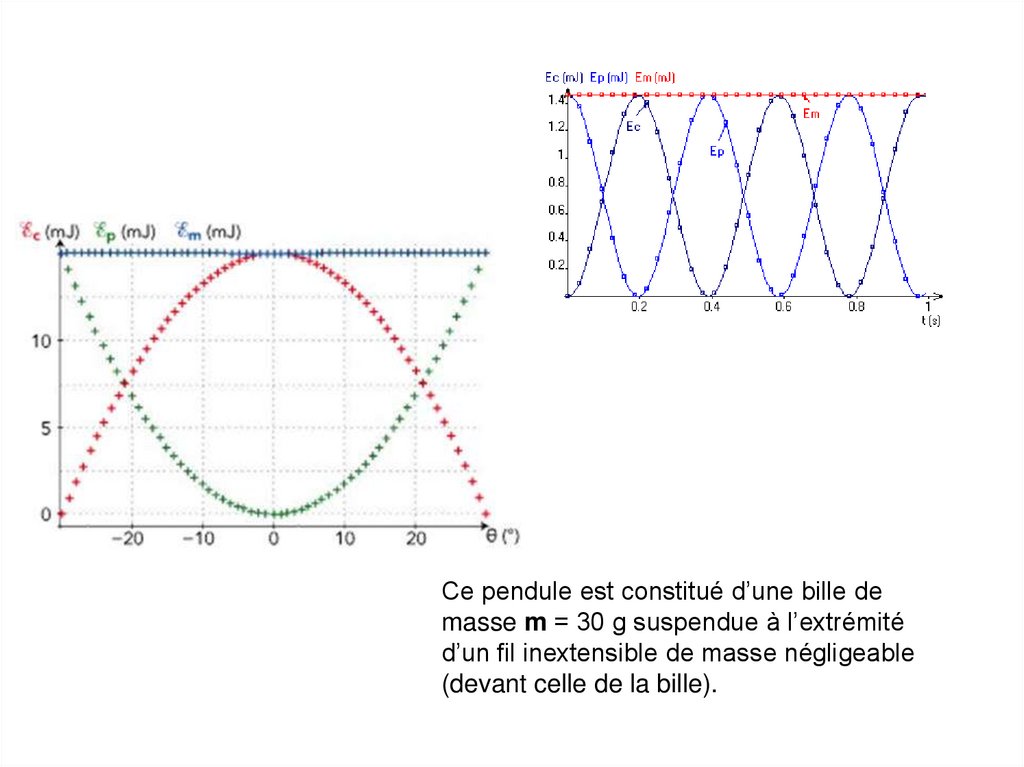
Ce pendule est constitué d’une bille demasse m = 30 g suspendue à l’extrémité
d’un fil inextensible de masse négligeable
(devant celle de la bille).
16. Diapositive 16
E2E mécanique
2mgl
énergie potentielle
maximum
E1
0
O
0
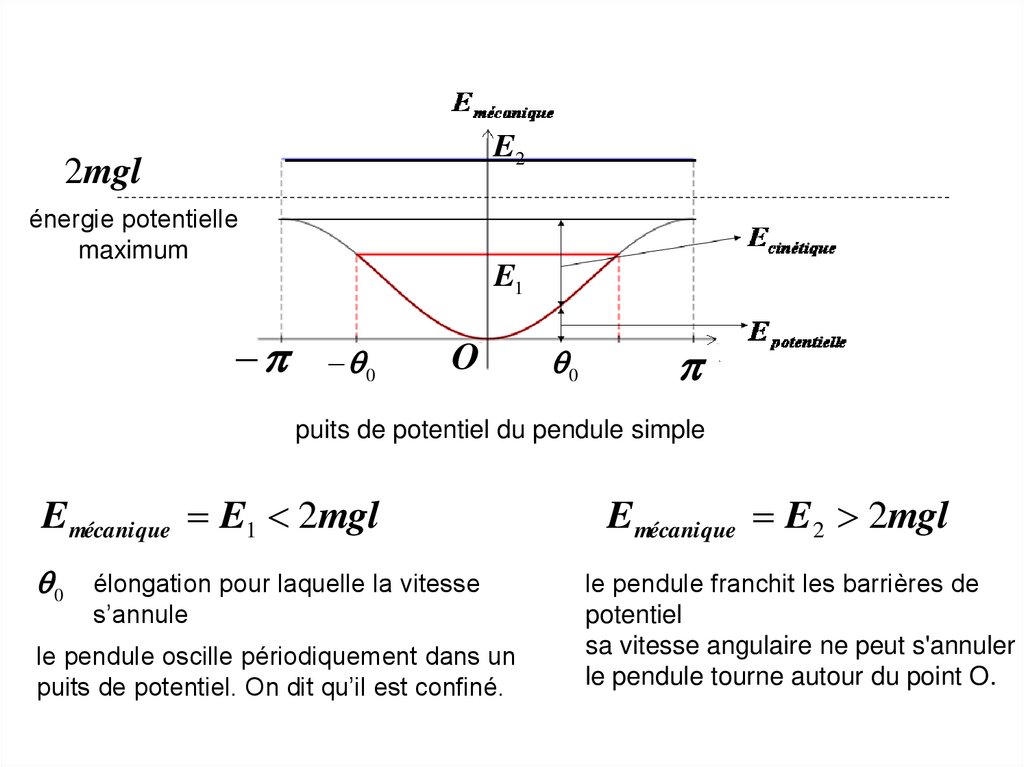
puits de potentiel du pendule simple
Emécanique E1 2mgl
0
élongation pour laquelle la vitesse
s’annule
le pendule oscille périodiquement dans un
puits de potentiel. On dit qu’il est confiné.
Emécanique E2 2mgl
le pendule franchit les barrières de
potentiel
sa vitesse angulaire ne peut s'annuler
le pendule tourne autour du point O.
17. Diapositive 17
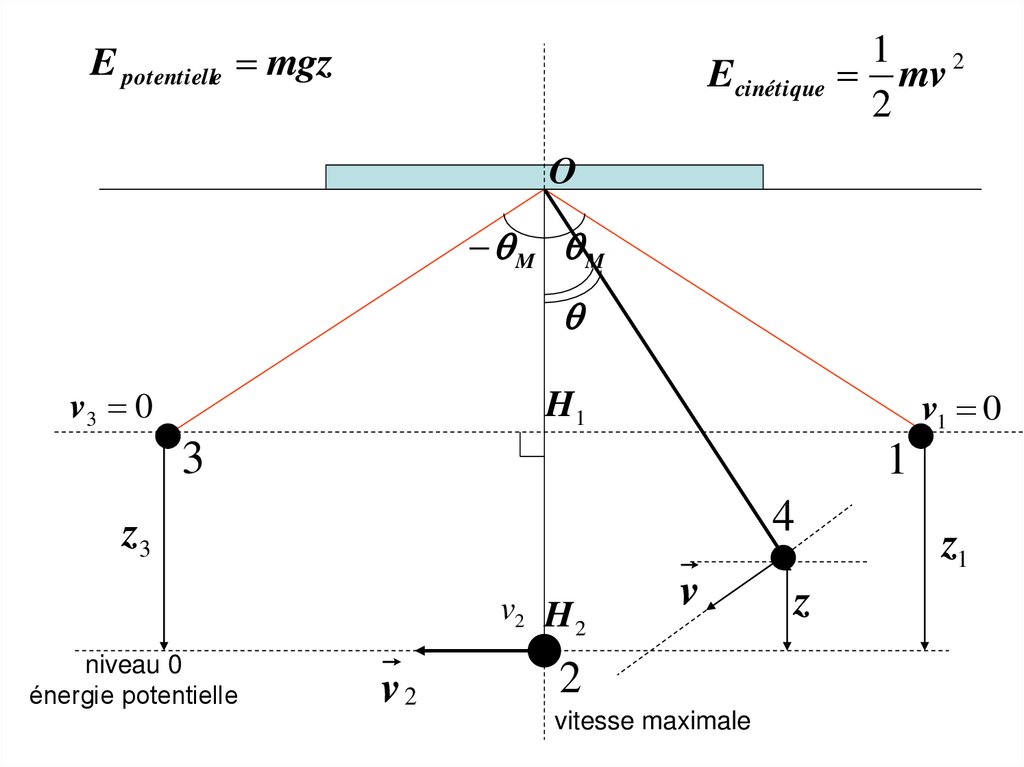
E potentielle mgzEcinétique
1
mv 2
2
O
M M
v3 0
v1 0
H1
3
1
4
z3
v2 H
2
niveau 0
énergie potentielle
v2
v
2
vitesse maximale
z1
z
18. Diapositive 18
POSITIONENERGIE
CINETIQUE
ENERGIE
POTENTIELLE
ENERGIE
MECANIQUE
1
0
mgz1
mgz1
2
1
mv 22
2
0
1
mv 22
2
3
0
mgz 3
mgz 3
4
1
mv 2
2
mgz
1 2
mv mgz
2
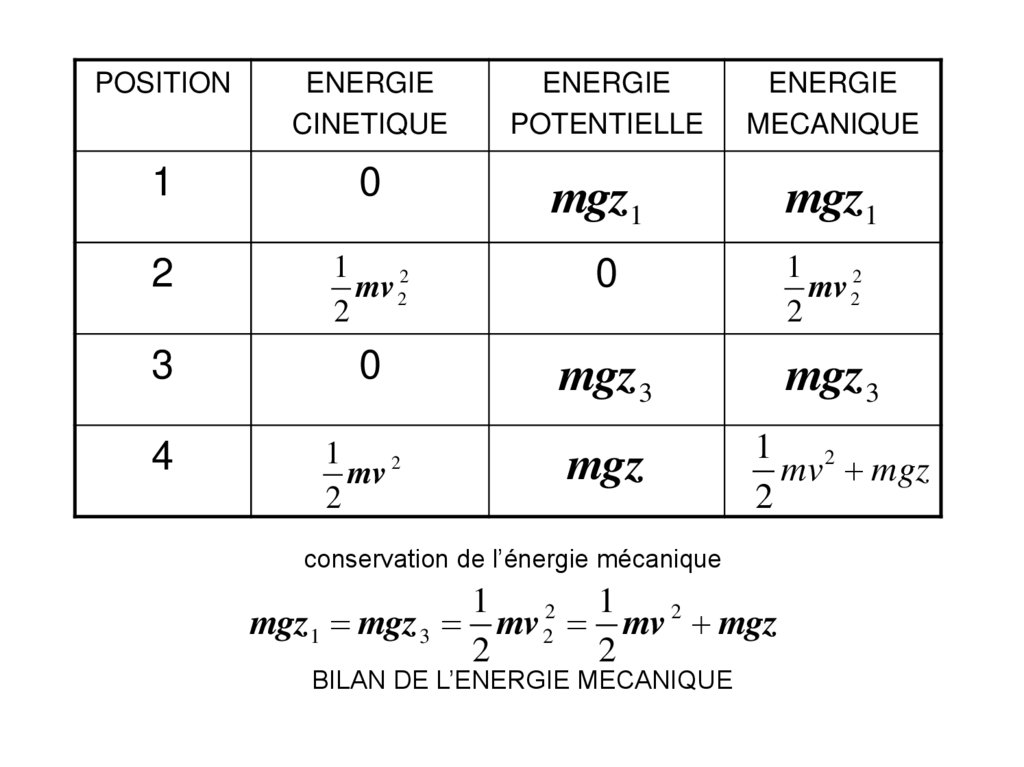
conservation de l’énergie mécanique
1
1
2
mgz1 mgz 3 mv 2 mv 2 mgz
2
2
BILAN DE L’ENERGIE MECANIQUE
19. Diapositive 19
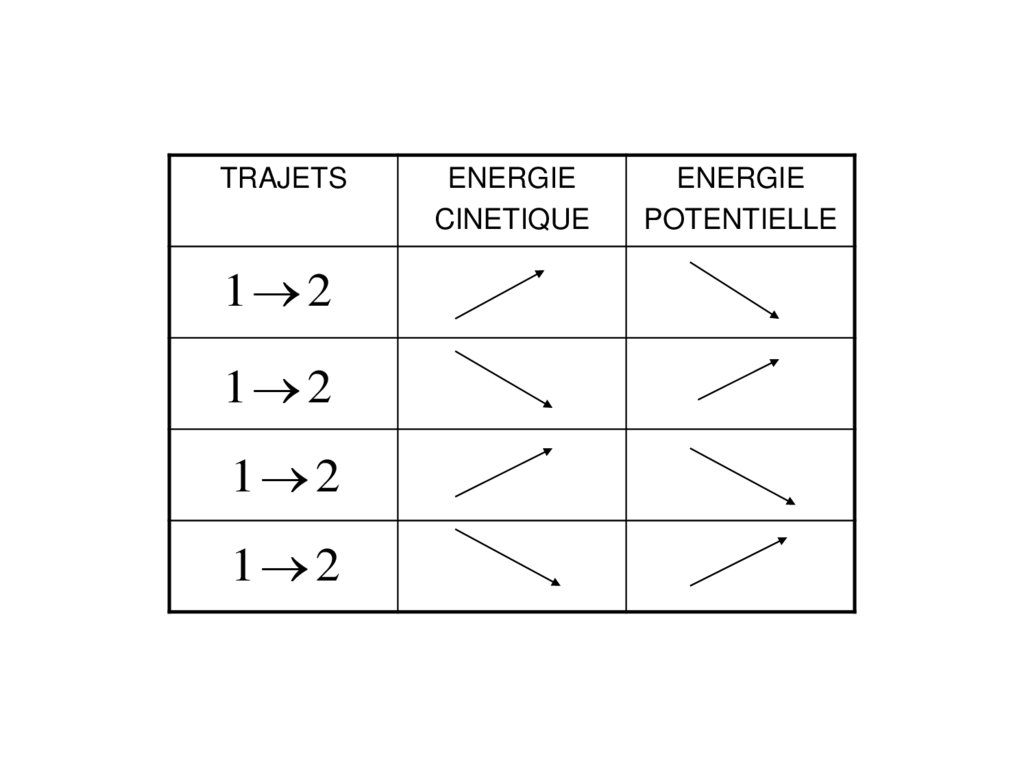
TRAJETS1 2
1 2
1 2
1 2
ENERGIE
CINETIQUE
ENERGIE
POTENTIELLE










 physics
physics
