Элементы математической статистики. (Лекция 6)

1. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

2. СТАТИСТИКА ЗНАЕТ ВСЕ

О
СТАТИСТИКА
СТАТИСТИКЕ
ЗНАЕТ
СЛЫШАЛИ
ВСЕ
ВСЕ

3. Статистика, возможно, знает все. Но ее знают не все.

Статистика,
возможно, знает все.
Александр
Но ее знают не все.
Самойленко

4. А. Тьер (1797-1877)

Статистика искусство
давать точные
данные о том,
чего не знаешь
Тьер - главный
душитель Коммуны

5. Б. Дизраэли (1804-1881)

Имеются три
рода лжи:
ложь,
наглая ложь
и
статистика.

6. Б. Дизраэли (1804-1881)

В жизни, как
правило,
преуспевает
больше тот, кто
располагает
лучшей
информацией.

7.

Не считаясь с
выводами
статистики, вы
уподобляетесь
страусу, который
зарывает голову
в песок при виде
опасности.
А. Вагнер (1835-1917)

8. ВЫБОРОЧНЫЙ МЕТОД

1.
2.
3.
Генеральная и выборочная
совокупности.
Статистическое распределение
выборки.
Основные выборочные и
генеральные характеристики.

9. 1. Генеральная и выборочная совокупности

10. Генеральная совокупность -

Генеральная совокупность множество всех объектов,
подлежащих изучению.
ГС

11. Выборочная совокупность (выборка) -

Выборочная совокупность
(выборка) множество случайно отобранных
из генеральной совокупности
объектов .
ВС

12. ЗАДАЧА выборочного метода:

на основании изучения свойств выборки
сделать какие-либо утверждения о
свойствах всех элементов генеральной
совокупности.

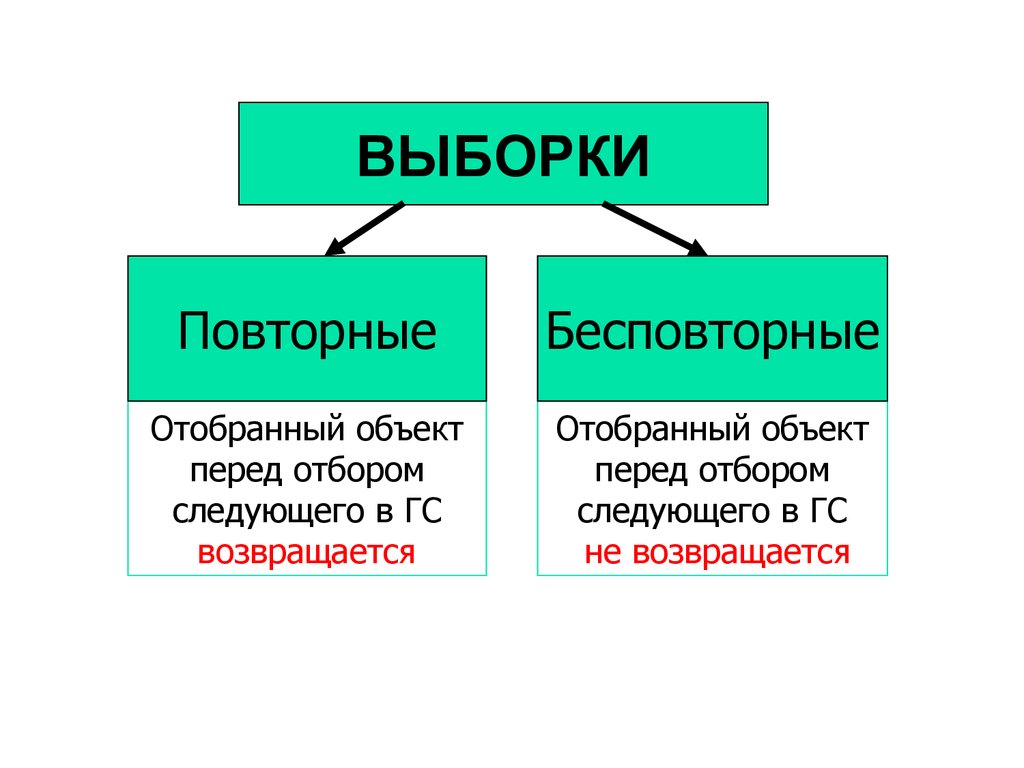
13.

ВЫБОРКИ
Повторные
Бесповторные
Отобранный объект
перед отбором
следующего в ГС
возвращается
Отобранный объект
перед отбором
следующего в ГС
не возвращается

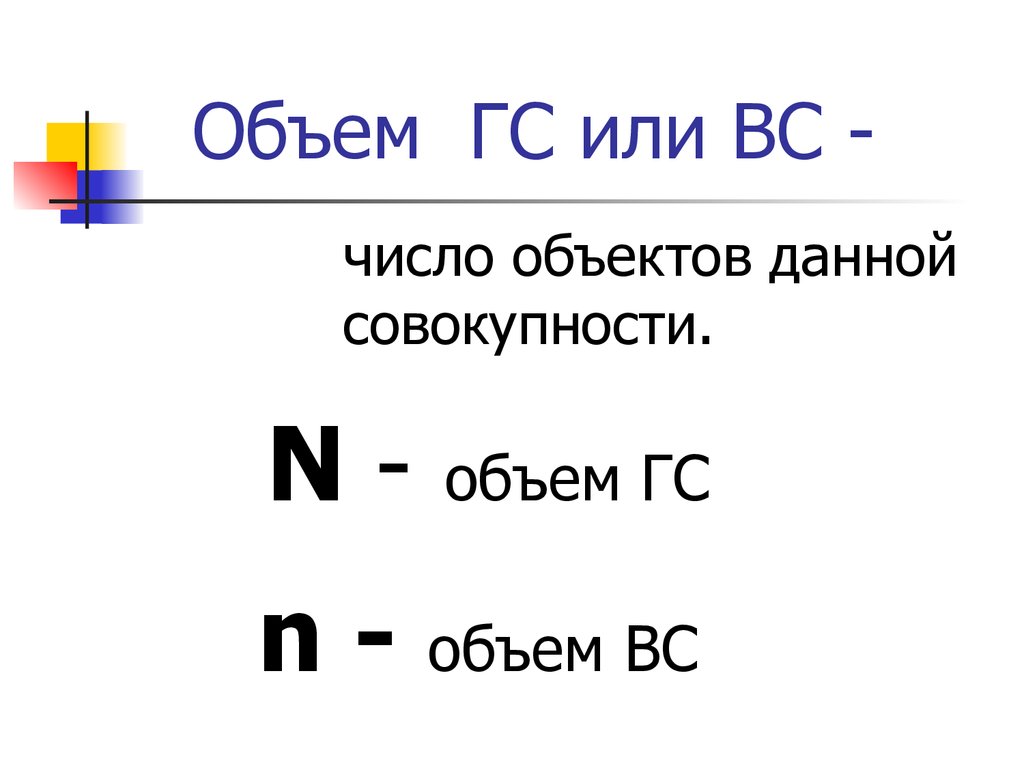
14. Объем ГС или ВС -

Объем ГС или ВС число объектов данной
совокупности.
N-
объем ГС
n - объем ВС

15. Относительный показатель ВС -

Относительный
показатель ВС отношение объема ВС к
объему ГС
n
k
N

16. СВОЙСТВА ВЫБОРКИ:

1. достаточно объемна;
2. репрезентативна (представительна).

17.

1936 г.
Журнал
«Литературное
обозрение»
Социологи
Дж. Геллап
Э. Роупер
4 000 000
4 000
н
а
Л
з
у
Р
н
о
д
е
в
т
ь
л

18.

Франклин Делано Рузвельт

19. 2. Статистическое распределение выборки.

20.

x1 - n1
x 2 – n2
…
xk – nk
n1 n2 ... nk n

21. Варианты -

наблюдаемые значения признака: x1,
x2, ... , xк

22. Вариационный ряд -

Вариационный ряд последовательность вариант,
расположенных в порядке
возрастания.

23. Пример:

При измерении диаметра 11 дробин получены
следующие данные:
4,55, 4,59, 4,65, 4,59, 4,75, 4,75,
4,70, 4,65, 4,70, 4,65, 4,65 (мм).

24. Пример:

Вариационный ряд:
4,55, 4,59, 4,59, 4,65, 4,65, 4,65,
4,65, 4,70, 4,70, 4,75, 4,75 (мм).

25. Частота -

количество наблюдений
варианты.
ni

26. Относительная частота -

Относительная частота отношение частоты к объему
выборки.
ni
Wi
n

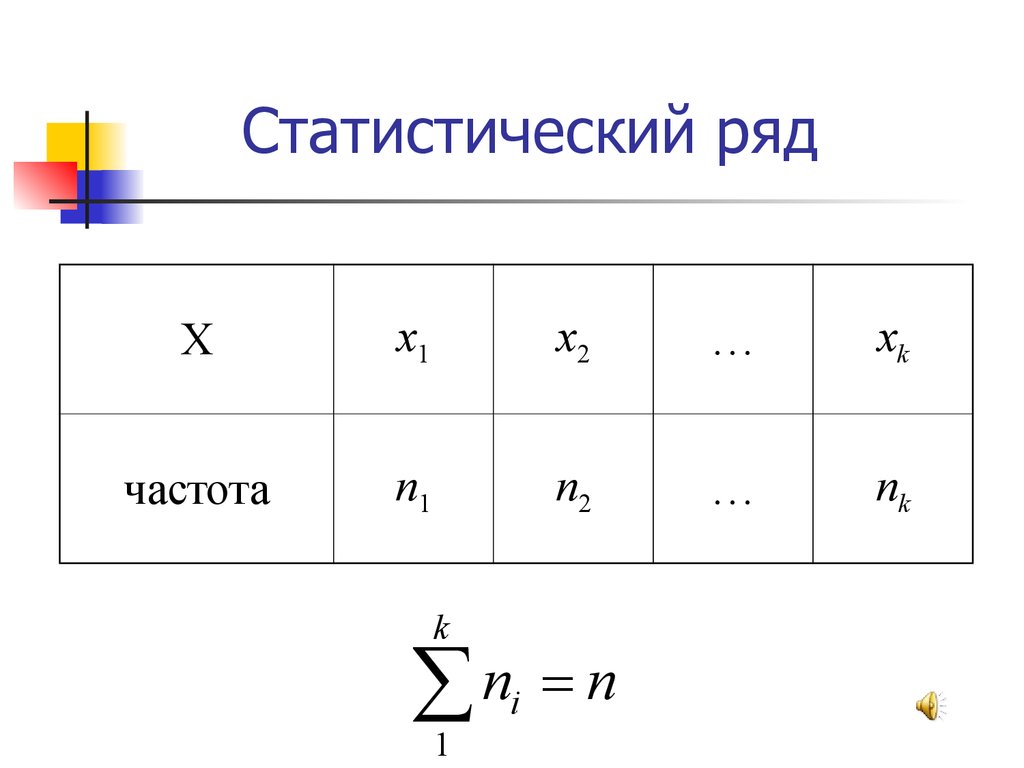
27. Статистический ряд -

перечень вариант и соответствующих
им частот или относительных частот.

28. Статистический ряд

Х
x1
x2
…
xk
частота
n1
n2
…
nk
k
n
i
1
n

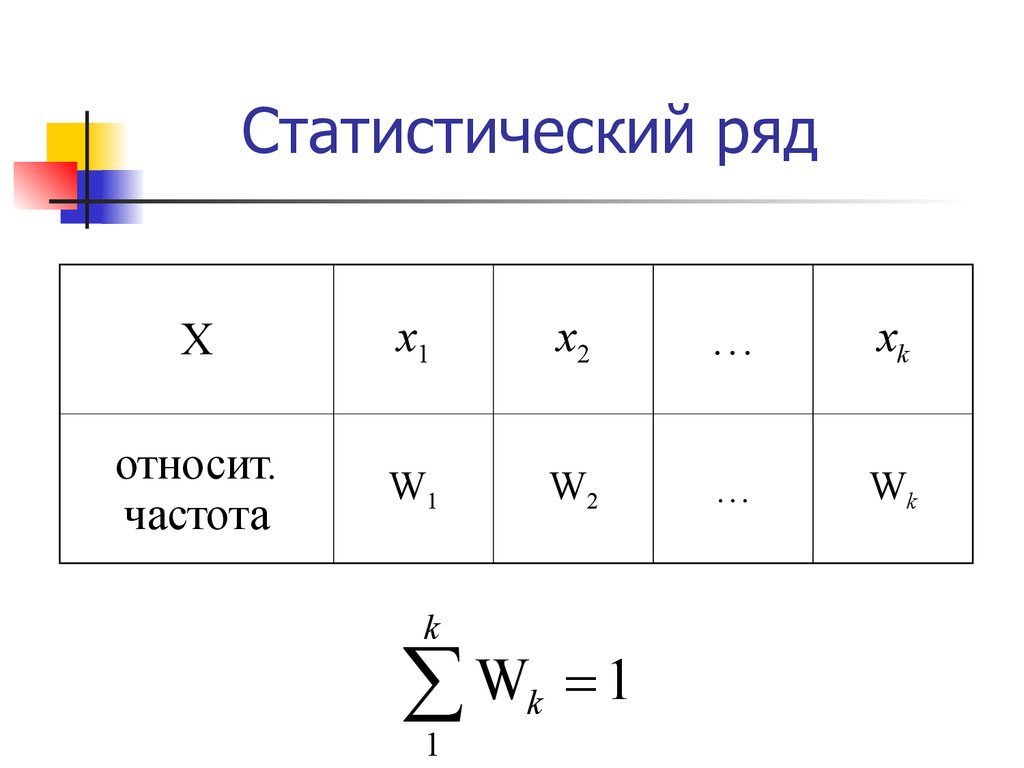
29. Статистический ряд

Х
x1
x2
…
xk
относит.
частота
W1
W2
…
Wk
k
W
k
1
1

30. Статистический ряд

x1
Х
проценты
W1·100% W2·100%
k
W
k
1
x2
…
xk
…
Wk·100%
100% 100%

31. Пример:

хi
4,55
4,59
4,65
4,70
4,75
ni
1
2
4
2
2

32. Пример

(результаты
исследования
рецидивной
преступности
100 осужденных):
не имели повторных судимостей – 50 человек,
по остальным числа повторных судимостей –
1, 1, 1, 2, 3, 1, 1, 1, 1, 2, 2, 1, 2, 1, 1, 1, 1, 1, 2, 3,
1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 2, 2, 1, 2, 1, 3, 4, 1,
1, 1, 1, 1, 1, 1, 1, 3, 1, 1.

33. Пример:

Число повторных
0
1
2
3
4 Итого
судимостей х i
Количество человек
50 35 10
4
1 n =100
(частота) n i
Относительная частота
0,5 0,35 0,1 0
0
1
(wi = n i /n)
Число людей в %
50% 35% 10% 4% 1% 100%
(wi ·100%)

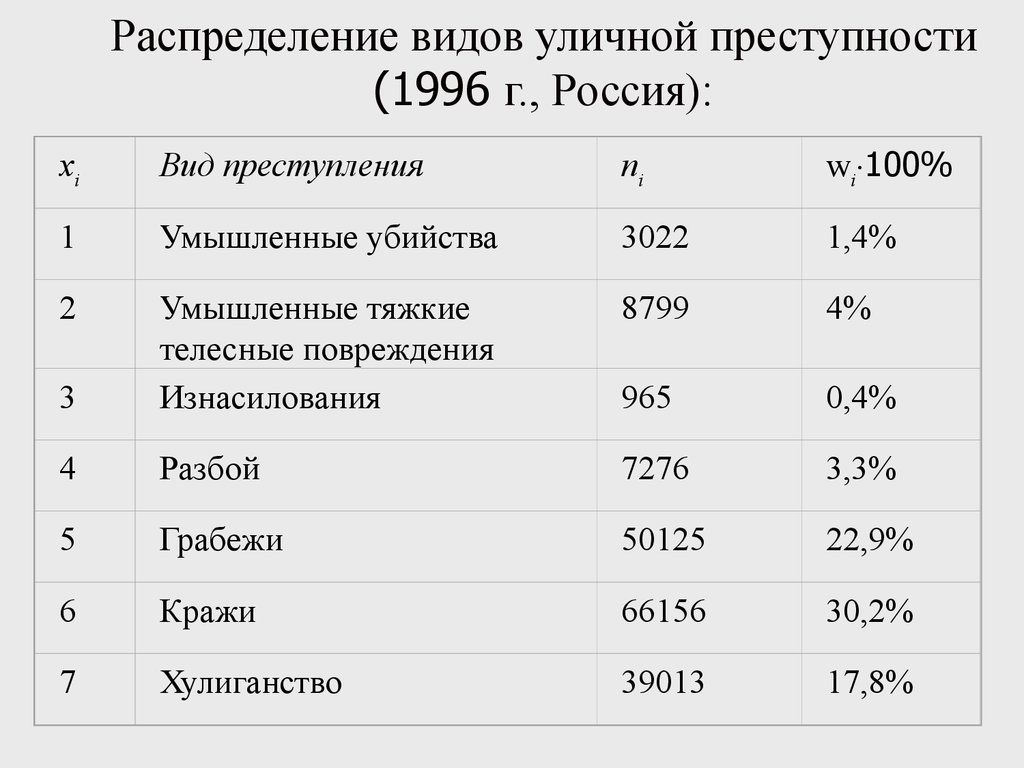
34. Распределение видов уличной преступности (1996 г., Россия):

хi
Вид преступления
ni
wi 100%
1
Умышленные убийства
3022
1,4%
2
8799
4%
3
Умышленные тяжкие
телесные повреждения
Изнасилования
965
0,4%
4
Разбой
7276
3,3%
5
Грабежи
50125
22,9%
6
Кражи
66156
30,2%
7
Хулиганство
39013
17,8%

35.

При дискретной вариации значения
признака отличаются друг от друга на
некоторое (часто целое) число.
При непрерывной вариации
значения признака могут отличаться
на сколь угодно малую величину.

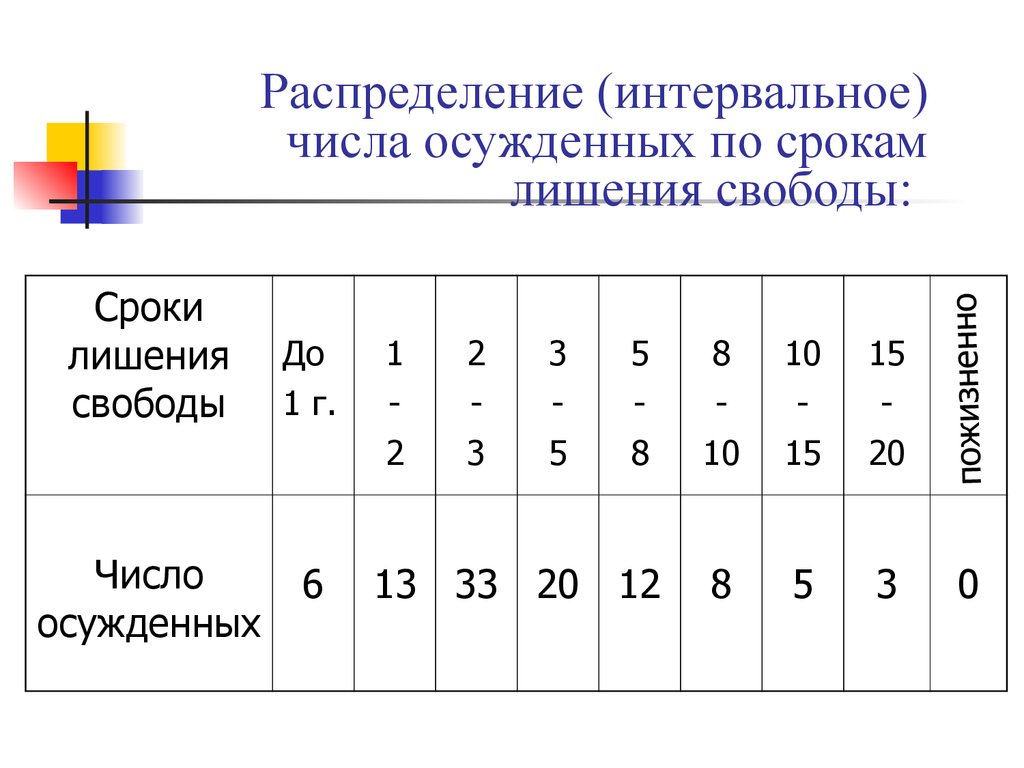
36. Распределение (интервальное) числа осужденных по срокам лишения свободы:

Сроки
лишения
свободы
Число
осужденных
До
1 г.
6
1
2
2
3
3
5
5
8
13 33 20 12
8
10
10
15
15
20
пожизненно
Распределение (интервальное)
числа осужденных по срокам
лишения свободы:
8
5
3
0

37. Величина интервала

xmax xmin
h
2 ln n
хmax и xmin – наибольшее и наименьшее
значения вариант;
n – число элементов в исследуемой
совокупности.

38. Полигон

строят из отрезков, соединяющих точки
плоскости, координатами которых являются
значения вариант хi и соответствующие частоты
или относительные частоты (часто выраженные
в процентах).

39.

Количество человек
Число повторных
судимостей х i
Количество человек
(частота) n i
0
1
2
3
4
50
35
10
4
1
50
45
40
35
30
25
20
15
10
5
0
0
1
2
3
Число повторных судимостей
4

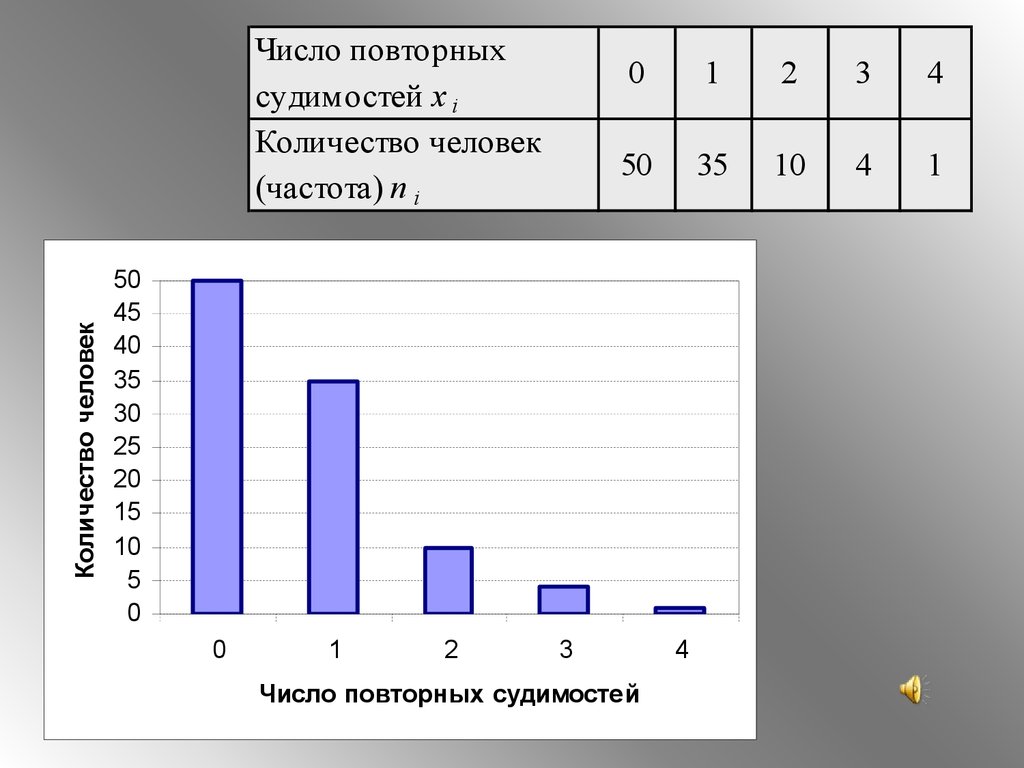
40. Гистограмма

строится из равных по ширине прямоугольников,
высоты которых пропорциональны
соответствующей частоте (или относительной
частоте).

41.

Количество человек
Число повторных
судимостей х i
Количество человек
(частота) n i
0
1
2
3
4
50
35
10
4
1
50
45
40
35
30
25
20
15
10
5
0
0
1
2
3
Число повторных судимостей
4

42. Кумулята

Для того чтобы построить кумуляту (кумулятивную
кривую), называемую часто эмпирической функцией
распределения, необходимо соединить точки,
координатами которых являются значения вариант хi и
накопленные частоты (относительные частоты).
x1 – n1,
x2 – n1 n2 ,
x3 – n1 n2 n3 ,
и т.д.

43.

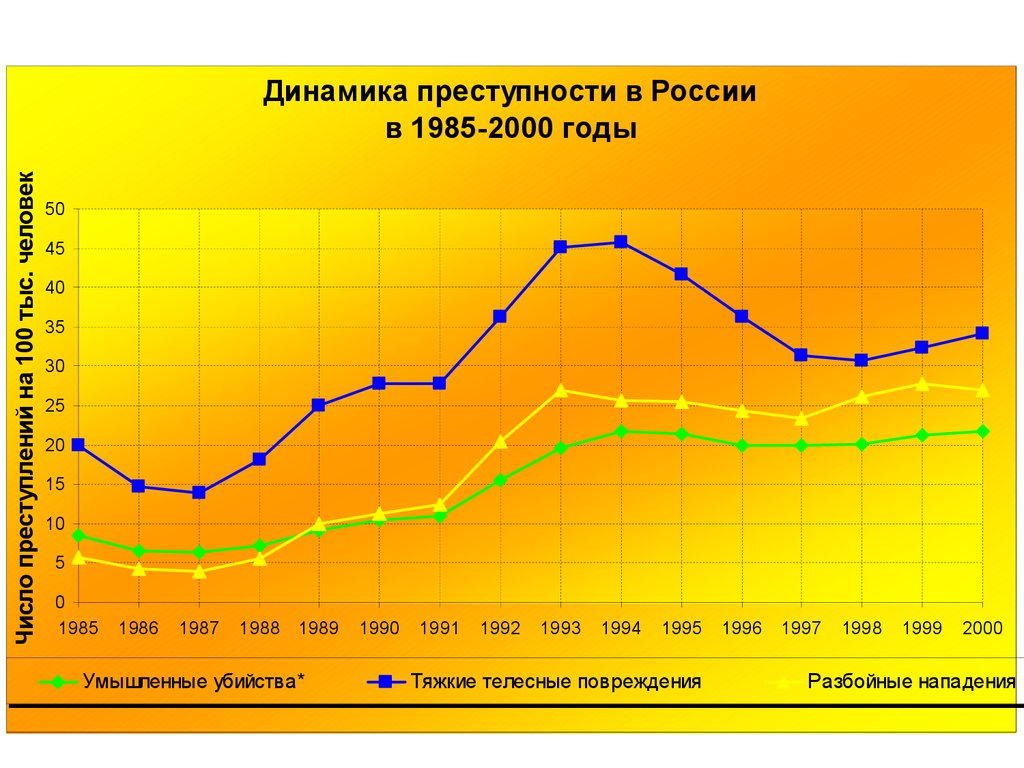
44.

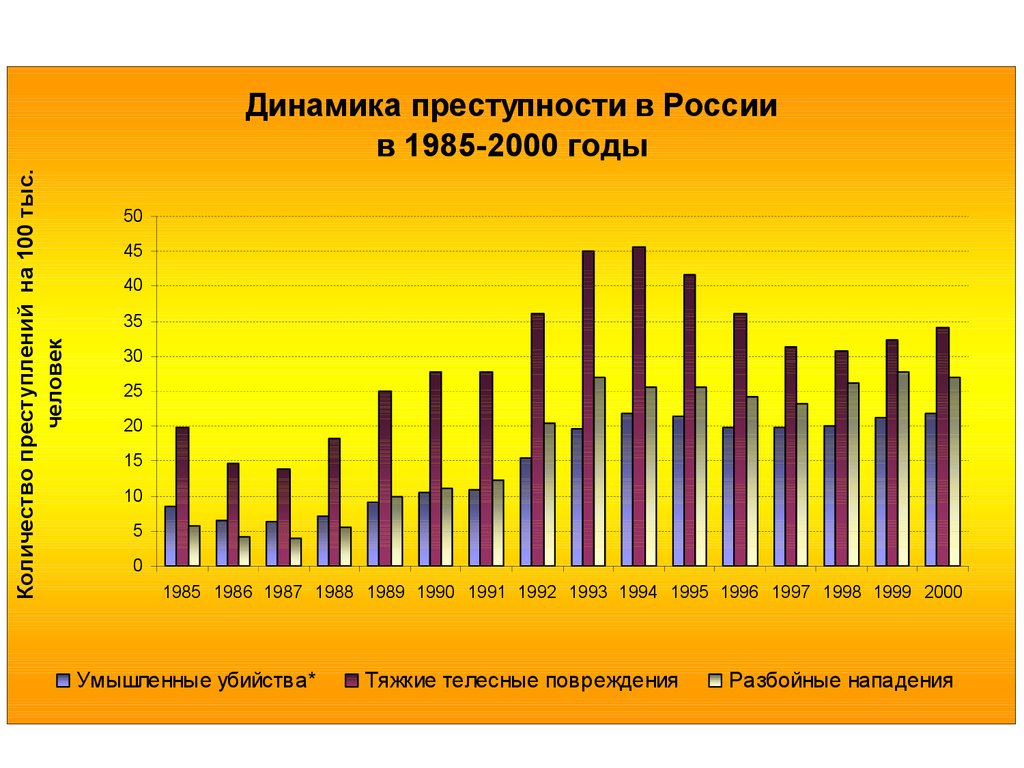
Число преступлений на 100 тыс. человек
Динамика преступности в России
в 1985-2000 годы
50
45
40
35
30
25
20
15
10
5
0
1985
1986
1987
1988
1989
Умышленные убийства*
1990
1991
1992
1993
1994
1995
Тяжкие телесные повреждения
1996
1997
1998
1999
2000
Разбойные нападения

45.

Количество преступлений на 100 тыс.
человек
Динамика преступности в России
в 1985-2000 годы
50
45
40
35
30
25
20
15
10
5
0
1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000
Умышленные убийства*
Тяжкие телесные повреждения
Разбойные нападения

46. 3. Основные выборочные и генеральные харктеристики

47.

хi
x1
x2
…
xk
ni
n1
n2
…
nk
n1 n2 ... nk n

48. Выборочной средней

называется среднее арифметическое
значений признака выборочной
совокупности.
x

49.

хi
x1
x2
…
xk
ni
n1
n2
…
nk
n1 n2 ... nk n
n1 x1 n2 x2 ... nk xk
x
n

50. Пример:

Число повторных
0
1
2
3
4 Итого
судимостей х i
Количество человек
50 35 10
4
1 n =100
(частота) n i
Относительная частота
0,5 0,35 0,1 0
0
1
(wi = n i /n)
Число людей
% 1 35 2 10 3 4 4 1
0 в50
50% 35% 10% 4% 1%
100%
x
0
,
71
(wi ·100%)
100

51. Медианой ML

называется варианта признака, находящаяся
в центре вариационного ряда.
n=2а+1 - нечетное
M L x a 1
n=2а - четное
x a x a 1
ML
2

52. Пример:

4,55, 4,59, 4,59, 4,65, 4,65, 4,65,
4,65, 4,70, 4,70, 4,75, 4,75 (мм).
n = 11= 2·5+1
M L x6 4,65мм

53. Пример:

Число повторных
0
1
2
3
4 Итого
судимостей х i
Количество человек
50 35 10
4
1 n =100
(частота) n i
Относительная частота
0,5 0,35
0,1 x0 =10
1
x
=0,
100 = 2 50,
50
51
(wi =nn =
i /n)
Число людей в %
50%
35%
10% 4% 1% 100%
0
1
(wi ·100%)
ML
2
0,5

54. Выборочной модой

ˆ
Mo
называется элемент выборки, обладающий
наибольшей частотой.

55. Пример:

4,55, 4,59, 4,59, 4,65, 4,65, 4,65,
4,65, 4,70, 4,70, 4,75, 4,75 (мм).
Mˆ o 4,65 мм

56. Пример:

Число повторных
0
1
2
3
4 Итого
судимостей х i
Количество человек
50 35 10
4
1 n =100
(частота) n i
Относительная частота
0,5 0,35 0,1 0
0
1
(wi = n i /n)
Число людей в %
50% 35% 10% 4% 1% 100%
(wi ·100%)
Mˆ o 0

57. Размахом выборки

Rˆ
называют разность между максимальным и
минимальным значениями выборки
Rˆ xmax xmin

58. Пример:

4,55, 4,59, 4,59, 4,65, 4,65, 4,65,
4,65, 4,70, 4,70, 4,75, 4,75 (мм).
Rˆ 4,75 4,55 0,20( мм)

59. Пример:

Число повторных
0
1
2
3
4 Итого
судимостей х i
Количество человек
50 35 10
4
1 n =100
(частота) n i
Относительная частота
0,5 0,35 0,1 0
0
1
(wi = n i /n)
ˆ 4 0 4
R
Число людей в %
50% 35% 10% 4% 1% 100%
(wi ·100%)

60. ОТКЛОНЕНИЕМ i-ой варианты от среднего

называют разность между конкретным i-м
значением признака и средней величиной:
xi xi x

61. Пример:

x 0,71
Число повторных
0
1
2
3
4
судимостей х i
Количество человек
50 35 10
4
1
(частота) n i
Относительная частота
0,5 0,35 0,1 0
0
x
0
0
,
71
0
,
71
1
(wi = n i /n)
x4 3 0,71
Число людей в %
x2 1 0,71 0,29 50% 35% 10% 4% 1%
(wi ·100%)
x3 2 0,71 1,29
Итого
n =100
1
2,29
100%
x5 4 0,71 3,29

62. Выборочной дисперсией

называется среднее арифметическое квадратов
отклонений:
2
2
2
x1 n1 x2 n2 ... xk nk
ˆ
D( X )
n

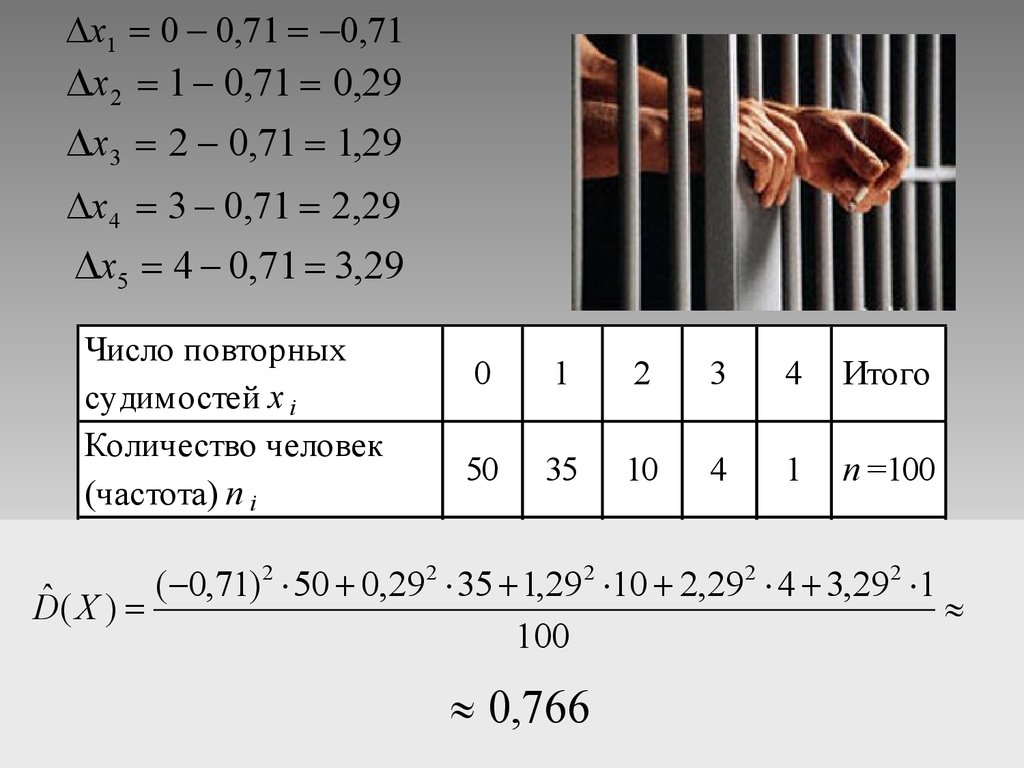
63.

x1 0 0,71 0,71
x2 1 0,71 0,29
x3 2 0,71 1,29
x4 3 0,71 2,29
x5 4 0,71 3,29
Число повторных
0
1
2
3
4 Итого
судимостей х i
Количество человек
50 35 10
4
1 n =100
(частота) n i
Относительная частота
0 2 0
12
2
2 0,5 0,352 0,1
(
0
,
71
)
50
0
,
29
35
1
,
29
10
2
,
29
4
3
,
29
1
(wi = n i /n)
ˆ
D( X )
Число людей в %
100
50% 35% 10% 4% 1% 100%
(wi ·100%)
0,766

64. Выборочное среднее квадратическое отклонение

ˆ
ˆ
D( X )

65. Пример:

Dˆ ( X ) 0,766
Число повторных
0
1
2
3
4 Итого
судимостей х i
Количество человек
50 35 10
4
1 n =100
(частота) n i
Относительная частота
0,5 0,35 0,1 0
0
1
(wi = n i /n)
Число людей
ˆ (вX%) 050%
,7659
0,875
35% 10%
4% . 1% 100%
(wi ·100%)

66. Дисперсия и среднее квадратическое отклонение характеризуют рассеяние значений количественного признака выборочной совокупности вокру

Дисперсия и среднее квадратическое
отклонение характеризуют рассеяние значений
количественного признака выборочной
совокупности вокруг среднего значения
ДИСПЕРСИЯ
РАССЕЯНИЕ

67. Коэффициент вариации

отношение среднего квадратического
отклонения к выборочной средней,
выраженное в процентах:
ˆ ( X )
V (X )
100%
x

68. Пример:

ˆ ( X ) 0,875
x 0,710
Число повторных
0
1
2
3
4 Итого
судимостей х i
Количество человек
50 35 10
4
1 n =100
(частота) n i
Относительная частота
0,5 0,35 0,1 0
0
1
(wi = n i /n)
0,875
ˆ
Число людей
в
%
V ( x)
123
50% 100
35%%10%
4%%1% 100%
0,710
(wi ·100%)

69.

Аналогичные характеристики
генеральной совокупности
называются генеральными
характеристиками.

70. Статистические оценки параметров распределения

n ˆ
D*(X )
D( X )
n 1
*(X ) D *(X )
n<30

71. Пример:

Dˆ ( X ) 0,766
ˆ ( X ) 0,875.
( 0,71) 2 50 0,29 2 35 1,29 2 10 2,29 2 4 3,29 2 1
D *(X )
99
0,774
* ( X ) 0,774 0,880

72. Статистика есть наука о том, как, не умея мыслить и понимать, заставить делать это цифры. В. О. Ключевский

Статистика есть наука о том,
как, не умея мыслить и