Метод параллельного проектирования

1. Нагнибедовский Артём 9ИС2.18К

2. Стереометрия – это геометрия в пространстве. Нам необходимо уметь изображать геометрические фигуры, причем все чертежи мы

Для этого
применяется метод параллельного проектирования.
Выясним его суть на примере простейшей геометрической фигуры –
точки.
Итак, у нас есть геометрическая фигура в пространстве – точка А.
А

3.

Выберем в пространстве произвольную плоскость (плоскость проекций)
и любую прямую a∩ (она задает направление параллельного проектирования).
а
А

4.

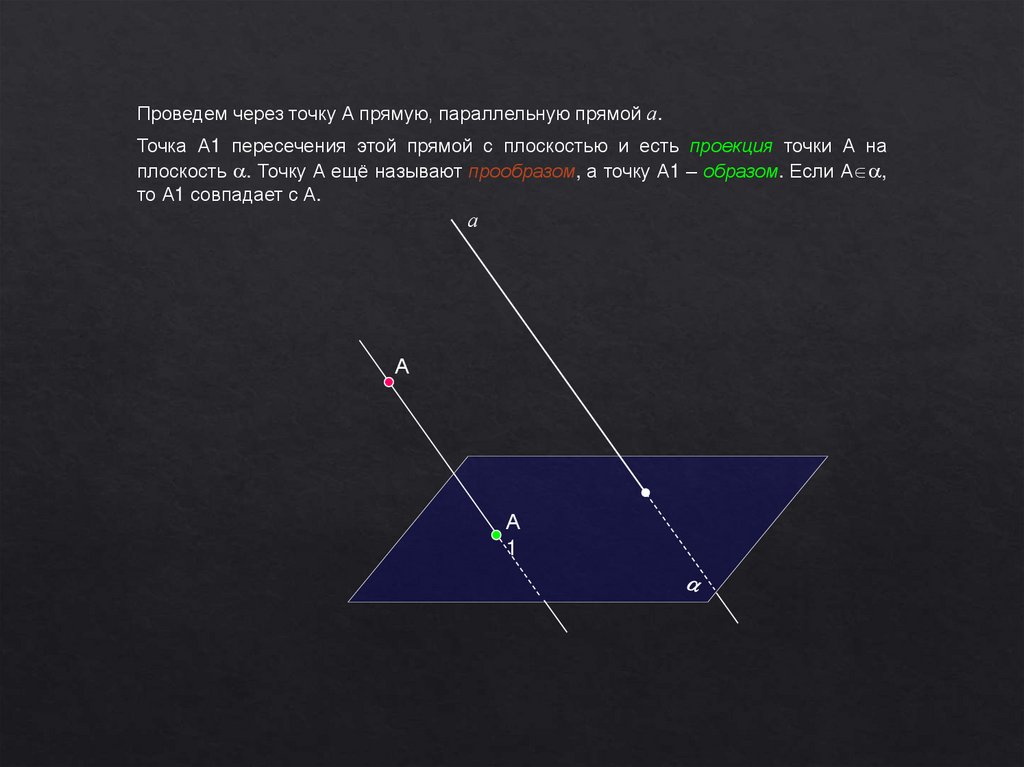
Проведем через точку А прямую, параллельную прямой а.
Точка А1 пересечения этой прямой с плоскостью и есть проекция точки А на
плоскость . Точку А ещё называют прообразом, а точку А1 – образом. Если А ,
то А1 совпадает с А.
а
А
А
1

5. Рассматривая любую геометрическую фигуру как множество точек, можно построить в заданной плоскости проекцию данной фигуры.

а
Наглядным примером параллельного проектирования является отбрасываемая
любым объектом(прообраз) в пространстве тень(образ) от солнечных
лучей(направление параллельного проектирования) на Земле(плоскость
проекций).

6.

При параллельном проектировании не выбирают направление параллельного
проектирования параллельно плоскости проекции
а
А

7.

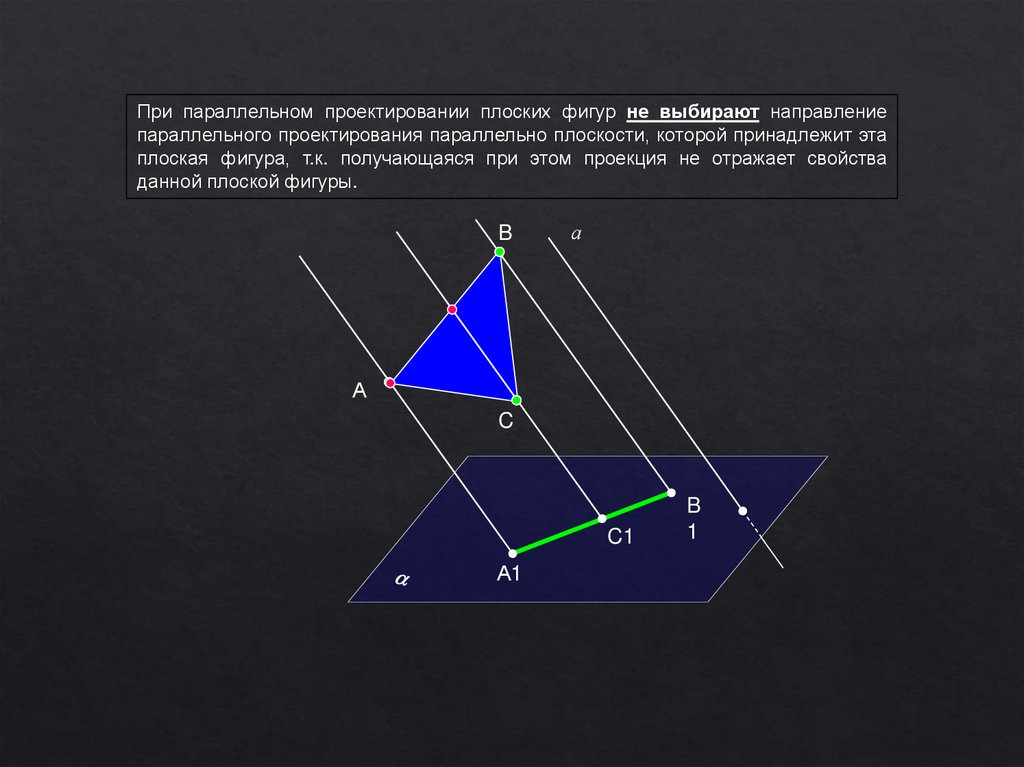
При параллельном проектировании плоских фигур не выбирают направление
параллельного проектирования параллельно плоскости, которой принадлежит эта
плоская фигура, т.к. получающаяся при этом проекция не отражает свойства
данной плоской фигуры.
B
а
А
C
C1
А1
B
1

8.

Если направление параллельного проектирования перпендикулярно
плоскости проекций, то такое параллельное проектирование называется
ортогональным (прямоугольным) проектированием.
B
а
А
C
А1
C1
B1
Ортогональная проекция - частный случай параллельной проекции, когда
ось или плоскость проекций перпендикулярна (ортогональна) направлению
проектирования

9.

Если плоскость проекций и плоскость, в которой лежит данная фигура
параллельны ( ||(АВС)), то получающееся при этом изображение равно
прообразу.
B
а
А
C
B1
А1
C1

10.

Параллельное проектирование обладает свойствами:
1) параллельность прямых (отрезков, лучей) сохраняется;
B
а
D
A
C
B1
D1
A1
AB ||CD => A1B1 ||C1D1
C1

11.

Параллельное проектирование обладает свойствами:
1)
параллельность прямых (отрезков, лучей) сохраняется;
2) отношение длин отрезков, лежащих на параллельных или на одной прямой
сохраняется;
B
а
М
D
A
C
B1
М1
D1
A
1
C1
Если, например, АВ=2CD, то А1В1=2C1D1 или
AM A' M '
MB M ' B'

12.

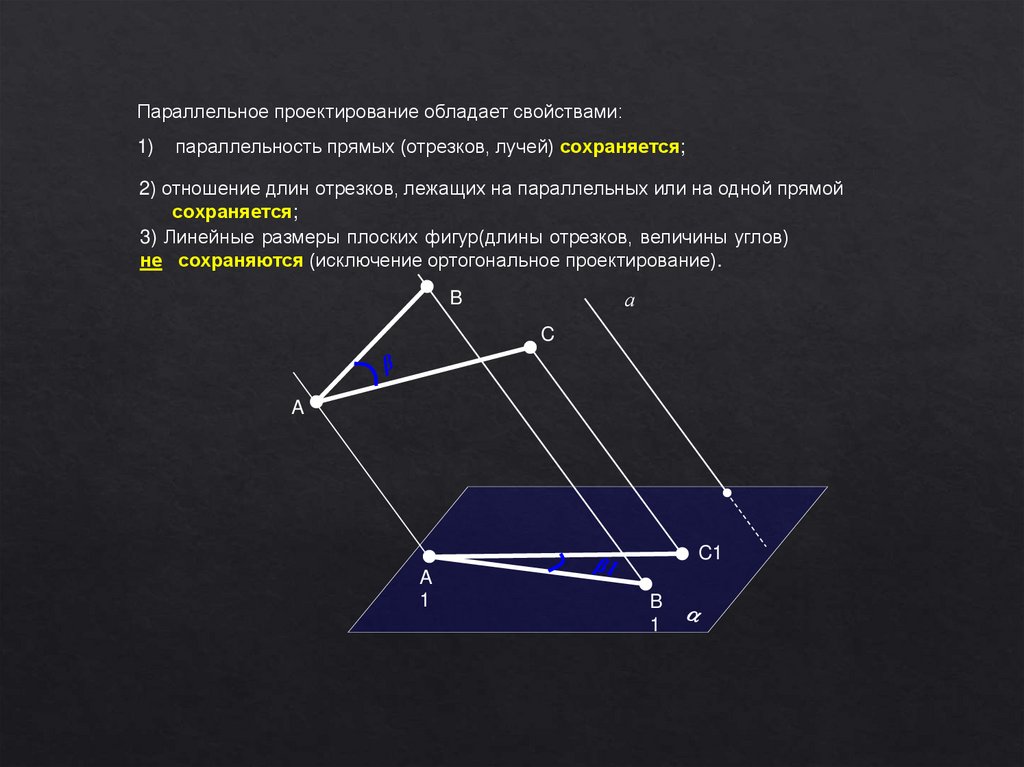
Параллельное проектирование обладает свойствами:
1)
параллельность прямых (отрезков, лучей) сохраняется;
2) отношение длин отрезков, лежащих на параллельных или на одной прямой
сохраняется;
3) Линейные размеры плоских фигур(длины отрезков, величины углов)
не сохраняются (исключение ортогональное проектирование).
а
B
C
A
C1
A
1
B
1

13.

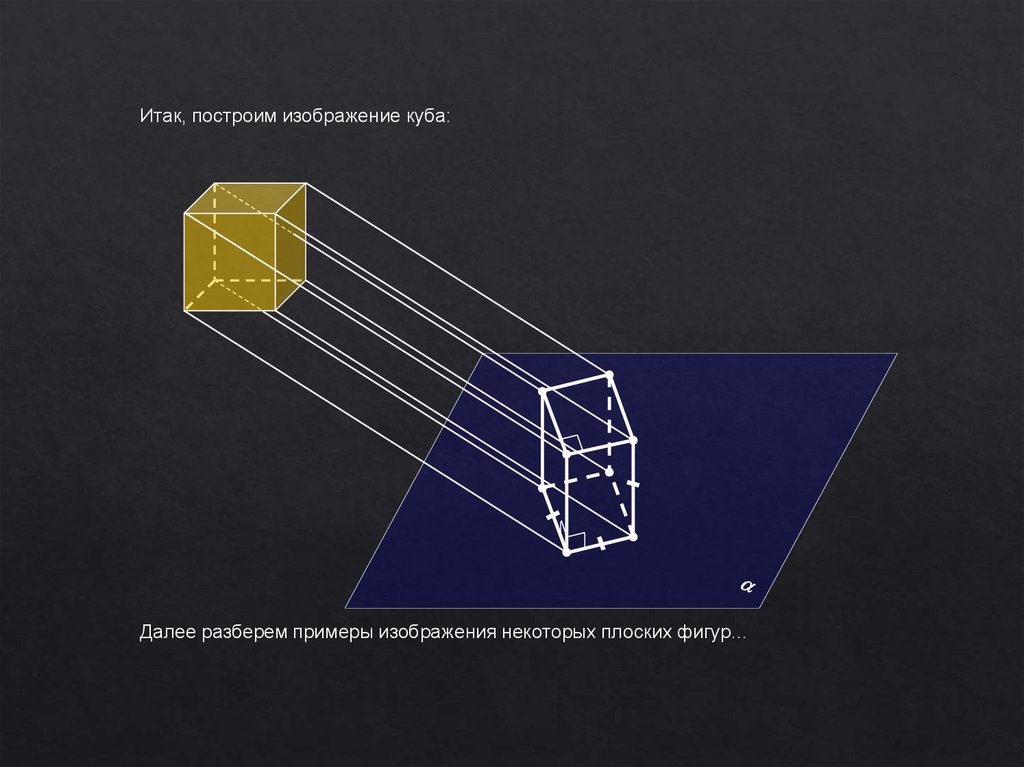
Итак, построим изображение куба:
Далее разберем примеры изображения некоторых плоских фигур…

14.

Фигура в пространстве
Произвольный треугольник
Прямоугольный треугольник
Равнобедренный
треугольник
Её изображение на плоскости
Произвольный треугольник
Произвольный треугольник
Произвольный треугольник

15.

Фигура в пространстве
Равносторонний треугольник
Параллелограмм
Прямоугольник
Её изображение на плоскости
Произвольный треугольник
Произвольный параллелограмм
Произвольный параллелограмм

16.

Фигура в пространстве
Квадрат
Ромб
Трапеция
Её изображение на плоскости
Произвольный параллелограмм
Произвольный параллелограмм
Произвольная трапеция

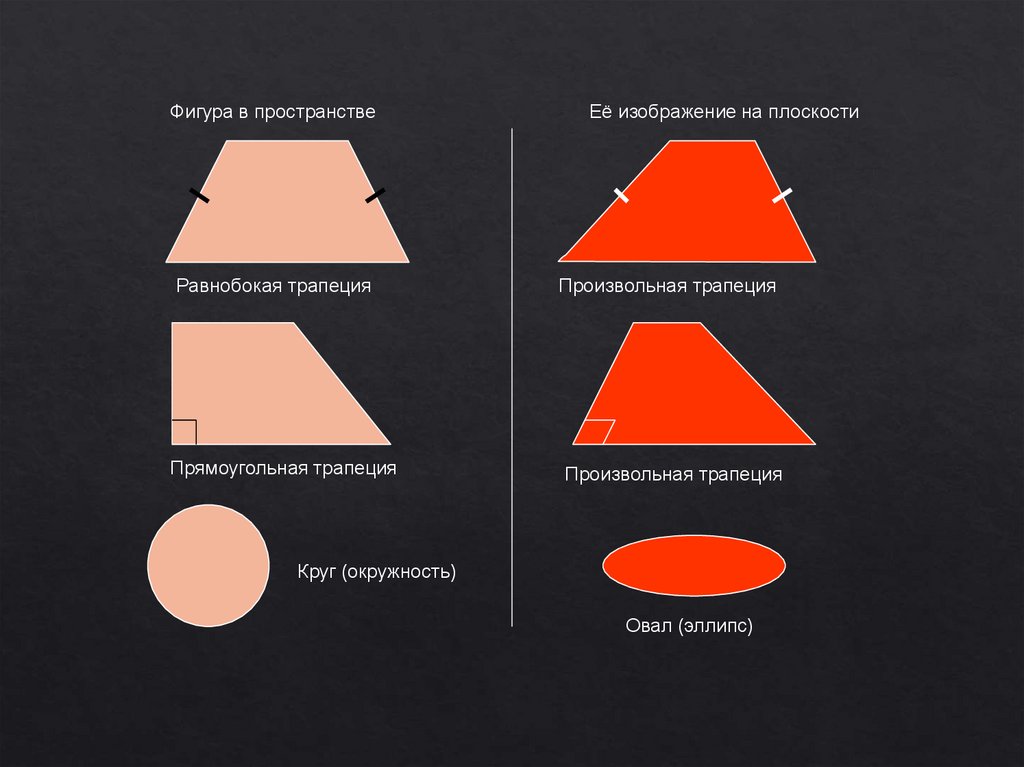
17.

Фигура в пространстве
Равнобокая трапеция
Прямоугольная трапеция
Её изображение на плоскости
Произвольная трапеция
Произвольная трапеция
Круг (окружность)
Овал (эллипс)

18.

19.

Следовательно, для треугольника теорема верна.
Пусть теперь есть многоугольник ABCD. Разобьем его на треугольники. Каждый
треугольник, у которого нет стороны, параллельной плоскости проекции,
разобьем на два треугольника с общей стороной, параллельной плоскости
проекции. Получаем что для каждого треугольника Δ и его проекции Δ` в
плоскости α верно равенство
Сложим все эти равенства почленно. Получим