Аттестационная работа: Исследовательская деятельность на уроках математики

1. Аттестационная работа

Слушателя курсов повышения квалификации по программе:
«Проектная и исследовательская деятельность как способ
формирования метапредметных результатов обучения в
условиях реализации ФГОС»
________________Шапошникова Марина Анатольевна___
Фамилия, имя, отчество
____________________________________________________
_МБОУСОШ №24 г. Уссурийск__
Образовательное учреждение, район
На тему:
Исследовательский деятельность на уроках
математики
1

2. Исследовательский подход к введению математических понятий.

Формирование научных понятий – одна из главных задач обучения
математике в школе. Формирование конкретного понятия тесно связано с
усвоением учащимися соответствующего математического объекта и
возникновением общего представления о нем. Усвоить понятие – значит
усвоить систему знаний о некотором объекте и научиться использовать их
в деятельности.
Исследовательский подход к введению нового понятия направлен на
формирование нового понятия в целом (как системы взаимосвязанных
логически упорядоченных суждений). При этом можно организовать
познавательную деятельность учащихся таким образом, чтобы
воспроизвести (в некоторой степени) деятельность ученого-математика,
направленную на изучение нового объекта и образование понятия.

3. Исследовательский подход включает следующие этапы:

постановка цели деятельности;
эмпирическое изучение нового математического объекта, поиск его свойств;
формулирование найденных свойств в виде гипотез;
введение нового термина, определение математического объекта;
проверка истинности высказанных предположений путем отыскания их доказательств;
поиск признаков исследуемого объекта (рассмотрение обратных утверждений);
уточнение логических связей между суждениями, систематизация содержания нового
понятия, усвоение этого содержания;
обучение применению нового понятия в деятельности: решение опорных задач,
выделение общих приемов деятельности, способствующих применению понятия;
применение понятия в нестандартных ситуациях

4.  Урок геометрии в 8 классе по теме: «Равнобедренная трапеция». .

Урок геометрии в 8 классе по теме:
«Равнобедренная трапеция».
изучить понятие равнобедренной трапеции, сформулировать и
. Цель:
доказать ее свойства, применить понятие равнобедренной трапеции в
решении задач

5.

Класс разбит на группы, которые получают чертежи равнобедренной трапеции.
Назвать основные элементы трапеции: стороны, углы, диагонали.
Сегодня мы изучим этот четырехугольник. Что интересует геометров при изучении фигур в первую очередь?
Соотношения между сторонами и углами.
Какова цель нашего исследования?
Выявить соотношения между элементами трапеции, изучить другие особенности этой фигуры.
Возьмите инструменты, измерьте стороны, углы, диагонали.
Сформулируйте гипотезы о свойствах этих элементов
Сформулируем другие особенности трапеции.
Высоты, проведенные из вершин меньшего основания, отсекают от нее равные прямоугольные треугольники.
Диагонали разбивают трапецию на два равных и два равнобедренных треугольника.
Можно ли считать, что мы изучили фигуру?
Нет. У нас только гипотезы.
Сформулируем и докажем теоремы.

6.

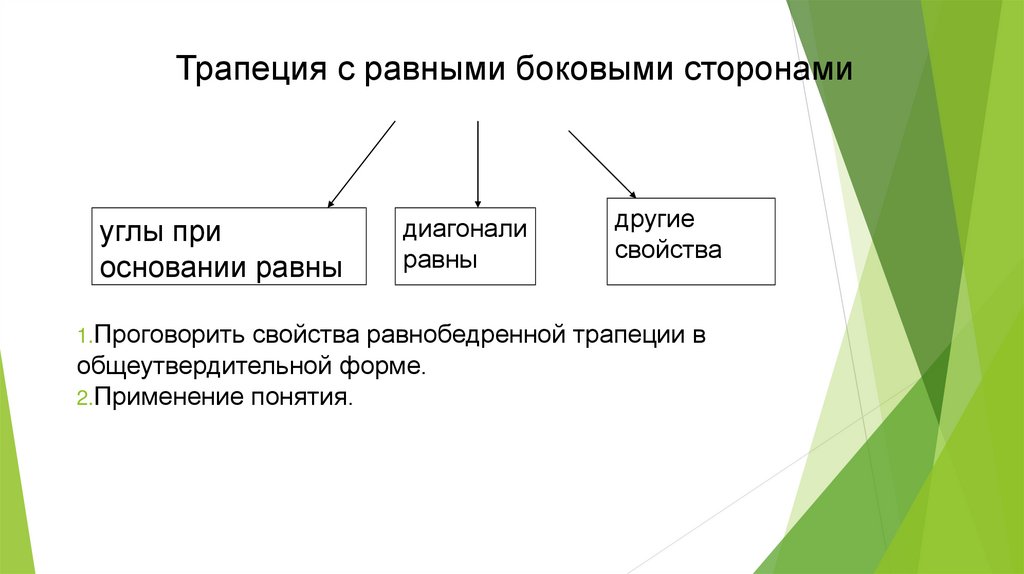
Трапеция с равными боковыми сторонами
углы при
основании равны
1.Проговорить
диагонали
равны
другие
свойства
свойства равнобедренной трапеции в
общеутвердительной форме.
2.Применение понятия.

7. Применение полученных знаний при решении задач:

Задача 1. В равнобедренной трапеции основания равны
4 и 6 диагональ равна 73 . Найти боковую сторону.
Задача 2. В равнобедренной трапеции с углом 600,
разность оснований равна 5 см. Найти боковую сторону
трапеции
Задача 3. Диагонали равнобедренной трапеции
перпендикулярны и равны, а ее меньшее основание 5
см. Найти большее основание трапеции.