Три режими в нелінійній моделі популяції - вплив нелінійності на процес коливань

1.

Три режими в нелінійній моделі
популяції - вплив нелінійності на
процес коливань

2.

Популяція – це сукупність
організмів одного виду, що займають
обмежений ареал (територія
поширення якогось об'єкта або
явища), мають спільне походження за
фенотипом(сукупність
характеристик, властивих індивіду на
певній стадії розвитку) та
географічно ізольовані від інших
популяцій даного виду, можуть
вільно схрещуватися і дають плодюче
потомство.
Чисельність популяції — загальна
кількість особин на даній
території або в даному об’ємі
(води, ґрунту, повітря), які
належать до однієї популяції.
Розрізняють неперіодичні (такі,
що рідко спостерігаються) і
періодичні (постійні) коливання
чисельності популяцій.
Фактори, які впливають на
чисельність популяції: повінь,
пожежа, град, раптові морози,
посуха, бурелом, надмірне
застосування хімічних препаратів,
реконструкція ландшафту,
вселення нових видів хижаків,
паразитів, епідемії — все це може
призвести до повної її загибелі.
Типові приклади різних
популяцій : рослин(сосна, ялина,
ялиця, кипарис, кедр, тис,
секвойя, модрина),
тварин(ссавці(зубр,лев,жираф,їжа
к), птахи, риби, комахи,
павукоподібні, молюски, морські
зірки і т.д), бактерій.

3. Три режими в нелінійній моделі популяції

Традиційно областю застосування математичних моделей є теорія
розвитку біологічних популяцій. Дана теорія розглядає з однієї
точки зору різні аспекти основних закономірностей зміни
чисельності популяцій, в тому числі, і клітин, що мешкають як в
природних умовах так і в лабораторних. Основні особливості
пов’язані з факторами, що лімітують ріст середовища, та з
взаємодією різних видів у процесі росту

4.

Моделі популяцій відразу ж стають нелінійними, якщо зважувати
на те ,що обмеженість доступних популяції ресурсів необхідно
обов’язково враховувати. Будуючи такі моделі, вважають, що:
1) існує «рівноважна»
чисельність популяції Np,
котру може забезпечити
навколишнє середовище (з
погляду сьогодення);
2) швидкість зміни чисельності
популяції пропорційна цій
чисельності, помноженій (на
відміну від моделі Мальтуса) на
величину відхилення її від
рівноважного значення
чисельності

5. Модель природного росту чисельності популяції (модель Мальтуса)

Однією з важливих проблем екології є динаміка чисельності популяції.
Нехай маємо деяку реальну популяцію, що складається з особин
одного виду, і потрібно знайти закон зміни її чисельності.
Основні допущення.
1. Існують тільки процеси розмноження і природної загибелі, швидкості
яких пропорційні чисельності особин у даний момент часу.
2. Не враховуємо біохімічні, фізіологічні процеси.
3. Немає боротьби між особинами за місце проживання, за їжу
(нескінченно великий простір і кількість їжі).
4. Розглядаємо тільки одну популяцію, немає хижаків.
Уведемо величини моделі :
x - чисельність популяції в момент t;
R - швидкість розмноження, g - коефіцієнт розмноження;
S - швидкість природної загибелі, s - коефіцієнт природної загибелі;
dx/dt - швидкість зміни чисельності популяції, e - коефіцієнт росту.
Тоді R = gx, S = -σx.

6.

Складемо диференціальне рівняння балансу. Зміна чисельності особин
в одиницю часу визначається кількістю породжених за цей час і
померлих:
dx
dx
( y )x
x
або
dt
dt
Початкова умова: при t = 0
x
чисельність особин x = x0
Вирішимо рівняння:
I
dx
x0 x 0 dt
x
x
ln
t
x0
x
x0
x0
a
t
б
Аналіз рішення.
а) e < 0 (при s > g), тобто швидкість загибелі більше швидкості розмноження.
Чисельність особин згодом упаде до нуля
б) e> 0 (при s> g), тобто швидкість розмноження більше швидкості загибелі.
Чисельність особин необмежено росте згодом
в) e = 0 (при s= g), тобто швидкість загибелі дорівнює швидкості розмноження.
Чисельність особин не змінюється, залишаючись на початковому рівні.
Модель при e > 0 адекватна реальності лише до визначених значень часу.
Відповідно до даної моделі, що розглядає зменшення чисельності особин тільки
за рахунок природної загибелі, їхня чисельність повинна нескінченно зростати
згодом 0що не відповідає реальності. При великій кількості особин можливе
зменшення їхньої чисельності за рахунок інших механізмів, наприклад, за
рахунок боротьби за місце проживання, за їжу.
t

7. Модель зміни чисельності популяції з урахуванням конкуренції між особинами (модель Ферх’юльста)

Нехай існує боротьба між особинами, наприклад, за місце
проживання, тим самим додається додаткове джерело
загибелі. Вважаючи, що швидкість загибелі за рахунок
конкуренції між особинами пропорційна імовірності
зустрічей двох особин, можна записати S = -δx×x – σx (δ коефіцієнт пропорційності).

8.

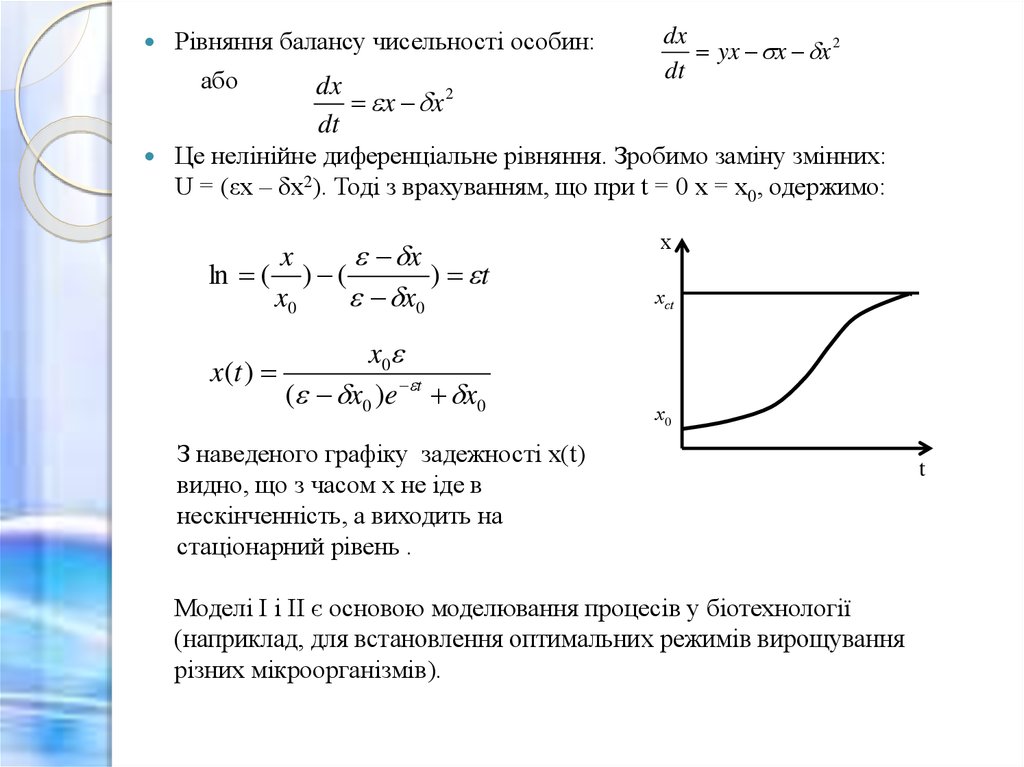
Рівняння балансу чисельності особин:
або
dx
x x 2
dt
dx
yx x x 2
dt
Це нелінійне диференціальне рівняння. Зробимо заміну змінних:
U = (εx – δx2). Тоді з врахуванням, що при t = 0 x = x0, одержимо:
x
x
ln ( ) (
) t
x0
x0
x0
x(t )
( x0 )e t x0
х
хсt
х0
З наведеного графіку задежності x(t)
видно, що з часом x не іде в
нескінченність, а виходить на
стаціонарний рівень .
Моделі I і II є основою моделювання процесів у біотехнології
(наприклад, для встановлення оптимальних режимів вирощування
різних мікроорганізмів).
t

9. Модель "хижак-жертва" (модель Вольтерра)

Модель "хижак-жертва" (модель Вольтерра)
Серед допущень, введених у моделі I, знімемо допущення 4. Нехай у
деякому просторі живуть два види особин: зайці (жертви) і рисі
(хижаки). Зайці харчуються рослинною їжею, що є завжди в достатній
кількості (між ними відсутня внутрішньовидова боротьба). Рисі
можуть харчуватися тільки зайцями.
Уведемо величини:
x - число жертв у момент t;
у - число хижаків у момент t.
Рівняння балансу між чисельністю народжених і особин, що гинуть:
Жертви:
dx
yx x axy
dt
Хижаки:
dy
xy y
dt
yx
-швидкість розмноження
х
-швидкість природньої смерті
axy
-швидкість смерті за рахунок зустрічі з хижаком
xy
-швидкість розмноження
y
-швидкість природньої смерті

10.

Це складна система нелінійних диференціальних рівнянь. Спочатку
знайдемо стаціонарне рішення x = const, у = const, тобто
dx
0
dt
dx
0
dt
Система диференціальних рівнянь при цьому зводиться до алгебраїчної:
Розглянемо рішення:
xC
С
Спростимо систему рівнянь , припускаючи, що відбулися малі відхилення
чисельності хижаків V(t) і жертв U(t) щодо стаціонарних значень:
x xст U (t )
U xст
y уст V (t ) V уст
Тоді :
U уст
V xст
dU
xст ( ayст ) U ( ayст ) axстV aUV
dt
dV
yст ( xст ) V ( xст ) Uyст UV
dt

11.

Одержимо систему рівнянь
dU
axстV
dt
dV
Uyст
dt
яку легко звести до диференціальних рівнянь другого порядку щодо
змінних U і V:
d 2U
d 2V
U 0
V 0
2
2
dt
dt
Це характерні рівняння для опису гармонійних коливальних процесів.
Рішення рівнянь:
U U max sin t
Відношення амплітуд відхилень:
V Vmax sin( t 0 )
У результаті чисельності особин при малих відхиленнях від
стаціонарних значень рівні:
x(t ) xст U max sin t
Vmax
U max
y(t ) yст Vmax sin( t 0 )
Таким чином, чисельності популяцій x і у зазнають гармонійних
коливань щодо стаціонарних значень з однаковою частотою ,
але зміщені по фазі на φ0.Періодичність зміни чисельності хижаків і
жертв спостерігалася і на досліді. Приведені дослідні дані по кількості
числа добутих шкурок зайців і рисі у Канаді з 1845 по 1935 р

12. Найпростіша лінійна модель динаміки популяцій з урахуванням обмеженості ресурсів. Різні режими в нелінійній моделі популяції.

Нелінійна модель популяції. dN
a( N ) ( N ) N
dt
Нехай
( N ) 0 const
N (a0 N 0 ) N
a( N ) a0 N
Модель справедлива в популяції, де її члени повинні бути зацікавлені в
зростанні.
Обравши відповідні масштаби для N і t, рівняння можна звести до вигляду:
dx
x2 x
dt
або
x x( x 1)
Знову х=0 і х=1 нерухомі точки
dt
dx
1
1
1
1
dx(
) dx(
)
x( x 1)
x x 1
x 1 x

13.

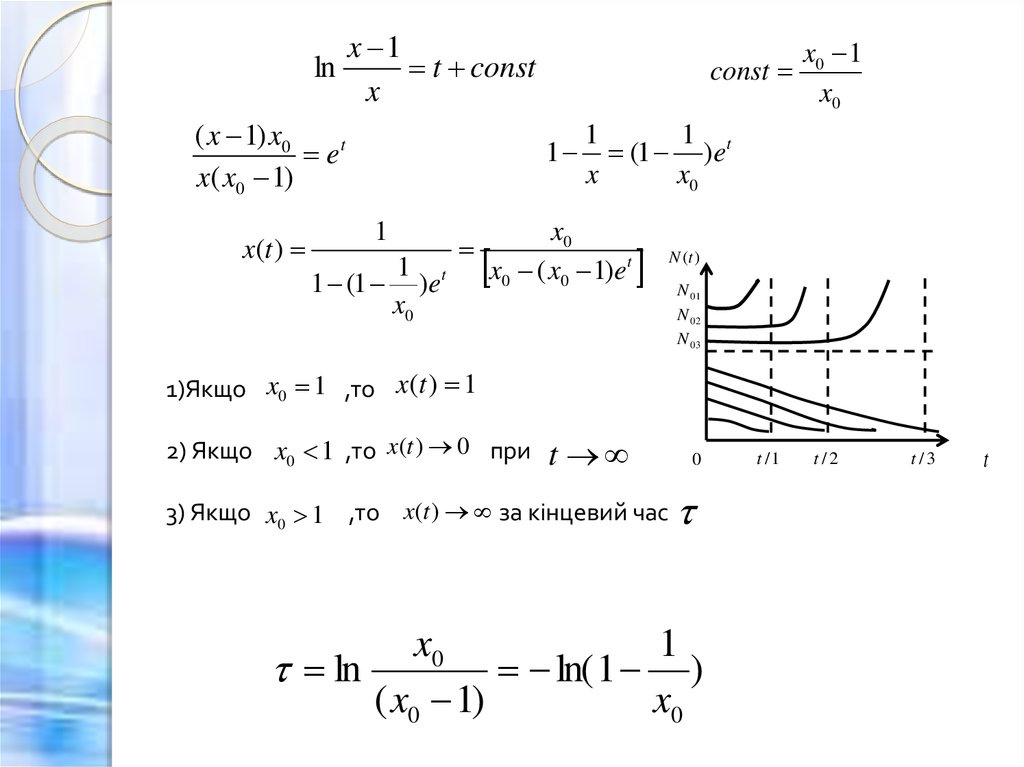
ln
x 1
t const
x
( x 1) x0
et
x( x0 1)
x(t )
const
1
1
1
1 (1 )et
x0
x0 1
x0
1
1
(1 )et
x
x0
x0
x0 ( x0 1)et
N (t )
N 01
N 02
N 03
1)Якщо x0 1 ,то x (t ) 1
2) Якщо x0 1 ,то x(t ) 0 при
t
3) Якщо x0 1 ,то x(t ) за кінцевий час
0
x0
1
ln
ln( 1 )
( x0 1)
x0
t /1
t/2
t /3
t

14. Вплив сильної нелінійності на процес коливань

Рівняння коливань
d 2r
m
k (r )r
dt 2
де функція k (r)> Про описує жорсткість пружини, - одне з відносно в
небагатьох нелінеіних рівнянні, для якого можна виписать
спільне рішення. Вводячи величину швидкості
m
dr
v
dt
dv
k (r )r
dt
dr
v
dt
Ділячи перше з цих рівнянні на друге, отримаємо нелінейне рівняння
першого порядку
dv
k (r )r
m
dr
v
Поділяючи в змінні і двічі інтегруючи останнє рівняння, знаходимо
r
dr 2
v ( ) 2 k ' (r ' )r ' dr ' C
0
dt
2
r
dr
C 2 k ' (r ' )r ' dr '
0
dt
k (r )
k (r )
m
'
r
r
0
0
1
t dr ( C 2 k ' (r ' )r ' dr ' ) C1

15. Дякую за увагу

Презентацію підготувала :
Гончаренко Анастасія
БМР 1-15