Similar presentations:
Перестановки, размещения, сочетания
1.
Тема урока:2.
Факториал .Произведение n натуральных чисел от
1 до n обозначают n!
1 2 3 ... (n 1) n n!
Например :
2! 2 1 2
3! 3 2 1 6
1! 1 и 0! 1
3.
1.Перестановки .Перестановка из n элементов – это
расположение их в определенном порядке.
Для любого натурального числа n
справедлива формула
Pn n!
4.
Антон, Борис и Виктор купили3 билета на футбол на 1-е, 2-е, 3-е
места первого ряда стадиона.
Сколькими способами мальчики
могут занять эти места?
© Богомолова ОМ, учитель математики МОУ СОШ № 6 г.Шарьи
4
5.
А (Антон)Б (Борис)
В
(Виктор)
1-е место
А
А
Б
Б
В
В
2-е место
Б
В
А
В
А
Б
3-е место
В
Б
В
А
Б
А
P3 = 3!
5
6.
7.
x1 , x2 , x3Назовите все пары элементов, составленные
из них:
Размещением из n элементов
x1 , x2 , x3 ,..., xn по k называют
любой упорядоченный набор
из k элементов, составленный из
n элементов.
k
n
A
8.
Размещение .A n
1
n
A n(n 1)
2
n
A 3 2 6
2
3
A n(n 1)( n 2) ... (n k 1)
k
n
9.
Пример :Сколькими способами можно распределить
два билета на разные кинофильмы между
семью друзьями?
A 7 (7 1) 7 6 42
2
7
10. 3.Сочетания
Сочетанием из n элементов по k называют любуюгруппу из k элементов, составленную из данных n
элементов.
Число сочетаний из n элементов по k обозначают
через
(по первой букве французского слова combination –
сочетание).
Разница заключается в том, что если в
размещении переставить местами элементы, то
получится другое размещение, но сочетание не
зависит от порядка входящих в него элементов.
11. Сочетания
12. Пример 2. Сколькими различными способами из семи участников математического кружка можно составить команду из двух человек для
5! 6 7 6 77!
7!
C
21
2!(7 2)! 2! 5! 1 2 5!
2
2
7
13. Пример 3. Из перетасованной колоды, состоящей из 36 карт, наугад взяты 4 карты. Какова вероятность того, что все взятые карты
36!36!
C
4!(36 4)! 4! 32!
4
36
32! 33 34 35 36
58905
32! 1 2 3 4










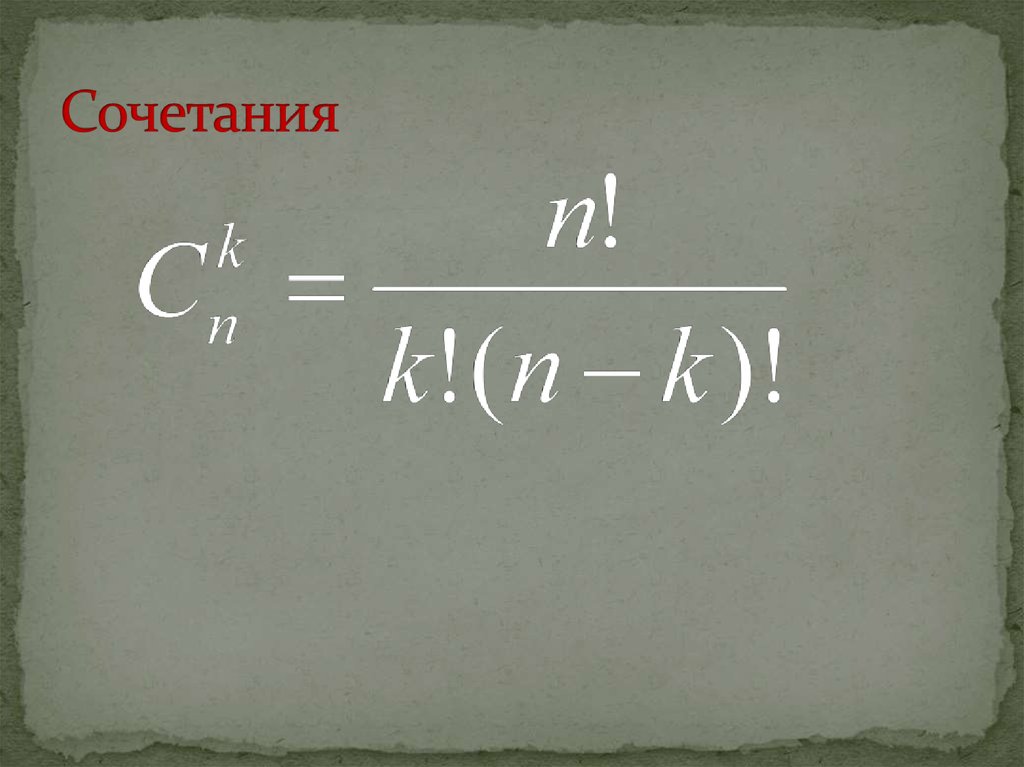


 mathematics
mathematics








